Rep:Mod:mjb216

Ammonia

Ammonia Molecule

NH₃

Bond Length (N-H)	1.01798 Å
Bond Angle (H-N-H)	105.741 (degrees)
Calculation Method	RB3LYP
Basis Set	6-31G(d.p)
Final Energy - E(RB3LYP)	-56.55776873 au
RMS Gradient	0.00000485 au
Point Group	C3v

The experimental bond length of Ammonia is 1.012 Å. This is very similar to the value generated from the computational calculations.

Item Table

         Item               Value     Threshold  Converged?
 Maximum Force            0.000004     0.000450     YES
 RMS     Force            0.000004     0.000300     YES
 Maximum Displacement     0.000072     0.001800     YES
 RMS     Displacement     0.000035     0.001200     YES
 Predicted change in Energy = -5.986271D-10

The optimisation file is liked to here

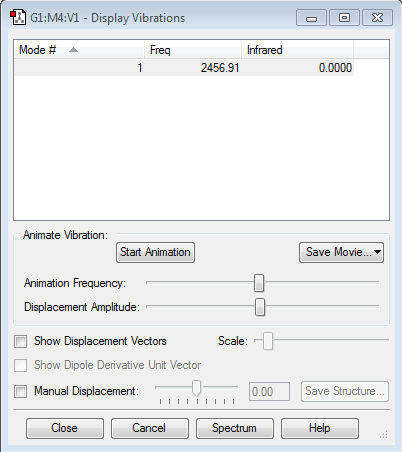
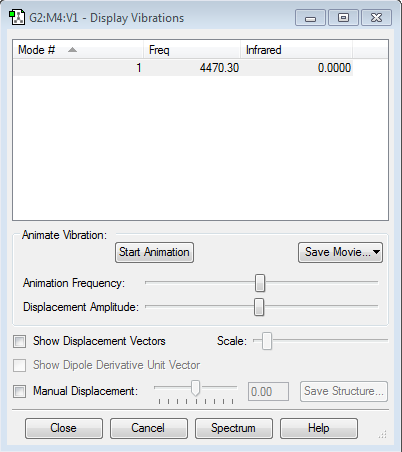
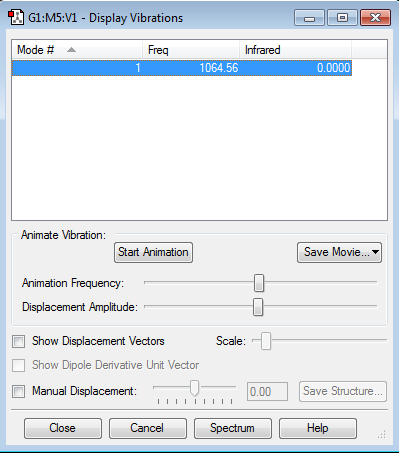
Frequency Analysis

Using the 3N-6 rule, you would expect 6 vibrational modes. Modes 2 & 3 are degenerate and modes 5 & 6 are also degenerate. Modes 1, 2 & 3 are bending. Modes 4, 5 & 6 are stretching. Modes 4 is highly symmetric. Modes 1 is known as the 'umbrella' mode. In an experimental IR spectrum of gaseous ammonia 2 peaks would be present. This can be seen from the intensities of the vibrations, the first mode is very intense, modes 2 & 3 are degenerate, with a reasonable intensity.

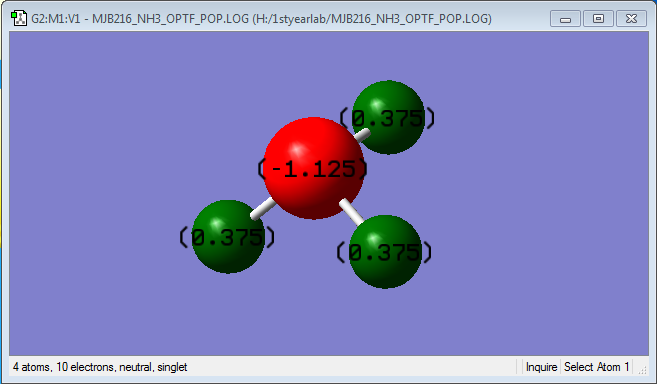
Charge Distribution

As Nitrogen is a more electronegative atom than Hydrogen, it would be expect that the nitrogen atom would withdraw some electron density from the N-H bonds towards it, hence giving it a negative charge.

Nitrogen

Nitrogen Molecule

N₂

Bond Length	1.10555 Å
Calculation Method	RB3LYP
Basis Set	6-31G(d.p)
Final Energy	-109.52412867 au
RMS Gradient	0.00008380 au
Point Group	D∞h

Item Table

         Item               Value     Threshold  Converged?
 Maximum Force            0.000145     0.000450     YES
 RMS     Force            0.000145     0.000300     YES
 Maximum Displacement     0.000045     0.001800     YES
 RMS     Displacement     0.000064     0.001200     YES
 Predicted change in Energy = -6.585141D-09

The optimisation file can be found here

Frequency Analysis

The fact that there are no negative energies shows that the molecule has been fully optimised.

Hydrogen

Hydrogen

H₂

Bond Length	0.74247 Å
Calculation Method	RB3LYP
Basis Set	6-31G(d.p)
Final Energy	-1.17853929 au
RMS Gradient	0.00013423 au
Point Group	D∞h

Item Table

         Item               Value     Threshold  Converged?
 Maximum Force            0.000232     0.000450     YES
 RMS     Force            0.000232     0.000300     YES
 Maximum Displacement     0.000305     0.001800     YES
 RMS     Displacement     0.000431     0.001200     YES
 Predicted change in Energy = -7.091616D-08

The optimisation file can be found here

Frequency Analysis

The fact that there are no negative frequencies show that the molecule has been fully optimised.

Haber–Bosch process

N₂ + 3H₂ -> 2NH₃

E(NH3)	-56.55776873 au
2*E(NH3)	-113.11553746 au
E(N2)	-109.52412867 au
E(H2)	-1.17853929 au
3*E(H2)	-3.53561787 au
ΔE = 2*E(NH3) - [E(N2) + 3*E(H2)]	-0.05579092 au		-146.479071618 KJ/mol		-146.48 KJ/mol (2.dp)

The Ammonia product is more stable as it has a very exothermic formation energy indicating that it is lower in energy than the reactants. The formation enthalpy of Ammonia is -10.93kcal., which equates to 45.76 KJ/mol. As we have formed 2 moles of NH₃ in this reaction the ΔE = 91.52 KJ/mol. There is quite a large difference between the literature value and the value from the optimisation. This is because the computer calculates the energies at 0K, whereas the formation enthalpy is measured at 298K. This would cause the difference seen.

Fluorine

Fluorine Molecule

F₂

Bond Length	1.40298 Å
Calculation Method	RB3LYP
Basis Set	6-31G(d.p)
Final Energy	-199.49825220 au
RMS Gradient	0.00000046 au
Point Group	D∞h

Item Table

         Item               Value     Threshold  Converged?
 Maximum Force            0.000001     0.000450     YES
 RMS     Force            0.000001     0.000300     YES
 Maximum Displacement     0.000001     0.001800     YES
 RMS     Displacement     0.000001     0.001200     YES
 Predicted change in Energy = -7.876732D-13

The optimisation file can be found here

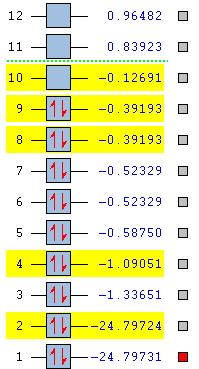
Frequency Analysis

The fact that there are no negative frequencies shows that the molecule is fully optimised. As Flourine has no dipole moment, it will have no intensity in the IR spectrum.

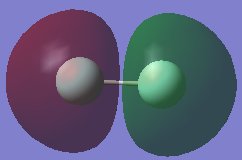
Charge Density

The picture above clearly shows that there is no difference in charge on the two Fluorine atoms. This is because both atoms are the same (Fluorine), and so the electrons will be experiencing the same effective nuclear charge from both, and hence have equal attraction between them. Another way of looking at it is that both atoms have the same electronegativity (as they are the same atom) and so neither will attract electron density more.

Molecular Orbitals Of Fluorine

This shows the different energy levels involved in the molecular orbitals. The ones highlighted in yellow represent the antibonding orbitals.

This shows the 1s orbitals for fluorine. They are barely visible which shows that they are extremely contracted due to the high nuclear charge they are experiencing, making them very deep in energy as shown by the first level in the table. They are core orbitals, meaning there is no interaction between them (or very little).

This is the 2σg bonding orbital.It is gerade (g) as the phase stays the same after undergoing inversion symmetry with the middle of the bond corresponding to the centre of inversion. It corresponds to number 3 on the list. It corresponds to number 6 on the list. The atomic orbitals contributing are the 2s orbitals from each Fluorine atom. There is significant overlap between the two atoms, however due to the σ*u

This is the 2σ*u molecular orbital. It is ungerade (u) symmetry due the phase changing after undergoing inversion symmetry. It corresponds to number 4 on the list. The 2s atomic orbitals are out of phase, which results in a nodal plane being formed between the two atoms. This is a region of no electron density, meaning the bond will not form. This 2σ*u orbital cancels out the bonding effects of the 2σg bonding orbital.

This is the 3σg orbital. It has gerade symmetry. It corresponds to number 5 on the list. There is quite significant overlap between the two atoms, and orbital represents the σ bond in Fluorine as the corresponding σ* orbital is not filled. The atomic orbitals involved are the 2pz orbitals on both Fluorine atoms.

This is the 1πu molecular orbital. It has ungerade symmetry. It corresponds to number 6 on the list. There is overlap above and below the plane, however, it is not as significant as in the σ orbitals, hence it is higher in energy the 3σg orbital. The 2px atomic orbitals on Fluorine contribute to this molecular orbital There is another degenerate orbital which is from the 2py interaction.

This represents the 1π*g molecular orbital. It has gerade symmetry. It corresponds to number 8 on the list. There is a nodal plane in the middle of where the bond should be which shows its antibonding. This counteracts the bonding effects of the 1πu orbital. The atomic orbitals involved are the 2px orbitals from Fluorine. There is another degenerate antibonding orbital which is from the 2py. They represent the HOMO.

This is the 3σ*u orbital. It has ungerade symmetry. It corresponds to 10 on the list. There are 3 nodal planes, and due to the different phases in between the two atoms there is destructive interference. It is unoccupied in this molecule, and represents the LUMO.

Methanal (Formaldehyde)

Formaldehyde

CH₂O

Bond Length (C=O)	1.20661 Å
Bond Length (C-H)	1.11054 Å
Bond Angle (H-C-H)	115.204 (degrees)
Bond Angle (O-C-H)	122.400 (degrees)
Calculation Method	RB3LYP
Basis Set	6-31G(d.p)
Final Energy	-114.50319935 au
RMS Gradient	0.00004448 au
Dipole Moment	2.1823 (debye)
Point Group	C2v

The experimental bond length of F₂ is 1.41 Å.. This is very similar to the computational value calculated.

Item Table

         Item               Value     Threshold  Converged?
 Maximum Force            0.000052     0.000450     YES
 RMS     Force            0.000034     0.000300     YES
 Maximum Displacement     0.000142     0.001800     YES
 RMS     Displacement     0.000092     0.001200     YES
 Predicted change in Energy = -1.371199D-08

The optimisation file can be found here

Charge Distribution

The charge distribution shows that the oxygen has withdraw electron density from the molecule onto itself, giving it a slight negative charge represented by the red colour in the picture. The carbon is slightly positive due to a lack of electron density around it. The blue arrow shows the dipole moment.

Molecular Orbitals

HOMO

LUMO

This shows the HOMO & LUMO of the C=O bond. The antibonding region over the Carbon is much larger than that on oxygen. This would explain why during nucleophilic attack of the carbonyl group, the nucleophile always attacks the carbon atom and not the oxygen. The reason that the antibonding orbital is bigger is due to Carbon's atomic orbitals being higher in energy than oxygen's, due to the orbitals being less contracted (experience a lower effective nuclear charge). As Carbon's orbitals are higher in energy, they contribute more to the antibonding orbitals, hence why the π* lobe is much larger on carbon as highlighted in the LUMO diagram.