Rep:Mod:mj506 mod3

Cyclohexadiene tutorial

The anti conformation of the molecule was optimized using Gaussian software using HF method with 3-21G basis set. Energy obtained was -231.68907064 a.u. Point group was C1, but after clicking on symmetrize, the point group became C_2h.
Structure was redrawn in gauche conformation, and again optimized using the same method/basis set as above. Energy obtained was -231.68771615 a.u. Point group was C1,and after symmetrizing it became C2. One would expect the energy of this conformation to be higher, as gauche conformation takes away the stabilizing hyperconjugation effect of anti-periplanar conformation, and that's what is found by the calculation.
A structure was drawn where one might expect a hyperconjugation between C-H bonding orbital and C-C antibonding orbital. Conformation was chosen anti, as it is lower in energy. Optimization performed again with HF with 3-21G basis set. But the energy found was the same as for the anti conformation above, and the structure restored to the one obtained above as well. Thus one can conclude that this is the lowest energy state of the molecule.
Comparing my structures with the ones in Appendix 1, the anti conformation I have obtained is anti3 and gauche is gauche1 from the Appendix 1. That is quite embarrasing, as there are lower energy states for these conformations in the appendix, which I have failed to find (anti1 and gauche3).
Structure anti2 was drawn and optimized twice to make sure it obtains the C_i point group. The final energy was -231.69253529 a.u., which compares perfectly with the one from the table at -231.69254 a.u.
The structure was used to re-optimize it using B3LYP method with 6-31G(d) basis set. Point group was again obtained to be C_i. The total energy was -234.61172247 a.u. Bond lengths and bond angles that differ are given in the table below:

Method	C=C bond length	-C-C- bond length	-C-C= bond length	C(sp3)-H bond length	C(sp2)-H bond length	C-C=C bond angle
B3LYP	1.33349 A	1.54794 A	1.50415 A	1.09976 A	1.08852	125.290
HF	1.31614 A	1.55287 A	1.50877 A	1.08477 A	1.07336	124.811

Thus as one can see, the bond lengths and angles differ by a slight amount, most notably the bond lengths are somewhat shorter for the B3LYP method.
Frequencies of vibrations have been performed with the B3LYP method with 6-31G(d) basis set. No negative values for frequencies were obtained, with the lowest lying frequency at 74 cm^-1. The energies obtained under the thermochemistry tab are outlined in the table below:

Sum of electronic and zero-point Energies=           -234.469162
Sum of electronic and thermal Energies=              -234.461827
Sum of electronic and thermal Enthalpies=            -234.460883
Sum of electronic and thermal Free Energies=         -234.500716

Optimizing the chair and boat transition states

Chair transition structure

Allyl fragment was optimized using HF with 3-21G basis set. Then another allyl fragment was added and positioned so it is in the chair-like transition state. Distances between terminal carbons was adjusted to be 2.2A. The optimization and frequency of this structure was performed with the following command line:

# opt=(calcfc,ts,noeigen) freq hf/3-21g geom=connectivity

Calculation finished successfully, and the terminal C-C distance was modified to 2.02A. One imaginary frequency was obtained at 818 cm^-1 and upon animating it, one can see that it corresponds to the Cope rearrangement, as the terminal carbons move as though they are about to create a bond.

The initial unoptimized structure was opened and edited with Redundant Coord Editor, making two of the terminal carbons a bond and freezing coordinates. The structure was then optimized using the following command line:

# opt=modredundant hf/3-21g geom=connectivity

Optimization finished successfully, and the transition state looks very similar to the one obtained above using opt=ts, except the terminal carbon-carbon distances were frozen at 2.2A.
Structure obtained from above was used in the redundant coord editor, to fix the two bonds which are made/broken to derivative, and optimzation of the TS was run with the below command line:

# opt=(ts,modredundant) rhf/3-21g geom=connectivity

Optimization finished successfully, and comparing the structure to one obtained with minimising the TS and calculating the force constants, it is almost exactly the same structure, as the terminal carbon-carbon distances are changed to 2.02A and the imaginary vibration is almost exactly at -818 cm^-1. Structure obtained is given on the right.

Boat transition structure

The HF optimized hexadiene anti-2 conformation was used (with point group C_i). Two molecules of the hexadiene were added, and the atoms numbered so to resemble the reactant and product, as shown below:

The optimization was then run with the following command line:

# opt=qst2 freq hf/3-21g geom=connectivity

And Gaussian crashed straight away. The reactant and product were rearranged so that C2-C3-C4-C5 dihedral angle was 0 degrees, and C3-C4-C5 and C2-C3-C4 were 100^o degrees both. Hydrogen atoms were also renumbered so no confusion will be involved, and the final molecule is shown below:

The optimization was then run with command line:

# opt=qst2 freq hf/3-21g geom=connectivity

Gaussian finished without any error. The structure obtained is indeed the boat transition structure, with the terminal carbon-carbon distance being 2.14A, and the only imaginary frequency at -839 cm^-1. Below is the the boat conformation of transition state:

It is not really possible to predict which conformer given in Appendix 1 will be formed from the boat/chair transition states. Thus, the IRC method had to be used to predict to which reactant conformation does the molecule drop to from the chair transition state, which is detailed below.

Intrinsic reaction coordinate method

The optimized chair transition state was opened, and a Gaussian file prepared by choosing the method of calculation as IRC, following IRC only to the forward reaction, force constants were chosen to be calculated once, and points to compute was changed to 50. THe overall command line looks like:

# irc=(forward,maxpoints=50,calcfc) rhf/3-21g geom=connectivity

The job was submitted to chemistry SCAN. After an hour, the calculation was finished successfully. Checkpoint file was opened, and the reaction path animated, showing the bond making in 51 steps. Unfortunately, that was not enough to obtain the final structure, and so further optimization was required. The terminal carbon atoms came close together to be in a bond length distance at around 43rd iteration.
The final (51st) structure was further minimized using HF method with 3-21G basis set. A gauche2 structure was obtained with C2 point group. Thus, the conformation to which the molecule falls from chair transition state (and which is predicted by HF method with 3-21G basis set) is gauche2. The final reactant structure was also attempted to be obtained with using IRC method and setting to always calculate the force constants, unfortunately the Gaussian job crashed after 15 steps and was the job was abandoned due to time constraints. So for the final structure, a gauche2 optimized structure was chosen.

Activation energies of the Cope rearrangement

The Cope rearrangement can proceed through boat or chair conformation. Transition states of both chair and boat conformations have been optimized using B3LYP method with 6-31G(d) basis set, with the following command line:

# opt=(calcfc,ts,noeigen) freq rb3lyp/6-31g(d) geom=connectivity

Table below summarizes energy values obtained from the calculations:

Structure	Electronic energy with HF/3-21G	Electronic + zero-point energy with HF/3-21G at 0K	Electronic + thermal energies with HF/3-21G at 298K	Electronic energy with B3LYP/6-31G(d)	Electronic + zero-point energy with B3LYP/6-31G(d) at 0K	Electronic + thermal energies with B3LYP/6-31G(d) at 298K
Anti2 reactant	-231.69253529 a.u.	-231.539540 a.u.	-231.532566 a.u.	-234.61171866 a.u.	-234.469162 a.u.	-234.461827 a.u.
Gauche2 reactant	-231.69166792 a.u.	-231.538705 a.u.	-231.531794 a.u.	-234.61068821 a.u.	-234.468261 a.u.	-234.460957
Chair TS	-231.61932244 a.u.	-231.466697 a.u.	-231.461338 a.u.	-234.55698303 a.u.	-234.414930 a.u.	-234.409009
Boat TS	-231.60280229 a.u.	-231.450929 a.u.	-231.445300 a.u.	-234.54309304 a.u.	-234.402340 a.u.	-234.396006 a.u.

Activation energies in a.u. and kcal/mol are given in the table below. Energies for both methods were taken from the frequency calculation from Thermochemistry section, namely the "Sum of electronic and zero-point Energies" which is at 0 K.

Structure	Energy with HF	Energy with B3LYP	Activation energy with HF	Activation energy with B3LYP
Product gauche2 conformation	-231.538705 a.u.	-234.468261 a.u.	---	---
Chair transition state	-231.466697 a.u.	-234.414930 a.u.	0.072008 a.u. = 45.2 kcal/mol	0.053331 a.u. = 33.5 kcal/mol
Boat transition state	-231.450929 a.u.	-234.402340 a.u.	0.087776 a.u. = 55.1 kcal/mol	0.065921 a.u. = 41.4 kcal/mol

As one can see from the above values obtained from B3LYP method, they compare extraordinarily well with the ones obtained experimentally, namely 33.5 and 44.7 kcal/mol values at 0K. Also, one can see that the B3LYP method gives much better values than the HF method. One can obtain the activation energy at 298K using the values with thermal corrections from the table above, but as no experimental values are given, there is no need to do so.

Diels-Alder cycloaddition

Cis-butadiene HOMO and LUMO

Cis-butadiene was drawn in GaussView and optimized using AM1 semi-empirical method with the command line:

# opt am1 geom=connectivity

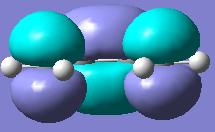
Checkpoint file was opened and MO's visualized. The HOMO and LUMO orbitals are given below, along with their assigned symmetries:

HOMO orbital, a symmetry with respect to plane	LUMO orbital, s symmetry with respect to plane

Transition state of Diels-Alder of butadiene and ethene

Transition state structure of the Diels-Alder reaction of cis-butadiene + ethene has been drawn using GaussView. First, a bicyclo structure was drawn as suggested, then CH2CH2 fragment was disconnected, and bond distances of the terminal butadiene carbons and alkene carbons increased to 2.2A. After transition state optimization with the following command line:

# opt=(calcfc,ts,noeigen) freq am1 geom=connectivity

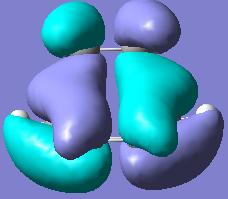
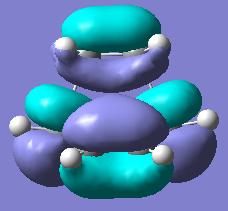
The optimized structure was obtained, where the 2.2A distance between partly formed C-C bonds was modified to 2.1A. The MO diagrams of the HOMO and LUMO of the structure were obtained and are shown in the table below (along with symmetry with regards to the plane):

HOMO orbital of TS, symmetry a	LUMO orbital of TS, symmetry s	Picture of the TS

As one can see, the HOMO of the structure is a mixture of LUMO of alkene and the HOMO of diene which are in-phase, that is have the same symmetry and thus is allowed. While the LUMO of the TS is the mixture of HOMO of alkene and the LUMO of butadiene.

The typical sp³ carbon-carbon bond length is in the order of 1.5A, while a sp² carbon-carbon bond is around 1.33A. The typical van der Waals radius of a carbon atom is 1.70A. As the van der Waals radius of an atom can have several definitions and so a few values, it can vary between 1.7A to 1.9A. As the partly formed C-C bond is of 2.1A, one can assume there is no bond character at this distance.

The vibration which corresponds to the synchronous bond making is at -955 cm^-1, and indeed corresponds to a Diels-Alder product formation. The vibration is attempted to visualize below:

TS at rest, C-C distance 2.1A	Vibration at its furthest point, C-C distance 1.6A

The next lowest positive vibration is one at which the molecules are rotating with respect to each other, in opposite directions.

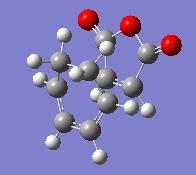
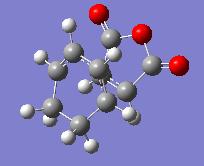
Transition states of maleic anhydride and cyclohexadiene Diels-Alder reaction

Exo and endo transition structures have been drawn of the exo and endo products of the maleic anhydride and cyclohexadiene Diels-Alder reaction. The initial partly formed C-C distances were set to 2.2A and also 1.9A, but both ways the structures were optimized to the same Transition State structures shown below. They were optimized using AM1 semi-empirical method, with the command line:

# opt=(calcfc,ts,noeigen) freq am1 geom=connectivity

The resulting structures and their energies are given in the table below:

	Exo transition state	Endo transition state

Energy	-0.05050325 a.u.	-0.05159429 a.u.
C-C partly formed	2.17A	2.16A
C-C of the bridge	1.52207 A	1.52293 A
C=C of maleic anhydride	1.410A	1.408A
C=C of cyclohexadiene	1.39677 A	1.39723A
C-C through space of CO-O-CO and C of cyclohexadiene	2.9447 A	2.8925 A

One can see that the endo transition state is lower in energy than the exo transition state, thus proving that the Diels-Alder reaction gives only endo product as it is the kinetic product. The difference is 0.68kcal/mol. The difference is so small most probably due to the inaccuracy of the method used - it is semi-empirical, thus not very reliable. The embarrasing and annoying bit is that the C-C through space distance of CO-O-CO fragment and C on cyclohexadiene in the endo form is almost the same as for the exo form. One would expect orbital interactions to decrease the distance of the endo structure, but that is not observed. That is further investigated in the HOMO analysis below. All the other bond distances are fairly similar of both endo and exo TS.

The exo could be more strained due to two reasons: one steric, one secondary orbital effect. Steric effect is due to some van der Waals repulsion between hydrogens on sp3 carbons on cyclohexadiene which are in proximity of the CO-O-CO fragment, and thus pushing it away. The secondary orbital effect is missing from the exo isomer, but is present in the endo, and that is explained in more detail in the section about HOMO below.

The HOMO of both exo and endo TS structures have been obtained and are shown in the following table:

HOMO of TS of exo	HOMO of TS of endo

As one can see from the HOMO diagrams above, the p orbitals on carbons of the fragment CO-O-CO are also participating. These orbitals overlap with the alkene LUMO of the maleic anhydride, and then that MO is participating in the Diels-Alder reaction. The HOMO of both endo and exo is thus made up of the HOMO of diene and LUMO of the maleic anhydride, and the LUMO of maleic anhydride has contribution from the CO-O-CO fragment. When the transition state is endo, the p orbitals of carbons on CO-O-CO can overlap heads on with the diene HOMO orbital - which are the secondary orbital overlap interactions. But that unfortunately is not seen in the endo HOMO above. Both HOMO orbitals have a symmetry with respect to the plane of symmetry, but the participating HOMO and LUMO orbitals are in-phase with each other and thus the bond forming is allowed.

One has to note that all the calculations (except where indicated) have been done with the semi-empirical AM1 method, which does not solve the Schrodinger equation and is not quantum mechanical. That really limits the accuracy of the calculations, and some secondary orbital overlap effects which might be expected to be there, are not observed due to that. Thus, a lot of small quantum mechanical factors have been ignored in the optimizations of the transition states of the Diels-Alder reaction.

In addition to the above calculations, a B3LYP with 6-31G(d) basis set optimization of the transition state was run on the endo compound, but to disappointment, the secondary orbital overlap effects were not clearly observed in the HOMO of the molecule, which looks like that:

The geometry obtained with B3LYP did not differ from the AM1, except the C-C bond lengths were slightly increased, and the partly formed C-C single bonds were increased to 2.26A from 2.16A.