Rep:Mod:mj506 mod2

BCl₃ introduction module

A molecule of BCl₃ was optimized using Gaussian software. The method and basis set used were B3LYP/3-21G. The optimized B-Cl bond distance was calculated to be 1.77503 A, and the Cl-B-Cl angle was exactly 120.000^o.
The calculation output included the following information: File type: .log, Calculation type: FOPT, Calculation method: RB3LYP, Basis set: 3-21G, Final energy: -1398.8 a.u., Dipole moment: 0 Debye, Point group: D_3H, Calculation took 22 seconds.

COCl₂ optimization

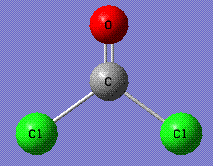
A molecule of COCl₂ was optimized using Gaussian software (calculation time: 37.0 seconds). Calculation method was RB3LYP with 3-21G basis set. The xyz coordinates of the optimized molecule http://hdl.handle.net/10042/to-1178:

---------------------------------------------------------------------
Center     Atomic     Atomic              Coordinates (Angstroms)
Number     Number      Type              X           Y           Z
---------------------------------------------------------------------
   1          6             0        0.000000    0.576144    0.000000
   2          8             0       -0.000087    1.760776    0.000000
   3         17             0       -1.510797   -0.516082    0.000000
   4         17             0        1.510838   -0.515863    0.000000
---------------------------------------------------------------------

The C-Cl bond distance is 1.86426 A, and the C=O bond distance is 1.18463 A.
The Cl-C-Cl bond angle is 108.3^o, and the Cl-C=O bond angle is 125.9^o.
The final energy of the molecule is -1028.7 a.u.
The dipole moment is 0.2681 Debye.
The point group (according to Gaussian output) is C_S, but that is incorrect, as the actual point group of COCl₂ is C_2v.

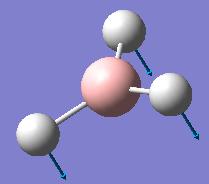
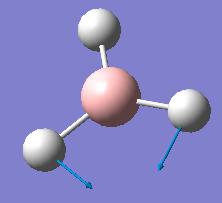
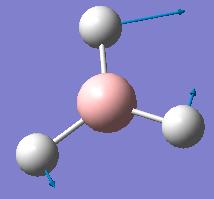
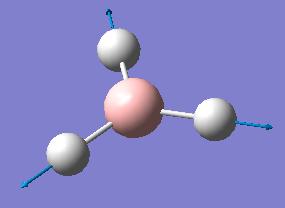
BH₃ vibrations

Vibrational frequencies of the optimized BH₃ molecule were obtained using B3LYP method with 3-21G basis set. Vibrations are summarized in the table below.

**Frequency/vibrational analysis of BH₃**
- No.-	- Form of the vibration -	- Frequency / cm^-1 -	- Intensity -	- Symmetry label D_3H point group -
1	All H atoms moving in and out of the plane of the molecule	1146.03	92.6653	A₂''
2	Bending motion of two H atoms, while one H atom is kept stationary	1204.86	12.3919	E'
3	All hydrogen atoms moving in bending motion, in plane of the molecule	1204.86	12.3944	E'
4	All hydrogen atoms stretching symmetrically	2591.65	0	A₁'
5	Two hydrogen atoms stretching anti-symmetrically, one H atom stationary	2730.07	103.857	E'
6	Two H atoms stretching symmetrically away from B, and one stretching towards B	2730.07	103.85	E'

The Infrared spectrum, as predicted with Gaussian software, is given below. It must be noted that although we see 6 vibrations in the table above, there are only 3 peaks in the spectrum below. It is due to two pairs of the vibrations being degenerate, thus resulting in peaks occuring at same frequencies, and one vibration, the number #4 one, is totally symmetric and that vibration does not change the dipole moment of the molecule, a selection rule for the peak to appear in the infrared spectrum. All the other vibrations do change the dipole moment of the molecule and thus appear in the IR.

Molecular Orbitals of BH₃

Molecular orbitals were obtained from BH₃ molecule using B3LYP method with 3-21G basis set. Bond angles were manually set in the .gjf file to be equal to 120^o so the correct point group is obtained - D_3H. MO's as drawn by qualitative MO approach and the corresponding calculated MOs are shown below.

**MO diagrams of BH₃**
Symmetry of MO	MO obtained with B3LYP	MO obtained with qualitative method
a₁'
a₁'
e'
e'
a₂

As can be seen from the diagrams above, there are no significant differences between the MOs obtained by qualitative MO approach and by quantitative, except for the size of the orbitals. Obviously, as no quantification is used in the qualitative MO approach, only intuition can be used to guess the size of the orbitals, but for the software approach, exhaustive mathematical methods are used to obtain the sizes as exact as possible. This shows that for basic purposes, qualitative MO approach is very powerful technique, as it does not involve any elaborate calculations, but just simple symmetry considerations and yields relatively accurate bonding picture of the molecule in question.

Isomers of Mo(CO)₄(P(CH₃)₃)₂

Geometric parameters and optimization of trans and cis compounds

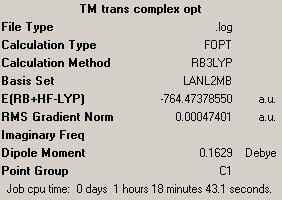
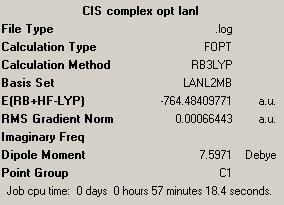
Gaussian output for trans compound (LANL2MB)

Gaussian output for cis compound (LANL2MB)

Molecules of trans and cis Mo(CO)₄(P(CH₃)₃)₂ were drawn in ChemBio3D and optimized using MM2 method. It was then saved as .gjf files and optimized first using B3LYP method with LANL2MB basis set and parameter opt=loose. The summary output can be seen in the boxes on the right. Then the optimized structure was taken and optimized further using B3LYP method with LANL2DZ basis set, using additional keywords int=ultrafine and conver=scp=9. These were uploaded on the digital repository, trans complex and cis complex.

Trans complex http://hdl.handle.net/10042/to-1187

Cis complex http://hdl.handle.net/10042/to-1188

Trans complex

Cis complex

Literature values of trans and cis Molybdenum tetracarbonyl bis(triphenylphosphine) bond distances were found^[1] and are outlined in the table below, along with the computational values.

Geometric values of cis and trans Molybdenum compounds
Compound	Mo-P bond length	P-Mo-P angle	Mo-C bond length	C-Mo-C angle	C=O bond distance
Cis	2.648 A	42.4^o	2.032 A and 1.983 A	88^o and 90^o	1.188 A and 1.191 A
Cis lit.	2.654 A	N/A	N/A	N/A	N/A
Trans	2.572 A	177^o	2.030 A	88.9 ^o	1.191 A
Trans lit.	2.544 A	N/A	2.020 A	92.17^o	N/A

The computational values agree with experimental ones pretty impressively well, and one could attribute the difference in Mo-P bonds due to methyl groups used in calculation instead of phenyl ones. Other than that, the bond lengths agree very well, and that again shows that the calculation did not go wrong.

Vibrational frequencies of the trans and cis compounds

The vibrational frequencies were calculated using B3LYP method with LANL2-DZ basis set. Experimental values for trans^[2] and cis^[3] compounds. The calculated and experimental values are compared in the table below.

**C=O vibrations in cis and trans compounds**
Compound	Frequency	Intensity	Frequency from lit.
Cis	1848	1069	1860
http://hdl.handle.net/10042/to-1194	1850	1961	1880
	1869	665	1891
	1960	321	2013
Trans	1837	1999	1891
http://hdl.handle.net/10042/to-1195	1837	1997	1891
	1881	6.7	none
	1953	2.9	none

The differences between the computed and experimentally observed vibrational frequencies arise due to different substituents at phosphorus (in calculation methyl groups were used, while experimentally it was phenyls). Other than that, values agree pretty well. Cis shows more absorptions in the IR due to lower symmetry of the molecule, being C_2v, and so symmetric stretches are also visible in the IR spectrum. While trans complex is D_4h and the symmetric stretches do not change the dipole moment and thus are not visible in the IR. If Gaussian had determined the correct point group in the first place, vibrations at 1881 and 1953 cm^-1 would have been with 0 intensity.
Vibrations in the trans compound are slightly lower in frequency than for the cis compound.

General comparison of cis and trans

The energy obtained (with LANL2-DZ basis set) in atomic units for trans compound was -773.35737509, and for cis was -773.36024020. Thus the difference between them is E(cis)-E(trans)= -0.00286511 Hartrees = -7.520 kJ/mol. That means the cis compound is more stable, which is sort of counter intuitive, as one would expect the cis compound to be more sterically strained.
The cis compound is stabler due to some sort of trans effect, as both C=O pi* orbital and phosphorus d orbitals are competing for Molybdenum d electrons. When the compound is trans, the two pairs of C=O compete for the same d electrons, and C=O is a better acceptor of the d electrons than the Phosphorus ligand. Hence, when phosphorus are aligned trans, C=O gets less Molybdenum d electrons and phosphorus gets more, thus the stabilisation energy is lower and the cis isomer is preferred. In order to stabilise the trans isomer, one would add strong electron withdrawing ligands to phosphorus (e.g. CN, F), and in order to stabilise the cis isomer, one would add strong electron donating ligands to phosphorus (e.g. OH, NH₂).

Investigation of Ammonia molecule

Geometry optimization of Ammonia molecule

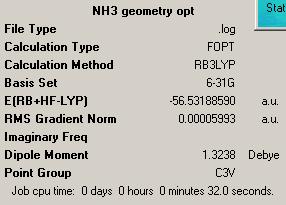
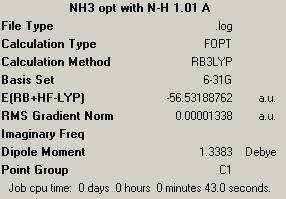
Summary of NH₃ optimization with N-H bond length increased

The geometry was optimized of the ammonia NH₃ molecule using B3LYP method with 6-31G basis set. The summary of the calculation output is given on the right. Point group obtained was C_3v, just as one would expect. Then the bond length of initial NH₃ molecule of one N-H bond was increased to 1.01 A (others were set at 1.00 A) and optimization was run again, with B3LYP method with 6-31G basis set. The summary is shown on the right. And finally, geometry optimization was run on a planar NH₃ molecule to obtain the D_3h symmetry. Summary is also provided on the right.

The symmetry, which was defined initially by setting atomic positions to pre-defined values, confuses Gaussian at it fails to obtain the correct symmetry. That was observed on the molecule in which one N-H bond was made 0.01 A longer. In that optimization, Gaussian obtained C1 symmetry and the N-H bond was 0.00001A shorter than the other two. While for the other molecules, which were defined with correct symmetry in the initial input file, the geometries obtained are as one would expect: with the same N-H bond lengths, bond angles. The D_3h obtained is planar.

For the Highest symmetry D_3h, the calculation time was 1min 18s, for C1 it was 43s and for C_3v it was 32s, thus the initial symmetry does make a difference to the calculation time.

The molecule cannot break symmetry during an optimisation, and thus if you enter a high symmetry molecule to optimise, you have to make sure you enter it with the correct symmetry initially, as Gaussian will make sure the optimisation is made on the symmetry initially provided.

The lowest energy geometry of these three optimisations was obtained for the C1 symmetry.
The C_3v isomer is higher in energy by 1.72 * 10^-6 a.u. = 4.51 J/mol.
The D_3h isomer is higher in energy by 3.46 * 10^-4 a.u. = 907.4 J/mol.
The energy difference between these isomers is not significant and is pretty small, as the room temperature (298K) would give 2477 J/mol, which is more than sufficient to populate all three symmetries in significant proportions (using Boltzmann distribution).

Using higher level calculation

Geometry was optimised for C_3v molecule using MP2 method with 6-311G(d,p) basis set. The calculation took 33s, which is just 1s more than for the B3LYP with 6-31G basis set. The NH₃ molecule with D_3h symmetry was also optimized using MP2 with 6-311G(d,p) basis set, and the calculation took 1min 40s, which is 22s longer than the corresponding calculation using B3LYP with 6-31G basis set.
Energy difference between the C_3v and D_3h symmetries was calculated to be 7.796 * 10^-3 a.u. = 20.47 kJ/mol, which is an increase from 0.903 kJ/mol for the B3LYP calculation! That is indeed a huge difference - an increase by 2100%. And this new value compares very well with the experimental value of 24.3 kJ/mol, although not perfect.

Vibrations of NH₃

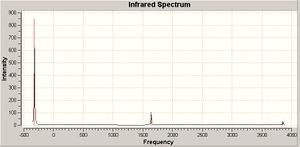
Vibrational spectrum of the optimized NH₃ molecule with D_3h and C_3v were calculated using the B3LYP method with 6-31G basis set. The frequencies are given in a table below.

**Frequencies and intensities of D_3h and C_3v symmetric NH₃ molecule**
Symmetry	Frequency	Intensity
D_3h	-318	849
	1640.59	55.9828
	1640.59	55.9805
	3635.71	0
	3854.27	19.5951
	3854.27	19.5963
C_3v	452.3	599.5
	1680.47	41.7256
	1680.47	41.7245
	3575.43	0.0688
	3775.76	7.0892
	3775.76	7.0884

Vibrations for C_3v, the 1680 and 3775 vibrations have the E symmetry label, the 452 vibration and the 3575 one have A₁ symmetry label. There are five positive vibrations for the D_3h symmetric ammonia and six positive vibrations for the C_3v symmetric ammonia. Comparing the actual vibration modes of motion, one can see that the vibrations match visually with the order in which they are written down above in the frequency table. That makes perfect sense, as the point group C_3v is a subgroup of D_3h, and thus the same vibrational motions are observed, but energies for them differ.
The IR spectra for C_3v can be compared to one obtained experimentally
The negative frequency in D_3h at -318 cm^-1 is the one that follows the inversion path. It has a negative value due to the way Gaussian calculates the IR spectra: it is more energetically favourable for it to be in the excited vibrational state, as it is then in the C_3v symmetric state, and so energetically more favourable. The symmetry label for it is A₂''

Investigation of TiX₄

Aims and objectives of the experiment

Compounds of titanium tetrahalogenates have been chosen as the subject of this mini-project. These compounds will be investigated in terms of their geometry, energy, bonding, vibrational frequencies and some other aspects, namely why TiCl₄ is a liquid while TiF₄ is a solid at room temperature.

Energies of formation and geometries of TiX₄

Geometries of TiX₄, here X = F, Cl, Br and I were optimized using B3LYP method with LANL2DZ basis set. All the geometries observed were tetrahedral and thus the point group is T_d for all four compounds. In order to calculate and compare energies of formation, energies of X₂ have also been calculated using the same basis set.

Molecule	Energy in a.u.	Calculation
Ti singlet	-57.90831089	LANL2DZ
Ti triplet	-57.96110151	LANL2DZ
F₂	-199.54456711	LANL2DZ
Cl₂	-29.84319939	LANL2DZ
Br₂	-26.30904851	LANL2DZ
I₂	-22.76939316	LANL2DZ

Energies obtained above were used to calculate the energies of formation of TiX₄. These were obtained by optimizing the TiX₄ structures using B3LYP with LANL2DZ basis set, and using the energy to obtain the difference in energy upon TiX₄ formation. Namely, dE_formation = E(TiX₄4) - E(Ti) - 2E(X₂). Triplet state of titanium was used, as it is lower in energy.

Molecule	Energy of molecule in a.u.	Energy of Ti + 2X₂	dE_formation in a.u.	dE_formation in kJ/mol
TiF₄	-457.81688363	-456.9974451	-0.81943851	-2151.4
TiCl₄	-118.12849433	-117.5947097	-0.53378463	-1401
TiBr₄	-110.97655098	-110.5264079	-0.45014299	-1182
TiI₄	-103.82494445	-103.4470972	-0.37784719	-992

The energy of formation values might not be exactly correct, but the trend is definitely as one would expect it to be. Fluorine is very reactive, and titanium would react readily with it releasing a lot of energy, and the trend goes down with decreasing electronegativities, increasing size of atoms and decreasing electron affinities of the halogens going down the group.

Vibrational frequencies of TiX₄

Vibrational frequencies were also calculated of the TiX₄ species using B3LYP method with LANL2DZ basis set. As the point group of all four compounds is T_d, there are 9 modes of vibration, but only 4 different, as there are degenerate modes. And only two peaks are IR visible, as they change the dipole moment. These are summarised for the T_d point group below, including the calculated vibrational frequencies of the four compounds.

Symmetry label	TiF₄	TiCl₄	TiBr₄	TiI₄	Comment
E	190.9	114.3	71.1	51.3	IR inactive
T₂	217.5	137.3	90.8	67.2	IR active
A₂	717.6	372.2	218.6	149.8	IR inactive
T₂	822.9	501.2	377.9	305.7	IR active; other degenerate vibrations in x and y directions (picture to the right is in z direction)

Above vibrational frequencies follow the trend expected, as increasing mass of halogens decreases the frequency of vibration, by formula $v = 1 / (2 p i) \sqrt{k / μ}$ . Here k is the force constant (relatively corresponding to the bond strength) and $μ$ is the reduced mass.
Comparing the vibrational frequencies of TiF₄ to the ones obtained experimentally^[4], there is a good agreement, as experimentally there is a peak at 800 cm^-1 and at 209 cm^-1 in the gas phase. The solid state will be investigated later.

Molecular Orbitals of TiX₄

Molecular orbitals were also obtained using the B3LYP method with LANL2DZ basis set. The MO orbitals for all the species involve same atomic orbitals, just the energies of the resulting MO orbitals are different. Due to approximations of the LANL2DZ model, the MO's visually are not perfectly matching of the four TiX₄ species, but by close inspection one can tell that the same np and ns atomic orbitals are being used on both X and Ti (d orbitals of Ti are used in bonding as well). As the molecule is highly symmetric, there are a lot of degenarate MO's and so below only one from each set of degenerate orbitals are shown. It is interesting to note that HOMO of the molecule are the lone pairs on X, while the LUMO of the molecule is d_z² along with degenerate d(x²-y².
Below is a table showing molecular orbitals of TiF₄, but one should note that visually the MOs look the same for all four TiX₄ compounds.

No. (down from LUMO)	Comment	Molecular Orbital picture
1	LUMO orbital. This is mainly the d_z2 orbital of Titanium. It is degenerate with d(x²-y²), which is not shown here for space saving purposes
2	HOMO orbital. These are just the lone pair p orbitals of the halogen X. There are three degenerate MOs like this, and only one here is shown.
3	Bonding orbital mostly involving overlapping p orbitals of the halogen X, but a p orbital on Titanium is also involved, although in an anti-bonding fashion. There are 3 degenerate orbitals like this. A better picture is obtained from TiI₄, as the p orbitals are bigger and the overlap is spacially more, thus one can see the overlap between three I atoms, as in contrast with two. The picture given is of TiI₄
4	Bonding orbital involving np orbitals on X and 4s orbital on Ti. The MO picture is given for TiF₄. This is the first orbital which does not match the one in TiI₄, as in the latter this orbital is lower in energy than the ones involing p orbitals on X and d orbitals on Ti, while in TiF₄ it is of higher energy than the Ti(d) + X(p) MO orbitals.
5	Bonding orbital involving Ti(dz²) and X(p) orbitals in bonding fashion. This is the bonding counterpart of the TiX₄ antibonding orbitals. There are two degenerate orbitals of this type: the other one is d(x²-y² with p orbitals on X. This orbital is higher in energy than the next 3 involving the d(xy), d(xz) and d(yz) with p orbitals on X.
6	Bonding orbital involving Ti(d(xz)) and X(p) orbitals. There are three degenerate MOs of this type.
7	Bonding orbital involving p orbitals on Ti and s orbitals on the X ligands. These are very low energy orbitals, and are included only for purposes of interest, as these orbitals do not determine any valuable properties of the molecule as magnetism, color or reactivity. There are 3 degenerate orbitals of this type.

Solid state investigation into TiF₄ and TiCl₄

It has been reported that TiF₄ is a solid while TiCl₄ is a liquid at room temperature and atmospheric pressure. In fluoride, the titanium adopts octahedral structure and forms a trimer Ti₃F₁₅, while TiCl₄ prefers tetrahedral geometry and does not form any type of oligomeric/polymeric structure at room temperature^[5]. This phenomenon has been investigated using B3LYP method with LANL2DZ basis set. First, Ti₃X₁₅^-3 where X=F and Cl were optimized to see if the energetically favourable form is where the fluorine coordinates two titanium atoms, or if the molecules would prefer to not be coordinated together in any way. The results were quite pleasing, as one found that Ti₃F₁₅^-3 does form an oligomeric structure, and fluorine coordinates two Ti atoms, with bond lengths of bridge fluorine Ti-F being 2.01A and of terminal fluorine Ti-F 1.837A. The bond length in tetrahedral fluoride is Ti-F 1.761A, thus one can conclude there is significant bonding in the trimer structure. Opposite if found for the chloride structure, as calculations indicate the atoms are far apart, and the bridging Ti-Cl bond would be 13A, suggesting no bond present. The titanium adopts trigonal bipyramidal structure with bond lengths of Ti-Cl bond being 2.3A, as compared to 2.2A in tetrahedral TiCl₄.

Ti₃F₁₅^-3 unable to publish to d-space	Ti₃Cl₁₅^-3 unable to publish to d-space

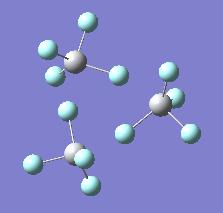
Another calculation was performed on Ti₃F₁₂ trimer and Ti₃Cl₁₂, just to confirm the above investigation with neutral species. The results were once again quite pleasing, just confirming again that titanium fluoride prefers to form oligomeric structures, while the chloride prefers to adopt monomeric structure and not to coordinate. The structures and bond lengths are given below:

Ti₃F₁₂ structure	Ti₃Cl₁₂ structure	Ti-F terminal	Ti-F bridging	F->Ti dative	Ti-Cl terminal	Ti-Cl bridging	Cl->Ti dative
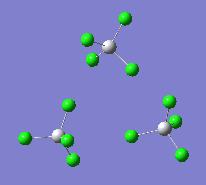		1.7548A	1.8775A	2.1259A	2.1956A	2.1956A	4.69 A

One can see that indeed in the titanium chloride, no dative bonding is present and the compound adopts monomeric tetrahedral structure, thus rendering it liquid, as in contrast to oligomeric structures of titanium chloride, rendering it a solid at room temperature. One might expect some trimer forming in the gas phase of fluoride as well, and that could be checked by weak presence of some additional vibrations in the IR spectrum, but a full IR spectrum of TiF₄ could not be found anywhere in the literature (all 5 references checked that were found using Crossfire, only a few peaks were given without the actual spectra). But presence of trimer structures in the gas phase would be very low, as the temperature is significantly higher than the room temperature, and so the molecule would have enough energy to break apart to constituent monomers.

Vibrational frequencies were calculated for the Ti₃F₁₅^-3 compound. Experimentally, solid-state Raman spectra was recorded before^[4], with the peaks at: 817, 770, 494, 466, 367, 236, 208 and 138 cm^-1. The calculations gave main peaks at: 735, 633, 575, 464, 270 cm^-1. Thus, the calculation of the trimer as having a -3 charge and Ti adopting octahedral structure using B3LYP method with LANL2DZ basis set does NOT give good vibrational frequencies.

Molecular orbitals were investigated of Ti₃F₁₂, just to understand how do the orbitals change upon trimerisation from the tetrahedral one. There are several bonding orbitals which result from this oligomerization, and some of them are presented below:

Molecular orbital diagram	Comment
	A low lying bonding orbital is made by the overlap of three p orbitals on fluorines, which makes the trimer structure favourable
	Another low lying bonding orbital which involves a p interaction between the three fluorines which binds the monomers to a trimer.

Actually, I was not able to find any more bonding orbitals in the pictures obtained from LANL2DZ basis set, as either the pictures were unclear, or there were only anti-bonding interactions. One would expect, however, that the p orbitals on bridging fluorines overlap with p or d orbitals of titanium.

Log files for gaussian

As d-space does not accept my Gaussian log files, I have uploaded them here:
Ti3Cl12 opt freq mo: https://www.ch.imperial.ac.uk/wiki/images/4/45/Ti3cl12_lanl2dz_opt_freq_mo.out
Ti3F12 opt freq mo: https://www.ch.imperial.ac.uk/wiki/images/7/71/Ti3f12_lanl2dz_opt_freq_mo.out
Ti3Cl15(3-) opt freq mo: https://www.ch.imperial.ac.uk/wiki/images/b/b1/Ti3cl15_lanl2dz_opt_freq_mo.out
Ti3F15(3-) opt freq mo: https://www.ch.imperial.ac.uk/wiki/images/a/ad/Ti3_f15_lanl2dz_opt_freq_mo.out
and as one of the TiX4 examples, TiF4: https://www.ch.imperial.ac.uk/wiki/images/3/38/TIF4_OPT_FREQ_MO.LOG

References

↑ E.C. Alyea, G. Ferguson, S. Kannan, Acta Cryst. (1996), C52, 765-676 DOI:10.1107/S010827019600100X
↑ G.J. Kubas, J. Chem. Soc., Chem. Commun., 1980, 61-62, DOI:10.1039/c39800000061
↑ C.G. Kreiter, Inorganica Chimica Acta, Vol 284, 2, 1999, 229-236 DOI:10.1016/S0020-1693(98)00293-X
↑ ^4.0 ^4.1 I.R. Beattie, P.J. Jones, J. Chem. Phys. 90, 5209 (1989) DOI:10.1063/1.456542
↑ C. Housecroft, Inorganic Chemistry, 2nd edition, 2004

[S010827019600100X-1] E.C. Alyea, G. Ferguson, S. Kannan, Acta Cryst. (1996), C52, 765-676 DOI:10.1107/S010827019600100X

[c39800000061-2] G.J. Kubas, J. Chem. Soc., Chem. Commun., 1980, 61-62, DOI:10.1039/c39800000061

[S0020-1693(98)00293-X-3] C.G. Kreiter, Inorganica Chimica Acta, Vol 284, 2, 1999, 229-236 DOI:10.1016/S0020-1693(98)00293-X

[1.456542-4] 4.0 ^4.1 I.R. Beattie, P.J. Jones, J. Chem. Phys. 90, 5209 (1989) DOI:10.1063/1.456542

[Housecroft-5] C. Housecroft, Inorganic Chemistry, 2nd edition, 2004

[1]

[2]

[3]

[4]

[5]

BCl3 introduction module

COCl2 optimization

BH3 vibrations

Molecular Orbitals of BH3

Isomers of Mo(CO)4(P(CH3)3)2