Rep:Mod:mj506 mod1

The Hydrogenation of cyclopentadiene dimer

In this exercise, molecules have been drawn using ChemBio3D and geometry optimizations have been done using MM2 Molecular Mechanics method. Strain energies have been calculated. Minimum RMS gradient was set to 0.010. Temperature was set to 300 K.

Exo dimer product. Total energy: 31.8766 kcal/mol.

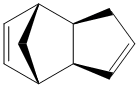
Endo dimer product. Total energy: 33.9975 kcal/mol.

From the total energies above, the exo product is thermodynamically more stable. But in practice, the endo dimer is produced. It can be concluded that the reaction is kinetically controlled, as thermodynamically less stable compound is made. Hence MM2 method is not sufficient for such reactions, as it cannot account for why the kinetic product is formed. More sophisticated methods (involving electronic properties) must be used in order to account for such reactivities.

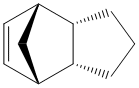
Dihydro derivative 1 of the endo dimer.

Total energy: 35.9267 kcal/mol. Breakdown of the contributory terms:

Stretch: 1.2353
Bend: 18.9364
Stretch-Bend: -0.7610
Torsion: 12.1278
Non-1,4 VDW: -1.5037
1,4 VDW: 5.7288
Dipole/Dipole: 0.1631

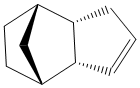
Dihydro derivative 2 of the endo dimer.

Total energy: 31.1521 kcal/mol. Breakdown of the contributory terms:

Stretch: 1.0965
Bend: 14.5236
Stretch-Bend: -0.5494
Torsion: 12.4981
Non-1,4 VDW: -1.0697
1,4 VDW: 4.5124
Dipole/Dipole: 0.1406

Comparison of 1 and 2

Thermodynamically, the dihydrogenated derivative 2 of the endo dimer is more stable than the derivative 1. Comparing the contributory terms of the total strain in the molecule, the most profound change is in the bending energy, which goes to 14.5 from 18.9, a change of 4.4 kcal/mol. Changes in stretching, torsion, Van der Waals forces are not that significant and can be disregarded. There are no hydrogen bonding in the molecules.

Examining results from the MM2 calculation in more detail, it can be seen that the biggest contribution to bending strain comes from the double bond in derivative 1. Angles of the C=C-C bonds are supposed to be around 120^o, but they are calculated to be 107.6 due to fused rings strain. This is not the case for derivative 2, as the cyclopentadiene ring in which the double bond is located is not that strained as in the former derivative. A significant contribution to the strain of the molecule comes from torsional strain. As the molecule is very rigid (consequence of two rings fused), most of the carbon conformations (specifically, hydrogens) are eclipsed, and thus increase the energy of the molecule. Most of the dihedral angles between hydrogens are 10-30^o, indicating torsional strain. This can be seen in the model below:

Pentahelicene

Literature reports of hydrogenation of dicyclopentadiene shows that under conditions of H₂ and Pd/Al₂O₃ first gives the thermodynamic product and upon further hydrogenation will give the tetrahydro compound. Thus, the dihydrogenation reaction favours 2 derivative and is thermodynamically controlled.

Stereochemistry of Nucleophilic additions to a pyridinium ring (NAD⁺ analogue)

ChemBio3D software was used to build a model of the proline derivative 3. MM2 method was used to optimize the geometry, and a final energy of 25kcal/mol was obtained. Its structure is given on the right. A key feature of the structure is the fact that the C=O group is pointing above the pyridine ring by 43.1^o, and thus when MeMgI is attacking, Mg first associates with oxygen, and then Me^- attacks the pyridinium ring from the same face as the C=O group. It was not possible to optimize the molecule with MeMgI associated to it, as MM2 does not identify Mg atom. Mechanism is shown below:

Molecule 4 was optimized to two possible conformers 4A (15kcal/mol) and 4B (17kcal/mol). Position of the carbonyl group in the 4A derivative is the same as in the 3 derivative, the C=O group is pointing upwards from the plane of pyridinium ring by 42.4^o, to the same plane as the upwardly pointing methyl group in the 7-membered ring. But for 4B derivative the carbonyl group is pointing to the opposite direction, down by 40^o. Addition of aniline occurs to the opposite face of the pyridinium ring compared to carbonyl group, as it has been shown experimentally [2]. This happens due to steric hindrance exhibited by oxygen on the aniline, and so aniline is rendered to come from the direction opposite oxygen. One might expect a similar behaviour as for the 3 compound, i.e., hydrogen bonding by amine to oxygen and then nucleophilic attack by nitrogen on the pyridine ring, but experimentally that is not the case. It might also be that the reference above did not obtain 4A conformation, as although the energy difference between 4A and 4B is only 2 kcal/mol, that requires a conformational changed in a cycloheptane ring which is fused to two benzene rings, hence very energetically unlikely.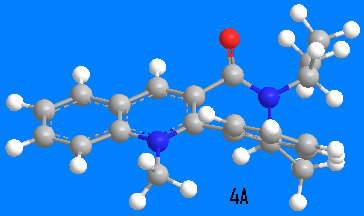

and
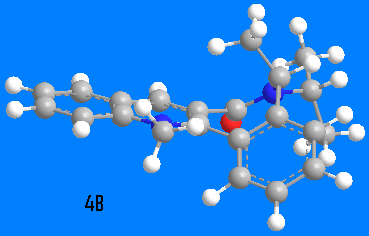
MM2 optimization was attempted on the aniline derivative of 4A and 4B, but with erroneous results, as benzene rings were rearranged to chair conformation, which shows the inherent drawbacks of MM2 approach.

Stereochemistry and Reactivity of an intermediate in the Synthesis of Taxol

Two isomers of the intermediate in the synthesis of Taxol have been built in ChemBio3D and optimized using MM2 method. Compound 5A has 120kcal/mol energy, having its C=O group pointing to the same face as cyclopentane ring. The major strain in this molecule comes from bending of the carbonyl group, resulting in C-(C=O)-C bond angle of almost 180^o. Compound 5B has strain energy of 44kcal/mol and has the C=O group pointing to the same direction as the cyclopentane ring. Thus, the more stable atropisomer 5B would be expected to be found after letting the isomers to equilibrate. The cyclohexane ring was initially optimized to a boat conformation, but by manually editing the structure, it was re-set to chair conformation. That reduced the energy by 2kcal/mol.
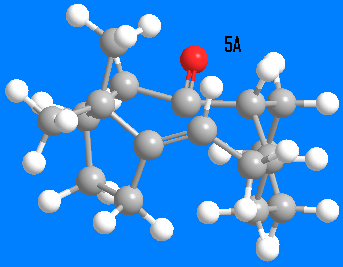and

In both isomers, the alkene bond releases some bending strain, as the cyclononane ring is strained by the two rings (cyclohexane and cyclopentane). By going from sp2 to sp3 hybridization upon alkene functionalization, strain energy due to bending would be increased. By hydrogenating 5B isomer and MM2 optimizing it yielded energy of 53 kcal/mol, which is 10 kcal/mol higher than for unhydrogenated alkene. Although comparison of MM2 optimization energies of different molecules is somewhat unreliable, the structure did not undergo major rearrangements, but only two more hydrogens were added, so molecules can be vaguely compared. This significant difference arises when functionalizing the alkene with hydrogens, thus the difference would be much higher for more bulkier substituents. The inherent gain of steric strain upon functionalization is the main reason why alkene is reluctant to react and these reactions are very slow.

How one might induce room temperature hydrolysis of a peptide

Cis-decalin model peptide breaking

Compound 6A was built with ChemBio3D. OH group is axial and amide group equatorial. Energy was minimized to 15.6 kcal/mol. Creating the ester linkage and breaking NH2 bond, and then optimizing it using MM2 method gave energy of 35 kcal/mol. Arranging C=O group to be close to O-H, at 180pm, hydrogen bonding is viable. But that leaves 300pm distance between C=O carbon and the O-H oxygen. As the atoms are fixed due to being attached to rings, it is difficult for the molecule to rearrange in a way so carbon could be attacked by oxygen lone pair at 109^o (the Burgi-Dunitz angle). Thus this reaction would be slowed down. Compound 6B had both OH and amide groups equatorial and had energy of 13.1 kcal/mol. Distance between O-H---O=C is 180pm, which is sufficient for hydrogen bonding. Thus, the molecule orientates itself so that energy is lowered due to hydrogen bonding. Modifying this compound to have the ester bond instead of amide, and running MM2 optimization again, yields energy of 25.5 kcal/mol. It is clear from the data above, comparing strain energies, that the compound prefers OH-equatorial, amide-equatorial positions in both pre-ester and ester forms. Also, as the amide group and OH are both equatorial and thus parallel to each other, C=O can rotate along a single-bond easily to orientate itself at the Burgi-Dunitz angle with respect to oxygen lone pair. This reaction would be fast. Another two possibilities of the above compounds could be when the amide group is axial. But then distances are even greater for reaction to occur between C=O and O-H and so can be disregarded.

Trans-decalin model peptide breaking

Compound 7A has OH group axial and amide group equatorial. Hydrogen bonding between C=O and O-H is viable, as the distance is 180pm. Optimized energy (MM2 method) was 9 kcal/mol. Again, oxygen is 300pm away from the carbonyl carbon, and as atoms are conformationally fixed due to decalin rigidity, reaction would be very slow. Ester has a total energy of 29.1 kcal/mol. Compound 7B has both OH and amide groups axial. Hydrogen bonding between C=O and O-H is viable, as the distance is 180pm. Optimized energy was 12 kcal/mol. Ester of 7B has a total energy of 26.3 kcal/mol, thus stabler than ester of 7A. As per above, amide and carbonyl are parallel to each other, and to achieve Burgi-Dunitz angle, only rotation around single bond is required, thus the reaction would be fast. But because 7A is stabler by 3kcal/mol, peptide bond breaking would be in two steps: first transition from 7A to 7B, and then esterification. 7A would be the majority conformation, and thus the rate determining step of the esterification would be the transition from 7A to 7B, so the reaction would be slower than for 6 stereoisomer. Contrary to compound 6, OH-equatorial derivative of this compound is impossible, as the trans-decalin would be fused with axially connected carbons, which would add massive strain on the molecule. These amides are hence not investigated.

Regioselective addition of dichloromethane

Compound 8 (right) was drawn using ChemBio3D and optimized using MM2 method. Total energy obtained was 17.9 kcal/mol. Both double bonds were calculated to be 1.339 A. C-Cl bond distance was 1.76 A. Then 8 was optimized using HF/STO-3G method using Gaussian software. C=C double bonds changed to 1.308 A and C-Cl changed to 1.797 A. C-C and C-H single bonds slightly decreased as well. That should reflect the actual geometry of the molecule better, as in contrast to MM2, the HF method is quantum mechanical (semi-empirical), and accounts for electronic interactions, while MM2 is purely classical mechanical method, and thus does not take into account any electronic effects.
Molecular orbitals were obtained and are illustrated below:

Geometry optimization and vibrational frequencies have also been calculated using DFT method B3LYP/6-31G(d). C=C double bond anti to C-Cl bond was 1.335A long, and the syn one was 1.332 A, suggesting the C=C double bond syn to C-Cl bond is stronger. Bond distances obtained from DFT calculations agree almost perfectly with ones obtained from X-ray diffraction experimentally. The syn bond being stronger is further proved by the fact that vibrational frequency for C=C stretch of the syn bond is 1760 cm^-1 while for the anti one is at 1740 cm^-1, suggesting a stronger force constant for syn and hence stronger bond.
Another interesting observation is the fact that carbon to which chlorine is attached, is closer to carbons in the anti double bond by 0.255 A than to the syn double bond carbons (from DFT calculation). In the article, that is attributed to a reason which can be seen by looking at the HOMO-1 and LUMO+2 diagrams above, where one can see that the antibonding orbital LUMO+2 can mix with the bonding HOMO-1 orbital, however, in the article authors claim it is a bonding interaction and thus energy of bonds is lowered, although one can see from the diagrams that the actual interaction would be antibonding.

Upon monohydrogenation of the anti double bond, vibration at 1740 cm^-1 disappears as expected, but the syn bond vibration decreases from 1760 -> 1757 cm^-1 suggesting the bond strength slightly decreases. That is confirmed by the bond distance changing from 1.332A -> 1.333A. That can be explained by the fact that distance between the double bond and chlorine increases slightly 3.44871A -> 3.45548A and as seen from HOMO diagram, orbital on chlorine is participating in the bonding as well, and change in geometry will result in change in bond strength on C=C double bond.

As for the C-Cl stretching frequencies, in order of decreasing intensity, there are several at: 773 cm-1, 932 cm-1, 1046 cm-1, 549 cm-1, 903 cm-1. When the compound is monohydrogenated, almost all of above vibrations increase in frequency, suggesting a stronger C-Cl bond, which would again suggest a disappearance of LUMO+2 (essentially C-Cl antibonding orbital) interaction with HOMO-1 (anti double bond bonding orbital). The new vibrational frequencies are: 782 cm^-1, 944 cm^-1, 1046 and 549 dissapeared completely, and 912 cm^-1. It must also be noted that these vibrations involve not only the C-Cl bond stretching, but also bending and stretching of C-H and C-C simulateniously in the rings. So these changes could be due to double bond changed to single carbon-hydrogen bonds, and them being subject to different strain than C=C double bond, and so different stretching frequencies.

Both, the hydrogenated and non-hydrogenated derivatives of compound 8 have C_S symmetry, as they have a plane of reflection going along double bond and C-Cl bond.

It is interesting to note that bond lengths as calculated with MM2 are closer to the DFT obtained ones, and so it suggests that initially MM2 gave better geometry of the molecule than HF method, although latter being more quantum mechanical.

Total energies of molecules are given below:
From HF:
Total energy of diene: -873.6 Hartrees
Total energy of monohydrogenated diene: -884.5 Hartrees
From DFT:
Total energy of diene: -887.13 Hartrees
Total energy of monohydrogenated diene: -888.36 Hartrees
It can be concluded that hydrogenation did not significantly decrease the energy of the molecule, as one would expect upon hydrogenating a double C=C bond. That suggests double bond anti was stabilized by LUMO+2 quite significantly.

Hydroboration/oxidation of (4R)-(+)-p-menthene

Hydroboration / oxidation of compound 1 yields two diastereoisomers (2R,5R)-(+)-carvomenthone 2 and (2S,5R)-(+)-carvomenthone 3, which can be easily separated by fractional distillation or column chromatography and characterized by ¹H NMR, ¹³C NMR, and optical rotation measurement. The identification of the corresponding diastereoisomer using the above mentioned techniques is the goal of this paper. Experimentally the work has been carried out by D. Schneider and S. Viljoen. Experimental ¹H NMR, ¹³C NMR and optical rotation have been used from that article.

The following reaction takes place:

Compounds are diastereoisomers and spectroscopically they can be distinguished with ¹H NMR, X-ray diffraction and optical rotation measurements. Dihedral angles between adjacent hydrogens will differ for these compounds and it is easiest to see the differences using ¹H NMR. For example, in compound 2 the methyl group is equatorial and will render the other hydrogen on the carbon axial, and it will have -59^o and -176^o degree dihedral angles with hydrogens on the adjacent carbon. This will thus be reflected in ¹H NMR scalar coupling constants, as given by Karplus equation. The ¹H NMR spectra coupling constants can be predicted using Janocchio. ¹³C NMR spectra (decoupled) can be predicted using advanced DFT calculations. Optical rotation can be computationally predicted as well. X-ray diffraction is not possible yet.

NMR spectra

First, spectra will be calculated for compound 2. Isopropyl is quite bulky, and in order to minimize energy, the isopropyl group will be fixed at the equatorial position, and that will render methyl group equatorial as well. Structure was modified to be in the chair conformation, and all conformations were set to staggered. MM2 was run on the molecule, and total energy of 13.0 kcal/mol was obtained. Structure was saved as a Gaussian job, and optimized using mpw1pw91/6-31(d,p) method and basis set. The new coordinate file was saved and NMR spectra of the compound was obtained using mpw1pw91/6-31(d,p) NMR scrf(cpcm,solvent=chloroform). Molecular model of the final conformation of the molecule is given below:

Pentahelicene

Conformation was changed at carbon 5 so carbons 2 and 3 are in the same environment (as much as possible), as seen from the above Jmol model, the conformation is so those carbons are in slightly different environments. Consequently, the ¹³C NMR shifts agree better with the experimental values.

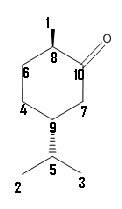
¹³C NMR spectra values obtained experimentally and computationally are given in the table below:

¹³C NMR chemical shifts from experimental and computational data

Carbon number	Shift/ppm experimental	Shift/ppm calculation #1	Shift/ppm calculation #2	Shift/ppm of 3 calculated
1	14.8	16.0	16.4	18.3
2	19.3	16.6	21.4	21.2
3	19.6	22.1	21.9	21.8
4	28.9	31.6	30.4	25.3
5	32.8	33.7	34.8	32.2
6	35.1	35.2	35.5	35.4
7	44.9	41.2	44.8	43.2
8	45.4	45.2	46.5	44.9
9	46.6	45.7	46.7	46.0
10	213.6	210.1	209.5	212.5

¹³C NMR spectra of compound 3 could not be obtained from the literature, as apparently it has never been recorded, at least according to XFire. ¹³C NMR spectra was still calculated using mpw1pw91/6-31(d,p) method for comparison. Conformation chosen was the same as for #2 NMR calculation for compound 2, except the methyl group was rendered axial (as it is the diastereisomer).

Optical Rotation

Value for optical rotation reported in the literature is [α]_D²⁰=+11.1(neat). Optical rotation has been calculated using b3lyp/aug-cc-pvdz method/basis set. The value obtained is +21.93^o, almost twice as much as the experimentally observed. The difference is attributed to a possibly different conformation/conformations which are present in the sample. This fact is also proved by the ¹³C NMR above, as one can see that the chemical shifts do not exactly match the calculated values, pointing to a different/other conformations present, and thus an average is obtained experimentally, while that is not possible computationally.
Another conformation was chosen for optical rotation calculation, by setting both substituents axial (the energetically unfavourable state). Optical rotation value obtained was +110.38, which is even worse than above. If this was a negative value, one could try and calculate how much of this conformer is at room temperature, and then average the optical rotation, but as it is significantly bigger, there is another conformation which is present, with a much lower optical rotation and higher population.