Rep:Mod:milandeleevTS

Introduction

What is a Transition State?

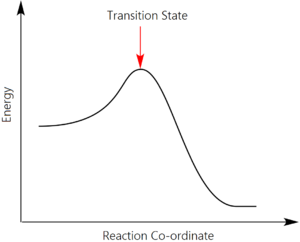
According to the IUPAC Gold Book, the transition state of an elementary reaction 'is that set of states (each characterized by its own geometry and energy) in which an assembly of atoms, when randomly placed there, would have an equal probability of forming the reactants or of forming the products of that elementary reaction' ^[1]. Represented diagrammatically in the form of an energy profile, the transition state references the maximum of the graph, at which point the activated complex can 'fall' back to the reactants or forward to the products with equal probability.

What is a Potential Energy Surface (PES)?

A potential energy surface is essentially a three-dimensional extension of the energy profile. Likewise, the transition states thereon are represented by local maxima. The minima of such surfaces are the lowest-energy areas in the locality, and are thus representative of the reactive intermediates (which are defined as the products of single elementary reactions), as well as the reactants and products. Consequently, both the transition states and intermediates can be found by differentiation to elucidate the gradient: at both points, the gradient should be zero. If the second derivative (curvature) is found to be negative, the point is a local maximum and is a transition state. If the curvature is positive, the point is a local minimum and is an intermediate, reactant or product.

Nf710 (talk) 09:19, 17 November 2017 (UTC) This is a good answer, if you are talking in 1 dimension. However the PES in Guassian has 3N-6 dimensions. The second derivative sat the minimum are positive for all dimensions. The second derivative at the TS are positive for all dimensions except 1 which is negative and that is the reaction coord, hence why it is called a saddle point.

Exercise One

(Fv611 (talk) Very good: concise and correct answers to the whole exercise. You could have pushed the discussion a bit further, especially with respect to the energy levels of your MOs.)

Which Reaction is being Considered?

The Diels-Alder addition of 1,3-butadiene to ethene can be categorised using the Woodward-Hoffmann rules. 1,3-butadiene is a a $_{4} π_{s}$ component, and ethene is a $_{2} π_{s}$ component. Consequently, $(4 q + 2)_{s} + (4 r)_{a} = 1$ , so the reaction is thermally allowed. To model this reaction and its transition state, the reactants and product were first constructed in Gaussian and optimised at a PM6 level. Subsequently, the cyclohexene molecule was copied, the bond lengths and angles altered to better resemble the transition state, and then optimised to a Berny transition state using the same parameters.

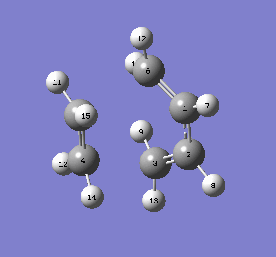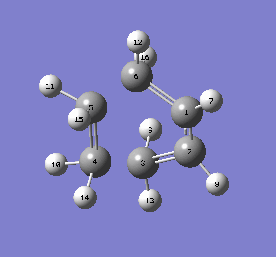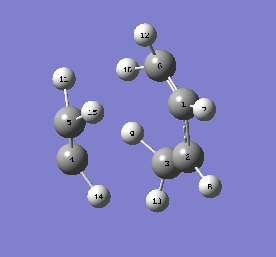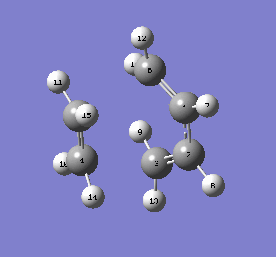
TS Vibrations and Bond Formation Synchrony

To confirm that the transition state was correct, IRC and frequency calculations were ran thereon. The imaginary frequency of the transition state did indeed resemble the reaction, and was found at -949.59cm^-1. The IRC was also successful. The GIFs are below. Both prove that the formation of both bonds is synchronous.

Vibrations

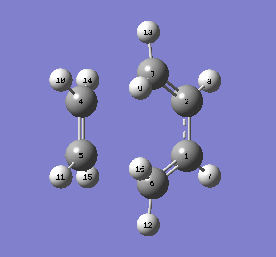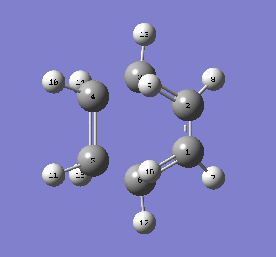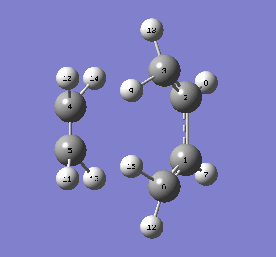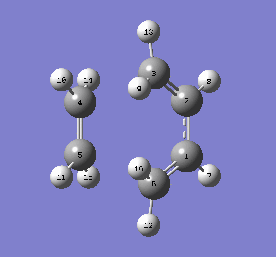IRC (reaction pathway)

Bond Lengths

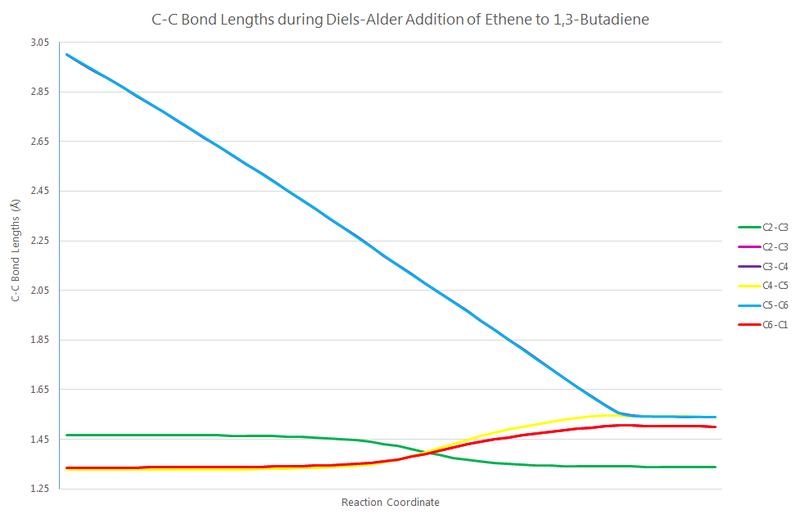
**Transition State Bond Lengths**
Carbons	Bond Length (pm)
C1-C2	141
C2-C3	138
C3-C4	211
C4-C5	138
C5-C6	211
C6-C1	138

The C(sp²)-C(sp²) single-bond length in the butadiene reactant is ca. 147pm (C1-C2); the C(sp³)-C(sp²) single-bond length in the cyclohexene product is ca. 150pm (C2-C3; C6-C1); and the C(sp³) C(sp³) single-bond length in the cyclohexene product is ca. 154pm (C3-C4; C4-C5; C5-6). The transition state bond lengths are tabulated adjacent. Since the general consensus on the van der Waals radius of the carbon atom floats around 170pm, the transition state shows that there is some level of bonding between all of the carbon atoms (as the interatomic distances all deceed twice the vdW radius of 340pm). The bond lengths throughout the whole reaction are graphed below.

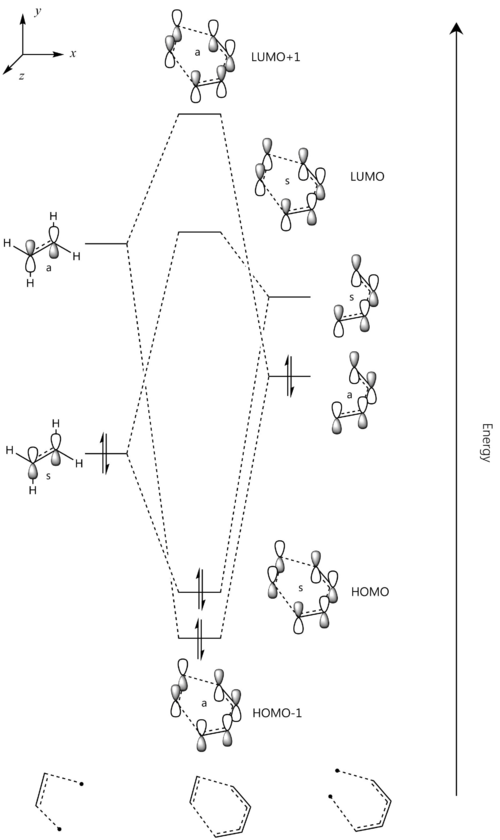
Molecular Orbital Analysis

The transition state and reactant models were used to visualise the molecular orbitals involved in the reaction, as can be seen below. Please use the MO diagram on the right of the table as a reference. From the below table, it can clearly be seen that only molecular orbitals of the same symmetry may interact to form further MOs. This is because, mathematically, the integral of an anti-symmetric function is zero. The product of a symmetric and anti-symmetric function is an anti-symmetric function, whilst the product of two symmetric or two anti-symmetric functions is a symmetric function. Thus only when two MOs of the same symmetry (both either symmetric or anti-symmetric) are overlapping can the overlap integral be nonzero.

Ethene MO	1,3-Butadiene MO	Symmetry	Resultant Transition State MOs
LUMO	HOMO	$a$	HOMO-1
LUMO	HOMO	$a$	LUMO+1
HOMO	LUMO	$s$	HOMO
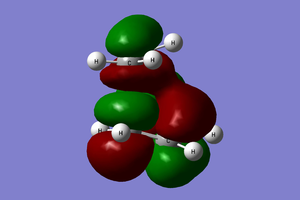HOMO	LUMO	$s$	LUMO

.LOG Uploads

cis-Buta-1,3-diene

trans-Buta-1,3-diene

Ethene

Transition State

Intrinsic Reaction Coordinate

Cyclohexene

Exercise Two

Which Reaction is being Considered?

This question regards the reaction of cyclohexa-1,3-diene with 1,3-dioxole. This Diels-Alder cycloaddition has two possible products: the exo and endo adducts. The former is the thermodynamic product; it is stabler than the endo adduct because it minimses intramolecular repulsions. However, kinetically, the endo is favoured due to more efficient orbital overlap. Hence, in irreversible reactions, the endo product is favoured due to a lower activation barrier (the endo rule). The GIFs below demonstrate the two pathways of reaction:

endo Diels-Alder	exo Diels-Alder

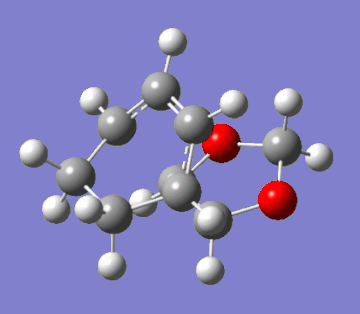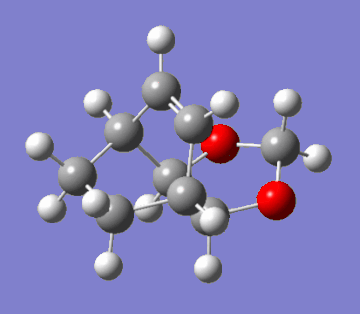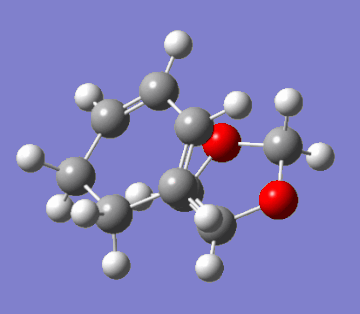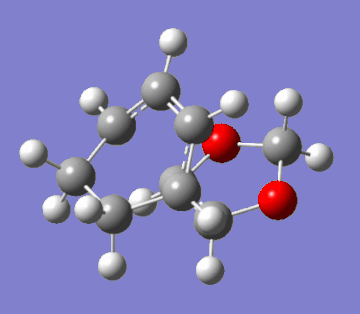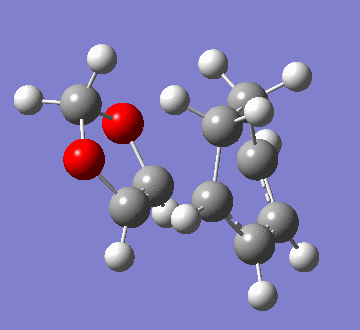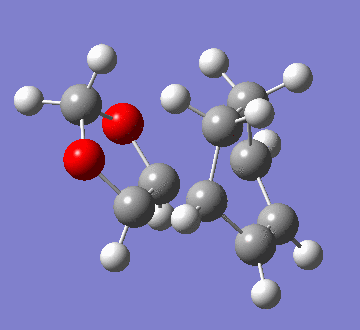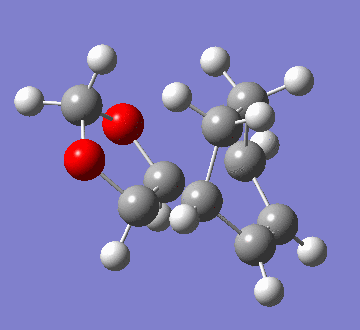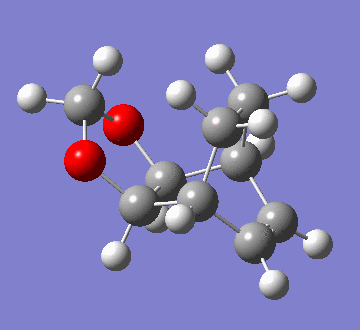
Generating Molecular Energies

**Calculated Reactant and Product Energies to 2 d.p (kJmol^-1)**
	Compound	$ε_{0} + E_{t} o t$	$ε_{0} + H_{c o r r}$	$ε_{0} + G_{c o r r}$
Reactant	Cyclohexa-1,3-diene	-612505.40	-612502.93	-612593.19
Reactant	1,3-Dioxole	-701108.59	-701106.12	-701187.43
Product	exo Diels-Alder Adduct	-1313747.19	-1313744.71	-1313854.07
Product	endo Diels-Alder Adduct	-1313741.42	-1313738.94	-1313849.34

The reactants, products and transition states were optimised at the 6-31G(d) level. Analysis of the .LOG file allows the elucidation of the component energies, which are tabulated adjacent. The results can be used to calculate the standard Gibbs free energy changes (Δ_rG^Ø) and equilibrium constants (K_eq). The activation energies (Δ_rG^‡) are obtained from the 'Sum of electronic and thermal Free Energies' line in the .LOG files of the transition states, from which the reactant energy is subtracted.

Δ_{r} G^{⊖} (298.15 K) = \sum_{p r o d u c t s} (ε_{0} + G_{c o r r}) - \sum_{r e a c t a n t s} (ε_{0} + G_{c o r r})

K_{e q} = \exp - (\frac{Δ_{r} G^{⊖} (298.15 K)}{R T})

Applying the Equations

Thus, for the currently-considered reactions, in kJmol^-1:

\sum_{r e a c t a n t s} (ε_{0} + G_{c o r r}) = - 612593.20 + (- 701187.43) = - 1313780.63

Using this result, the below data are generated. All data are in kJmol^-1, aside from K_eq, which has units of mol^-1dm³.

**Gibbs Free Energies of Reaction and Activation**
$\sum_{r e a c t a n t s} (ε_{0} + G_{c o r r})$	Product	$ε_{0} + G_{c o r r}$	$Δ_{r} G^{⊖} (298.15 K)$	$K_{e q}$	$Δ_{r} G^{‡}$
-1313780.63	exo Diels-Alder Adduct	-1313854.07	-73.44	7.359 × 10¹²	166.29
-1313780.63	endo Diels-Alder Adduct	-1313849.34	-68.71	1.092 × 10¹²	158.47

Analysing the Results

These calculations confirm the previous assertions that the exo product is stabler but less kinetically accessible. The endo adduct is less thermodynamically stable (by 4.73kJmol^-1), as the reaction to form it has a less negative Gibbs free energy. However, it is kinetically preferred, as the activation barrier to formation is 7.82kJmol^-1 lower than for the exo adduct.

Nf710 (talk) 09:29, 17 November 2017 (UTC) This is not correct unfortunatly, I assume that you have calculated the energies incorrectly. make sure you use Sum of electronic and thermal Free Energies in the thermochemistry.

Molecular Orbital Analysis

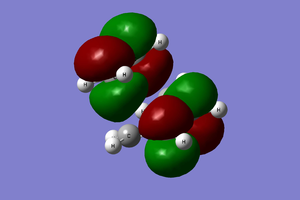
The first reaction considered (ethylene with 1,3-butadiene) was a normal Diels-Alder reaction, because the diene was electron-rich and the dienophile electron-deficient, meaning that the diene HOMO was higher than the dienophile HOMO. This reaction, however, is a reaction with inverse electron demand, which means that the dienophile HOMO is more energetic than the diene HOMO. This is because the dienophile, in this case, is quite electron-rich, due to the inductively electron-releasing oxygen atoms present alpha to the double bond. This theory can be confirmed by an energetic analysis of the MOs in the transition state.

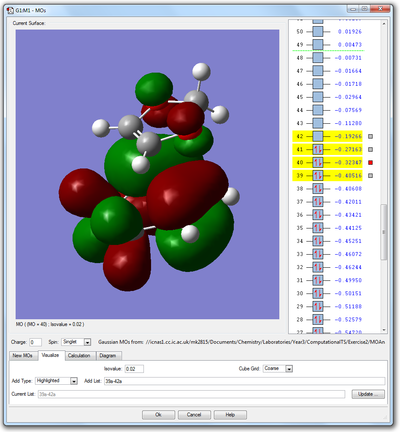It is clear in the images above that the 40th MO of the transition state is mainly comprised of the HOMO of the cyclohexadiene, whilst the 41st MO almost completely resembles the HOMO of the dienophilic dioxole. Since the HOMO of the dienophiile is higher than the diene HOMO by ca. 136.1kJmol^-1, this is an inverse electron demand. This is reflected in the MO diagram below.

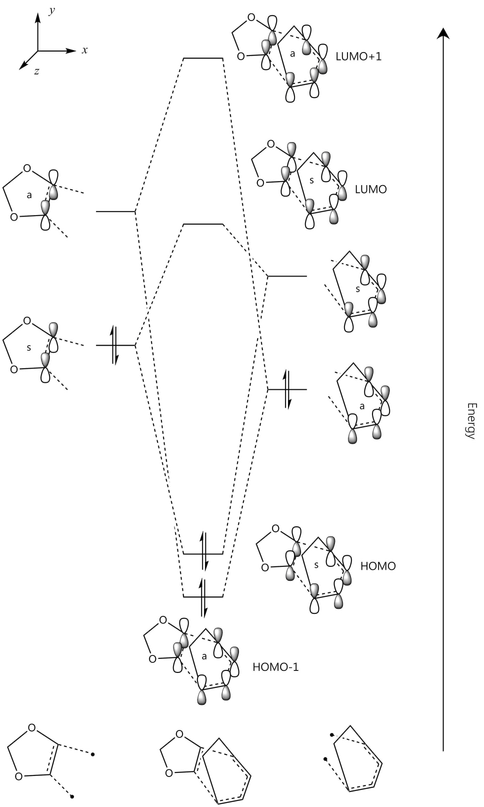
Molecular Orbital Functions

Cyclohexa-1,3-diene MO	1,3-Dioxole MO	Symmetry	Resultant endo Transition State MOs	Resultant exo Transition State MOs
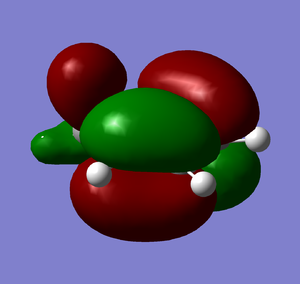HOMO	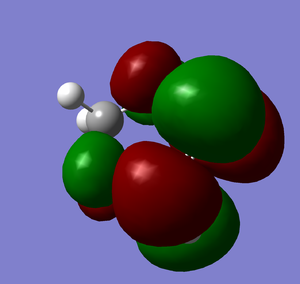LUMO	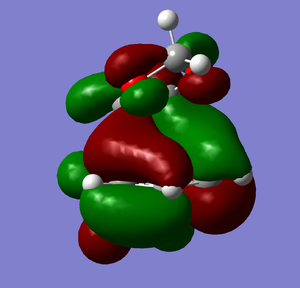$a$	HOMO-1	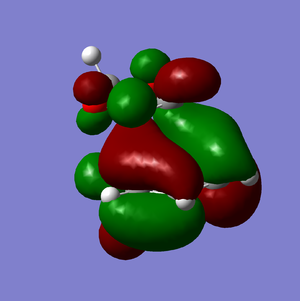HOMO-1
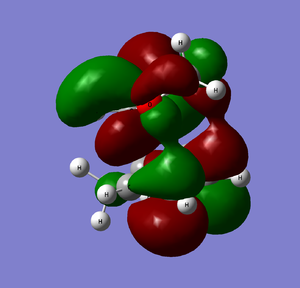HOMO	LUMO	$a$	LUMO+1	LUMO+1
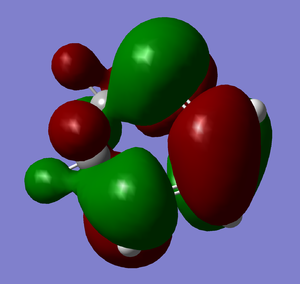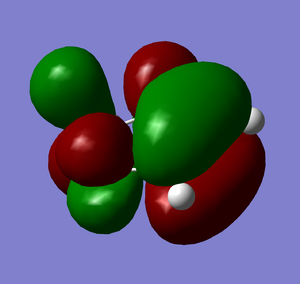
LUMO	HOMO	$s$	HOMO	HOMO
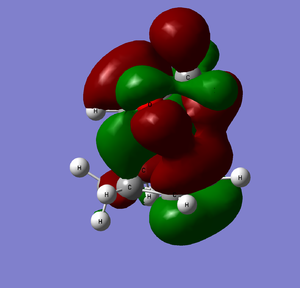
LUMO	HOMO	$s$	LUMO	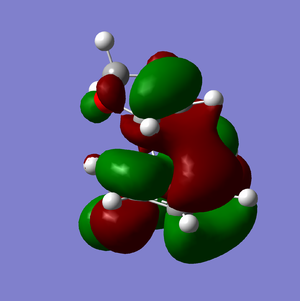LUMO

It is clear from comparing the transition state HOMOs for the exo and endo adducts why the endo adduct is kinetically favoured: there are secondary non-bonding interactions present between the reactive site of the diene and the p-orbitals of the oxygen atoms on the dienophile. These interactions stabilise the transition state, reducing its energy and therefore decreasing the activation energy Δ_rG^‡. Due to the geometry, these interactions are impossible on the exo transition state.

.LOG Uploads

1,3-Dioxole

1,3-Cyclohexadiene

endo Diels-Alder Adduct

Transition State for endo Diels Alder Adduct

Intrinsic Reaction Coordinate for endoDiels-Alder Adduct

exo Diels-Alder Adduct

Transition State for exo Diels Alder Adduct

Intrinsic Reaction Coordinate for exoDiels-Alder Adduct

Calculation for Ordered MOs in Transition State

Nf710 (talk) 09:30, 17 November 2017 (UTC) This is a good section you have shown the SOO nicely for the endo TS. It would have been nice if you could have shown more understanding about the quantum methods.

Exercise Three

Which Reaction is being Considered?

This question deals with the reaction of sulphur dioxide with o-xylylene. This reaction has three possible products: the exo Diels-Alder adduct, which is the thermodynamic (more stable) D-A product, the endo Diels-Alder adduct, which is the kinetic (more favoured by orbital overlap) D-A product, and the cheletropic adduct. The GIFs below demonstrate these reaction pathways. These GIFs also illustrate the significant instability of the o-Xylylene reactant. One of the unsaturated exocyclic bonds is simply bursting to become endocyclic, driven by the attainment of aromaticity, which can be seen in the GIFs by how quickly the electron density moves from the exocyclic alkene bond into the ring to form a phenyl component. This theory can be confirmed by the fact that o-Xylylene quickly isomerises in normal conditions via an electrocyclic reaction into benzocyclobutene.

endo Diels-Alder	exo Diels-Alder	Cheletropic

Generating Molecular Energies

**Calculated Reactant and Product Energies to 4 s.f (kJmol^-1)**
	Compound	$ε_{0} + E_{t} o t$	$ε_{0} + H_{c o r r}$	$ε_{0} + G_{c o r r}$
Reactant	o-Xylylene	573.7	576.2	468.7
Reactant	Sulphur Dioxide	-239.0	-236.5	-311.4
Product	Cheletropic Adduct	114.4	116.9	0.01050
	exo Diels-Alder Adduct	173.4	175.8	56.3
	endo Diels-Alder Adduct	175.2	178.4	57.0

The drawing and subsequent optimisation of all of the components of the reaction at a PM6 level allows the elucidation of the component energies through analysis of the .LOG file. These energies are tabulated adjacent. As above, the results are used to calculate the standard Gibbs free energy changes (Δ_rG^Ø), equilibrium constants (K_eq) and activation energies (Δ_rG^‡).

Applying the Equations

Thus, for the currently-considered reactions, in kJmol^-1:

\sum_{r e a c t a n t s} (ε_{0} + G_{c o r r}) = 468.7 + (- 311.4) = 157.3

Using this result, the below data are generated. All data are in kJmol^-1, aside from K_eq, which has units of mol^-1dm³.

**Gibbs Free Energies of Reaction and Activation**
$\sum_{r e a c t a n t s} (ε_{0} + G_{c o r r})$	Product	$ε_{0} + G_{c o r r}$	$Δ_{r} G^{⊖} (298.15 K)$	$K_{e q}$	$Δ_{r} G^{‡}$
157.3	Cheletropic Adduct	0.01050	-157.3	3.624 × 10²⁷	102.8
	exo Diels-Alder Adduct	56.3	-101.0	4.959 × 10¹⁷	84.4
	endo Diels-Alder Adduct	57.0	-100.3	3.739 × 10¹⁷	80.5

Analysing the Results

It is clear that the cheletropic adduct is thermodynamically far more stable than either of the Diels-Alder adducts, by more than 50kJmol^-1. However, the Diels-Alder reaction has a lower barrier of activation by at least 18kJmol^-1, which confirms that the Diels-Alder reaction is more kinetically accessible. Overall, the kinetic product of the reaction between o-Xylylene and sulphur dioxide is the endo Diels-Alder adduct, and the thermodynamic product is the cheletropic adduct. This is illustrated graphically in the form of a reaction profile below.

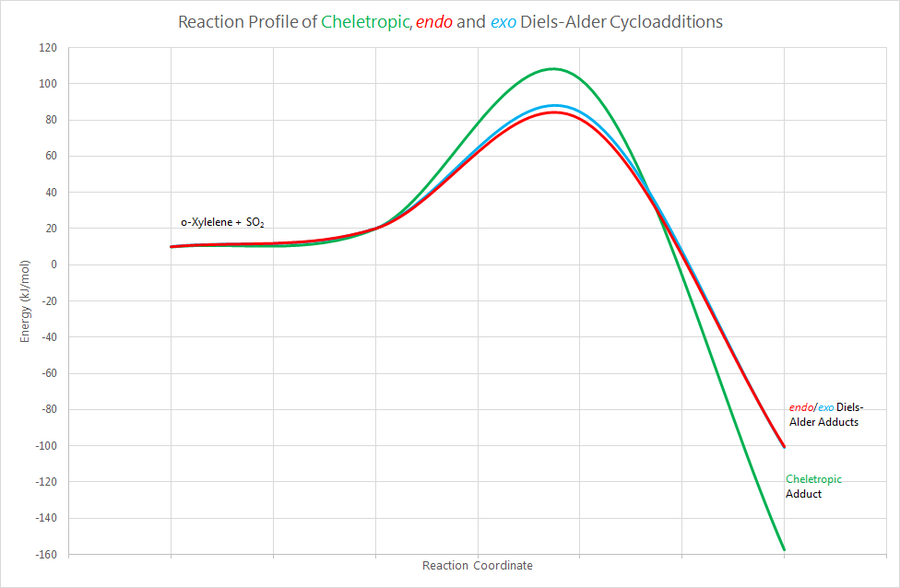
(Where did these curves come from? They are not going to a gradient of 0 at the products. It's much easier to use straight lines Tam10 (talk) 17:15, 10 November 2017 (UTC))

.LOG Uploads

o-Xylylene

Sulphur Dioxide

endo Diels-Alder Adduct

Transition State for endo Diels Alder Adduct

Intrinsic Reaction Coordinate for endoDiels-Alder Adduct

exo Diels-Alder Adduct

Transition State for exo Diels Alder Adduct

Intrinsic Reaction Coordinate for exoDiels-Alder Adduct

Cheletropic Adduct

Transition State for Cheletropic Adduct

Intrinsic Reaction Coordinate for Cheletropic Adduct

Sources

Template loop detected: Template:Reflist

↑ IUPAC. Compendium of Chemical Terminology, 2nd ed. (the "Gold Book"). Compiled by A. D. McNaught and A. Wilkinson. Blackwell Scientific Publications, Oxford (1997). XML on-line corrected version: http://goldbook.iupac.org (2006-) created by M. Nic, J. Jirat, B. Kosata; updates compiled by A. Jenkins. ISBN 0-9678550-9-8. https://doi.org/10.1351/goldbook.

[1] IUPAC. Compendium of Chemical Terminology, 2nd ed. (the "Gold Book"). Compiled by A. D. McNaught and A. Wilkinson. Blackwell Scientific Publications, Oxford (1997). XML on-line corrected version: http://goldbook.iupac.org (2006-) created by M. Nic, J. Jirat, B. Kosata; updates compiled by A. Jenkins. ISBN 0-9678550-9-8. https://doi.org/10.1351/goldbook.

[1]