Rep:Mod:mh3413TS

Gaussian Simulations of Transition States

Abstract

By utilizing the Gaussian platform, the potential energy surface for various molecules were investigated. The potential energy surface corresponds to the total energy of the molecule relative to its geometric configuration. From these different combinations of molecular configurations, the energy maximum and minimum values were able to be found on the energy surface using the stationary points of the system, corresponding to $0=\frac{\partial E(q1)}{\partial q1}$ ie the gradient = 0. q1 is one of the molecular independent 3N-6 nuclear co-ordinates, while E is the energy of the molecule. To establish the properties of the stationary point, the second derivative $k=\frac{{\partial }^{2}E(q1)}{{\partial }^{2}q1}$ was used. When $0>\frac{{\partial }^{2}E(q1)}{{\partial }^{2}q1}$, the stationary point corresponded to the maximum energy on the potential energy surface (the transition state of the reaction), while the $0<\frac{{\partial }^{2}E(q1)}{{\partial }^{2}q1}$ was the minimum energy on the potential energy surface. The transition state produced imaginary frequencies, while the energy minima only observed positive frequencies.

For all the calculations that were undertaken, the molecules were optimized using a PM6 basis set. This is a classical method of approach that does not require an atomic orbital basis set to be defined. The advantage of using this method for the initial calculations, was that it allowed for sensible and fast approximations of the molecular structure using classical mechanics. For exercise 2, the optimized PM6 configurations were further optimized to the B3LYP/6-31G(d) level, which utilizes the more computationally intensive density functional theory method. Relative to experimental values, this method gives good approximations for the thermochemistry of molecular systems, but fails to take into consideration the e- correlation effects.

Nf710 (talk) 22:51, 12 January 2017 (UTC) Maxamimum in that co - ordinate

Bold text==Exercise 1== This is a [4+2] cycloaddition reaction between butadiene and ethlyene, in which there is the addition of the conjugated 4π electron system to a 2π electron system, to produce 2 new sigma-bonds via the dissociation of 2 pi-bonds.

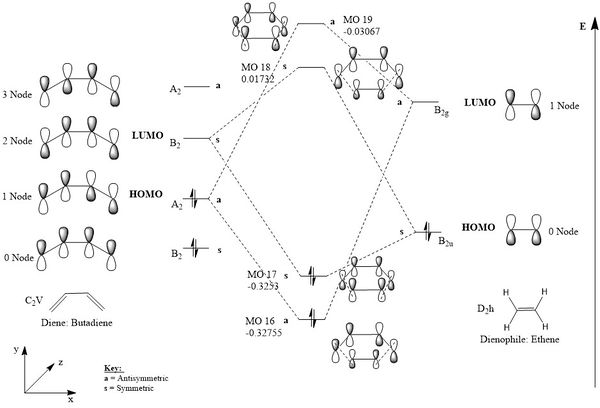
It can be seen below in Figure 1, the energy gap between the HOMO and LUMO orbitals for the ethylene is greater than in the butadiene system. This observation is in line with theoretical observations made from Huckel theory, which concludes the energy levels (HOMO and LUMO energy gap) get closer together, as there is an increase in the pi-conjugation of the system. These results mean that the butadiene molecule would be expected to be more reactive towards nucleophiles than the ethlyene molecule. There is increased stabilization and reactivity in observed in the butadiene system due to the resonance stabilization.

Nf710 (talk) 22:55, 12 January 2017 (UTC) Nice intro, fairly goood understandng you could have spoke about the methods here possibly.

Symmetric - Symmetric & Antisymmetric - Antisymmetric interactions

As the HOMO of the ethylene and the LUMO of the butadiene has MOs with symmetric properties ('s:symmetry label), the interaction between this HOMO-LUMO combination corresponds to a the inverse demand Diels Alder reaction. This would form MO 17(HOMO of Transition State) and MO 18 (LUMO of Transition State) as can be seen in figure 3 and 4. However, as the difference between the MO 16 and MO 17 of the TS is verl, the reaction in theory could favour either the normal (Bold text'a: antisymmetry label interactions creates the HOMO and LUMO) or inverse electron demand reaction. The normal electron demand interaction would be further encouraged by the addition of electron withdrawing groups on the dienophile, which would lower the energy of the LUMO and lead to a better energy match and orbital interactions of the systems. This would consist of the HOMO of the ethylene molecule interacting with the LUMO orbital of the butadiene system. On the other hand, the energy of the HOMO on the diene could equally be increased to match the energy of the LUMO on dienophile by the addition of electron donating groups.

Note: The splitting between the antisymmetric MOs is smaller than the symmetric MOs due to the energy difference being greater between the interacting atomic orbitals.

molecule1
Figure 1: MO diagram correlating the possible combinations of HOMO and LUMO interactions for the symmetric-symmetric and antisymmetric-antisymmetric reactions

Dissecting the MO interactions

Below are the figures of the HOMO and LUMO MOs for the transition state system.

Figure 2: This is the HOMO-1 (MO 16) for the Transition State (ie the a,a bonding interaction)	Figure 3: This is the HOMO (MO 17) for the Transition State (ie the s,s bonding interaction)	Figure 4: This is the LUMO (MO 18) for the Transition State (ie the s,s antibonding interaction)	Figure 5: This is the LUMO+1 (MO 19) for the Transition State (ie the a,a antibonding interaction)

Below are figures of the HOMO and LUMO MOs for the reactants. These computationally generated MOs are in agreement with the theoretically generated MOs in Figure 1.

Figure 6: This is the HOMO for the Butadiene Molecule (MO 11)	Figure 7: This is the LUMO for the Butadiene Molecule (MO 12)

Figure 8: This is the HOMO for the Ethylene Molecule (MO 6)	Figure 9: This is the LUMO for the Ethylene Molecule (MO 7)

Symmetry of the AO interactions

${\mathbf{S}}_{\mathrm{A}\mathrm{B}}=\int {\mathrm{\Psi }}_{\mathrm{A}}^{*}{\mathrm{\Psi }}_{\mathrm{B}}dV$

Only the symmetric-symmetric and antisymmetric-antisymmetric interactions are allowed for this reaction (only the AOs of the same symmetry). The orbital interactions for these symmetry interactions are non-zero. This is due to the quantum mechanical symmetry interactions of the wavefunction for these corresponding orbitals. As shown above, the orbital overlap is product of the orbital wavefunctions of complex conjugate on atom A and the wavefunction on atom B. When the symmetry of these interactions are,

$$\begin{gathered} {\mathbf{S}}_{\mathrm{A}\mathrm{B}}=\int {\mathrm{\Psi }}_{\mathrm{S}\mathrm{y}\mathrm{m}\mathrm{m}\mathrm{e}\mathrm{t}\mathrm{r}\mathrm{i}\mathrm{c}}^{*}{\mathrm{\Psi }}_{\mathrm{A}\mathrm{n}\mathrm{t}\mathrm{i}\mathrm{-}\mathrm{s}\mathrm{y}\mathrm{m}\mathrm{m}\mathrm{e}\mathrm{t}\mathrm{r}\mathrm{i}\mathrm{c}}dV=\int {\mathrm{\Psi }}_{\mathrm{A}\mathrm{n}\mathrm{t}\mathrm{i}\mathrm{-}\mathrm{S}\mathrm{y}\mathrm{m}\mathrm{m}\mathrm{e}\mathrm{t}\mathrm{r}\mathrm{i}\mathrm{c}} \\ =0 \end{gathered}$$

the product of the symmetric and anti-symmetric wavefunctions gives a anti-symmetric wavefunction. This mathematical function integrated over all space would lead to a value of 0, as shown above. Therefore, the orbital overlap between the symmetric and asymmetric orbital systems would be zero. The product of symmetric-symmetric and anti-symmetric-anti-symmetric wavefunctions, would lead to the integration of a symmetric wavefunction. This would result in a value of 1 (when the wavefunctions are normalized) and a non-zero value for the orbital overlap integral.

Nf710 (talk) 23:15, 12 January 2017 (UTC) The integral should be over position

Furthermore, this reaction would not be allowed under thermal conditions according to the Woodward-Hoffman rules as there would be one (4q + 2)s component and one (4r)a component.

Figure 10: This is the transition state vibration -948.7104cm−1	Figure 11: This is the lowest positive frequency vibration 145.0646cm−1

The transition state frequency corresponds to an imaginary frequency (shown as a negative value) due to the force constant of the system being negative. The vibrations combining the reactants is a synchronous process as shown in figure 10. The lowest positive frequency vibration in figure 11, is an vibration that would produce an asynchronous bond formation.

Physical observations of reaction

molecule1
Figure 12: Reaction mechanism with a focus on the transition state

Details of the bond lengths in the reactants, transition structures and product:

Bond (Å)	1	2	3	4	5	6
Starting Materials	1.34	1.47	1.34	1.33	Not Present	Not Present
Transition State	1.38	1.41	1.38	1.38	2.12	2.12
Product	1.50	1.34	1.50	1.54	1.54	1.54
Change in Bond Length	Increase	Decrease	Increase	Increase	Decrease	Decrease

$$\begin{gathered} s{p}^3 \\ to \\ s{p}^3 \\ C-C \\ bond \\ length \\ of \\ product \\ =1.54\dot{A} \end{gathered}$$

$$\begin{gathered} s{p}^3 \\ to \\ s{p}^2 \\ C-C \\ bond \\ length \\ of \\ product \\ =1.50\dot{A} \end{gathered}$$

$$\begin{gathered} s{p}^2 \\ to \\ s{p}^2 \\ C-C \\ bond \\ length \\ of \\ product \\ =1.34\dot{A} \end{gathered}$$

These computed bond lengths are consistent with experimental results.Throughout the reaction the length of bonds 2,5 and 6 decrease, while the bonds 1,3 and 4 increase.

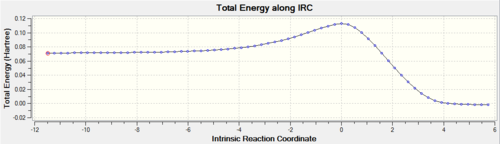
As the reaction commences, the bonds 1,3 and 4 are reduced to a single sigma bond and as a result the bond length increases; reduction in the electron density found between the atoms, reduction in attraction of the two nuclei. As seen in figure 13, bonds 5=6 and bonds 1=3. As the ethylene molecule approaches the butadiene (decrease in the bonds 5 & 6), the bond 4 in the ethylene and bond 1,3 in the butadiene starts to extend in a concerted reaction. Simultaneously, there is a decrease in the length of bond 2 as it starts to develop a pi-bonding system via a [4+2]-cycloaddition reaction. At the transition state, the reaction co-ordinate=0 and the bonds 5 and 6 are substantially larger than a typical sp3-sp3 bond length at 2.12Å. Upon the equilibration of the bond lengths in the product structure, there are deviations seen in the single sigma bond lengths. These correspond to the sp3-sp2 C-C bonds, which still contains a small amount of pi-bonding character from the neighboring pi-bond, leading to a slight decrease in the bond length.

At the Transition State:

$$\begin{gathered} Total \\ C-C \\ bond \\ length \\ at \\ the \\ Transition \\ State \\ = \\ Van \\ der \\ Waals \\ radii \\ + \\ C-C \\ (sp3-sp3) \\ bond \\ length \end{gathered}$$

As:

$$\begin{gathered} Total \\ C-C \\ bond \\ length \\ at \\ the \\ Transition \\ State \\ =2.12\dot{A} \end{gathered}$$

$$\begin{gathered} C-C \\ (sp3-sp3) \\ bond \\ length \\ =1.54\dot{A} \end{gathered}$$

$$\begin{gathered} 2.12\dot{A} \\ = \\ Van \\ der \\ Waals \\ radii \\ + \\ 1.54\dot{A} \end{gathered}$$

$$\begin{gathered} Van \\ der \\ Waals \\ radii \\ = \\ 0.757\dot{A} \end{gathered}$$

molecule1	molecule1
Figure 13: Plot of the change in the bond length with respect to the reaction co-ordinate	Figure 14: IRC of the reaction mechanism

Exercise 2

molecule1
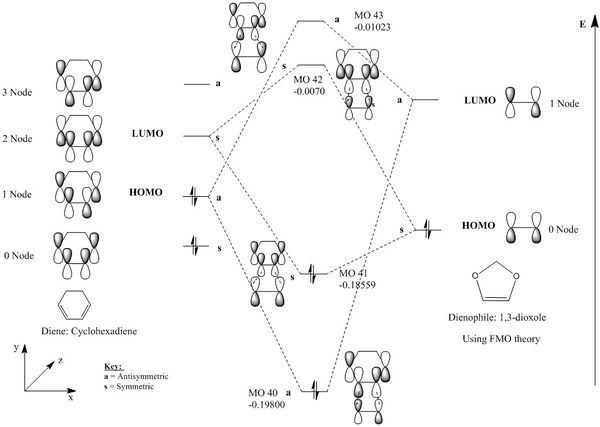
Figure 15: MO diagram correlating the possible combinations of HOMO and LUMO interactions for the symmetric-symmetric and antisymmetric-antisymmetric reactions

This reaction is similar to the reaction above as it is a [4+2] cycloaddition, except the 1,3-Dioxole dienophile contains oxygen atoms in the ring structure, causing them to act as EWGs. This would lower the energies of the HOMO and LUMO for the dienophile molecule relative to the ethylene molecule mentioned in the exercise above, and encourage the reaction to proceed via a Diels-Alder reaction. This reaction is regioselective and therefore can produce two products; EXO where the oxygen groups are point away from the diene, or the ENDO structure where the oxygen groups are pointing towards the diene ring structure.

(In dioxole, these oxygens can be treated as R-O- groups which are EDGs Tam10 (talk) 12:03, 3 January 2017 (UTC))

The TS frequency recorded for the:

Product (cm-1)	TS ENDO PM6	TS ENDO B3LYP	TS EXO PM6	TS EXO B3LYP
Transition State	-936.05	-520.94	-959.61	-528.60

There were no imaginary frequencies recorded for the reactants or the product systems and the log files indicated the convergence of the energies. This confirmed the reactants and products were at an minimum energy state on the potential energy surface. The HOMO and LUMOs of the Transition states for both the ENDO and EXO products were observed to be symmetric. The symmetric HOMO and LUMO MOs indicates an inverse electron demand Diels–Alder reaction; reaction between the higher energy LUMO of the diene, with the HOMO of the dienophile. The smaller energy splitting of the symmetric-symmetric MOs relative to the antisymmetric-antisymmetric interactions, is due to the Cyclohexadiene LUMO and 1,3-Dioxole HOMO being further apart in energy than the normal demand Diels Alder reaction.

Symmetry of the AO interactions

Figure 16: Symmetrical Endo Transition State Bonding MO 41 (HOMO)	Figure 17: Symmetrical Endo Transition State Anti-Bonding MO 42 (LUMO)

Figure 18: Symmetrical Exo Transition State Bonding MO 41 (HOMO)	Figure 19: Symmetrical Exo Transition State Anti-Bonding MO 42 (LUMO)

(The HOMO-1 and LUMO+1 for each are also important, as you have shown in the MO diagram above Tam10 (talk) 12:03, 3 January 2017 (UTC))

Species (kJ/mol)	ENDO Product	EXO Product
Reactants	-1.31377996E+06	-1.31377996E+06
Transition State	-1.31362185E+06	-1.31361399E+06
Product	-1.31385254E+06	-1.31384546E+06
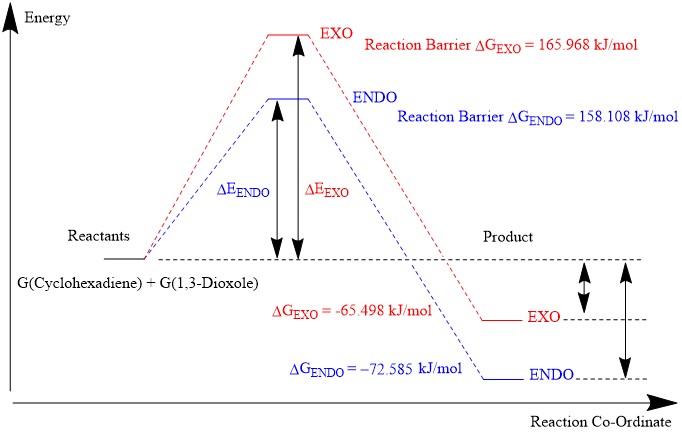
Reaction Energy Barrier	158.1075871	165.9683329
Change in Energy	-72.58456249	-65.49833902

In general it would be expected that the Diels-Alder reaction would produce:

Thermodynamic Product = EXO Product - Higher reaction barrier - Lower energy product

Kinetic Product = ENDO Product - Lower reaction barrier - Higher energy product

However, in this reaction, it was found that the ENDO product is the kinetic product (the product with the lowest reaction barrier) and the thermodynamic product (the product with the lowest energy). This result is not uncommon as several other computational studies on the [4+2] Diels-Alder reaction have reported similar results. For all the calculations undertaken, the molecules were optimized using a PM6 basis set and then to the B3LYP/6-31G(d) level. As the Gibbs free energy is a state function, the total Gibbs free energy of the reactants was found by:

molecule1
Figure 20: Reaction profile energies for the computed reaction

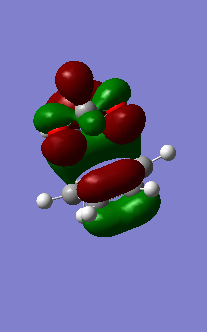
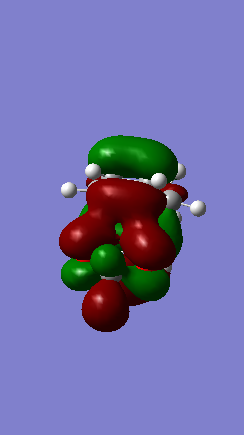
Secondary orbital interactions

One of the reasons that the ENDO product mechanism possesses a lower reaction barrier is due to the secondary orbital that is possible as seen in figure 20-22. Different isovalues have been used to show the transition state interactions with the corresponding atoms. In Figure 20, it can be clearly seen that the stabilizing interactions occur between the out of plane p-orbital (containing the lone pair) on the electron withdrawing oxygen atoms and the p-orbitals involved in the formation of the newly formed pi-bond. The interaction between these orbitals is not significant enough to change the course of the mechanism and form a new bond, but would lead to a lowering of the ENDO transition state and lead to the ENDO product being the favoured kinetic product.

Sterics between the approaching two molecules also contributes to the final reaction barrier observed. In general the ENDO product is more congested and thus has a higher steric contribution than in the EXO product.

molecule1	molecule1	molecule1
Figure 21: Transition State HOMO (MO 41) of the reaction, corresponding to isovalue =0.05	Figure 22: Transition State HOMO (MO 41) of the reaction, corresponding to isovalue =0.02	Figure 23: Transition State HOMO (MO 41) of the reaction, corresponding to isovalue =0.01

Nf710 (talk) 23:35, 12 January 2017 (UTC) more sterics would mean more unstable exo, but it isnt...

Exercise 3

This reaction involved the calculations of the [4+2] o-Xylylene-SO2 cycloaddition and the [4+1] cheletropic product at the PM6 level.

Formation of the ENDO product

molecule1	molecule1	molecule1
Figure 24: Reactants in the Diels-Alder ENDO product reaction	Figure 25: Transition state of the Diels-Alder ENDO product reaction	Figure 26: Products of the Diels-Alder ENDO product reaction

Figure 27: IRC of the Diels-Alder ENDO product reaction

Formation of the EXO product

molecule1	molecule1	molecule1
Figure 28: Reactants in the Diels-Alder EXO product reaction	Figure 29: Transition state of the Diels-Alder EXO product reaction	Figure 30: Products of the Diels-Alder EXO product reaction

Figure 31: IRC of the Diels-Alder EXO product reaction

Formation of the Cheletropic product

molecule1	molecule1	molecule1
Figure 32: Reactants in the Cheletropic reaction	Figure 33: Transition state of the Cheletropic reaction	Figure 34: Products of the Cheletropic reaction

Figure 35: IRC of the Cheletropic reaction

Species (kJ/mol)	ENDO Product	EXO Product	Cheletropic Product
Reactants	157.6507502	157.6507502	157.6507502
Transition State	237.7626201	241.7481285	260.0898689
Product	56.96021426	56.32746885	-0.005250999
Reaction Energy Barrier	80.11186991	84.09737833	102.4391187
Change in Energy	-100.6905359	-101.3232813	-157.6560012

This reaction was similar to the reaction in exercise 2. In this reaction, the ENDO product was found to be the kinetic product as it had the smallest reaction barrier to the achieve the transition state structure. Under kinetic conditions ie minimal temperature, the ENDO product would be the major product formed in the irreversible reaction. The EXO product has a higher reaction barrier relative to the ENDO product, as the SO2 moelcule approaches the diene with the oxygens in a planar orientation, leading to an increase in the steric interactions with the hydrogens. This does not occur for the ENDO product as one of the oxygens are pointing out from the ring.

The cheletropic product has the highest reaction barrier of the reaction, but also is the most thermodynamically stable product. This reaction has a transition state in which the cyclic diene system is interacting with the sulphur atom. The product results in the formation of a 5 membered ring system with the loss of an alkene bond and the formation of two sigma bonds. There is an increase in the co-ordination number of the sulfur.

It can be seen in the IRCs gif figures 27,31 and 35, over the course of the reaction, the cycloaddition reactions are stabilised by the aromatisation of the 6 membered ring system in the product. This produces a very strong driving force for all of the products.

The ENDO and EXO products are formed through a Diels Alder like [4+2] cycloaddition reaction with heteroatoms, while the cheletropic product is formed from a [4+1] cycloaddition reaction. The cheletropic product is more stable due to the formation of a more stable ring adduct. Under sufficient high energy conditions (high temperatures), the reaction would become under thermodynamic control and in equilibrium. Eventually, all the reactants would be driven to the most stable cheletropic product. This illustrates that in a reactions mixture, such as in the o-Xylylene-SO2 Cycloaddition reaction, there are competing mechanisms occur.

molecule1
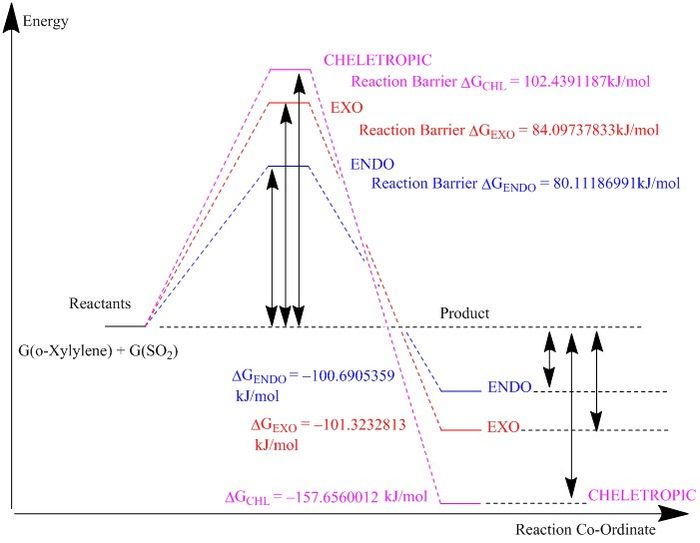Figure 36: Reaction profile energies for the computed reaction