Rep:Mod:mga2601
Module 3: Physical
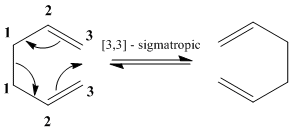
The Cope Rearrangement
1,5-Hexadiene undergoes a concerted [3,3] sigmatropic rearrangement, known as the Cope rearrangement, proceeding via either a 'chair' or 'boat' transition state.
- Can quantum mechanics be used to isolate the transition states involved in the reaction?
- Can the activation energies for the reaction be predicted?
Optimising the reactant molecule
Use of the HF/3-21G method/basis set, and manually changing the pre-optimised structures into either a guache or anti conformation, enabled a number of the minimum energy conformations of 1,5- Hexadiene to be found.
Optimisation of an 'anti' starting conformation, led to the ANTI 1 (as referred to in appendix 1)conformation being obtained. The optimisation, therefore, successfully isolated the minimum energy anti conformation.
| Conformation | |
| Point Group | C2 |
| Energy/ a.u. | -231.69260 |
http://neon-tmp.cc.ic.ac.uk/wiki/images/b/b8/Anti_1_Opt.txt
In contrast, optimisation of an initial gauche starting conformation led to the isolation of GAUCHE 1, not the lowest energy conformation, gauche 3, possibly beacause the starting conformation was too far away from the lowest energy confromation. Clearly the gauche 1 conformation is higher in energy than the anti 1 conformation, as would be expected given the greater degree of steric interaction, particulary between the terminal ends of the carbon chain.
| Conformation | |
| Point Group | C2 |
| Energy/ a.u. | -231.68772 |
http://neon-tmp.cc.ic.ac.uk/wiki/images/b/b3/Gauche_1.txt
Based on this, it should be expected that by reducing this steric clash, through altering the relative conformations of the two double bonds, a lower energy gauche conformation could be found.
Manually changing the conformation of the above gauche 1, so that the two double bonds are 'pointing out' (rather than'in'), hence reducing the steric clash, followed by re-optimisation led to the isolation of GUACHE 4, lower in energy, albeit still not the global minimum conformation.
| Conformation | |
| Point Group | C2 |
| Energy/ a.u. | -231.69153 |
http://neon-tmp.cc.ic.ac.uk/wiki/images/0/04/Gauche_4_opt.txt
Only upon further optimisation was the minimum energy conformation, GAUCHE 3, obtained.
| Conformation | |
| Point Group | C1 |
| Energy/ a.u. | -231.69266 |
http://neon-tmp.cc.ic.ac.uk/wiki/images/b/bf/Gauche_3.txt
Optimisation of the anti 2 reactant conformation
The anti 2 conformation was initially found using the HF/3-21G method and basis set.
| Conformation | |
| Point Group | Ci |
| Energy/ a.u. | -231.69254 |
http://neon-tmp.cc.ic.ac.uk/wiki/images/3/3f/Anti_2_HF_Opt.txt
This structure was then further optimised using a higher level of theory: DFT B3LYP method with the 6-31G(d) basis set.
| Conformation | |
| Point Group | Ci |
| Energy/ a.u. | -234.61172 |
http://neon-tmp.cc.ic.ac.uk/wiki/images/9/9a/Anti_2_DFT_Opt.txt
| Bond | HF r/Å | DFT r/Å | Angle | HF /° | DFT/° | Dihedral angle | HF/° | DFT/° |
|---|---|---|---|---|---|---|---|---|
| C1=C2 | 1.316 | 1.333 | C1-C2-C3 | 124.8 | 125.3 | C1-C2-C3-C4 | -114.7 | -118.5 |
| C2-C3 | 1.509 | 1.504 | C2-C3-C4 | 111.3 | 112.6 | C2-C3-C4-C5 | 180.0 | 180.0 |
| C3-C4 | 1.553 | 1.549 | C3-C4-C5 | 111.3 | 112.6 | C3-C4-C5-C6 | 114.7 | 118.5 |
| C4-C5 | 1.509 | 1.504 | C4-C5-C6 | 124.8 | 125.3 | |||
| C5-C6 | 1.316 | 1.333 |
As table 1 demonstrates, the differences in the geometry between the methods is not highly significant. However, without comparison to experimental values it is difficult to ascertain which method is the accurate.
Frequency calculation for anti 2
| Energy/ Hartrees | |
|---|---|
| Sum of electronic and zero point energies (0K) | -234.469181 |
| Sum of electronic and thermal energies (298K) | -234.461839 |
| Sum of electronic and thermal enthalpies | -234.460895 |
| Sum of electronic and thermal free energies | -234.500745 |
http://neon-tmp.cc.ic.ac.uk/wiki/images/9/9a/Anti_2_DFT_freq.txt
- As expected, the energy of the molecule at 298K is higher than at 0K. This is due to kinetic energy contributions to the energy (eg. rotational,vibrational and translational degrees of freedom).
- From comparison of the energy and enthalpy at room temperature, the amount of available thermal energy can be found (H=E + RT) eg. (-234.460895 - -234.461839 = 9.44x10-4 hartree. Since 1H = 2625.5kJmol-1, ΔE = 2.478kJmol-1 (3dp). Comparison to RT (8.314 JK-1mol-1 x 298K = 2.478 kJmol-1, shows this to be correct).
Optimisation of the 'Chair' and 'Boat' Transtion Structures
File:Allylfragment.gif The 6- member transition state involved in the Cope rearrangement is believed to proceed via either a boat or chair like conformation. There are several quantum mechanical based methods that can be used to optimise these transition states. Three different methods have been utilised here.
a. Optimisation of the 'chair' transtion structure: Method 1 - calculation of the force constants at the start of the calculation
After the initial optimisation of an allyl fragment, two of these fragments were combined in a way that best represented a possible chair transtion state. The distance between the terminal ends of the two fragments was set to be as close to 2.2Å as possible - this structure represents the initial 'guess' at the chair transtion structure.
b. The guess transition state from above was optimimised (Opt+Freq using the HF/3-21G basis set) to a 'TS Berny' using Guassian. This optimisation is achieved through computation of the Hessian, initially, at the start of the optimisation.
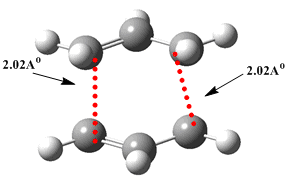
The optimised structure clearly does correspond to a 'chair' like 6 - member transition state. The frequency analysis confirms this, the imaginary frequency of - 818 cm-1 corresponding to the transition state. eg. a negative frequency equates to a maxima on the PES. Hence, a transtion state has been successfully isolated. Upon animation of the -818cm-1 vibration, it can be seen that this clearly corresponds to the Cope rearrangemet e.g. as one bond 'forms' (distance between two terminal ends decreases), another bond 'breaks' (distance between the two terminal ends increases).
http://neon-tmp.cc.ic.ac.uk/wiki/images/4/44/Chair_trans_1.txt
c. Optimisation of the chair transition structure: Method 2 - use of the Redundant Coordinate Editor Again using the 'guess' chair transition state structure, the redundant coordinate editor was now employed to 'freeze' both of the terminal carbon distances, between the two sets of C-C involved in bond formation and breaking, to 2.2Å. This was then optimised to a minimum (HF/ 3-21G) yielding a chair like TS structure with the distance between the two sets of terminal carbons now set to 2.2Å, in contrast to the final optimised TS structure from part b, where this distance was 2.02Å.
d. The second step of this method, to optimise the chair transition structure, required Gaussian to differentiate along the reaction coordinate with the terminal C-C distances previously frozen in part c, now 'unfrozen'. The resulting structure corresponded to that found in part b, with an imaginary frequency of -818cm-1 and terminal C-C distances of 2.02Å.
http://neon-tmp.cc.ic.ac.uk/wiki/images/6/62/Chair_trans_from_frozen_coord.txt
Hence, both methods have been successful in isolating the 'chair' transition structure of 1,5 hexadiene in the Cope rearrangement.
e. Optimisation of the boat transition structure: Method 3 - QST2
Two anti 2 1,5 - hexadiene molecules were labelled such that the atoms in the one designated the 'product' correlated to those found in the 'reactant' had the Cope rearrangement taken place.
| File:Labelledprod react.gif |
The QST2 method takes these two input structures and interpolates between them to find the correct transition structure. However, upon initial optimisation to a TS (QST2) using these initial geometries, the calculation was not successful. Instead of returning a boat transition state, it gives a distorted chair structure (with terminal C-C distances of 3.12Å) . This indicates that the starting geometries used to perform this optimisation were not close enough to that of the boat transtion structure for the interpolation (to the boat TS) to be successful.
http://neon-tmp.cc.ic.ac.uk/wiki/images/f/fa/BOAT_shouldfail.txt
Hence, the reactant and product geometries needed to be altered in a way, such that the boat transtion state could be isolated. The following adjustments being made for both the product and reactant:
- Central dihedral angle, C7-C4-C1-C9 (or C7-C14-C11-C9 for product) altered to 0°.
- The internal C7-C4-C1 and C4-C1-C9 angles (or C7-C14-C11/ C14-C11-C4 for product) altered to 100°.
 |
A second Opt+Freq calculation to the TS(QST2) was performed, successfully obtaining the boat TS, as shown by an analysis of the frequency calculation. Only one imaginary frequency, of -840cm-1, was found, indicating the isolation of a maxima. As with the chair TS case, the animation of this imaginary vibration, indicates that it does correspond to the Cope rearrangement - eg. concerted bond formation/ bond breaking as indicated by the concerted C-C bond length decrease/increase respectively.
http://neon-tmp.cc.ic.ac.uk/wiki/images/1/1f/BOAT_success.txt
The Intrinsic Reaction Coordinate (IRC)
f. Use of the IRC method enables the product conformation of 1,5 hexadiene to be found w.r.t the TS. This is achieved through Guassian following the minimum energy pathway from the maxima (transtion state) to a local minimum.
An initial IRC calculation was performed on the chair transition state, found through optimisation using HF/3-21G theory in part b.
| Parameter | |
|---|---|
| Direction | Forward only |
| Compute Force Const. | Once |
| N | 50 |
Upon viewing the results it was clear that the IRC method had not succeeded in isolating a minimum on the PES. The sturcture obtained did not correspond to any of the minimum energy conformations of 1,5- hexadiene as listed in Appendix 1 [1] and with an energy of -231.68043 Hartrees, suggests that a minimum was not found . This can be confirmed by viewing the RMS gradient of the PES (eg. the 1st derivatie of the PES), which clearly shows that a stationary point on the PES has not been isolated upon following the PES away from the TS.
There are three sugested methods that could be used to attempt to improve upon this initial failure and successfully locate a minimum energy product conformation.
- Method iii.: Compute the force constants at every step: DOI:10042/to-4732
-More time consuming and therefore costly in terms of computational expense, but reported to be the most reliable.
| Parameter | |
|---|---|
| Direction | Forward only |
| Compute Force Const. | Always |
| N | 50 |
Comparison of the structure isolated using method iii. with the known minimum energy conformations of 1,5 hexadiene reveals that a guache 2 conformation (with E= -269.69166 Hartree) has been found . However, although this is a minimum energy conformation, it is not the lowest enegy conformation (eg. gauche 3) that is possible. Hence, although the IRC calculation has successfuly isolated a minimum (see RMS gradient plot) on the PES, it has found a local rather than the global minimum.
How does method iii. compare to the other two possible methods?
- Method i.:Optimise the final structure obtained from the initial IRC calculation, to a minimum. DOI:10042/to-4733
As with method iii, use of method i. returned a guache 2 minimum energy conformation (E=-231.69167 Hartree) , albeit in a much faster time (although not necesseraly completely indicative of relative complcation of job as reported SCAN times also dependent on number of jobs running etc.).
- Method ii.: Compute a larger number of points along the IRC DOI:10042/to-4734
Increasing the number of steps along the IRC succesfully enabled a minimum energy conformation to be found, albeit not all these steps were required, with the guache 2 structure having been isolated at N=56, . Hence, it would seem that only another 5 steps, corresponding to a 0.002 Hartree energy difference, was required, w.r.t the initial IRC calculation, in order to find a minimum.
| Parameter | |
|---|---|
| Direction | Forward only |
| Compute Force Const. | Once |
| N | 100 |
Overall, all three methods employed successfully managed to find a local minimum energy conformation. Given that all methods returned a guache 2 conformation, as opposed to the global minimum energy conformation, it would seem reasonable to suggest that use of mehtod 1, in this instance, based on the speed of the calclulation, would be the most practical method.
- Can the IRC method be applied to the boat transtion structure?
An IRC calculation was initially run with N=50 and calculating force constants at each step (eg. method iii as applied to the chair T). This was unsuccessful in locating a known minimum energy structure. Hence, the number of steps in the IRC calculation was increased up to 70 - having no effect on the outcome.
Nevertheless, by using a higher level basis set and increasing N = 150, the lowest possible energy conformation, guache 3, was obtained .
| Attempt | N | Energy/ Hartree | Method/ Basis set | DOI |
|---|---|---|---|---|
| 1 | 50 | -231.68303 | HF/3-21G | DOI:10042/to-4740 |
| 2 | 60 | -231.68303 | HF/3-21G | DOI:10042/to-4739 |
| 3 | 70 | -231.68303 | HF/3-21G | DOI:10042/to-4738 |
| 4 | 150 | -234.61131 | B3LYP/6-31G (d) | DOI:10042/to-4737 |
It is clearly slightly more difficult to obtain a minimum on the PES, using the IRC method, when applied to a boat TS rather than a chair TS. This perhaps indicates that the boat TS is further away from a minimum energy structure the chair TS.
Activation Energies and Optimisation at a Higher Theory Level
Using a higher level of theory (DFT/B3LYP/6-31G(d)), the HF/3-21G optimised transition states were re-optimised. Comparison of the geometries between the two levels of theory shows very little difference between the two. The higher level theory should be more accurate, hence, as they show such similarity, use of the lower level theory to approximate the geometry is justified.
| Parameter | Chair (HF/3-21G) | Chair (B3LYP/6-31G)DOI:10042/to-4741 | Boat (HF/3-21G) | Boat (B3LYP/6-31G)DOI:10042/to-4742 |
|---|---|---|---|---|
| Inter allyl fragment distance /Å | 2.02 | 1.97 | 2.14 | 2.21 |
| C-C-C angle /° | 120.5 | 120.0 | 121.7 | 122.3 |
| r(C-C) /Å | 1.39 | 1.41 | 1.38 | 1.39 |
- How do the thermochemistry properties compare?
| HF/3-21G | B3LYP/6-31G (d) | ||||||
|---|---|---|---|---|---|---|---|
| Structure | Electronic Energy | Σ electronic + zero point energies (0K) | Σ electronic + thermal energies (298K) | Electronic Energy | Σ electronic + zero point energies (0K) | Σ electronic + thermal energies (298K) | |
| Reactant (anti 2 conformation) | -231.692535 | -231.539539 | -231.532566 | -234.611720 | -234.469181 | -234.461839 | |
| Chair transition state | -231.619322 | -231.466699 | -231.461340 | -234.556983 | -234.414930 | -234.409009 | |
| Boat transition state | -231.602802 | -231.450929 | -231.445299 | -234.543093 | -234.402342 | -234.396008 |
Calculation of the activation energies shows that there is quite a significant difference between the values obtained from the two different levels of theory. Not surprisingly, the higher level of theory shows a much better agreement to the given experimental values [2], although still just outside the error limit of the experimental data. Nevertheless, the computational methods employed do provide a good way of understanding the Cope rearrangment.
- Both methods correctly predict that the boat TS is higher in energy than the chair TS. This is to be expected, based on the fact that the chair conformation is much less eclipsed in nature.
- On average the difference between the activation energy calculated from HF/3-21G is 12.59 kcalmol-1 higher in energy than the B3LYP/6-31G equivalent. In contrast, the relative difference between the two theories in terms of the average energy difference between the boat and chair TS is only ~1.8 kcalmol-1.
- Both methods indicate that at room temperature, the barrier from reactant to TS is lower than at 0K. Looking at the above table indicates that temperature has a more significant effect on the relative energy of the transition states rather than the reactant energy.
- The relative enrgies of the states at 298K are higher in energy than those at 0K - as would be expected, given that at this higher temperature, the molecules have more accessible degrees of freedom (e.g. includes kinetic energy terms).
| HF/3-21G | HF/3-21G | B3LYP/6-31G(d) | B3LYP/6-31G(d) | |
|---|---|---|---|---|
| Temperature | 0K | 298K | 0K | 298K |
| Chair ΔE /kcal mol-1 | 45.71 | 44.69 | 34.04 | 33.15 |
| Boat ΔE/ kcal mol-1 | 55.60 | 54.76 | 41.94 | 41.31
|