Rep:Mod:mg5715TS

Introduction

Potential energy surface

Fig.1 The potential energy curve of a diatomic molecule

The potential energy surface of a diatomic molecule is anharmonic oscillation (as shown in Fig.1). The lowest point in this energy potential is a stationary point, which means it has a zero first derivative:

$\frac{dE(R)}{dR}=0$ Equation 1. First derivative of 1-D potential energy

R stands for the bond length and the physical meaning of the first derivative of potential energy is the force acting on the atoms and the second derivative is the force constant (k). The bond will vibrate; so the vibration wavenumber could be calculated by Equation 2.

$\tilde{v}=\frac{1}{2c\pi }\sqrt{\frac{k}{\mu }}$ Equation 2. Vibrational wavenumber of a diatomic molecule

where $\mu$ is the reduced mass and it could be calculated by Equation 3.

$\mu =\frac{M_A{M}_B}{M_A+M_B}$ Equation 3. Reduced mass of a diatomic molecule

Fig.3 Potential energy surface of triatomic molecule

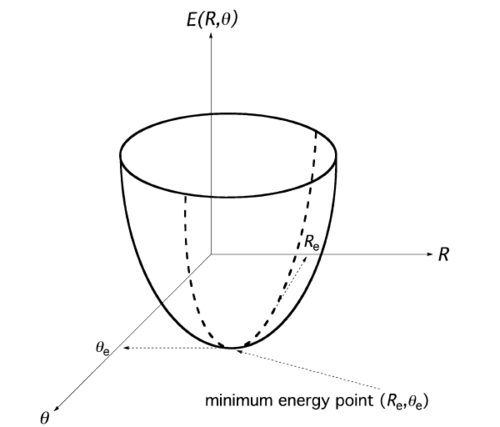
For a triatomic molecule (e.g.H₂O), the potential energy surface has two coordinates including bond length R and bond angle $\theta$ and the potential energy surface is shown in Fig.3. For a non-linear molecule including N atoms, it will have 3N-6 independent geometric variables. For each atom, it will have three variables (bond length, bond angle and torsional angles).The three global rotations and three global translations should be subtracted, so it has 3N-6 degrees of freedom. If it is a linear molecule, there only have two rotation axes, so it has 3N-5 independent geometric variables. A stationary point of the potential energy surface, which has 3N-6 degrees of freedom, could be defined by equation 4.

Nf710 (talk) 19:30, 28 March 2018 (BST) You have nicely introduced the concept of why we use degrees of freedom. Well done.

$\frac{dE(\mathbf{R})}{d{R}_i}=0i=1,2,3,...3N-6$ Equation 4. General equation of a stationary point with 3N-6 variables

where R is the set of all nuclear coordiantes.

Fig.4 The 1-D potential energy surface of a reaction

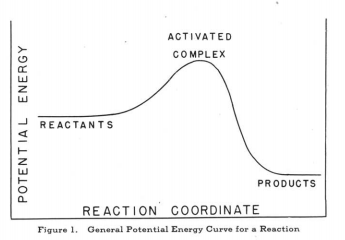
Fig.4 is a 1-D potential energy surface of a reaction. Products and reactants are the minimum points on the lowest energy pathway. For transition state, it is the maximum point on the lowest energy pathway. All of reactants, products and transition state are the stationary points, which means that they satisfy this equation: ($\frac{dE(\mathbf{R})}{dR}=0$). The second derivative of potential energy surface, the force constant, is used to distinguish the products and reactants with the transition state. Reactants and products are minima , so the second derivative is positive.($\frac{d^{2}E(\mathbf{R})}{d{R}^2}>0$) Transition state is the saddle point

of the potential energy surface, which means its second derivative is negative.($\frac{d^{2}E(\mathbf{R})}{d{R}^2}<0$) The force constant of transition state is negative; so, the vibration wavenumber will be imaginary at transition state according to Equation 2.

Nf710 (talk) 19:30, 28 March 2018 (BST) Almost there, but the second derivatives wrt to the degrees of freedom need to be put into the hessian matrix and then diagonalised. And it is the eigenvalues which give you the force constants. And the eigen values are linear combinations of the degrees of freedom. hence why when you move back and forth along this vector it looks like a vibration.

Approximations

The time-independent Schrödinger equation is:

$\hat{H}{\mathrm{\Psi }}_A=E{\mathrm{\Psi }}_A$ Equation 5. Time-independent Schrödinger equation

where $\hat{H}$ is an operator called Hamiltonian, ${\mathrm{\Psi }}_A$ is the wavefunction of electron A, and E stands for the energy. Schrödinger equation could be rewritten by Dirac notation ($\hat{H}|\mathrm{\Psi }=E|\mathrm{\Psi }$).Premultiply the complex conjugation of the wavefunction and integrate over all variables and then rearrange the equation, an euqation of E will be gained. ($E=\frac{<{\mathrm{\Psi }}^{*}|\hat{H}|\mathrm{\Psi }>}{<{\mathrm{\Psi }}^{*}|\mathrm{\Psi }>}$) where the denominator is the overlap integer. If the wavefunction is normalised, the overlap integer should be 1; so $E=<{\mathrm{\Psi }}^{*}|\hat{H}|\mathrm{\Psi }>$.

The Hamiltonian operator for a molecule could be separated into kinetic and potential energies of individual particles ($\hat{E}={\hat{T}}_n+{\hat{T}}_e+{\hat{V}}_{ee}+{\hat{V}}_{en}+{\hat{V}}_{nn}$).T stands for the kinetic energy and V is the potential energy.The Born-Oppenheimer approximation

is the first key approximation for Schrödinger equation. Because the motion of electrons is much faster than that of nuclei, the kinetic energy of the nucleus could be ignored and the potential energy of nuclei's interaction will be constant. Hence, the Hamiltonian operator could be rewritten to ${\hat{E}}_{BO}=+{\hat{T}}_e+{\hat{V}}_{ee}+{\hat{V}}_{en}+constant$

In quantum chemistry, another very important approximation is that the wavefunction of a molecule is the linear combination of atomic orbitals (LCAO)

as shown in Equation 6.

$\mathrm{\Psi }(r)=\sum _n^N{c}_n{\varphi }_n(r)$ Equation 6. linear combination of atomic orbitals

where ${\varphi }_n(r)$ is the basis set (atomic orbital). Therefore the hamiltonian could be rewriten as Equation 7.

$E=<{\mathrm{\Psi }}^{*}|\hat{H}|\mathrm{\Psi }>=\sum _n^N\sum _m^N{c}_m<{\varphi }_m(r)|{\varphi }_n(r)>c_n$ Equation 7. linear combination of atomic orbitals

The more basis sets are used, the more accurate the molcular orbital is, but increasing the basis sets will increase the cost of computational effort.

Nf710 (talk) 19:30, 28 March 2018 (BST) And then this can be written as a matrix which can be diagonalised to get the energy. The degree of how difficult the diagonalisation is due to size etc or approximations governs the speed of the method.

Computational Methods

Although Gauss View contains lots of different calculation method, only two of them are used in this lab: (1) Semi-empirical method PM6 and (2) Density Functional Theory(DFT) method B3LYP.

The Semi-empirical method is based on the experimental data, which will save time for calculating. The density functional theory is the calculation based on theory and does not include any experimental data. Therefore, this process is slower than semi-empirical method.

Methods to find Transition State

• Method 1

(1) predict and draw a guess transition state structure

(2) optimise the guess transition state structure to TS(Berny) and set Calculate force constants to once and the output is the optimised transition state (Only have one imaginary frequency)

This method is quite easy and it is the fastest method.However, this method is not very reliable and it only works for small systems because it will fail easily if the predicted transition state is not close to the real transition state.

• Method 2

(1) predict and draw a guess transition state structure

(2) freeze the distance between atoms where the bond will be formed in the reaction

(3) optimise the frozen-bond structure to a minimum

(4) repeat method 1(2)

This method is similar to method 1 but this one is more reliable than method 1 because it freezes the atoms to prevent them from moving. This makes sure the system close to the transition state before calculation. However, this also will fail easily.

• Method 3

(1) draw the reactant(s) or product(s) and choose the one which has fewer molecules.

(2) optimise the reactant(s) or product(s) to a minimum

(3) break or form the bond and freeze the distance between atoms

(4) repeat method 2 (2)-(4)

This method is much more reliable than the previous two methods and it does not need to predict the possible transition state. However, this method is more complicated and it requires more steps.

Nf710 (talk) 19:30, 28 March 2018 (BST) This was a good section. You had a good attempt at explaining the quantum chemistry.

Excercise 1: Reaction of Butadiene with Ethylene

Fig.5 The reaction scheme of cycloaddition of butadiene and ethylene

The reaction of butadiene with ethylene is a traditional [4+2] cycloaddition, which also known as Diels-Alder reaction.In Diels-Alder reaction, a conjugated diene (butadiene) will react with a dienophile (ethylene) to form a cyclohexene and the reaction scheme is shown in Fig 5. Although the s-trans conformation is more energetically favourable, the conformation of diene should be s-cis because of the interaction between the frontier molecular orbitals(FMO). Moreover, the energy barrier between s-trans and s-cis is not extremely high. In this exercise, all reactants, products and transition state were optimised by semi-empirical method PM6

in Gauss View and Method 2
is used to locate the transition state. 

MO analysis

Fig.6 The molecular orbital of cycloaddition of butadiene with ethylene

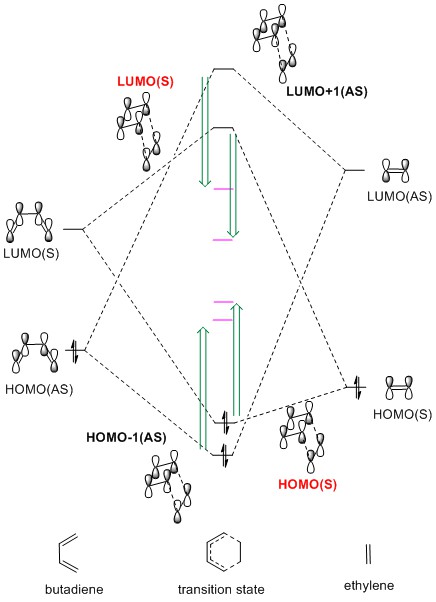
The MO diagram is shown in Fig.6 and this graph is drawn according to the energy calculated by PM6. The energy of product (black

line) should be lower than that of the reactants, and the energy of transition state (pink
line) is higher than that of reactants. The HOMO and LUMO are shown in Table 1. 

Table 1. The HOMO and LUMO diagram of reactants, product and transition state

	Butadiene	Ethylene	MO of Transition State
LUMO			LUMO of Transition State	LUMO+1 of Transition State
HOMO			HOMO of Transition State	HOMO-1 of Transition State

For a [p+q]-cycloaddtion reaction, it could be driven either thermally or photochemically. For photochemical reaction, the electrons on HOMO will be excited to LUMO and become two SOMOs.Therefore, the photochemical cycloaddition is a little bit different with the thermal cycloaddition. A general rule called Woodward Hoffmann Rule is used to determine whether the cycloaddition is allowed or forbidden.

• Woodward-Hoffmann Rule for cycloaddition reactions

For a [p+q]-cylcoaddtion reaction, only two components are involved, where one contains p π-electrons and the other one has q π-electrons. s stands for suprafacial and a means antarafacial

Table 2. Woodward-Hoffman Rule

p+q	Thermally allowed	Photochemically allowed
4n	ps+qa or pa+qs	ps+qs or pa+qa
4n+2	ps+qs or pa+qa	ps+qa or pa+qs

In this reaction, butadiene has 4 π-electrons and ethylene contains 2 π-electrons. The sum of p and q is 6 and they are all suprafacial. Hence, this [4+2] cycloaddition is thermally allowed .

• overlap integral

$S=\int \psi {\psi }^{*}d\tau$ Equation 8. Calculation of overlap integral

The overlap integral is calculated by equation 8 and it is telling how well two orbitals are overlapped. The value of overlap integral is between 0 and 1. 0 means that the two orbitals do not have any overlap and 1 means that they perfectly overlap with each other. Table 3 is used to determine whether the wavefunction is symmetric or antisymmetric.

Table 3. Symmetric and Antisymetric wavefunction

Symmetric	Antisymmetric
ψ(r1,r2)=+ ψ(r2,r1)	ψ(r1,r2)=- ψ(r2,r1)

For two wavefunctions, the overlap integral will be 0 if the product of two wavefunctions is antisymmetric. If the product of two wavefunctions is symmetric, the overlap integral will be 1. Only when both of the wavefunctions are antisymmetric or both are antisymmetric, the overlap integral will be 1. As shown in MO diagram, the antisymmetric orbital will overlap with the antisymmetric orbital.

(Fv611 (talk) Your MO diagram is very nice, but there is some confusion in the discussion of symmetry and orbital overlap. The orbital overlap will only be 1 in case the two functions are exactly the same.)

Analysis of bond lengths

Table 4. IRC bond distance analysis

Fig.7 Disatance VS reaction coordination

Fig.8 Labelled molecule

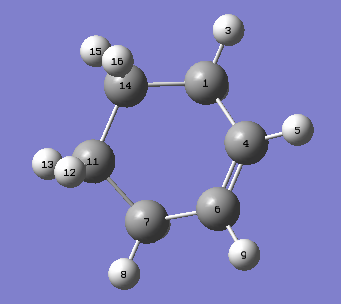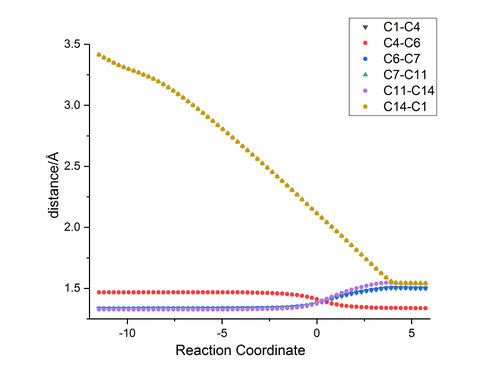
In Fig.7, it shows that the distances between C atoms change with reaction coordination. and Fig.8 shows the labelled molecule. Initially, the distance between C₁₄ and C₁ and distance between C₇ and C₁₁ are around 3.4 Å, which indicates there does not have any bond between those two atoms. The Van der Waal radius of C atom is 1.77Å 3.4 Å is smaller than twice of Van der Waals radius of C; therefore, C₁₄ is interacting with C₁ and a bond will be formed between them.

(Fv611 (talk) You should have focused your discussion on the length of the bonds at the transition state specifically.)

Table 4. Bond length of C-C bond

	C(sp3)-C(sp3)	C(sp3)-C(sp2)	C(sp2)-C(sp2)
Bond length/Å	1.542	1.488	1.459

Table 4. shows the literature value of C-C bond length with different hybridisation and comparing those with the Fig 7. It suggests C₁, C₇,C₁₁ and C₁₄ change from sp² to sp³; C₄ and C₆ remain sp². Besides that, this table also confirms the product is hexene. The distance between C₄ and C₆ is 1.338 Å, which is similar to the bond lenght of C(sp²)-C(sp²). The rest of bond lengths are around 1.5 Å; so the rest of bonds are C(sp³)-C(sp³).

Vibration

Transition State vibration	Inrinsic Reaction Coordinate(IRC)
Fig 9. Vibration Frequencies of Transition State	Fig 10. summary of IRC plot

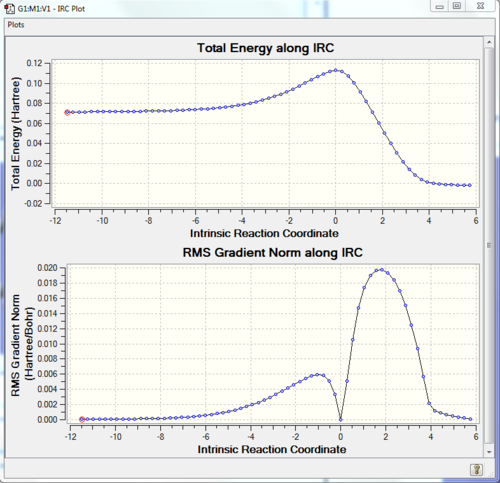As shown in Fig.9, there is only one imaginary frequency (at -948.8 cm^-1); so it justifies the transition state is right. However, it is not enough for determining the transition state. It is critical to do the IRC calculation. RMS Gradient should be zero in reactants, products and also transition state because they are local minima. However, for transition state, it is saddle point; hence, the second derivative should be negative.

According to the gif shown above, it shows that bonds are formed synchronously.

LOG File

Transition state:File:MG5715 TS E1 TS MO.LOG

Butadiene:File:MG5715 TS E1 BUTADIENE MO.LOG

Ethylene:File:MG5715 TS E1 ETHLYENE MO.LOG

Excercise 2: Reaction of Cyclohexadiene and 1,3-Dioxole

Fig.11 The reaction scheme of Cyclohexadiene and 1,3-Dioxole

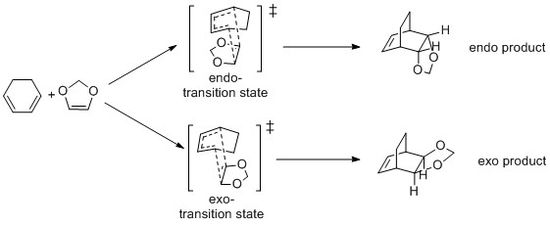
The reaction of cyclohexadiene and 1,3-Dioxole is also a Diels-Alder reaction, but this reaction will give two products (endo and exo) because of two possible transition states. The reaction scheme is shown in Fig.11 In this exercise, the transition state is opitimised by PM6

firstly and then optimised again by B3LYP

. Moreover, the transition state is determined by method 3

in this exercise.

MO analysis of exercise 2

(Fv611 (talk) This is not the way to draw two separate MO diagrams.)

Fig.12 MO diagram of Cyclohexadiene and 1,3-Dioxole

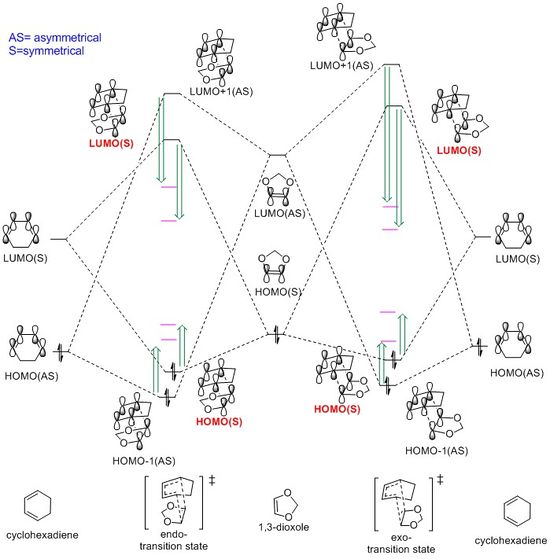
The MO diagram of this reaction is displayed in Fig.12The energies of product's MO is shown in black lines and the pink

lines represent the energies of transition states' MO, and all of them are drawn based on the relative energies calculated by B3LYP. Furthermore, the HOMO and LUMO of reactants are shown in Table 5. and the MOs of transition states are displayed in Table 6. 

Table 5. LUMO and HOMO of reactants

	HOMO	LUMO
Clycohexadiene
1,3-dioxole

Table 6. MO of Transition states

	ENDO TS	EXO TS
LUMO+1
LUMO
HOMO
HOMO-1

Secondary Orbital Interactions

Table 7. HOMO of Endo-TS and Exo- TS

	Endo-TS	Exo-TS
Jmol of computed HOMO
LCAO diagram of HOMO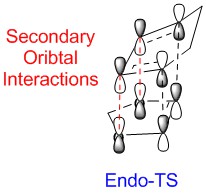

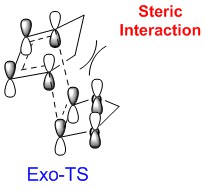The computed HOMO and LACO diagram of HOMO are shown in Table 7. Endo-product is more stable than Exo-product due to lack of steric clash with the methyl group in cyclohexadiene. Furthermore, the Endo-TS is lower in energy because of Secondary Orbital Interaction. The lone pair of oxygen could donate the electron density to the LUMO of cyclohexadiene; hence, the Endo-TS will be stabilised. Both the Endo-TS and Endo-product are lower in energy; so this reaction is endo-selective.

Inverse VS Normal Demand Diels-Alder Reaction

Fig.13 two tyes of Diels-Alder reaction

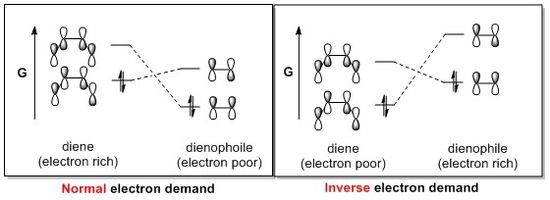
For a Diels-Alder reaction, the reactivity is controlled by relative energies of Frontier Molecular Orbitals (FMOs). There are two different types as shown in Fig.13:(1) Normal demand and (2) Inverse demand. Usually, the reaction of an all carbon diene with a hetero-dienophile will give a normal electron demand because the heteroatom in dienophile may withdraw the electron density from dienophile and lower the energy of MOs. The best way to justify whether the reaction is normal demand or inverse demand is to sequence the energy of reactants as shown in Table 8. If the HOMO of dienophile is lower than that of diene, it is normal demand, vice versa. The HOMO of cyclohexadiene is the lowest; hence, this reaction is inverse demand

Diels-Alder reaction. The reason is that the two oxygen atom in 1,3-dioxole donate the electron density toward the π-bonding and raise the energy of MOs.

Nf710 (talk) 19:39, 28 March 2018 (BST) Well done. this is shown really clearly with the diagrams and you even had he energy on the jmols.

Table 8. Single point energy of reactants

Endo-reaction	Exo-reaction

Activation Barrier and Energy changed

Table 9. Energies of reactants, products and transition states

	Energy calculated by PM6/kJmol-1	Energy calculated by B3LYP/kJmol-1
Cylcohexadiene	306.9	-612593
1,3-dioxole	-137.3	-701189
Endo-product	99.2	-1313849
Endo-TS	362.2	-1313622
Exo-product	99.7	-1313845
Exo-TS	364.7	-1313614

According to the energies of reactants, products and transition states (shown in Table 9), the reaction energy and activation energy could be calculated by the following equation:

Activation Energy = Transition state energy - Sum of energies of reactants
Reaction Energy = product energy - Sum of energies of reactants

Table 10. Reaction energy and activation energy for both Endo and Exo product.

	Activation Energy/kJmol-1		Reaction Energy/kJmol-1
	PM6	B3LYP	PM6	B3LYP
Endo-reaction	+192.6	+159.8	-70.3	-67.4
Exo-reaction	+195.1	+169.7	-69.9	-63.8

All the energy calculated is shown in Table 10. Both the activation energy and reaction energy for Endo-product are lower than those for Exo-product. A thermodynamically favourable product is more stable, which means it has more negative reaction energy. The kinetically favourable product has lower reaction barrier (activation energy). Hence, the endo-product of this exercise is both thermodynamically and kinetically favourable.

Nf710 (talk) 19:39, 28 March 2018 (BST) This is a really good section everything is clear and you have got the correct energies. Your diagram on sterics could have been slightly clearer. But well done.

LOG File

1,3-Dioxole:File:MG5715 TS E2 REACTANTS 2.LOG

Cyclohexadiene:File:MG5715 TS E2 REACTANTS 1.LOG

Exo-Transition State:File:MG5715 TS E2 EXO.LOG

Endo-Transition State:File:MG5715 TS E2 ENDO.LOG

Excercise 3 Diels-Alder vs Cheletropic

Fig.14 Reaction Scheme of o-Xylylene with SO₂

The reaction of o-xylylene with SO₂ could be either Diels-Alder or cheletropic reaction. For Diels-Alder reaction, o-Xylylene acts as diene and SO₂ acts as dienophile to form a six-membered ring and there are two possible products (endo-product and exo-product). As discussed in exercise 2, the Diels-Alder is endo-selective. For the cheletropic reaction, a five-membered ring will be formed and two new bonds are formed with the same atom. The reaction scheme of those reactions is displayed in Fig.14. In this exercise, the reactants, products and transition states were optimised by PM6

and B3LYP
and Method 3
was used to find the transition state. The reaction energy and activation energy were calculated to find out the favourable reaction.

(Endo is only kinetically preferred out of the DA reactions Tam10 (talk) 14:29, 16 March 2018 (UTC))

IRC Analysis

Table.11 The IRC of three possible reactions

	IRC
Cheletropic reaction
Endo Diels-Alder reaction
Exo Diels-Alder reaction

There are two different mechanisms for Diels-Alder reaction:(1)synchronous and symmetrical (concerted) mechanism and (2) multistage (non-concerted) and asynchronous mechanism.

• synchronous and symmetrical (concerted) mechanism

A very typical example of this mechanism is Exercise 1. The two new bonds are formed simultaneously and the two new bonds have the same bond length in the transition state.

• multistage (non-concerted) and asynchronous mechanism

The two bonds could not be formed at the same time because the bond length of them are different at transition state. Therefore, usually, a di-radical will be formed.

For Diels-Alder reaction, the distance between O and C in o-Xylylene is different from the distance between S and C in o-Xylylene at transition state because of distinct Van der Waal radii. Therefore, the bond does not form synchronously, which could be observed in the IRC in Table 11. However, for cheletropic reaction, the two now bonds are both formed between S atom and C in o-Xylylene; so the two bond are formed synchronously as shown in IRC.

(Be careful: it looks like you're saying the DA reactions are multistage, which involves an intermediate (all positive eigenvalues in Hessian/positive frequencies) Tam10 (talk) 14:29, 16 March 2018 (UTC))

Activation Energy and Reaction Energy

Fig.15 Energy diagram of o-Xylylene with SO₂

Table 12. Energies of reactants, products and transition states

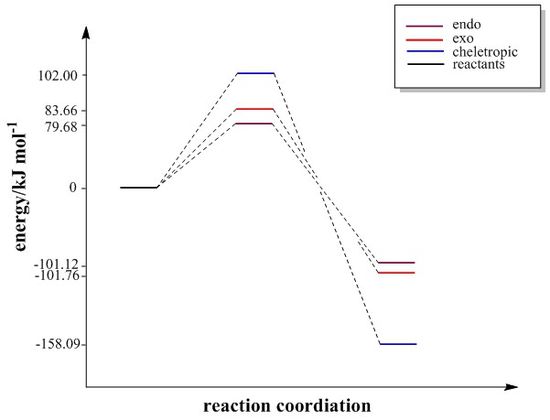
	Energy calculated by PM6/kJmol-1	Energy calculated by B3LYP/kJmol-1
O-Xylylene	469.5	-812604
SO2	-311.4	-1440362
Endo-product	57.0	-2253040
Endo-TS	237.8	-2252919.7
Exo-product	56.3	-2253041
Exo-TS	241.7	-2252919.8
Cheletropic product	-0.005251	-2253024
Cheletropic TS	260.1	-2252902

Table 13. Reaction energy and activation energy for both Endo and Exo product.

	Activation Energy/kJmol-1		Reaction Energy/kJmol-1
	PM6	B3LYP	PM6	B3LYP
Endo-reaction	+79.7	+46.2	-101.1	-73.9
Exo-reaction	+83.7	+46.1	-101.8	-73.2
Cheletropic	+102.0	+63.0	-158.1	-58.8

The energies of reactants, products and transition states are shown in Table 12 and the calculated reaction energy and activation energy are displayed in Table 13. The energy diagram (Fig.15) is drawn according to the energy calculated by PM6. The product of the cheletropic reaction is the most stable because of aromaticity. However, the activation energy of cheletropic product is quite high. Therefore, at low temperature, a sultine (kinetic product) will be formed but this reaction is reversible. At high temperature, a sulfolene will be formed and this reaction is irreversible.

(Well done doing the B3LYP calculations, but it must have taken a long time. The results are distinctly different to the PM6 calculations, so you could have commented on that Tam10 (talk) 14:29, 16 March 2018 (UTC))

Extension

Fig.16 Reaction Scheme of o-Xylylene with SO₂

There are two dienes in o-Xylylene and therefore, it has another possible Diels-Alder reaction as shown in Fig.16. The energy calculated is displayed in Table 14 and they are calculated by PM6.

Table 14. Energy of reactants, products, and transition states

	Energy calculated by PM6/kJmol-1
O-Xylylene	469.5
SO2	-311.4
Endo-product	172.3
Endo-TS	268.0
Exo-product	176.7
Exo-TS	275.8

Table 15. Reaction energy and activation energy for both Endo and Exo product.

	Activation Energy/kJmol-1	Reaction Energy/kJmol-1
Endo-reaction	+109.9	+14.2
Exo-reaction	+117.7	+18.6

Compare the energy in Table.15 with the data in Table.13, this reaction is quite unlikely to happen because the activation barrier is higher and the reaction energy is endothermic.

LOG File

o-Xylylene:File:MG5715 REACTANT PM6.LOG

SO₂:File:MG5715 SO2 PM6.LOG

Exo-Transition state:File:MG5715 EXO TS PM6.LOG

Endo-Transition state:File:MG5715 ENDO TS PM6.LOG

Cheletropic Transition state:File:MG5715 CHE TS PM6.LOG

Conclusion

In conclusion, Gauss View is a quite efficient way to locate the transition state and to calculate the energy of a reaction. Hence, it could suggest which product is thermodynamically favourable and which one is kinetically favourable. Besides that, it could mimic the reaction pathway by IRC, which can tell us whether the bonds are formed synchronously or not. One of the best way to confirm the transition state is to check the vibration frequency of transition state. For a transition state, it will always have only one imaginary frequency. According to this experiment, it suggests Diels-Alder reaction is endo-selective because of secondary orbital interaction and if the two bonds are formed with same atoms, they will form synchronously.