Rep:Mod:melody

Conformational analysis using Molecular Mechanics

The Hydrogenation of Cyclopentadiene Dimer

Cyclopentadiene Dimers

Cyclopentadiene dimerises to produce specifically the endo dimer rather than the exo dimer. Using Avogadro, the two products were defined and their geometries optimised using the MMFF94(s) force field option.

Cyclopentadiene Dimer Comparison
Diastereoisomer
Energy	kcal mol-1
Stretching	3.29872	3.38094
Angle Bending	31.42064	29.06625
Stretch Bending	-1.93752	-1.89925
Out-of-plane Bending	0.02382	0.01615
Torsion	-1.46181	-1.12786
Van der Waals	12.20843	12.63198
Electrostatic	14.05004	12.90736
Total Energy	57.60233	54.97559

Reaction mechanism for dimerisation of cyclopentadiene

Although the endo product is higher in energy than the exo product by 2.63 kcal/mol, the less thermodynamically stable endo product is formed as there is stabilizing secondary orbital interaction (of the pi orbitals) in the transition state of the endo product, whereas there is no such interaction in the transition state of the exo product. The dimerisation of cyclopentadiene is thus kinetically controlled, and the endo product the kinetic product.

The energy difference between endo and exo products is largely due to the increase in the angle bending energy, with a difference of 2.35 kcal mol^-1. The angle bending energy is defined as the energy involved to bend a bond away from its equilibrium angle. In the endo conformation, the ring, which is formed by joining two adjacent axial position (concave arrangement for the two rings), tends to bend upwards to the equatorial position to minimize steric hindrance with the other ring and hence causes an increase in angle bending energy. In the exo product, the ring is joined at the equatorial position (linear arrangement for the two rings) and avoids steric hindrance with the other ring, hence there is less increase in angle bending energy.

Hydrogenation

Hydrogenation of the endo dimer proceeds to give initially one of the dihydro derivatives 3 or 4. Only after prolonged hydrogenation is the tetrahydro derivative formed.

Cyclopentadiene Dimer Comparison
Diastereoisomer
Energy	kcal mol-1
Stretching	3.31116	2.82326
Angle Bending	31.93515	24.68525
Stretch Bending	-2.10212	-1.65728
Out-of-plane Bending	0.01317	0.00027
Torsion	-1.46918	-0.37919
Van der Waals	13.63801	10.63816
Electrostatic	5.11952	5.14701
Total Energy	50.44571	41.25748

Hydrogenation of cyclopentadiene endo dimer

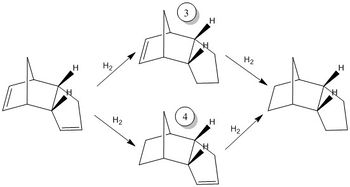
Product 4 is lower in energy than product 3 by 9.19 kcal mol^-1. The difference in energy is again largely due to the angle bending energy difference of 7.25 kcal mol^-1, and to a smaller extent, the Van Der Waals energy difference of 3.00 kcal mol^-1 due to the greater steric repulsion in 3. The large difference in the angle bending energy is due to the geometry of the 4 sp² carbons in the endo product of the dimer. sp² carbons in a ring equal or smaller than 6-membered ring is generally unstable as the 120° angle favoured by sp² centres cannot be geometrically achieved without ring strain. The double bond at the norbornene part of the molecule has sp² carbons shared by both a 5-membered and a 6-membered ring whereas the sp2 carbons at the other end only causes ring strain to one 5-membered ring. Hence, product 4 would have more bond angles that are closer to equilibrium and hence, possesses lower ring strain and a lower angle bending energy. Product 4 should be formed as the thermodynamic product, as confirmed in literature. The hydrogenation of endo dicyclopentadiene is thus thermodynamically controlled, and the the first hydrogenation occurs at the norbornene part of the molecule.

Atropisomerism in an Intermediate related to the Synthesis of Taxol

In the total synthesis of Taxol (an important drug in the treatment of ovarian cancers), a key intermediate 9 or 10is initially synthesised with the carbonyl group pointing either up or down. By using the MMFF94(s) force field option in Avagadro, the relative stabilities of these two atropisomers were explored. After experimenting with the different conformations of intermediate 9 and 10, it was found that a "chair" conformation of both compounds 9 and 10, as shown in the table below, resulted in optimised structures with the lowest energies. The energies of the chair conformations of intermediates 9 and 10 are compared below.

Cyclopentadiene Dimer Comparison
Diastereoisomer
Energy	kcal mol-1
Stretching	7.65248	7.56126
Angle Bending	28.27472	18.82557
Stretch Bending	-0.07951	-0.13605
Out-of-plane Bending	0.97217	0.83644
Torsion	0.31893	0.19401
Van der Waals	33.10145	33.32591
Electrostatic	0.30721	-0.05433
Total Energy	70.54748	60.55280

Atropisomer 10 is lower in energy, with a difference of 9.99 kcal/mol, and therefore is more thermodynamically stable than atopisomer 9. The difference in energy is largely due to the angle bending energy (9.45 kcal/mol) which makes up the majority of the total energy difference. This indicates that the bond angle of the carbonyl group in atropisomer 10 is much closer to the equilibrium angle than atopisomer 9.

This can be proven by inquiring the bond angles of the bonds involving sp² and sp³ hybridised carbon atoms in the carbonyl group in Atropisomer 9 and 10 in Gaussview, which is summarised below.

Atropisomer	Bond Type	Carbonyl Group Bond Angles (°)	Equilibrium Angle (°)
	Bonds involing sp2 hybridised carbons	117-123	120
	Bonds involing sp3 hybridised carbons	100-108	109.5
	Bonds involing sp2 hybridised carbons	120-121	120
	Bonds involing sp3 hybridised carbons	105-109	109.5

Maier and Schleyer concluded that double bond joined to a bridge is particularly stable due to its cage structure, thus, its corresponding hydrogenated product will experience more strain, which explains why bridgehead alkenes react slowly.

Other conformers for these atropisomers include a boat structure, which is less stable than the corresponding chair conformation. The increase in energy is due to an increase in angle bending torsional energy as the cyclohexane ring experiences greater torsional strain in the eclipsed boat conformation.

Spectroscopic Simulation using Quantum Mechanics

Optimization of Molecule 18

Molecule 18

Molecule 18 Optimization
	Energy	kcal mol-1
	Stretching	14.99958
	Angle Bending	30.80948
	Stretch Bending	-0.07951
	Out-of-plane Bending	0.62729
	Torsion	0.89658
	Van der Waals	49.39433
	Electrostatic	-6.05522
	Total Energy	100.44220

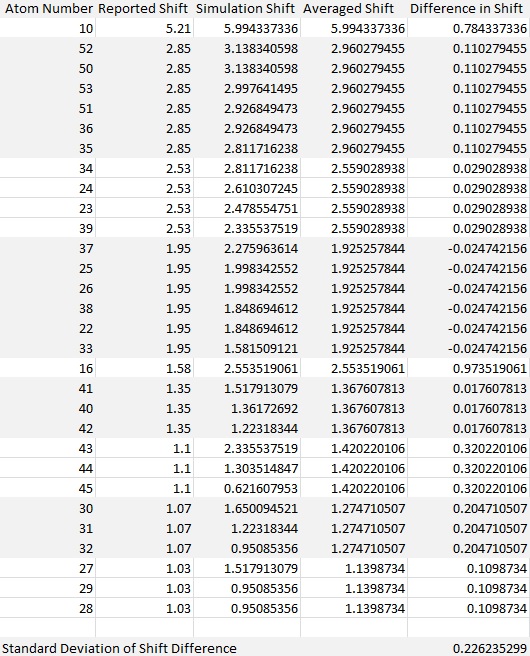
The molecule 18 is a derivative of molecule 10, for which spectroscopic information has been reported. The objective here is to simulate the ¹H and ¹³C spectra and compare them with the literature values to see if the latter has been correctly interpreted and assigned.

Using the Avogadro or ChemBio3D program, and using the MMFF94s mechanics force field, the starting molecules 18 was optimized to an energy minimum. Based on the previous calculations involving the cyclopentadiene dimer and the Taxol intermediate atropisomer, it was predicted that the lowest energy conformation of compound 18 would be an endo (at the large ring), chair (at the smaller cyclohexane ring) conformer, as illustrated in the jmol file on the left. This structure is also supported by crystallographic data from literature.

Spectroscopic Simulation of Molecule 18

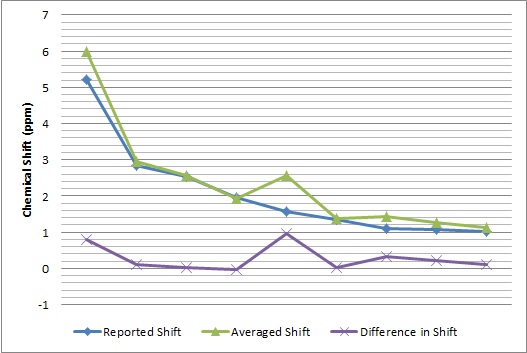
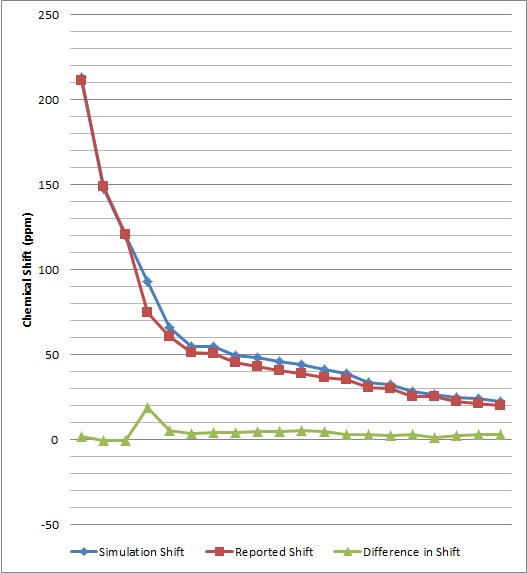
By using Avogadro's Gaussian Geometry optimization and illustrating using GaussView, the following NMR data was obtained. The .log file of the simulation can be found here, and the digital repository here DOI:10042/28194 .

Atom Numbering
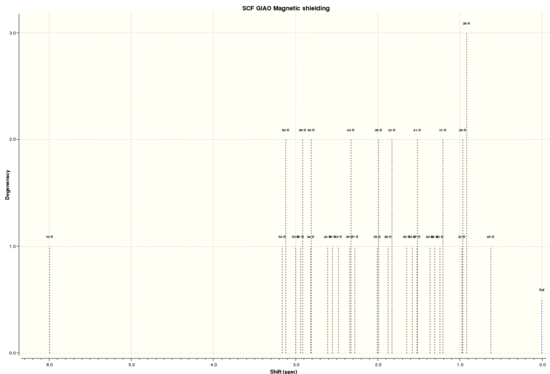
1H NMR		Shift (ppm) Degeneracy Atoms 5.9943373355 1.0000 10 3.1383405979 2.0000 52,50 2.9976414945 1.0000 53 2.9268494729 2.0000 51,36 2.8117162381 2.0000 34,35 2.6103072452 1.0000 24 2.5535190605 1.0000 16 2.4785547510 1.0000 23 2.3355375185 2.0000 39,43 2.2759636135 1.0000 37 1.9983425520 2.0000 25,26 1.8486946118 2.0000 38,22 1.6500945214 1.0000 30 1.5815091205 1.0000 33 1.5179130786 2.0000 27,41 1.3617269195 1.0000 40 1.3035148468 1.0000 44 1.2231834398 2.0000 42,31 0.9508535600 3.0000 32,29,28 0.6216079526 1.0000 45
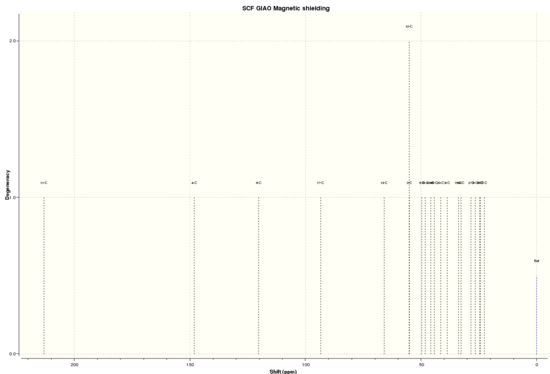
13C NMR		Shift (ppm) Degeneracy Atoms 213.0961325830 1.0000 11 148.0547320284 1.0000 4 120.2667148682 1.0000 9 93.3213936895 1.0000 17 65.9859553102 1.0000 13 55.0715405775 2.0000 3,12 49.7214718290 1.0000 5 48.1628662916 1.0000 18 45.8501042512 1.0000 49 44.1990174424 1.0000 48 41.3930608867 1.0000 20 38.7739494869 1.0000 8 33.7645805938 1.0000 15 32.6242885826 1.0000 14 28.4566038455 1.0000 2 26.5581305940 1.0000 6 24.6172011030 1.0000 1 24.2187982580 1.0000 19 22.6332903141 1.0000 7

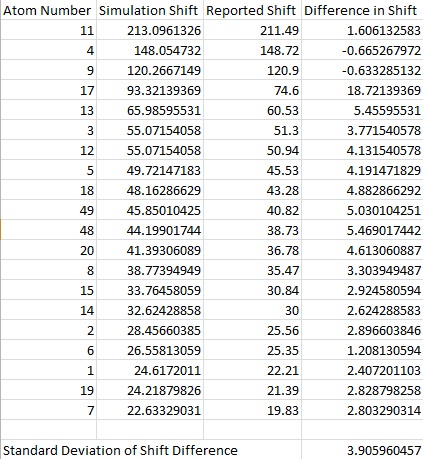
The obtained spectroscopic data was then compared with literature values shown below.

Literature Values
1H NMR Comparison	13C NMR Comparison

Analysis of the Properties of Synthesised Alkene Epoxides

Structure of Catalsysts

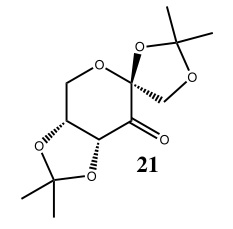
Structure 21

Based on the Cambridge crystal database (CCDC) using the Conquest program, molecule 21 was visualized on the Mercury program.

It was found that the six membered heteroatomic ring of structure 21 adopted a chair conformation, which was expected, to minimize torsional strain, with the Oxygen atom (O² - with superscript ² indicating that the atom is numbered 2) as the non-planar end. It was also discovered that substituent oxygen atoms such as O² were in an axial position rather than the more sterically unhindered equatorial position. This allows an anti-periplanar alignment between the oxygen lone pair, which is a good donor, and the adjacent C-O² σ* orbital which is a good acceptor, leading to a stabilising interaction. Consequently, O⁶ will lose electron density and the C-O² bond lengthened as electrons are interacting with its anti-bonding orbital. The anomeric effectalso occurs in five-membered rings, but to a lesser extent due to deviations from an anti-periplanar alignment.

There are three anomeric centres present in the molecule 21, which are at C², C⁹ and C¹⁰. At C², the C²-O² (1.423Å) bond is longer than at C²-O⁶ (1.415Å). At C⁹ and C¹⁰, C⁹-O²(1.454Å) and C¹⁰-O⁴ (1.456Å) are both longer than adjacent C⁹-O¹(1.423Å) and C¹⁰-O⁵ (1.428Å) bonds. Interestingly, even though O¹ and O² appear symmetrical around C⁹, and similiarly for O⁴ and O⁵ around C¹⁰, only one oxygen's lone pair (O¹ for C⁹, O⁵ for C¹⁰) can align in an anti-periplanar fashion to the σ* orbital of the adjacent C-O bonds. Otherwise, the mutual anomeric effects would cause each adjacent C-O bonds to be equaivalent in length.

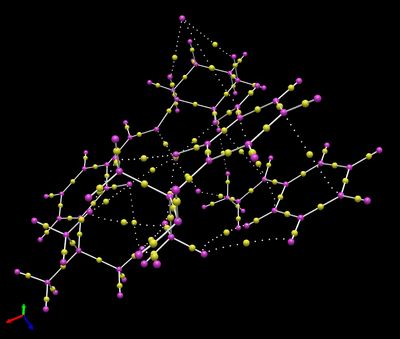
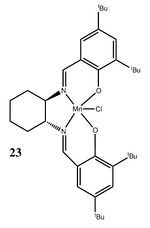
Structure 23

Based on the Cambridge crystal database (CCDC) using the Conquest program, molecule 23 was visualized on the Mercury program.

Molecule 23 has a 5-coordinated manganese centre with a square pyramidal structure where 4 atoms joined by ring-like structures and bridges are coordinated to the metal center in an approximate plane, with a perpendicular chlorine atom coordinated to the metal center. This approximate planar nature is due to the delocalisation of electron densities at the salen ligands at either sides. The cyclohexane ring adopts a low energy chair conformation and has two chiral C atoms attached to N, thus defining the stereochemistry of the Jacobsen catalyst to be either (R,R) or (S,S).

The bulky ^tBu groups on the Salen ligands prevent a side-on approach of the alkenes due to steric hindrance, ensuring epoxidation enantioselectivity. Without the ^tBu groups, alkenes could have side-on approach to the catalyst, as shown when the ^tBu groups were replaced with methyl gourps. . As seen above, the two central ^tBu groups are in close proximity, and the interaction between the hydrogen atoms (represented by the green lines) is an attractive interaction. The maximum attraction for non-bonded hydrogens are at 2.4Å, while repulsion only occurs when the atoms are less than 2.1Å apart from each other. This attractive interaction, coupled with the steric effects of the outer ^tBu groups, results in increased catalyst thermodynamic stability and selectivity.

Simulated NMR properties of Epoxides

Styrene Oxide

Enantiomer	R-Styrene oxide	S-Styrene oxide
Labelled Structures
3D Structures
Digital Repository	DOI:10042/28208 & .log File	DOI:10042/28208 & .log File
Simulated 1H NMR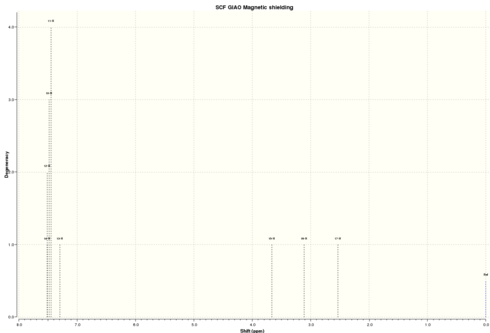
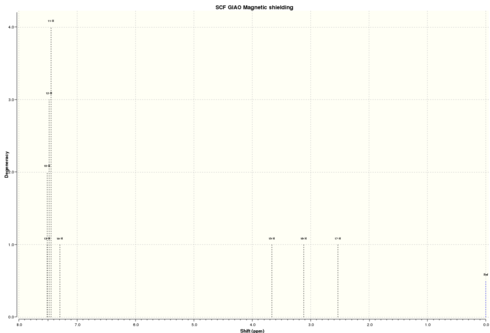
Simulated 13C NMR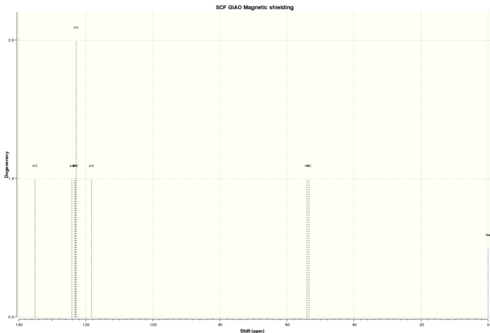

Dihydronaphthalene Oxide

Enantiomer	(S,R)-dihydronaphthalene oxide	(R,S)-dihydronaphthalene oxide
Labelled Structures
3D Structures
Digital Repository	DOI:10042/28211 & .log File	DOI:10042/28210 & .log File
Simulated 1H NMR
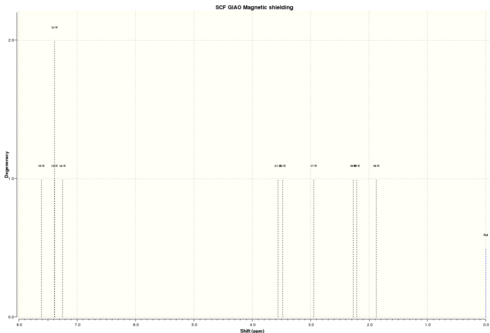
Simulated 13C NMR

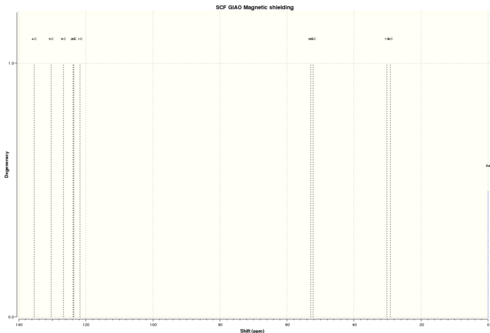
Assigning the absolute configuration of the product

Simulated chiroptical properties

Computational methods can be used to calculate the expected chiroptical properties of epoxides for a specified enantiomer, which can be comparing with experimental and literature values to predict the enantioselectivity of the catalyst. Three chiroptical properties can be useful in this regard:

The optical rotation at a specified wavelength of light (the optical rotatory power, or ORP) or the values for a range of wavelengths (the Optical rotatory dispersion, or ORD). The electronic circular dichroism (ECD) The vibrational circular dichroism (VCD).

All these properties can be computed nowadays. However, only the first (the optical rotation) can be readily measured in the Imperial College 3rd year laboratory. The ECD, which in effect is the UV/Vis spectrum recorded with polarised light, is actually useless for the epoxides because no appropriate chromophore exists for the epoxides. VCD is an excellent technique, but the appropriate instrument is not available in the department. Thus, due to these limitations, only the optical rotation was simulated, with the following results.

Epoxide	R-Styrene oxide	S-Styrene oxide	(S,R)-dinaphthalene oxide	(R,S)-dinaphthalene oxide
Simulated Optical Rotation (CHCl3, 589nm, 25°C)	-30.14°	+30.41°	+155.81°	-155.82°
Literature Optical Rotation ((CHCl3, 589nm)	-23.7°, 31°C	+32.1°, 25°C	+133°	-144.9°, 25°C
Digital Repository	DOI:10042/28214	DOI:10042/28244	DOI:10042/28243	DOI:10042/28242

It was observed that literature values are lower than the simulated values in magnitude. This is most likely due to a less than 100% enantiomeric purity. The simulation does not take this into consideration, thus, during simulation, a 100% enantiomeric purity was assumed. Temperature could also have been a factor in the difference in optical rotation, but this effect of this difference is difficult to predict. However, the simulated and literature values seem to to be satisfactorily in agreement.

Calculated properties of transition state for the reaction

The relative computed free energy of the transition state can be used as a check for the enantiomeric assignment obtained by comparing computed and calculated optical rotations of the epoxide. This is calculated via the Curtin-Hammett Principle, which relates the relative concentration of two products to the difference in energy of the transition states for two different conformers of a molecule.

The principle can be simplified to the following equations;

K=e^{-(ΔG°_TS/RT)}, where K=[A]/[B], the ratio of concentration between two conformers, and [A] and [B] are the concentrations of conformer A and B respectively, and ΔG°_TS is the relative computed free energy of the transition state, i.e, the difference between the energy levels of the transition states for each enantiomer.

The Enantiomeric Excess (EE) is defined as ([A]-[B])/([A]+[B]) * 100%.

Since K=[A]/[B], [A]=K[B], and thus, EE= (K[B]-[B])/K[B]+[B]) * 100%.

Therefore, EE = (K-1)/(K+1) * 100%

A list of possible transition states for trans-β methyl styrene using the Shi and Jacobsen's catalyst is available in digital repositories. By calculating the energy difference between the lowest energy transition state (which represents the most probably pathway for each catalytic epoxidation), ΔG°_TS/RT can be calculated.

Calculated Enantiomeric excess of Trans-β methyl styrene using Shi Catalyst

Free Energy of lowest (R,R)-Trans-β-methyl Styrene Oxide TS (1) -1343.032443 Ha Free Energy of lowest (S,S)-Trans-β-methyl Styrene Oxide TS (2) -1343.024742 Ha ΔGTS (1)-(2)=(3) -0.007701 Ha ΔGTS (1)-(2)=(3) -2.021897257 x 104 J/mol K 3499.272792 Enantiomeric Excess 99.9%

Lowest Energy (R,R)-Trans-β-methyl Styrene Oxide TS

While, the calculation has overestimated the enantiomeric excess of the (R,R)-Trans-β-methyl Styrene Oxide enantiomer (99.9%), when compared to literature values of 93.2% , it is in general agreement that the R,R enantiomer is largely the major product. The lowest energy transition state corresponds to the endo alignment of the methyl styrene's phenyl ring with the fructose component of the Shi catalyst. The endo alignment results in a stabilising secondary orbital interaction.

Ceteris paribus, the epoxidation should be even more enantiomerically selective than calculated, as the second lowest transition state energy (-1343.029272 Ha) would also leads to the (R,R) product. However, the literature value is lower than even the first calculated value. One possible reason for this could be due to the simulation being performed with an assumed water solvent, although the actual reaction was performed in an organic and aqueous salt mixture. Solvent effects in terms of polarity and hydrogen bond formating ability will affect transition state energies, causing deviations between the theoratical and the actual values. The other possible reason for the unexpectantly smaller enantiomeric ratio could be due to partial epoxidation of the alkene mvia a non-catalytic pathway, which could lead a less enantiomerically selective reaction pathway.

Calculated Enantiomeric excess of Trans-β methyl styrene using Jacobsen Catalyst

Free Energy of lowest (S,S)-Trans-β-methyl Styrene Oxide TS (1) -3383.262481 Ha Free Energy of lowest (R,R)-Trans-β-methyl Styrene Oxide TS (2) -3383.254344 Ha ΔGTS (1)-(2)=(3) -0.008137 Ha ΔGTS (1)-(2)=(3) -2.13637x 104 J/mol K 5554.228363 Enantiomeric Excess 99.9%

Lowest Energy (S,S)-Trans-β-methyl Styrene Oxide TS

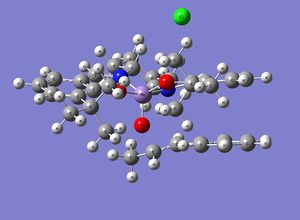In the Jacobsen styrene transition state complex however, the (S,S)-Trans-β-methyl Styrene Oxide Transition state is the lowest energetical transition state. The difference between the transition state energy is due to the fact that in the endo conformation, there is stabilising non-covalent pi stacking between the phenyl ring of methyl styrene and the salen ligand of the catalyst whereas this interaction is absent in the exo alignment. This is due to how the alkene of the substrate must orientate in correct position for oxygen transfer at the Manganese centre and thus affects the alignment of its phenyl group with the catalyst.

The simulated Enantiomeric Excess value of 99.9% of (S,S) over (R,R) is agreeable with literature sources (91-92%) . Similiar to the enantiomeric ratio via Shi Catalyst, this reduced magnitude in enantiomeric selectivity coul be due to solvent effects and a non-catalytic reaction pathway.

Non-covalent Interactions in the Active-site of the Reaction Transition State

Orbital

Non-covalent interactions (NCI) include hydrogen bonds, electrostatic attractions and dispersion-like close approaches of pairs of atoms. As for normal covalent bonds, such NCI interactions can be defined by the properties of the electron density (and its curvatures. The NCI shown on the left was generated with the lowest energy transition state of a Jacobsen epoxidation on S,S-trans-β methyl styrene. The colours indicate whether the interaction is attractive (blue is very attractive, green mildly attractive, yellow mildly repulsive and red is strongly repulsive). It was observed that the alkene is aligned endo to the catalyst, allowing an attractive interaction between the phenyl group of the methyl styrene and the phenyl group of the Salen ligands, lowers the transition state energy and thus improving enantiomeric selectivity. Additionally, the two phenyl groups are also in a staggered conformation, thus minimizing steric strain. The attraction between the tBu groups also supports the hypothesis that the internuclear distance between the tBu H atoms promoted an attractive interaction.

Electronic Topology (QTAIM) in the Active-site of the Reaction Transition State

One limitation of NCI is that it does not show the exact atoms which are interacting, but instead, only shows the area of interaction. This is overcome with the use of QTAIM, which allows us to visualize the exact atoms which are interacting. The yellow dots in the QTAIM represents bond critical points (BCP). BCPs are where the first derivative of electron density with respect to distance is zero. By observing the QTAIM figure, it was found that there are 7 BCPs between the trans-β methyl styrene and the Jacobsen catalyst. (Between phenyl carbons, between the phenyl hydrogen and the tert-butyl hydrogen, between the benzylic carbon and N of the diimine and between the terminal hydrogen with the hydrogen of the cyclohexane ring). However, QTAIM is limited in that it is not able to tell whether the interactions are attractive or repulsive. This is instead complemented by NCI, which is able to tell whether the interactions are attractive interactions which stabilise the transition state, which is the case in this transition state. The relative distance of the BCP between atoms is observed to be different for the phenyl C-H bond. The BCP is further away from the more electronegative C atom, as the greater electron density results in a steeper electron density gradient and thus extends further along the bond before the gradient reaches zero.

Possible Alkenes for Further Investigation

A reaxys substructure search was undertaken to find an epoxide with a molecular weight under 200 g/mol and an optical rotation above -300 and below +300 degrees. 1-phenyl-7-oxa-bicyclo heptane was chosen as it is a small moelcule with a molecular weight of 174 g/mol and racemises when the equivalent alkene is epoxidised to form R,R and S,S enantiomers.

The R,R enantiomer has an optical rotation of 116 degrees, whereas the S,S enantiomer has an optical rotation of 92 degrees in benzene. The molecule is also available to buy from Sigma-Aldrich if ever the optical rotations should want to be examined experimentally. It would be interesting to see if the literature values for the optical rotations matched the experimental values well. References