Rep:Mod:mcy3cts
Transition States and Reactivity
Submitted by Michael W. H. Cheung (mwc14)
(Far too many JMols on this page. Took ~15 mins to load. If you want to use this many it's better to place them in different pages Tam10 (talk) 12:19, 9 November 2016 (UTC))
Introduction
In a 2D reaction profile, a maximum is where the first derivative of the reaction coordinate, which indicates the gradient, is zero; and the second derivative, which indicates the curvature, is negative. At the minimum, the gradient is zero while the curvature is positive. A potential energy surface is a function of the potential energy of the reaction against the relative positions of the atoms participating in the reaction. [1] In a chemical reaction, the transition state is defined as the maximum in a 2D reaction profile.[1] The reactants, the intermediates, and the products are at relative minima, which indicate the most stable structures of molecules in that particular reaction coordinate. This can be computed using a quantum chemical software, and relevant data can be extracted from the software to illustrate the transition state, the reaction coordinate, and subsequently to compare possible reaction pathways of chemical reactions.
Using Gaussian 09W, the reactants and the products can be optimized to minima by using a variety of methods, such as PM6 and DFT-B3LYP, which were mainly used in this lab. The transition state can also be optimized using similar methods. The intrinsic reaction coordinate can be computed using calculated force constants to illustrate how the reaction commences. Frequency calculations can be commenced to visualize vibrations and molecular orbitals in the molecule.
In this page, all calculations were done by Gaussian 09W. The reactants, the transition state, and the products were optimized, and the frequencies and the intrinsic reaction coordinates were computed.
Nf710 (talk) 20:42, 16 November 2016 (UTC) Good introduction
Exercise 1

The reaction between 1,3-butadiene and ethene is a pericyclic Diels-Alder reaction, involving interactions between π orbitals in both molecules. The reactants, the transition state, and the products were optimized at the PM6 level. Frequency and IRC calculations were commenced.
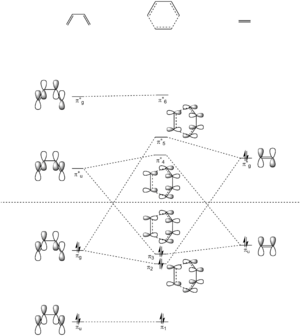
Molecular Orbital Analysis
The following diagram shows the proposed π molecular orbitals (MOs) for the formation of the transition state between butadiene and ethene.

Nf710 (talk) 20:44, 16 November 2016 (UTC)Really nice MO diagram
First, the reactants, butadiene and ethene, were optimized. The π MOs were illustrated in the following table.
| Molecule | Butadiene | Ethene | ||||
|---|---|---|---|---|---|---|
| LUMO | ||||||
| Corresponds to the π*u orbital | Corresponds to the π*g orbital | |||||
| HOMO | ||||||
| Corresponds to the πg orbital | Corresponds to the πu orbital |
The transition state was optimized, and the MOs corresponding to HOMO-1, HOMO, LUMO, and LUMO+1 were visualized.
| Transition State | |||
|---|---|---|---|
| LUMO+1 | |||
| Corresponds to π*5 orbital | |||
| LUMO | |||
| Corresponds to π*4 orbital | |||
| HOMO | |||
| Corresponds to π3 orbital | |||
| HOMO-1 | |||
| Corresponds to π2 orbital |
According to the MO diagram, and confirmed by the computed MOs, only the MOs with the same symmetry labels interact with each other. In this case, the butadiene π*u MO interacts with the ethene πu MO, and similarly, the butadiene πg MO interacts with the ethene π*g MO. Therefore, a reaction is allowed when the symmetry label of the MOs of the reactants are the same, and forbidden when the symmetry label of the MOs of the reactants are different.
Thus, the orbital overlap integral is zero in a gerade-ungerade interaction, and non-zero in gerade-gerade and ungerade-ungerade interactions.
Bond Length Analysis
Since the reaction involves a carbon-carbon bond formation, the C-C bond lengths of the reactants before the reaction, at transition state, and the C-C bond lengths of the products are studied. The carbon atoms are labeled in Diagram 2.
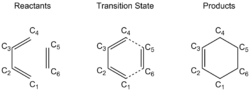
| State | C1 - C2 (Å) | C2 - C3 (Å) | C3 - C4 (Å) | C4 - C5 (Å) | C5 - C6 (Å) | C6 - C1 (Å) |
|---|---|---|---|---|---|---|
| Reactants | 1.335 | 1.468 | 1.335 | N/A | 1.327 | N/A |
| Transition State | 1.380 | 1.411 | 1.380 | 2.115 | 1.382 | 2.115 |
| Products | 1.501 | 1.338 | 1.501 | 1.540 | 1.541 | 1.540 |
As the reaction progresses, the bond lengths between C1 - C2, C3 - C4, and C5 - C6 increases, while that between C2 - C3 decreases. The increases in bond lengths suggest changes from a C-C double bond to a C-C single bond, while the decrease in bond length suggests a change from a C-C single bond to a C-C double bond. Typical bond lengths for a C-C single bond is 1.54 Å, while that of a C-C double bond is 1.33 Å.[2] Comparing these to the calculated bond lengths, it is evident that the bond order of the C-C bonds of the reactants change while forming the product. The newly formed C-C bonds are identified as C-C single bonds.
The Van der Waals radius of the carbon atom is 1.70 Å.[3] At the transition state, the lengths of C4 - C5 and C6 - C1 (2.115 Å) is shorter than 2 Van der Waals radii. This indicates that at the transition state, the C-C bond is indeed forming.
Nf710 (talk) 20:46, 16 November 2016 (UTC) Correct conclusion of the VdW
Vibration Analysis
| Reaction Path at Transition State | Lowest positive frequency |
From observing the reaction path, it is evident that the formation of the two bonds is synchronous, as both reaction centres converge simultaneously. The lowest positive frequency also illustrates this behaviour, however, suggests that the bonds form one at a time, where one of the ethene C atom moves towards the butadiene double bond, while the other one moves away. Thus, the lowest positive frequency suggests an asynchronous formation mechanism, while the reaction path suggests a synchronous one.
Nf710 (talk) 20:58, 16 November 2016 (UTC) This section was done well
Exercise 2

The reaction between cyclopentadiene and benzoquinone was studied. The reactants, transition state and the products were optimized with B3LYP/6-31G(d).
Molecular Orbital Analysis
As the reaction is a Diels-Alder reaction, the MO diagram constructed for butadiene and ethene can be applied to this reaction as well. The following discussion will reference MOs named in the MO diagram for a comparison between predicted MOs and computed MOs.
Illustrated below is the MOs that are correlated to the transition state MOs in the MO diagram.
| MO Number | Endo-TS | Exo-TS | ||||
|---|---|---|---|---|---|---|
| LUMO+1 | ||||||
| Corresponding to π*5 orbital | ||||||
| LUMO | ||||||
| Corresponding to π*4 orbital | ||||||
| HOMO | ||||||
| Corresponding to π3 orbital | ||||||
| HOMO-1 | ||||||
| Corresponding to π2 orbital | ||||||
Nf710 (talk) 21:02, 16 November 2016 (UTC) This is very easy to compare. nice formatting.
Reaction Energies and Reaction Barriers
The following table shows the computed energy values of the reactants.
| State | Gibbs Free Energy (Hartrees) | Gibbs Free Energy (kJ mol-1) |
|---|---|---|
| Cyclopentadiene | -194.034782 | -509438.320141 |
| Benzoquinone | -381.396831 | -1001357.3797905 |
| Reactants total | -575.431613 | -1510795.6999315 |
The comparison of the reaction energies and reaction barriers between the endo and the exo transition state is tabulated in the following table.
| State | Endo TS Gibbs Free Energy (kJ mol-1) |
Exo TS Gibbs Free Energy (kJ mol-1) |
|---|---|---|
| Reactants | -1510795.6999315 | -1510795.6999315 |
| Transition State | -1510670.3113025 | -1510663.6215285 |
| Product | -1510783.719775 | -1510782.7824715 |
| Reaction barrier | 125.388629 | 132.078403 |
| Reaction energy | 11.9749055 | 12.91746 |
From the table, the reaction barrier of the Endo TS is lower than that of the Exo TS. The Endo product is thus the kinetically favourable product. On the other hand, the reaction energy of the Exo TS is lower than that of the Endo TS. The Exo product is thus the thermodynamically favourable product. The Endo TS has a lower reaction barrier mainly because only there is a symmetrical interaction between the reaction centres, but also there is a secondary interaction between the non-bonding orbitals of the reactants. Thus this lead to the Endo product being the kinetically favourable one.
Nf710 (talk) 10:37, 21 November 2016 (UTC) Your results are correct, however you have calculated the energies from infinate seperation. In future you coud do it from the first and last point on the IRC as there is a significant seperation energy.
Exercise 3
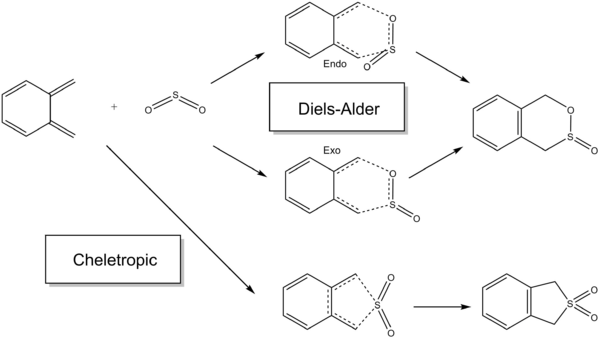
The reaction between xylylene and sulphur dioxide was studied. Below is the intrinsic reaction coordinate (IRC) of the Diels-Alder and Cheletropic reactions. Please click into the file to see the animation.
|

|

|
| IRC of Diels-Alder Reaction via Endo TS | IRC of Diels-Alder Reaction via Exo TS | IRC of Cheletropic Reaction |
As the reaction progresses, the bonds in the 6-membered ring in xylylene changes from distinctive single and double C-C bonds to delocalized C-C bonds.
Reaction Energies and Reaction Barriers
The following table shows the computed energy values of the reactants.
| State | Gibbs Free Energy (kJ mol-1) |
|---|---|
| Xylylene | 469.344882 |
| SO2 | -311.421057 |
| Reactants total | 157.923825 |
(Taking the sum of the reactants is effectively taking them at infinite distance without any interaction. You are therefore including the interaction energy into your calculations which won't represent the true barrier Tam10 (talk) 12:19, 9 November 2016 (UTC))
The comparison of the reaction energies and reaction barriers between the endo and the exo transition state, as well as that of the cheletropic reaction, is tabulated in the following table.
| State | Diels-Alder Endo TS Gibbs Free Energy (kJ mol-1) |
Diels-Alder Exo TS Gibbs Free Energy (kJ mol-1) |
Cheletropic Gibbs Free Energy (kJ mol-1) |
|---|---|---|---|
| Reactants | 157.923825 | 157.923825 | 157.923825 |
| Transition State | 237.7626545 | 241.7376615 | 260.087281 |
| Product | 56.983852 | 56.327477 | 0.0131275 |
| Reaction barrier | 79.8388295 | 83.8138365 | 102.163456 |
| Reaction energy | -100.939973 | -101.596348 | -157.9106975 |
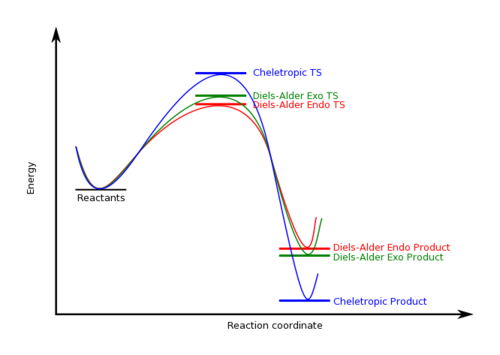
From the table, the Diels-Alder reaction via the Endo TS has the lowest reaction barrier, meaning that the Diels-Alder Endo-product is the kinetically favourable product. The cheletropic reaction has the lowest reaction energy, meaning that the cheletropic product is the thermodynamically favourable product.
Diagram 4 shows the reaction profile of the reactions.
Side Reaction
Xylylene has another diene located in the 6-membered ring. The reaction between this diene and SO2 was studied, and the following table shows the reaction barriers and the reaction energies of the reaction via the endo TS and the exo TS.
| State | Side Reaction Diels-Alder Endo TS Gibbs Free Energy (kJ mol-1) |
Side Reaction Diels-Alder Exo TS Gibbs Free Energy (kJ mol-1) |
|---|---|---|
| Reactants | 157.923825 | 157.923825 |
| Transition State | 275.8219025 | 267.984785 |
| Product | 176.706652 | 172.259055 |
| Reaction barrier | 117.8980775 | 110.06096 |
| Reaction energy | 18.782827 | 14.33523 |
As shown in the table, the reaction barrier and the reaction energy of both reactions greatly exceed that of the previously described in section 4.1. Both reaction are also endothermic. Therefore, this side reaction is both kinetically and thermodynamically unfavourable.
Conclusion
In this computational lab, various calculations were commenced in this lab, including calculations with Gaussian 09W, optimizing the reactants, transition state, and the products respectively. The intrinsic reaction coordinate and the frequency were also computed. These calculations give a great amount of information in determining symmetry restrictions, reaction barriers, reaction energy, and reaction profile.
The transition states of three pericyclic reactions were studied. Molecular orbital symmetry plays an important part in the interaction of molecular orbitals, such that the orbitals only interact with ones with the same symmetry.
The endo and exo transition states in a Diels-Alder reaction were also studied, and it was found that generally in a Diels-Alder reaction, the endo transition state is kinetically favourable due to secondary orbital interactions, while the exo transition state is thermodynamically favourable due to less steric hindrance.
The reaction between xylylene and SO2 poses an exception, where a possible cheletropic reaction yields the most thermodynamically favourable product. Therefore, under thermodynamic control, the reaction would not produce an exo Diels-Alder product, but instead a cheletropic product.
References
- ↑ 1.0 1.1 P.W. Atkins, Atkins' Physical Chemistry, W.H. Freeman, New York, 8th edn., 2006.
- ↑ J.M. Berg, J. L. Tymoczko, L. Stryer, in Biochemistry., W.H. Freeman, New York, 5th edn., 2002, Appendix C: Standard Bond Lengths, https://www.ncbi.nlm.nih.gov/books/NBK21220/, (accessed 1st November, 2016).
- ↑ A. Bondi, J. Phys. Chem., 1964, 68 (3), 441-451.
