Jump to content

Rep:Mod:mb3210

From ChemWiki

Introduction

This computational chemistry course aims at giving an insight into bonding and chemical structure of molecules. Gaussview 5.0.9 linked to the Gaussian software was used to carry out calculations.

Week 1 consists of understanding the Gaussview 5.0.9 software and learning how to carry out calculations. This involves the optimisation, frequency analysis and molecular orbital analysis of a range of molecules, including BH3, TlBr3 and NH3. Kinetic and thermodynamic properties of the molecule can then be determined. When Gaussian carries out an optimisation, firstly, the nuclei are assumed to have fixed positions relative to the electrons (Born-Oppenheimer Approx), then the Schrödinger equation is solved with respect to the electrons, namely the SCF part of the calculation. Secondly, the Schrödinger equation is then solved for the position of the nuclei, namely the OPT part of the calculation (much more time consuming part of the calculation). The optimised molecule is the one with the lowest energy geometry from the calculations.

Week 2 is a mini-project where the techniques learnt from the previous week can be applied to further our understanding on the topic and cement our working knowledge of Gaussview 5.0. Additionally, the calculated data can be compared to experimental data as a way of judging the accuracy of experimental methods.

Optimising a molecule [Week 1]

Optimising a molecule of BH3

A borane molecule was created on Gaussview 5.0.9 with a trigonal planar structure and the bond lengths set to 1.5Å. The molecule was then optimised using a 3-21G basis set and the RB3LYP calculation method. The basis set determines the accuracy of the calculation, with 3-21G having very low accuracy but with the advantage of being a fast calculation. A 6-31G basis set for example is more accurate but more time consuming. The outcome is published below.

A Gaussview image of an optimised borane molecule

Jmol

Optimised B-H bond distance: 1.19Å
Optimised H-B-H bond angle: 120.0°

File:BH3 OPT 321G mb3210.LOG

Calculation summary
Parameters
File Type .log
Calculation Type FOPT
Calculation Method RB3LYP
Basis Set 3-21G
Charge 0
Spin Singlet
Total energy(a.u.) -26.46226338
RMS Gradient(a.u.) 0.00020672
Dipole Moment(Debye) 0.00
Point Group D3h
Time taken 18.0 seconds 


 Item               Value     Threshold  Converged?
 Maximum Force            0.000413     0.000450     YES
 RMS     Force            0.000271     0.000300     YES
 Maximum Displacement     0.001610     0.001800     YES
 RMS     Displacement     0.001054     0.001200     YES
 Predicted change in Energy=-1.071764D-06
 Optimization completed.
    -- Stationary point found.
                           ----------------------------
                           !   Optimized Parameters   !
                           ! (Angstroms and Degrees)  !
 --------------------------                            --------------------------
 ! Name  Definition              Value          Derivative Info.                !
 --------------------------------------------------------------------------------
 ! R1    R(1,2)                  1.1935         -DE/DX =    0.0004              !
 ! R2    R(1,3)                  1.1935         -DE/DX =    0.0004              !
 ! R3    R(1,4)                  1.1935         -DE/DX =    0.0004              !
 ! A1    A(2,1,3)              120.0            -DE/DX =    0.0                 !
 ! A2    A(2,1,4)              120.0            -DE/DX =    0.0                 !
 ! A3    A(3,1,4)              120.0            -DE/DX =    0.0                 !
 ! D1    D(2,1,4,3)            180.0            -DE/DX =    0.0                 !
 --------------------------------------------------------------------------------

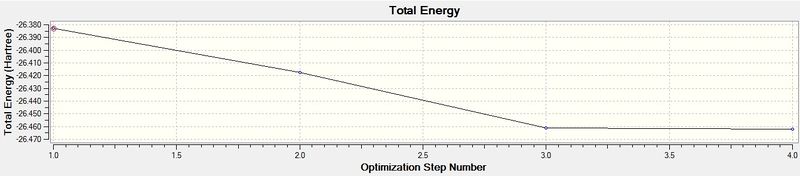
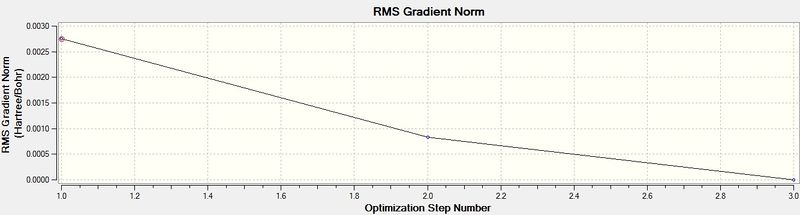
The above table is proof that the optimisation of the molecule was completed successfully, since it says "YES" under the "Converged?" heading. The RMS gradient is tending towards zero (less than 0.001), as seen in the graph below, which is also indicative of successful optimisation of a molecule, as well noticing that the B-H bond-length has decreased from the pre-set distance of 1.50Å, to an optimised distance of 1.19Å.

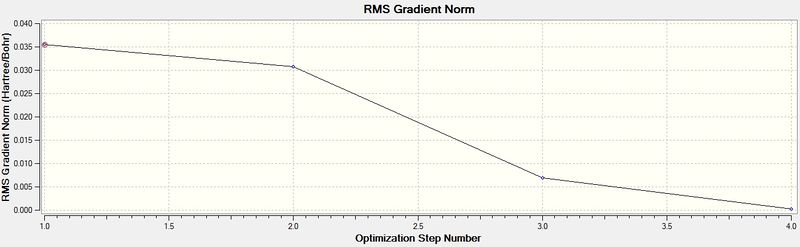
RMS gradient graph of BH3 produced in Gaussview













The energy graph is also shown below which further shows the optimisation tends to a more negative energy

Total energy graph of BH3 produced in Gaussview
A Gaussview animation of optimisation of a borane molecule











The animation on the left show the optimisation structures. The structure where the B-H bond distance is at its smallest corresponds to the most negative energy in the optimisation plot and the smallest RMS gradient. Hence, this is the most stable structure found and is the optimised structure of the molecule. It will adopt this structure in the gas phase as well as in the solid state providing no solid state forces act to distort the molecule. It is also worth noticing that in the first step of the optimisation, the bonds connecting the atoms seem to disappear. However, this is not the case and the bonds between the atoms do still exist, rather the Gaussian software only draws bonds within a pre-defined distance separating the atoms. This is because in reality, bonds are not fixed lines joining two atoms, but instead should be viewed as an electrostatic force of attraction between the opposing charges of protons and electrons. Hence, a bond increases in strength as two atoms approach each other from infinite distance, not, as Gaussview suggests, that a bond is suddenly formed at a set distance. A potential energy curve of two atoms based on internuclear separation is a good illustration of this point.







Using a better basis set for BH3

The borane molecule optimised with the 3-21G basis set was further optimised using the more accurate 6-31G basis set. Again, the RB3LYP calculation method was applied. The results are published below.

A Gaussview image of an optimised borane molecule

Jmol

Optimised B-H bond distance: 1.19Å
Optimised H-B-H bond angle: 120.0°

File:BH3 OPT 631G MB3210.LOG

Calculation summary
Parameters
File Type .log
Calculation Type FOPT
Calculation Method RB3LYP
Basis Set 6-31G(d,p)
Charge 0
Spin Singlet
Total energy(a.u.) -26.61532363
RMS Gradient(a.u.) 0.00000235
Dipole Moment(Debye) 0.00
Point Group D3h
Time taken 13.0 seconds 
Item               Value     Threshold  Converged?
 Maximum Force            0.000005     0.000450     YES
 RMS     Force            0.000003     0.000300     YES
 Maximum Displacement     0.000019     0.001800     YES
 RMS     Displacement     0.000012     0.001200     YES
 Predicted change in Energy=-1.304899D-10
 Optimization completed.
    -- Stationary point found.
                           ----------------------------
                           !   Optimized Parameters   !
                           ! (Angstroms and Degrees)  !
 --------------------------                            --------------------------
 ! Name  Definition              Value          Derivative Info.                !
 --------------------------------------------------------------------------------
 ! R1    R(1,2)                  1.1923         -DE/DX =    0.0                 !
 ! R2    R(1,3)                  1.1923         -DE/DX =    0.0                 !
 ! R3    R(1,4)                  1.1923         -DE/DX =    0.0                 !
 ! A1    A(2,1,3)              120.0            -DE/DX =    0.0                 !
 ! A2    A(2,1,4)              120.0            -DE/DX =    0.0                 !
 ! A3    A(3,1,4)              120.0            -DE/DX =    0.0                 !
 ! D1    D(2,1,4,3)            180.0            -DE/DX =    0.0                 !
 --------------------------------------------------------------------------------

A difference in energy can be seen between the two basis sets used, however, we cannot compare them since they were computed using different basis sets. Only those calculations performed using the same basis sets and containing the same number of atoms can be compared.

Using pseudo-potentials and larger basis sets

Pseudo potentials: TlBr3

Heavy atoms such as thallium and bromine require the use of pseudo potentials which requires the basis set to be LanL2DZ. This is a medium level basis set where D95V is used on first row atoms and Los Alamos ECP on heavier elements. Once more, the RB3LYP calculation method was employed. One of the major advantages here of computing a molecule containing thallium, is we can understand some of its thermodynamic and kinetic properties without being exposed to the risks that thallium presents. The calculation method was set to RB3LYP and the point group constrained to D3H with a very tight tolerance (0.0001).

A Gaussview image of an optimised Thallium tribromide molecule

Jmol

Optimised Tl-Br bond distance: 2.65Å
Optimised Br-Tl-Br bond angle: 120.0°

Dspace:http://hdl.handle.net/10042/22471

File:TlBr3 OPT LanL2DZ mb3210.LOG

Calculation summary
Parameters
File Type .log
Calculation Type FOPT
Calculation Method RB3LYP
Basis Set LANL2DZ
Charge 0
Spin Singlet
Total energy(a.u.) -91.21812851
RMS Gradient(a.u.) 0.00000090
Dipole Moment(Debye) 0.00
Point Group D3h
Time taken 34.9 seconds 
 Item               Value     Threshold  Converged?
 Maximum Force            0.000002     0.000450     YES
 RMS     Force            0.000001     0.000300     YES
 Maximum Displacement     0.000022     0.001800     YES
 RMS     Displacement     0.000014     0.001200     YES
 Predicted change in Energy=-6.084044D-11
 Optimization completed.
    -- Stationary point found.
                           ----------------------------
                           !   Optimized Parameters   !
                           ! (Angstroms and Degrees)  !
 --------------------------                            --------------------------
 ! Name  Definition              Value          Derivative Info.                !
 --------------------------------------------------------------------------------
 ! R1    R(1,2)                  2.651          -DE/DX =    0.0                 !
 ! R2    R(1,3)                  2.651          -DE/DX =    0.0                 !
 ! R3    R(1,4)                  2.651          -DE/DX =    0.0                 !
 ! A1    A(2,1,3)              120.0            -DE/DX =    0.0                 !
 ! A2    A(2,1,4)              120.0            -DE/DX =    0.0                 !
 ! A3    A(3,1,4)              120.0            -DE/DX =    0.0                 !
 ! D1    D(2,1,4,3)            180.0            -DE/DX =    0.0                 !
 --------------------------------------------------------------------------------
A Gaussview animation of optimisation of a Thalium tribromide molecule

The optimisation animation of TlBr3 shows the structure where the bond lengths are optimised at the shortest distance to give the most negative energy and smallest RMS gradient.

RMS gradient graph of TlBr3 produced in Gaussview












The energy graph is also shown below which further shows the optimisation tends to a more negative energy

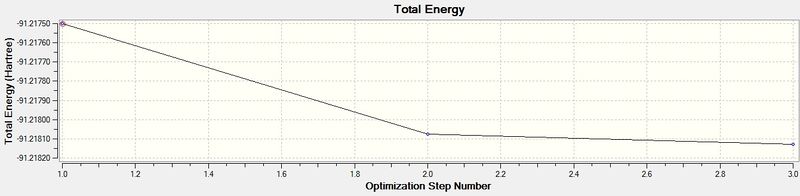
Total energy graph of TlBr3 produced in Gaussview











The calculated bond length is 2.65Å and experimentally the Tl-Br bond length in TlBr3 has been found to be 2.51Å.[1] This gives an error of 5.24% which can be attributed to the approximations used in the basis set for the calculations. A better basis set could have been chosen to optimise the bond lengths further, however, when selecting a basis set, it is important to consider whether choosing a better basis set outweighs a more time consuming process needed for the calculation.

Using a mixture of basis sets and pseudo-potentials: BBr3

The optimisation was carried out using the RB3LYP calculation method and the point group constrained to D3H with very tight tolerance (0.0001). The basis set used was Gen.

A Gaussview image of an optimised Boron tribromide molecule

Jmol

Optimised B-Br bond distance: 1.93Å
Optimised Br-B-Br bond angle: 120.0°

Dspace:http://hdl.handle.net/10042/22470

File:BBr3 OPT GEN MB3210.LOG

Calculation summary
Parameters
File Type .log
Calculation Type FOPT
Calculation Method RB3LYP
Basis Set Gen
Charge 0
Spin Singlet
Total energy(a.u.) -64.43645296
RMS Gradient(a.u.) 0.00000382
Dipole Moment(Debye) 0.00
Point Group D3h
Time taken 31.8 seconds 
Item               Value     Threshold  Converged?
 Maximum Force            0.000008     0.000450     YES
 RMS     Force            0.000005     0.000300     YES
 Maximum Displacement     0.000036     0.001800     YES
 RMS     Displacement     0.000023     0.001200     YES
 Predicted change in Energy=-4.026911D-10
 Optimization completed.
    -- Stationary point found.
                           ----------------------------
                           !   Optimized Parameters   !
                           ! (Angstroms and Degrees)  !
 --------------------------                            --------------------------
 ! Name  Definition              Value          Derivative Info.                !
 --------------------------------------------------------------------------------
 ! R1    R(1,2)                  1.934          -DE/DX =    0.0                 !
 ! R2    R(1,3)                  1.934          -DE/DX =    0.0                 !
 ! R3    R(1,4)                  1.934          -DE/DX =    0.0                 !
 ! A1    A(2,1,3)              120.0            -DE/DX =    0.0                 !
 ! A2    A(2,1,4)              120.0            -DE/DX =    0.0                 !
 ! A3    A(3,1,4)              120.0            -DE/DX =    0.0                 !
 ! D1    D(2,1,4,3)            180.0            -DE/DX =    0.0                 !
 --------------------------------------------------------------------------------
A Gaussview animation of optimisation of a Boron tribromide molecule

As before, the optimisation animation shows the shortest bond length which gives an optimised structure to give the most negative energy and the smallest RMS gradient.

RMS gradient graph of BBr3 produced in Gaussview












The energy graph is also shown below which further shows the optimisation tends to a more negative energy

Total energy graph of BBr3 produced in Gaussview












Comparison of computed bond lengths on optimised structures of BH3 , TlBr3 and BBr3

Calculated bond lengths in BH3 , TlBr3 and BBr3
Bond Calculated Bond Length (Å) Experimental Bond Length (Å) Basis Set
B-H 1.19 1.08 (in hexamethylenetetramine-borine)[2] 6-31G(d,p)
Tl-Br 2.65 2.51[1] LanL2DZ
B-Br 1.93 2.01[3] Gen

The above data shows how bond lengths differ depending on the size of the atoms involved, and hence how the orbital overlap varies. Comparison of the B-H bond (1.19Å) with the B-Br bond (1.93Å) shows that the presence of the larger Br atom compared to H results in a much longer bond. Despite the greater electronegativity difference in B-Br than B-H, there is poorer orbital overlap in B-Br since the size of the atoms differ greatly and the Br orbitals are more diffuse. In B-H however, the atoms are of similar size, so the overlap is greater. Hence, the bond in B-Br is weaker and therefore longer.

Likewise, a comparison can be made between the Tl-Br bond length (2.65Å) and that of B-Br (1.93Å). Thallium is in the same group as Boron, but four periods below. Therefore, a useful comparison can be drawn by examining the effect on bond length when changing the Group 13 atom. Br is two periods above Tl and two periods below B. Tl is a large atom in the 6th period of the periodic table, hence its valence shell is far more diffuse than that of Boron. Therefore, the overlap of the orbitals in B and Br is far greater than that in Tl and Br. As a result, the B-Br bond is shorter and stronger than Tl-Br.

Experimental data shows similar bond lengths to those calculated and limitations of experimental techniques can account for the differences.

Frequency analysis

BH3

File:BH3 FREQ MB3210.LOG

Calculation summary
Parameters
File Type .log
Calculation Type FREQ
Calculation Method RB3LYP
Basis Set 6-31G(d,p)
Charge 0
Spin Singlet
Total energy(a.u.) -26.61532363
RMS Gradient(a.u.) 0.00000237
Dipole Moment(Debye) 0.00
Point Group D3h
Time taken 11.0 seconds 
Item               Value     Threshold  Converged?
 Maximum Force            0.000005     0.000450     YES
 RMS     Force            0.000002     0.000300     YES
 Maximum Displacement     0.000019     0.001800     YES
 RMS     Displacement     0.000009     0.001200     YES
 Predicted change in Energy=-1.323374D-10
 Optimization completed.
    -- Stationary point found.
Low frequencies ---   -0.9033   -0.7343   -0.0054    6.7375   12.2491   12.2824
Low frequencies --- 1163.0003 1213.1853 1213.1880

We know there should be 3N-6 vibrational frequencies present. For BH3, N=4 so we can expect 6 vibrations as the frequency table shows below. However, in the infrared spectrum also shown below, only 3 peaks are present. This can be explained by considering the symmetry of the vibrations. Firstly. vibrational mode 4 is totally symmetric, displaying A'1 symmetry. As a result it is infrared inactive. From the remaining 5 vibrational modes, there is one pair of degenerate vibrations at 1213 cm-1 with E' symmetry, one pair at 2715 cm-1 also with E' symmetry and one mode at 1163 cm-1 with A' '2 symmetry. Hence, there are three distinct vibrations.

Infrared spectrum of BH3 produced in Gaussview

















Frequency analysis of BH3
No. Form of vibration Frequency(cm-1) Intensity Symmetry D3h point group
1 All H atoms move together in a concerted motion up and down in the plane of the principal axis. The B atom moves up and down the same plane, but in the opposite direction to the H atoms. This causes a distinct change in dipole moment 1163 93 A' '2
2 One of the H atoms remains in a fixed position in relation to the B atom, while the other two H atoms bend towards each other in the plane perpendicular to the principal axis (In-plane scissoring) 1213 14 E'
3 For two hydrogens, the H-B-H bond angle remains constant and the atoms bend clockwise together. The third H atom moves towards and away from each other H atom in turn (Asymmetric scissoring) 1213 14 E'
4 B atom stationary, all H atoms move in and out in the plane of a B-H bond together in a concerted motion (In-plane symmetric stretching) 2582 0 A '1
5 For one H atom, the B-H bond remains fixed, while for the other two H atoms the B-H bond shortens and lengthens equal and opposite amounts to each other (Asymmetric stretching) 2715 126 E'
6 For two H atoms, the B-H bonds shorten and lengthen equally together, while the other B-H bond lengthens when the other two B-H bonds shorten and vice versa (2 hydrogens stretching symmetrically in-phase, one stretching of out phase) 2715 126 E'


Vibrations of BH3
Frequency vibration no.
1 2 3 4 5 6
Animation
Vibration
Vibration
Vibration
Vibration
Vibration
Vibration

TlBr3

Dspace:http://hdl.handle.net/10042/22450

File:TlBr3 FREQ MB3210.LOG

Calculation summary
Parameters
File Type .log
Calculation Type FREQ
Calculation Method RB3LYP
Basis Set LANL2DZ
Charge 0
Spin Singlet
Total energy(a.u.) -91.21812851
RMS Gradient(a.u.) 0.00000088
Imaginary Freq 0
Dipole Moment(Debye) 0.00
Point Group D3h
Time taken 25.2 seconds 
Item               Value     Threshold  Converged?
 Maximum Force            0.000002     0.000450     YES
 RMS     Force            0.000001     0.000300     YES
 Maximum Displacement     0.000022     0.001800     YES
 RMS     Displacement     0.000011     0.001200     YES
 Predicted change in Energy=-5.660901D-11
 Optimization completed.
    -- Stationary point found.
Low frequencies ---   -3.4213   -0.0026   -0.0004    0.0015    3.9367    3.9367
Low frequencies ---   46.4289   46.4292   52.1449


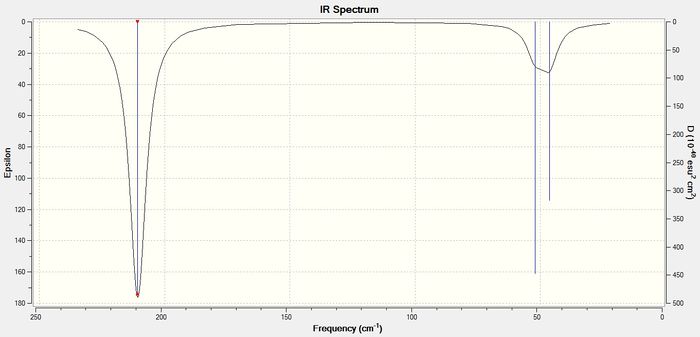
Infrared spectrum of TlBr3 produced in Gaussview

















Similarly to BH3, the infrared spectrum of TlBr3 shows 3 peaks. These are at 46 cm-1 (lowest "real" normal mode), which corresponds to vibrational modes 1 and 2, 52 cm-1 corresponding to vibration 3 and at 211 cm-1 which represents vibrations 5 and 6. Vibrational mode 4 has no peak in the infrared spectrum since it is totally symmetric and therefore infrared inactive.



Frequency analysis of TlBr3
No. Form of vibration Frequency(cm-1) Intensity Symmetry D3h point group
1 One of the Br atoms remains in a fixed position in relation to the Tl atom, while the other two Br atoms bend towards each other in the plane perpendicular to the principal axis (In-plane scissoring) 46 4 E'
2 For two hydrogens, the Br-Tl-Br bond angle remains constant and the atoms bend clockwise together. The third Br atom moves towards and away from each other Br atom in turn (Asymmetric scissoring) 46 4 E'
3 All Br atoms move together in a concerted motion up and down in the plane of the principal axis. The Tl atom moves up and down the same plane, but in the opposite direction to the Br atoms. This causes a distinct change in dipole moment 52 6 A' '2
4 Tl atom stationary, all Br atoms move in and out in the plane of a Tl-Br bond together in a concerted motion (In-plane symmetric scissoring) 165 0 A '1
5 For one Br atom, the Tl-Br bond remains fixed, while for the other two H atoms the Tl-Br bond shortens and lengthens equal and opposite amounts to each other (Asymmetric scissoring) 211 25 E'
6 For two Br atoms, the Tl-Br bonds shorten and lengthen equally together, while the other Tl-Br bond lengthens when the other two Tl-Br bonds shorten and vice versa (2 bromine atoms stretching symmetrically in-phase, one stretching of out phase) 211 25 E'


Vibrations of TlBr3
Frequency vibration no.
1 2 3 4 5 6
Animation
Vibration
Vibration
Vibration
Vibration
Vibration
Vibration

Comparison of vibrational frequencies of TlBr3 and TlBr3

Vibrational frequencies in TlBr3 and BH3
Vibrational frequencies (cm-1)
TlBr3 BH3
46 1163
46 1213
52 1213
165 2582
211 2715
211 2715

The first obvious comparison to be made is that the vibrational frequencies in BH3 are two orders of magnitude larger than in TlBr3. This can be attributed to the greater bond strength in the B-H bond in comparison to the Tl-Br bond and is in accordance with the significantly shorter B-H bond length. We can invoke the same argument as used in the comparison of bond lengths. The more diffuse orbitals in the Tl-Br bond results in poorer orbital overlap, a weaker bond and hence a lower vibrational frequency. Another approach to explaining the lower vibrational frequency in TlBr3 is to consider Hooke's Law. This relates the vibrational frequency of a molecule to its redcued mass. Hence, the larger the two atoms, the greater their reduced mass, so the lower their vibrational frequency. It is worth noting that whilst each molecule has 6 vibrational modes, the ordering differs slightly between the two. Similarly, the infrared spectra for each molecule show three peaks, relating to the two being isostructural. In BH3, the ordering is A' ' 2, E', E', A'1, E', E' whereas in TlBr3 it is E', E', A' '2, A'1, E', E'. However, for both, the A'1 and E' vibrations are close in energy, while the A' '2 and the other set of E' vibrations are also energetically close. In BH3, the first 3 modes are bending frequencies whilst the other 3 modes are stretching frequencies which could explain the similarities in their vibrational frequencies. The same can be said for TlBr3.

It is important to note that if any comparison is to be attempted between calculations that they use the same method basis set for optimisation and frequency analysis. Calculations using a different basis set are not comparable and no conclusions can be drawn. The purpose of carrying out a frequency analysis is to confirm that the optimised structure obtained is a minimum. It is also very useful in analysing and understanding the vibrational modes in molecules and helps in the interpretation of infrared spectra. The "low frequencies" found in the .log file represent the "-6" part in the equation for the number of vibrational modes, "3N-6", and are representative of the motions of the centre of mass of the molecule.

Molecular orbital analysis

Population analysis of BH3

Dspace:http://hdl.handle.net/10042/22469

File:BH3 NBO MB3210.log

Calculation summary
Parameters
File Type .log
Calculation Type SP
Calculation Method RB3LYP
Basis Set 6-31G(d,p)
Charge 0
Spin Singlet
Total energy(a.u.) -26.61532363
Dipole Moment(Debye) 0.00
Point Group D3h
Time taken 16 minutes 21.0 seconds
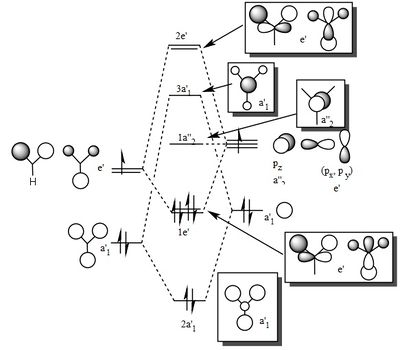
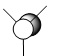
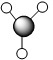
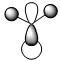
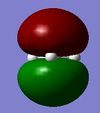
Molecular orbital diagram of BH3 using a Linear Combination of Atomic Orbitals
Comparison of "real" MOs produced in Gaussview vs "LCAO" MOs produced on Chemdraw for BH3
Method 1 2 3 4 5 6 7
LCAO
Real
Symmetry label a'1 e' e' a2 a'1 e' e'

From the comparison table above, it is easy to see that the LCAO method for constructing MOs produces a very good fit in comparison to the calculated "Real" MOs in Gaussview. Hence, the LCAO approach proves that qualitative MO theory can be used for accurate modelling of MOs for small, simple molecules.



NBO Analysis

NH3

Optimisation

The optimisation of NH3 was carried out in Gaussview using the RB3LYP calculation method and a 6-31G basis set, applying the "nosymm" keyword. The summary data is shown below.

File:NH3 OPT 631G MB3210.log

Calculation summary
Parameters
File Type .log
Calculation Type FOPT
Calculation Method RB3LYP
Basis Set 6-31G(d,p)
Charge 0
Spin Singlet
Total energy(a.u.) -56.55776856
RMS Gradient(a.u.) 0.00000885
Dipole Moment(Debye) 1.85
Point Group C1
Time taken 18.0 seconds

Optimised N-H bond distance: 1.02Å
Optimised H-N-H bond angle: 105.7° 

Item               Value     Threshold  Converged?
 Maximum Force            0.000024     0.000450     YES
 RMS     Force            0.000012     0.000300     YES
 Maximum Displacement     0.000079     0.001800     YES
 RMS     Displacement     0.000053     0.001200     YES
 Predicted change in Energy=-1.629728D-09
 Optimization completed.
    -- Stationary point found.


Frequency analysis

File:NH3 FREQ MB3210.log

Calculation summary
Parameters
File Type .log
Calculation Type FREQ
Calculation Method RB3LYP
Basis Set 6-31G(d,p)
Charge 0
Spin Singlet
Total energy(a.u.) -56.55776856
RMS Gradient(a.u.) 0.00000878
Dipole Moment(Debye) 1.85
Point Group C1
Time taken 9.0 seconds 
 Item               Value     Threshold  Converged?
 Maximum Force            0.000007     0.000450     YES
 RMS     Force            0.000003     0.000300     YES
 Maximum Displacement     0.000021     0.001800     YES
 RMS     Displacement     0.000009     0.001200     YES
 Predicted change in Energy=-6.353265D-11
 Optimization completed.
    -- Stationary point found.
Low frequencies ---  -31.6906   -0.0009    0.0003    0.0006   13.0070   25.5725
 Low frequencies --- 1089.5009 1694.1085 1694.1682


Population analysis

File:NH3 NBO MB3210.log

Calculation summary
Parameters
File Type .log
Calculation Type SP
Calculation Method RB3LYP
Basis Set 6-31G(d,p)
Charge 0
Spin Singlet
Total energy(a.u.) -56.55776856
Dipole Moment(Debye) 1.85
Point Group C1
Time taken 8 minutes 8.3 seconds

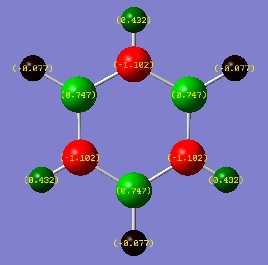
NBO analysis of NH3

A Gaussview image of the charge distribution in NH3


Charge range of NH3


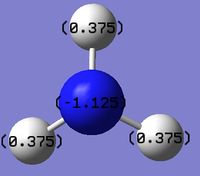
The charge range can be seen above and is -1.125 to +1.125

The NBO charges were then shown using Gaussview:


Nitrogen NBO charge = -1.125
Hydrogen NBO charge = +0.375

A Gaussview image of NBO charge in NH3


NH3BH3 dissociation energy analysis

Optimisation

3-21G basis set

The initial optimisation was carried out using a 3-21G basis set and RB3LYP calculation method.

Dspace:http://hdl.handle.net/10042/22502

File:NH3BH3 OPT 321G MB3210.log

Calculation summary
Parameters
File Type .log
Calculation Type FOPT
Calculation Method RB3LYP
Basis Set 3-21G
Charge 0
Spin Singlet
Total energy(a.u.) -82.76661837
RMS Gradient(a.u.) 0.00003006
Dipole Moment(Debye) 5.84
Point Group C1
Time taken 59.4 seconds 
Item               Value     Threshold  Converged?
 Maximum Force            0.000094     0.000450     YES
 RMS     Force            0.000030     0.000300     YES
 Maximum Displacement     0.000419     0.001800     YES
 RMS     Displacement     0.000178     0.001200     YES
 Predicted change in Energy=-5.742846D-08
 Optimization completed.
    -- Stationary point found.

6-31G(d,p) basis set

The optimisation was then carried out using the more accurate 6-31G(d,p) basis set and a RB3LYP calculation method.

Dspace:http://hdl.handle.net/10042/22503

File:NH3BH3 OPT 631G MB3210.log

Calculation summary
Parameters
File Type .log
Calculation Type FOPT
Calculation Method RB3LYP
Basis Set 6-31G(d,p)
Charge 0
Spin Singlet
Total energy(a.u.) -83.22469001
RMS Gradient(a.u.) 0.00005640
Dipole Moment(Debye) 5.56
Point Group C1
Time taken 59.1 seconds 
Item               Value     Threshold  Converged?
 Maximum Force            0.000132     0.000450     YES
 RMS     Force            0.000037     0.000300     YES
 Maximum Displacement     0.001235     0.001800     YES
 RMS     Displacement     0.000549     0.001200     YES
 Predicted change in Energy=-1.183236D-07
 Optimization completed.
    -- Stationary point found.

Frequency analysis

Dspace:http://hdl.handle.net/10042/22504

File:NH3BH3 FREQ MB3210.log

Calculation summary
Parameters
File Type .log
Calculation Type FREQ
Calculation Method RB3LYP
Basis Set 6-31G(d,p)
Charge 0
Spin Singlet
Total energy(a.u.) -83.22469001
RMS Gradient(a.u.) 0.00005643
Dipole Moment(Debye) 5.56
Point Group C1
Time taken 57.0 seconds 
Item               Value     Threshold  Converged?
 Maximum Force            0.000254     0.000450     YES
 RMS     Force            0.000056     0.000300     YES
 Maximum Displacement     0.001414     0.001800     YES
 RMS     Displacement     0.000702     0.001200     YES
 Predicted change in Energy=-2.149394D-07
 Optimization completed.
    -- Stationary point found.
Low frequencies ---   -0.0011   -0.0008    0.0008    6.6382   14.5267   20.1742
 Low frequencies ---  263.3505  631.3096  638.0440

Dissociation energy

E(NH3): -56.55776856
E(BH3): -26.61532363
E(NH3BH3): -83.22469001

Energy difference: ΔE=E(NH3BH3)-[E(NH3)+E(BH3)]
Hence, ΔE= (-83.22469001)-[(-56.55776856)+(-26.61532363)]
ΔE= -0.05159782 a.u.

Therefore, Edissociation= -135.47 kJmol-1

Mini Project [Week 2] - Aromaticity


All calculations hereafter were performed on the HPC servers using a calculation method of RB3LYP and a 6-31G(d,p) basis set.


Benzene

Optimisation

Gaussview image of benzene

Dspace: http://hdl.handle.net/10042/22512
File:Benzene OPT 631G mb3210.log

Calculation summary
Parameters
File Type .log
Calculation Type FOPT
Calculation Method RB3LYP
Basis Set 6-31G(d,p)
Charge 0
Spin Singlet
Total energy(a.u.) -232.25821387
RMS Gradient(a.u.) 0.00008450
Dipole Moment(Debye) 0.00
Point Group D6H
Time taken 1 minute 3.7 seconds

Optimised C-C bond length: 1.40Å
Optimised C-H bond length: 1.09Å

Item               Value     Threshold  Converged?
 Maximum Force            0.000199     0.000450     YES
 RMS     Force            0.000081     0.000300     YES
 Maximum Displacement     0.000847     0.001800     YES
 RMS     Displacement     0.000299     0.001200     YES
 Predicted change in Energy=-4.636830D-07
 Optimization completed.
    -- Stationary point found.

Frequency analysis

Dspace: http://hdl.handle.net/10042/22513
File:Benzene FREQ mb3210.log

Calculation summary
Parameters
File Type .log
Calculation Type FREQ
Calculation Method RB3LYP
Basis Set 6-31G(d,p)
Charge 0
Spin Singlet
Total energy(a.u.) -232.25821387
RNS Gradient(a.u.) 0.00008452
Imaginary Freq 1
Dipole Moment(Debye) 0.00
Point Group D6H
Time taken 1 minute 28.9 seconds 
Item               Value     Threshold  Converged?
 Maximum Force            0.000199     0.000450     YES
 RMS     Force            0.000085     0.000300     YES
 Maximum Displacement     0.000806     0.001800     YES
 RMS     Displacement     0.000346     0.001200     YES
 Predicted change in Energy=-4.349367D-07
 Optimization completed.
    -- Stationary point found.
Low frequencies ---   -4.6046   -4.6046   -0.0088   -0.0043   -0.0042    9.6590
 Low frequencies ---  413.9386  413.9386  621.1428

Population analysis

Dspace: http://hdl.handle.net/10042/22540
File:Benzene NBO mb3210.log

Calculation summary
Parameters
File Type .log
Calculation Type SP
Calculation Method RB3LYP
Basis Set 6-31G(d,p)
Charge 0
Spin Singlet
Total energy(a.u.) -232.25821387
Dipole Moment(Debye) 0.00
Point Group D6H
Time taken 54.1 seconds

MO diagram

The benzene molecular orbital diagram shown below shows the "centre" part of the molecular orbitals present in benzene, ranging from MOs 7 to 32 (7-21 occupied, 22-32 unoccupied) in Gaussview. The MO diagram starts with all bonding s orbitals, going through to all bonding p orbitals, finishing with anti-bonding generate MOs composed of s orbitals. There are many more MOs calculated in Gaussview, however, these soon become very complex to interpret and move away from the LCAO. The symmetry of each MO was determined to assist in identifying degernate MOs (can be found in the .log file).

LCAO MO diagram of benzene

The concept of aromaticity can be easily represented in benzene. For a molecule to be aromatic, it must follow Hückel's rule that an aromatic molecule contains 4n+2 π electrons, where n is an integer. Benzene has 6π electrons, hence n=2, so benzene conforms to Hückel's rule. Likewise, both pyridinium and boratabenzene also contain 6π electrons due to their respective charges offsetting the difference in valence electrons between carbon and both nitrogen and boron. Hence, they too are aromatic molecules. Pyridinium derivatives, such as pyridinium chlorochromate, have beneficial uses, being used as a mild oxidating agent for converting alcohols to carbonyl compounds.[4] Borazine, on the other hand, has a long history focusing on its aromaticity, being the subject of much debate. It can be described as a π aromatic compound, but it is not globally aromatic as the electronic system is not as delocalised as in benzene.[5] Therefore, it is still considered aromatic and is often referred to as "inorganic benzene".[5]

Pyridinium

Optimisation

Gaussview image of pyridinium

Dspace: http://hdl.handle.net/10042/22515
File:Pyridinium OPT 631G mb3210.log

Calculation summary
Parameters
File Type .log
Calculation Type FOPT
Calculation Method RB3LYP
Basis Set 6-31G(d,p)
Charge 1
Spin Singlet
Total energy(a.u.) -248.66807395
RMS Gradient(a.u.) 0.00003889
Dipole Moment(Debye) 1.87
Point Group C2V
Time taken 1 minute 52.4 seconds

Optimised N-C bond length: 1.35Å
Optimised N-H bond length: 1.02Å

Item               Value     Threshold  Converged?
 Maximum Force            0.000063     0.000450     YES
 RMS     Force            0.000023     0.000300     YES
 Maximum Displacement     0.000698     0.001800     YES
 RMS     Displacement     0.000178     0.001200     YES
 Predicted change in Energy=-7.097421D-08
 Optimization completed.
    -- Stationary point found.

Frequency analysis

Dspace: http://hdl.handle.net/10042/22516
File:Pyridinium FREQ mb3210.log

Calculation summary
Parameters
File Type .log
Calculation Type FREQ
Calculation Method RB3LYP
Basis Set 6-31G(d,p)
Charge 1
Spin Singlet
Total energy(a.u.) -248.66807395
RMS Gradient(a.u.) 0.00003891
Dipole Moment(Debye) 1.87
Point Group C2V
Time taken 2 minutes 27.7 seconds 
Item               Value     Threshold  Converged?
 Maximum Force            0.000155     0.000450     YES
 RMS     Force            0.000039     0.000300     YES
 Maximum Displacement     0.000758     0.001800     YES
 RMS     Displacement     0.000231     0.001200     YES
 Predicted change in Energy=-7.607867D-08
 Optimization completed.
    -- Stationary point found.
Low frequencies ---   -7.2529   -0.0006    0.0009    0.0010   17.3499   18.5758
 Low frequencies ---  392.4576  404.0624  620.4718

Population analysis

Dspace: http://hdl.handle.net/10042/22541
File:Pyridinium NBO mb3210.log

Calculation summary
Parameters
File Type .log
Calculation Type SP
Calculation Method RB3LYP
Basis Set 6-31G(d,p)
Charge 1
Spin Singlet
Total energy(a.u.) -248.66807395
Dipole Moment(Debye) 1.87
Point Group C2V
Time taken 58.1 seconds

Boratabenzene

Optimisation

Gaussview image of boratabenzene

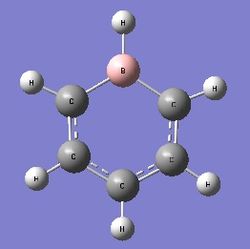
Dspace: http://hdl.handle.net/10042/22517
File:Boratabenzene OPT 631G mb3210.log

Calculation summary
Parameters
File Type .log
Calculation Type FOPT
Calculation Method RB3LYP
Basis Set 6-31G(d,p)
Charge -1
Spin Singlet
Total energy(a.u.) -219.02052980
RMS Gradient(a.u.) 0.00016432
Dipole Moment(Debye) 2.85
Point Group C2V
Time taken 1 minute 54.6 seconds

Optimised B-H bond length: 1.22Å
Optimised B-C bond length: 1.51Å


Item               Value     Threshold  Converged?
 Maximum Force            0.000158     0.000450     YES
 RMS     Force            0.000071     0.000300     YES
 Maximum Displacement     0.000914     0.001800     YES
 RMS     Displacement     0.000329     0.001200     YES
 Predicted change in Energy=-6.959555D-07
 Optimization completed.
    -- Stationary point found.

Frequency analysis

Dspace: http://hdl.handle.net/10042/22518
File:Boratabenzene FREQ mb3210.log

Calculation summary
Parameters
File Type .log
Calculation Type FREQ
Calculation Method RB3LYP
Basis Set 6-31G(d,p)
Charge -1
Spin Singlet
Total energy(a.u.) -219.02052979
RMS Gradient(a.u.) 0.00016443
Dipole Moment(Debye) 2.85
Point Group C2V
Time taken 2 minutes 30.3 seconds 
Item               Value     Threshold  Converged?
 Maximum Force            0.000434     0.000450     YES
 RMS     Force            0.000164     0.000300     YES
 Maximum Displacement     0.000889     0.001800     YES
 RMS     Displacement     0.000398     0.001200     YES
 Predicted change in Energy=-7.654683D-07
 Optimization completed.
    -- Stationary point found.
 Low frequencies ---  -13.1151    0.0004    0.0009    0.0009   15.0343   18.1624
 Low frequencies ---  371.3435  404.2381  565.2603

Population analysis

Dspace: http://hdl.handle.net/10042/22542
File:Boratabenzene NBO mb3210.log

Calculation summary
Parameters
File Type .log
Calculation Type SP
Calculation Method RB3LYP
Basis Set 6-31G(d,p)
Charge -1
Spin Singlet
Total energy(a.u.) -219.02052979
Dipole Moment(Debye) 2.85
Point Group C2V
Time taken 57.9 seconds

Borazine

Optimisation

Gaussview image of borazine

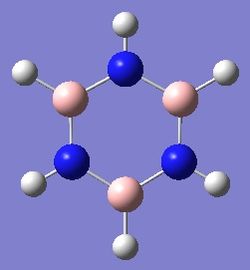
Dspace: http://hdl.handle.net/10042/22548
File:Borazine OPT 631G mb3210.log

Calculation summary
Parameters
File Type .log
Calculation Type FOPT
Calculation Method RB3LYP
Basis Set 6-31G(d,p)
Charge 0
Spin Singlet
Total energy(a.u.) -242.68458184
RMS Gradient(a.u.) 0.00006419
Dipole Moment(Debye) 0.00
Point Group D3H
Time taken 2 minutes 28.6 seconds 


Item               Value     Threshold  Converged?
 Maximum Force            0.000085     0.000450     YES
 RMS     Force            0.000033     0.000300     YES
 Maximum Displacement     0.000251     0.001800     YES
 RMS     Displacement     0.000075     0.001200     YES
 Predicted change in Energy=-9.320688D-08
 Optimization completed.
    -- Stationary point found.

Optimised B-N bond length: 1.43Å
Optimised B-H bond length: 1.19Å
Optimised N-H bond length: 1.01Å

Experimentally, the B-N bond length is 1.44Å[6] compared to the calculated length of 1.43Å (0.7% error), the B-H bond length was found to be 1.20Å[6] compared to the calculated length of 1.19Å(0.83% error) and the N-H bond length was found to be 1.02Å[6] compared to the optimised length of 1.01Å(0.99% error). These bond lengths show that literature values obtained experimentally and calculated values are in very close agreement, emphasising the accuracy of experimental techniques as well as showing that Gaussview combined with Gaussian are very powerful tools in modern chemistry.

Frequency analysis

Dspace: http://hdl.handle.net/10042/22550
File:Borazine FREQ mb3210.log

Calculation summary
Parameters
File Type .log
Calculation Type FREQ
Calculation Method RB3LYP
Basis Set 6-31G(d,p)
Charge 0
Spin Singlet
Total energy(a.u.) -242.68458184
RMS Gradient(a.u.) 0.00006436
Imaginary Freq 0
Dipole Moment(Debye) 0.00
Point Group D3H
Time taken 2 minutes 1.3 seconds 
Item               Value     Threshold  Converged?
 Maximum Force            0.000203     0.000450     YES
 RMS     Force            0.000064     0.000300     YES
 Maximum Displacement     0.000311     0.001800     YES
 RMS     Displacement     0.000098     0.001200     YES
 Predicted change in Energy=-1.075851D-07
 Optimization completed.
    -- Stationary point found.
Low frequencies ---  -12.7010  -12.4894   -9.0645   -0.0099    0.0374    0.0776
 Low frequencies ---  289.1171  289.1263  403.9186

Population analysis

Dspace: http://hdl.handle.net/10042/22551
File:Borazine NBO mb3210.log

Calculation summary
Parameters
File Type .log
Calculation Type SP
Calculation Method RB3LYP
Basis Set 6-31G(d,p)
Charge 0
Spin Singlet
Total energy(a.u.) -242.68458184
Dipole Moment(Debye) 0.00
Point Group D3H
Time taken 51.9 seconds

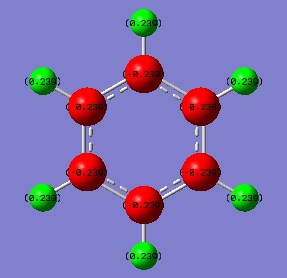
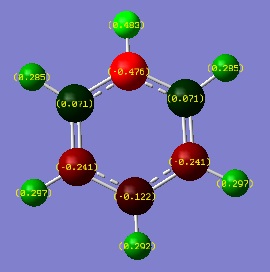
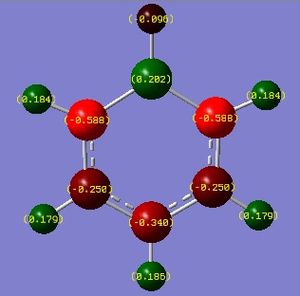
Comparing NBO analysis of benzene, pyridinium, boratabenzene and borazine

Links to Dspace for the NBO analysis can be found under "Population analysis" section of each molecule.

Comparison of NBO analysis for benzene, pyridinium, boratabenzene and borazine
Molecule Net charge NBO charge Charge range Description
Benzene 0
Gaussview image of benzene NBO charge
Gaussview image of benzene charge range
 Benzene is a fully symmetric molecule consisting of an all carbon 6 membered ring, each with one hydrogen attached. Hence, the electrons are fully delocalised so the charge distribution is even among the carbon atoms and likewise between the hydrogen atoms. The 6 carbons each have an NBO charge of -0.239 whilst the hydrogens have an NBO charge of +0;239 each. The negative sign on the charge of the carbons indicates that carbon is more electronegative than hydrogen.
Pyridinium +1
Gaussview image of pyridinium NBO charge
Gaussview image of pyridinium charge range
 Pyridinium is isoelectronic with benzene. The substitution of a C-H group in benzene for NH+ gives pyridinium. This distorts the π electron cloud and given that nitrogen is more electronegative than carbon, the nitrogen has an NBO charge of -0.476 while the carbons directly attached have an NBO charge of +0.071. This represents the inductive effect. This is in comparison to -0.239 in benzene where carbon was the most electronegative atom. It is also worth noting that the carbon atoms in the meta positions with respect to nitrogen have an NBO charge of -0.241 whereas the carbon atom in the para position has an NBO charge of -0.122. This can be explained by considering the resonance of the positive charge on the nitrogen which means the most stable resonance form is where the positive charge resides on this para carbon, hence making its NBO charge more positive than the meta carbons. The hydrogens attached to the carbon atoms have an NBO charge between 0.285 and 0.297 which is more positive than in benzene due to the electron-withdrawing effects of nitrogen. The hydrogen atom directly attached to nitrogen has the highest NBO charge in this molecule at 0.483.
Boratabenzene -1
Gaussview image of boratabenzene NBO charge
Gaussview image of boratabenzene charge range
 Boratabenzene is also isoelectronic with benzene, with BH- replacing a C-H unit. This also distorts the π electron cloud. Boron is less electronegative than carbon so the NBO charge of boron is positive at 0.202 and the carbons directly attached have an NBO charge of -0.588. The carbons at the meta position have an NBO charge of -0.250 while the carbon at the para position has an NBO charge of -0.340. Similarly, we can invoke the same argument as for pyridinum, only that in this case, it is the resonance of a negative charge and hence, the para position has a more negative NBO charge.
Borazine 0
Gaussview image of borazine NBO charge
Gaussview image of borazine charge range
 Borazine is isoelectronic and isostructural with benzene with three alternating B-H and N-H units. The NBO charges for each unit remain consistent throughout. Each nitrogen atom has an NBO charge of -1.102 and its associated hydrogen atom is 0.432. The boron atoms have an NBO charge of 0.747 each while their more electronegative hydrogens have an NBO charge of -0.077 each.

Comparison of molecular orbitals

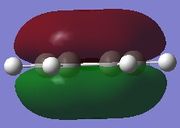
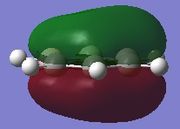
Comparison of MOs for benzene, pyridinium, boratabenzene and borazine
Molecule Fully s-bonding π1 HOMO
Benzene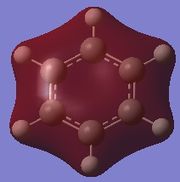
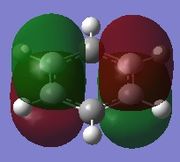
Pyridinium
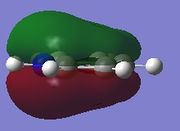Boratabenzene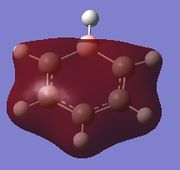
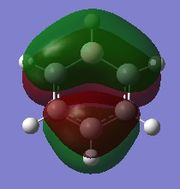Borazine

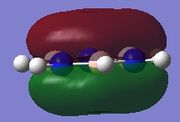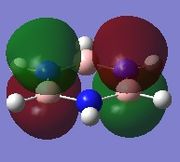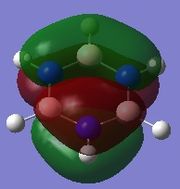
Fully s-bonding

Since this is the fully bonding s orbital molecular orbitsl there are no nodal planes present. Benzene will be used as a reference molecule. It is totally symmetric and has an even, delocalised electron distribution amongst its carbon atoms. Borazine, similar to benzene is highly symmetric, however there is a slight difference in the electron distribution due to the difference in electronegativity of nitrogen and boron (Pauling electronegativity values, N = 3.0, B = 2.0)[7][8]. It can be seen that there is reduced electron density at the boron atoms and increased electron density at the nitrogen atoms. The presence of the nitrogen atom in pyridinium distorts the electron cloud towards the nitrogen where there is greater electron density compared to the carbon atoms in the molecule. In contrast, in boratabenzene, since it is less electronegative than carbon, there is more electron density localised on the carbon atoms in the ring making the boron atom electron deficient.

π1

The π1 molecular orbital for each molecule demonstrates the concept of electron delocalisation, since there is a region of electron density delocalised above and below the plane of the molecule, with a nodal plane perpendicular to the principal axis. Hence, this illustrates that all four molecules are aromatic. On closer inspection in can be seen however, that the distribution of the electron density in both pyridinium and boratabenzene is not uniform as seen in both benzene and borazine. This is due to the difference in electronegativity between the heteroatom and the carbon atoms. In boratabenzene, the electron density appears to be deficient on the boron atom since it is electropostive with respect to carbon (Pauling electronegativity values, B = 2.0, C = 2.5[8]). Therefore, the calculated MO concurs with what we would expect to observe and the boron atom can be considered to be donating less electron density into the π1 molecular orbital compared to carbon. As a result, using benzene as a reference, boratabenzene can be considered to be less stable that benzene due to the Lewis acidity of the boron atom, which would disrupt the aromaticity of the molecule. On the other hand, in pyridinium, the difference in Pauling electronegativities in nitrogen and carbon results in more electron density being localised on the more electronegative nitrogen atom compared to the carbon atoms (Pauling electronegativity values, N = 3.0, C = 2.5[7]. Therefore, the nitrogen atom donates more electron density into the π1 molecular orbital compared to carbon. As a result pyridinium is more stable than benzene since the lone pair on nitrogen is perpendicular to the aromatic ring so doe not contributre to the aromatic system. This means that protonation of nitrogen does not disrupt the aromaticity giving a more stable molecule than benzene, which when protonated loses its aromaticity.


HOMO

By analysing the energy of the individual MOs produced in GaussView, it is apparent that both benzene and borazine have degenerate HOMOs corresponding to π2 + π3, while both pyridinium and boratabenzene have only one MO in the HOMO, π2. This can be attributed to the higher degree of symmetry found in both benzene and borazine compared to pyridinium and boratabenzene, where a carbon atom has been substituted for a heteroatom. The HOMOs across all four molecules have a nodal plane in the plane of the principal axis. For benzene and borazine, one of the MOs has 4 pz orbitals, 2 in phase on one side of the ring, 2 out of phase on the other side, while the other MO has 6 pz orbitals with 3 in phase on one side of the ring and 3 out of phase on the other side of the ring. In pyridinium, the HOMO has 4 pz orbitals, 2 in phase on one side of the ring, 2 out of phase on the other side. In boratabenzene, the HOMO contains 6 pz orbitals with 3 in phase on one side of the ring and 3 out of phase on the other side of the ring.

Comparison of MO energies between benzene, pyridinium, boratabenzene and borazine

Comparison of energies for the listed MOs for benzene, pyridinium, boratabenzene and borazine
Molecule Fully s-bonding π1 HOMO
Benzene -0.84678 -0.35999 -0.24691 (degenerate)
Pyridinium -1.21402 -0.64064 -0.47885
Boratabenzene -0.60434 -0.13208 +0.01093
Borazine -0.88851 -0.36130 -0.27590 (degenerate)

Fully s-bonding

The fully bonding s-orbitals for each molecule represents the lowest energy all bonding combination of orbitals. There are orbitals much lower in energy in each molecule, however, these consist of the 1s orbitals for a couple of the carbon atoms, and therefore do not represent a bonding combination. The energies generated help emphasise the point noted earlier which was that pyridinium is more stable than benzene, while boratabenzene is less so. The energy for pyridinium is more negative than benzene, indicating the greater stability of this MO, while for boratabenzene it is less negative. Borazine has a similar energy to benzene, highlighting their similarities in structure.

π1

Again, the same trends can be seen as noted for the fully s-bonding case. The energies for π1 are less negative than the fully s-bonding case since the overlap of p orbitals is not as great as in s orbitals, resulting in a slightly less stable molecular orbital.

HOMO

Once more, the same trends are encountered and likewise the same argument can be invoked. It is worth highlighting, however, that the HOMO for boratabenzene is positive in energy, indicating its relative instability compared to benzene's HOMOs which are negative. This further emphasises the high Lewis acidity of the boron atom in boratabenzene, which favours the formation of adducts to stablise the molecule.

Effects on the MO diagrams

Benzene and borazine will exhibit similar molecular orbital diagrams due to their high symmetry which can be seen via the presence of degenerate MOs found in found molecules. Slight differences may arise due to the differing orbital sizes and hence overlap of the orbitals, resulting in differing stabilities. For boratabenzene and pyridinium, however, we can expect more noticeable changes which will arise, due to the electronegativity difference of the heteroatoms with carbon and the loss of degeneracy associated with this. This will effect the ordering of the MOs and as a result it can be expected that boratabenzene and pyridinium will not show the same ordering.

Conclusion

This inorganic computation chemistry course has highlighted the importance and usefulness of modern computational chemistry. It has been demonstrated to be a powerful technique of which experimental data may be compared to, since a vast number of molecules known today can be optimised, frequency analysis undertaken and the computation of its molecular orbitals can be completed. As a result, our understanding of chemistry at the molecular level has improved, gaining a greater working knowledge of the reactivity of molecules and has enabled further advances in this field of chemistry. In terms of this project we have optimised a number of molecules and carried out a frequency analysis on them as well as a population analysis. We have shown the similarities of benzene and borazine in terms of their molecular orbitals and energy associated with them, as well as showing how the substitution of a carbon atom in benzene for a heteroatom can disrupt the degeneracy of the molecule.

References

  1. ↑ 1.0 1.1 J. Glaser, G. Johansson, "On the Structures of the Hydrated Thallium(III) Ion and its Bromide Complexes in Aqueous Solution", Acta Chem. Scan., 1992, 36, 125.
  2. ↑ F. Hanic, V. Šubrtová, "The Crystal Structure of Hexamethylenetetramine-Borine, C6H12N4.BH3", Acta Cryst., 1969, B25, 405.
  3. ↑ F. Allen, L. Brammer, R. Taylor, "Tables of Bond Lengths determined by X-Ray and Neutron Diffraction. Part 1. Bond Lengths in Organic Compounds", J. Chem. Soc., 1987, S5.
  4. ↑ E.F.V. Scriven, J. Toomey, R. Murugan, "Pyridine and Pyridine Derivatives", Kirk-Othmer Ency. Chem. Tech., 2000, 7
  5. ↑ 5.0 5.1 R. Islas, E. Chamorro, J. Robles, T. Heine, J.C. Santos, G. Merino, "Borazine: to be or not to be aromatic", Struct. Chem., 2007, 1-8
  6. ↑ 6.0 6.1 6.2 V.V. Volkov, K.G. Myakishev, E.A. Ilinchik, "Borazine and its derivatives: Synthesis, Mechanochemical Synthesis Reactions and Outlooks for Technological Applications", Chem. for Sustainable Development, 2009, 227
  7. ↑ 7.0 7.1 J.O McCaldin, T.C. McGill, C. A. Mead, "Correlation for III-V and II-VI Semiconductors of the Au Schottky Barrier Energy with Anion ELectronegativity", Phys. Rev. Lett., 1976, 36, 56-58
  8. ↑ 8.0 8.1 G. L. Krasko, "Effect of Boron, Carbon, Phosphorus and Sulfur on Intergranular Cohesion in Iron", Solid State Comms., 1990, 76, 247-251

Cite error: <ref> tag with name "hooke" defined in <references> is not used in prior text.

Retrieved from "https://chemwiki.ch.ic.ac.uk/index.php?title=Rep:Mod:mb3210&oldid=820150"