Rep:Mod:maw210
Computational Lab, Module 3
Maya A Wright
Computational chemistry is a useful tool in investigating key properties of a molecule such as structure, dipole moment, energy, vibrational modes, and reactivity. In this module we seek to gain insight into the transition states of two well-known chemical reactions: The Cope Rearrangement and the Diels-Alder reaction. GaussView 5.0 was used for all calculations.
The Cope Rearrangement
The Cope Rearrangement is a pericyclic reaction in which a 1,5-diene rearranges in a [3,3]-sigmatropic fashion. In this module the rearrangement of 1,5-hexadiene is studied.

To determine the mechanism of the reaction it is necessary to consider the different conformations of 1,5-hexadiene. There are six possible gauche conformations and four possible anti conformations that the 1,5-hexadiene can adopt. The energy and symmetry of each conformation was determined by optimising each molecule on GaussView 5.0.
The nature of the transition state was determined by conducting a transition state optimisation on the anti 2 conformation of 1,5-hexadiene. Different methods were employed to investigate both the chair and boat conformations. The vibrational frequency and energy of each transition state was calculated and compared.

Conformations of 1,5-hexadiene
Optimisation of 1,5-hexadiene conformers, HF/3-21G basis set
The HF/3-21G basis set was used to optimise ten possible conformations of 1,5-hexadiene. The following table summarises the energy and point groups of the possible conformations of 1,5-hexadiene.
| Conformer | Structure | Point Group | Energy (a.u.) | Relative Energy (kcal mol-1) | Optimisation File | Summary Table |
|---|---|---|---|---|---|---|
| gauche 1 | 
|
C2 | -231.68772 | 3.10 | Gauche 1 | 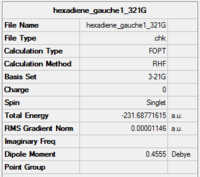
|
| gauche 2 | 
|
C2 | -231.69167 | 0.62 | Gauche 2 | 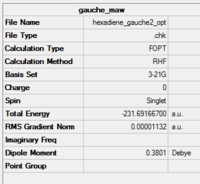
|
| gauche 3 | 
|
C1 | -231.69266 | 0.00 | Gauche 3 | 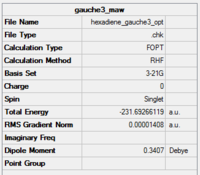
|
| gauche 4 | 
|
C2 | -231.69153 | 0.71 | Gauche 3 | 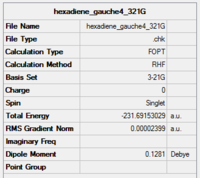
|
| gauche 5 | 
|
C1 | -231.68962 | 1.91 | Gauche 5 | 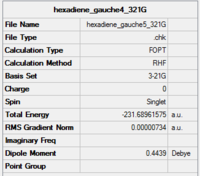
|
| gauche 6 | 
|
C1 | -231.68916 | 2.20 | Gauche 6 | 
|
| anti 1 | 
|
C2 | -231.69260 | 0.04 | Anti 1 | 
|
| anti 2 | 
|
Ci | -231.69254 | 0.08 | Anti 2 | 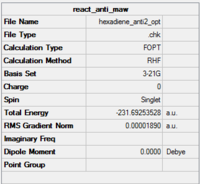
|
| anti3 | 
|
C2h | -231.68907 | 2.25 | Anti 3 | 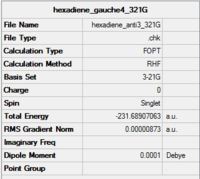
|
| anti4 | 
|
C1 | -231.69097 | 1.06 | Anti 4 | 
|
Analysis
One would expect the lowest energy conformer of 1,5-hexadiene to be one of the anti conformers, since this would have the pi bonded groups as far apart from each other as possible, thus lowering the steric repulsion. However from the above table it is apparent that the lowest energy conformer is the gauche3 molecule. This is due to favourable interactions between the pi electrons of the double bond and the nearby vinyl hydrogen atom [1].
Optimisation of 1,5-hexadiene (anti 2), 6-31G(d) basis set
The anti 2 conformer was reoptimised using a more accurate basis set (DFT, 6-31G(d)).
The optimisation file is liked to here
 |
 |
|---|
Comparison of HF/3-21G and 6-31G(d) optimised anti 2 conformer
The bond lengths do not change significantly with the basis set used, although the 6-31G(d) bond lengths are slightly shorter overall than the 3-21G bond lengths. The maximum change in bond length was about 1.4%. The 6-31G(d) calculations yielded larger bond angles than the 3-21G calculations. The C1-C2-C3-C4 dihedral angle increased by 3.4% in going from 3-21G to 6-31G(d). These changes in bond length and bond angle are negligible, so the geometry has not changed significantly in going from the 3-21G to 6-31G(d) basis set.
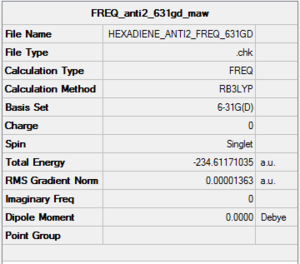
Frequency Analysis of anti2 1,5-hexadiene (6-31G(d))
A frequency analysis was conducted on the B3LYP/6-31G(d) optimised anti 2 conformer. All vibrational frequencies are real and positive, thus the obtained structure is a minimum.
The optimisation file is liked to here
 |
 |
 |
|---|
 |
 |
 |
|---|
Thermochemistry
The energy of the molecule is dependent on parameters such as the enthalpy, entropy, free energy and temperature. The following table summarises this:
Zero-point correction= 0.142507 (Hartree/Particle)
Thermal correction to Energy= 0.149853
Thermal correction to Enthalpy= 0.150797
Thermal correction to Gibbs Free Energy= 0.110933
(1) Sum of electronic and zero-point Energies= -234.469204
(2) Sum of electronic and thermal Energies= -234.461857
(3) Sum of electronic and thermal Enthalpies= -234.460913
(4) Sum of electronic and thermal Free Energies= -234.500777
(1) corresponds to the energy of the molecule at 0 K, which includes the zero-point energy. (2) is the energy of the molecule at 298.15K. This takes into account the translational, rotational, and vibrational energies. (3) corrects for the thermal energy available at room temperature, E= H + RT. (4) accounts for the entropic contribution from the free energy[2], G = H - TS
Frequency analysis of anti2 1,5-hexadiene (HF/3-21G)
A frequency calculation was done for the anti 2 conformer using the 3-21G basis set in order to obtain thermochemical information. (Later used to calculate the activation energy of the cope rearrangement via the chair and boat transition states).
The optimisation file is linked to here
Zero-point correction= 0.152996 (Hartree/Particle) Thermal correction to Energy= 0.159970 Thermal correction to Enthalpy= 0.160914 Thermal correction to Gibbs Free Energy= 0.121620 Sum of electronic and zero-point Energies= -231.539539 Sum of electronic and thermal Energies= -231.532565 Sum of electronic and thermal Enthalpies= -231.531621 Sum of electronic and thermal Free Energies= -231.570916
Chair Transition State
Three different computational methods were used to determine the structure and imaginary vibrational frequency of the chair transition state: (a) The Berny TS Optimisation (b) The Frozen Coordinates Method, and (c) The IRC Method.
Optimisation of a transition state can be difficult. The input structure must be relatively close to the true transition state structure, which corresponds to a saddle point on the potential energy surface [3]. If the starting structure is too far off, the calculation may not follow the direction of the reaction coordinate.
The Berny TS Optimisation method allows for the calculation of a local energy minimum on the potential energy surface. This is done by computing the Hessian matrix, i.e. the second derivative force matrix, at every point on the reaction coordinate[4]. Since an exact calculation of the Hessian matrix takes too long, GaussView uses approximate Hessian matrices instead. For this to work the starting structure must resemble the true structure.
In the Frozen Coordinates method the distance between the terminal carbon atoms is fixed while the rest of the molecule is optimised. Unlike the Berny TS method, after the molecule has been optimised it is not necessary to calculate the Hessian for every point. Instead, the terminal carbon distance is unfrozen and the derivative is taken along the reaction coordinate until it reaches a minimum.
The IRC (or Intrinsic Reaction Coordinate) method allows for us to follow the minimum energy pathway of a reaction. This requires the initial force constants[5], so the calculation is based on the Berny optimised TS structure. The calculation proceeds in the direction with the steepest slope on the potential energy surface.
Optimisation of an allyl fragment (HF/3-21G)
As a first step to computing the transition structure, an allyl fragment was optimised. The optimisation file is liked to here
 |
 |
|---|
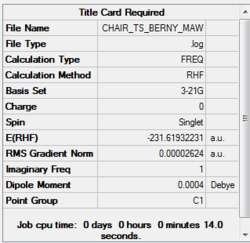
Berny Optimisation of the chair transition state (HF/3-21G)
The HF/3-21G optimised allyl fragment was used to construct a 'guess' chair transition state structure. The guess structure was arranged with the terminal carbon atoms approximately 2.2 Å apart. The Job Type was set to Opt+Freq/ Optimise to a TS (Berny). The force constants were calculated 'Once' and the words 'Opt=NoEigen' were added to the additional keywords box in order to stop the calculation from crashing in case more than one imaginary frequency was computed.
The optimisation file is liked to here
 |
 |
|---|
The imaginary frequency occurs at 818 cm-1. This clearly resembles the Cope rearrangement as the terminal C atoms oscillate toward and then away from each other. One can imagine a bond forming between the terminal C atoms as they approach each other, and then breaking as they move away from each other.
Bond forming/ breaking length: 2.02 Å
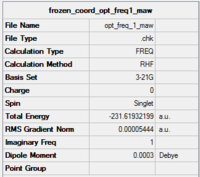
Optimisation of chair transition state: Frozen Coordinates Method (HF/3-21G)
The chair transition state was optimised using the frozen coordinates method. First, the terminal C-C bond lengths were frozen to 2.2 Å while the rest of the molecule was optimised using the HF/3-21G basis set (Keywords: Opt=modredundant). Then the terminal bond lengths were unfrozen and the derivative was taken along the path with the steepest slope on the potential energy surface. The results of the second calculation are given below:
The optimisation file is linked to here
 |
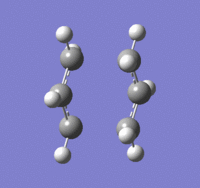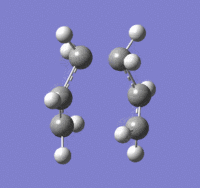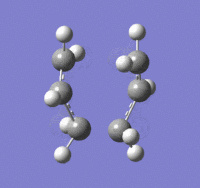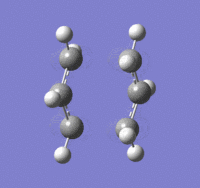 |
|---|
The imaginary frequency occurs at 818 cm-1 which is in agreement with the Berny TS optimisation method.
Bond forming/ breaking length: 2.02 Å
The bond forming/ bond breaking bond length is the same as that calculated by the Berny TS optimisation. It is smaller than the initial guess of 2.2 Å. The energies for the Berny TS and Frozen Coordinates optimised molecules are also the same at -231.619322 a.u. The fact that the vibrational frequency, bond forming/ bond breaking length, and the energies of the two molecule are in good agreement shows that the two strucutres are very similar.
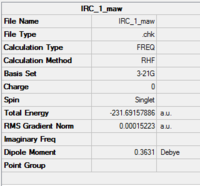
Optimisation of chair transition state: IRC Method (HF/3-21G)
The minimum energy pathway of the reaction was followed using the Intrinsic Reaction Coordinate method. The previously optimised berny transition state structure was used for the input file. 50 iterations were taken and the reaction coordinate was computed only in the forward direction.
The optimisation file is linked to here
 |
 |
|---|
 |
 |
|---|

 |
 |
|---|
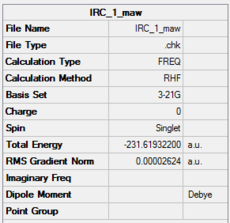
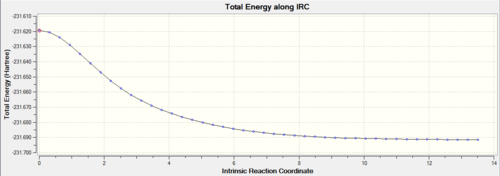
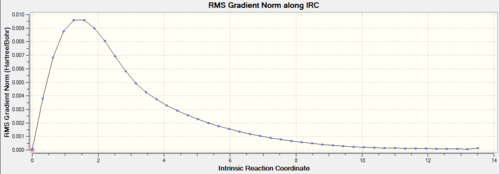
Graph (1) maps the energy of the molecule as a function of optimisation step number. As the optimisation progresses, the energy of the molecules approaches a constant value. This shows that the calculation is approaching a minimum geometry. However on inspection of graph (2) it is apparent that the RMS gradient has not quite reached zero in the last step. Thus a further optimisation must be carried out.
Second optimisation
A further optimisation was carried out on the last IRC structure (no. 44) in order to ensure that an energy minimum was reached. The 44th structure was optimised to a minimum.
The optimisation file is linked to here
 |
|
|---|
Optimisation of chair transition state using 6-31G(d) basis set
The Berny optimised chair transition state (HF/3-21G) was reoptimised using a higher accuracy 6-31G(d) basis set. A frequency analysis was also conducted.
The optimisation file is linked to here
 |
 |
|---|
Boat Transition State
Optimisation of boat transition state- QST2
The boat TS was optimised using the QST2 method. This method requires the input of a reactant and product structure so that the calculation can flit between the two structures in order to find the transition state. The reactant and product molecules were arranged so that their geometries resembled that of the boat transition state. The C2-C3-C4-C5 dihedral angle was set to 0° and the C2-C3-C4 and C3-C4-C5 inner angles were set to 100°. The reactant and product molecules were numbered so that their connectivity resembled that of the cope rearrangement.
 |
 |
|---|
The optimisation file is linked to here
Vibrational Frequency
The optimised boat structure has one imaginary frequency at -840 cm-1

Optimisation of boat transition state using 6-31G(d) basis set
The HF/3-21G optimised boat transition state was reoptimised using a higher accuracy 6-31G(d) basis set.
The optimisation file is linked to here
 |
 |
|---|
Comparison of 3-21G and 6-31G(d) optimised reactant and transition state structures
By visual inspection of the optimised reactant/ transition state molecules in the above sections, the geometries of the molecules do not change significantly with the basis set used. However, there is a notable difference in energy between the two levels of theory, with the 6-31G(d) basis set predicting the existance of lower energy reactants and transition states. The energies of the reactants and transition states for each level of theory is compared in the table below.
| HF/3-21G | B3LYP/6-31G(d) | |||||
|---|---|---|---|---|---|---|
| Electronic energy | Sum of electronic and zero-point energies (0 K) | Sum of electronic and thermal energies (298.15 K) | Electronic energy | Sum of electronic and zero-point energies (0 K) | Sum of electronic and thermal energies (298.15 K) | |
| Chair TS | -231.619322 | -231.466706 | -231.461345 | -234.556983 | -234.414929 | -234.409008 |
| Boat TS | -231.602802 | -231.450930 | -231.445302 | -234.543093 | -234.402339 | -234.396006 |
| Reactant (anti2) | -231.692535 | -231.539539 | -231.532565 | -234.611710 | -234.469204 | -234.461857 |
The activation energy for the Cope Rearrangement was calculated by taking the difference between the transition state and reactant molecule energies at 0 K and 298.15 K. These values are compared to experimentally determined activation energies.
| HF/3-21G | B3LYP/6-31G(d) | Experimental[6] | |||
|---|---|---|---|---|---|
| 0 K | 298.15 K | 0 K | 298.15 K | 0 K | |
| ΔEa Chair | 45.70 | 44.69 | 34.06 | 33.16 | 33.5 ± 0.5 |
| ΔEa Boat | 55.60 | 54.76 | 41.96 | 41.32 | 44.7 ± 2.0 |
The calculated activation energies at 0 K for the higher accuracy basis set (6-31G(d)) gives a closer match to the experimental data for both the chair and boat conformations. Also, the chair transition state is predicted to have a lower activation energy than the boat transition state. Thus, one may be led to think that the reaction proceeds via the chair transition state. However, there is still much controversy on whether this is true. One definite conclusion is that the computed transition state vibrations show the reaction occurring in a concerted fashion. The dotted lines show that the electrons involved in the reaction are delocalised and that they are not fixed between any two atoms. Thus it is likely that the mechanism for the cope rearrangement is concerted and goes via either a chair or boat transition state.
The Diels-Alder Reaction
The Diels-Alder reaction is a pericyclic reaction in which a diene reacts with an alkene (dienophile) in a concerted fashion. The reaction is successful because of the matching orbital symmetry of the diene HOMO/dienophile LUMO and vice versa. The p orbitals of each reactant overlap head on to form two new σ bonds via a stable, aromatic transition state.

In the first section we compute the HOMO and LUMO of butadiene in order to gain insight into the frontier orbitals that are key to the Diels-Alder reaction. We then go on to investigate the reaction of ethylene and butadiene.

The transition state of the reaction is computed and its mechanism is discussed.
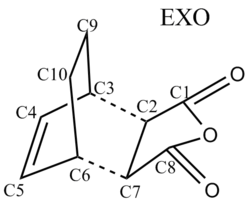
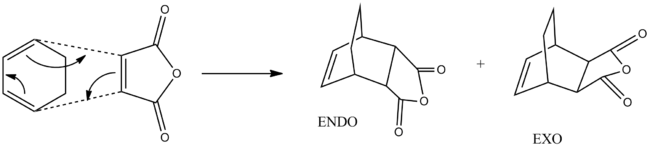
Finally, we explore the Diels-Alder reaction between Cyclohexa-1,3-diene and maleic anhydride in which there are two possible products: a kinetically stable endo product and a thermodynamically stable exo product.
Note: Solvent effects are ignored.
Butadiene
AM1 semi-emperical optimisation of cis-butadiene
The geometry of cis-butadiene was optimised using the AM1 semi-empirical method.
The optimisation file is linked to here
 |
 |
|---|
 |
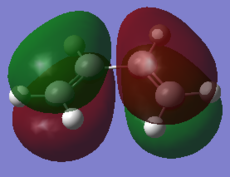 |
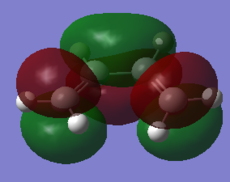 |
|---|
Ethylene + Butadiene
Berny optimisation of the transition state
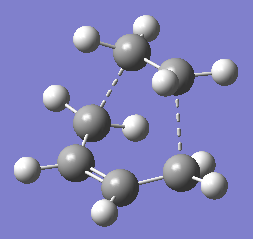
The transition state of the reaction of ethylene with butadiene was optimised using the AM1 semi-empirical/ Berny TS method. The interfragment distance between ethylene and butadiene was set to be 2.2 Å in the optimisation, as quoted in literature [8].
The optimisation file is linked to here
 |
 |
|---|---|
 |
 |
The optimised structure clearly corresponds to the Diels-Alder transition state. There is only one imaginary frequency in the optimisation, and one can visualise bonds forming as the ethylene/ butadiene move toward each other in the vibration and breaking as they move away from each other. The bond forming/ breaking process is synchronous and concerted. The dotted lines indicate that the electrons are delocalised and that the σ bonds have not yet completely formed, a characteristic trait of a transition state. The lowest positive frequency at 147 cm-1 does not show the carbon atoms on ethylene/ butadiene getting closer to each other. The ethylene carbon atoms rock from side to side in the plane of the molecule and so do the butadiene carbon atoms. Since the two reactants do not move toward or away from each other in this positive vibrational mode, it does not correspond to the transition state.
| sp3 C-C | sp2 C=C | sp3-sp2 C-C | van der Waals radius of C | partly formed σ C-C bond |
| 1.52 | 1.33 | 1.50 | 1.70 | 2.12 |
As the ethylene and butadiene move towards each other in the imaginary vibration, the carbon atoms joined by the dotted lines change from sp2 to sp3 character. However when stationary the partly formed σ C-C bond length is 2.12 Å. This is closer to the sp3 - sp3 C-C bond length (1.52 Å) so the transition state must resemble the products more than the reactants, i.e. the reaction has a late transition state. The partly formed σ C-C bond can also be visualised as two individual C atoms of van der Waals radii 1.70 Å starting to meet within the attractive range of each other so that eventually a bond can be formed between them.
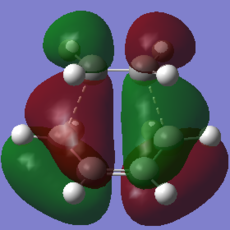 |
 |
|---|
The HOMO of the transition structure is antisymmetric with respect to the plane. In this case it is the HOMO of butadiene that reacts with the LUMO of ethylene to form the frontier orbitals of the transition state. The formation of the TS HOMO can be visualised using the following MO diagram:
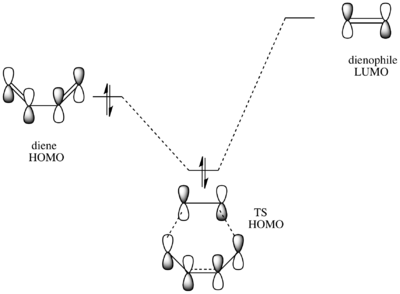
The electron rich double bonds of butadiene donate into the electron deficient ethylene LUMO. The reaction is allowed because of the symmetry of the interacting orbitals. Both the HOMO of butadiene and the LUMO of ethylene are a (antisymmetric) with respect to the plain of symmetry. Thus the HOMO of the product that they form is also a because reactions in which the reactants and products have the same electron distribution are favoured [10].
Kinetic vs Thermodynamic Control
Dienes and dienophiles that are appropriately substituted can form stereochemical products. This phenomenon arises because there are two ways in which the dieneophile can approach the diene: facing toward (endo) or away (exo) from the diene. The endo product is the kinetically favoured product as it is formed faster, whereas the exo product is thermodynamically more favoured as it is lower in energy. In this module we investigate the reaction of cyclohexa-1,3-diene with maleic anhydride.
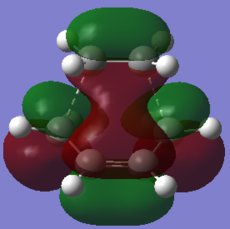
Endo Product
The endo transition state for the reaction of Cyclohexa-1,3-diene and maleic anhydride was optimised using the AM1 semi-empirical/ frozen coordinates method. The terminal C-C bond lengths were set to 2.1 Å.
The optimisation file could not be uploaded because it exceeded 2.0 MB.
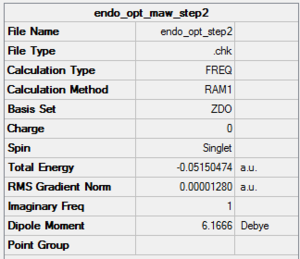 |
 |
|---|
The imaginary frequency occurs at -806 cm-1
Exo Product
The exo transition state for the reaction of Cyclohexa-1,3-diene and maleic anhydride was optimised using the AM1 semi-empirical/ frozen coordinates method. The terminal C-C bond lengths were set to 2.1 Å.
The optimisation file is linked to here
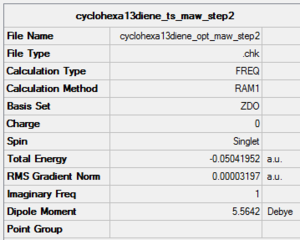 |
 |
|---|
The imaginary frequency occurs at -812 cm-1
Comparison of Endo and Exo
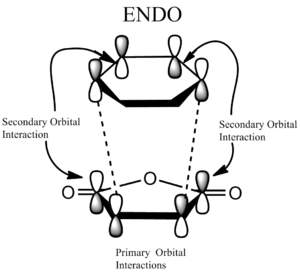
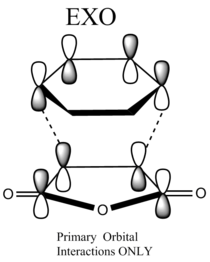
The following diagram shows the overlap of the reactant molecules and how they react to form the endo/ exo product. In both cases the electron rich cyclohexa-1,3-diene HOMO donates electrons into the electron deficient maleic anhydride LUMO.
 |
 |
|---|
The Endo TS has two sets of favourable interactions: the primary and secondary orbital overlaps. Because the maleic anhydride reacts with its O atom facing toward the diene, additional non-bonding π-interactions can occur between the p orbitals on the carbonyl carbons and that of the carbon atoms forming the new double bond. As a result the energy of the endo TS is lowered and the endo product forms faster. This is consistent with the obtained calculations: The energy of the endo TS is -32.3 kcal mol-1 and the energy of the exo TS is -31.6 kcal mol-1. The energies are very close, but the endo TS has a slightly lower energy than the exo TS, hence the endo structure is kinetically favoured.
The HOMO of the endo and exo transition states are shown below. As expected, the endo HOMO is lower in energy than the exo HOMO. Both HOMOs are antisymmetric with respect to the plane. It is interesting to see that there is an absence of MO lobes around the -(C=O)-O-(C=O)- fragment. This is not the expected outcome of the secondary orbital overlap effect, since the SOO predicts that bonding interactions exist between the -(C=O)-O-(C=O)- fragment and the newly forming double bond. This suggests that either (a) the computational methods used to visualise these orbitals are not accurate enough, or that (b) the secondary orbital overlap is a useful way of rationalising the favoured formation of the endo product, but its validity is questionable.
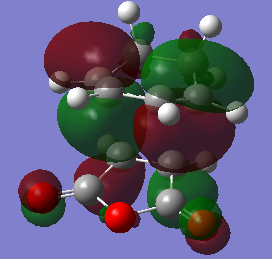 |
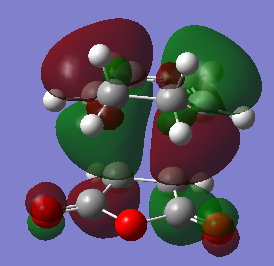 |
|---|
The table below summarises key C-C bond lengths in the endo and exo transition states. This includes directly bonded carbons and through space interactions of carbons.
The partly formed σ C-C bonds have nearly the same distance in both endo and exo structures. In both structures the C3-C4 and C5-C6 bond lenghts are slightly longer than that of a typical C=C double bond (1.33 Å), indicating that the C3-C4 and C5-C6 bonds are reacting to form single bonded carbons. The C4-C5 bond is shorter than that of a typical C-C single bond (1.52 Å), which indicates that a double bond is forming.
The C1-C4/ C8-C5 through space distance in the endo product is shorter than the C1-C9/ C8-C10 interaction in the exo product. The shorter distance (i.e. larger strain) in the endo product is a trade off for the favourable secondary orbital overlap interactions observed in the transition state.
References
- ↑ Brandon C. et. al., MOLECULAR PHYSICS, 2002, 100, 4, 441-446
- ↑ Module 3 Laboratory Script
- ↑ Lewars, E., Computational Chemistry, Springer, London, p.17
- ↑ http://www.chem.cornell.edu/dbc6/documents/Gaussian_optimization.pdf
- ↑ http://www.gaussian.com/g_tech/g_ur/k_irc.htm
- ↑ Module 3 Laboratory Script
- ↑ Module 3 Laboratory Script
- ↑ Goldstein E.,J. Am. Chem. Soc., Vol. 118, No. 25, 1996-6039
- ↑ Margules, L. Structural Chemistry, Vol. 11, Nos. 2-3, 145- 154
- ↑ http://www.ch.ic.ac.uk/local/organic/pericyclic/