Rep:Mod:matthew adams
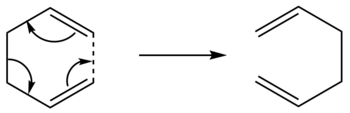
Cope Rearrangement
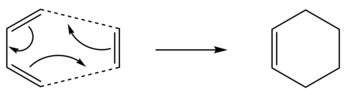
The Cope rearrangement involves a [3,3]-sigmatropic shift rearrangement of 1,5-hexadiene. The mechanism is usually recognized as a concerted process via either a 'chair' or a 'boat' transition structure. The preferred configuration of reactants, products and transition states will be optimised to give an accurate reaction mechanism. The reaction scheme is below:
Optimising Reactants
Firstly a molecule of 1,5-hexadiene with an anti peri-planar conformation for the central carbon atoms was made in GaussView and the structure cleaned. This was then optimised using the Hartree Fock method and 3-21G basis set. The optimised structure is shown in Figure 1. The total energy of the structure was -231.69260220 a.u. and has C2 symmetry.
Figure 1. 1,5-Hexadiene Anti 1 |
A second anti peri-planar structure was made and optimised in the same way as the structure but it had Ci symmetry. This structure is shown in Figure 2 and has a total energy of -231.69253516 a.u.
Figure 2. 1,5-Hexadiene Anti 2 |
A gauche structure was made and optimised using Hartree Fock and the 3-21G basis set. This has a total energy of -231.68771610 a.u. and C2 symmetry. The structure is shown in figure 3.
Figure 3. 1,5-Hexadiene Gauche |
The lowest energy conformer was found to be the gauche which was not expected (Your gauche conformer is actually higher in energy than either of your anti structures João (talk) 17:20, 22 December 2014 (UTC)). The anti peri-planer structure would have been expected to be lower in energy due to the R groups being 180° apart when looking at a newman projection. The gauche only has the R groups 60° apart. The reason for the lower energy could be due to the orbital overlap of the 2 double bonds which would have stabilise the gauche conformer. This comparison is shown in Figure 4 and 5.
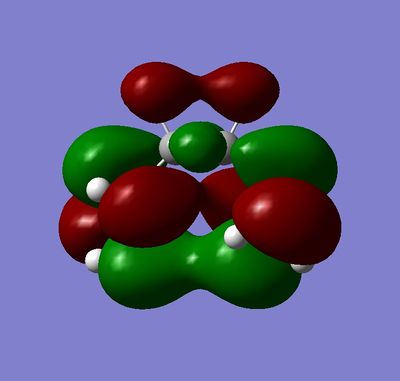 |
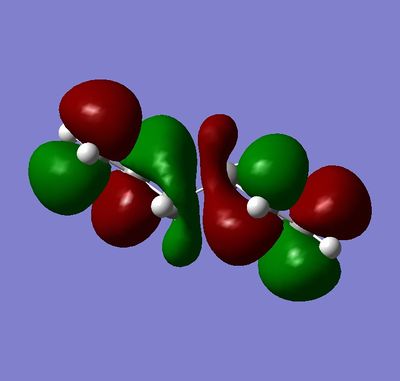 |
The Ci anti conformer shown in Figure 2 was then optimised again using density functional theory - Becke three-parameter Lee-Yang-Parr exchange-correlation functional and the 6-31G* basis set. The structure is shown in Figure 6. The total energy was found to be -234.61171062 a.u. and maintained the Ci symmetry. Frequency analysis shows all positive values (from 73.42cm-1 to 3232.77cm-1), therefore confirms the optimisation is correct. (It confirms that you calculated a minimum structure at the chosen level of theory.</span João (talk) 17:20, 22 December 2014 (UTC))
Figure 6. 1,5-Hexadiene Anti2 - B3LYP |
| Geometry parameters | HF/3-21G | B3LYP/6-21G* | Literature Value[1] |
|---|---|---|---|
| C4-C1-C14-C6 dihedral |
180.0° | 180° | 179.3° |
| C11-C4-C1 bond angle |
124.8° | 125.3° | 122.5° |
| C11-C4 bond length |
1.316Å | 1.333Å | 1.341Å |
| C4-C1 bond length |
1.509Å | 1.504Å | 1.508 Å |
| C1-C14 bond length |
1.553Å | 1.548Å | 1.536 Å |
As the literature value is based on experimental data so includes measurement of an average of anti peri-planar conformers. The B3LYP/6-31G* is generally closer to literature although at points HF/3-21G is closer but on the whole it is more erratic so can't be considered as accurate as the B3LYP/6-31G* method. (The important point is that the structures calculated at different levels of theory are very similar. João (talk) 17:20, 22 December 2014 (UTC))
The predicted IR spectra for the optimised anti 2 structure is below and compared with an experimental one
 |
 |
This shows that the computational IR matches well with the experimental[2] (What criteria did you use to make your assessment? Nice thing that you attempted to compared with experiment though. João (talk) 17:20, 22 December 2014 (UTC))
Optimising the "Chair" and "Boat" Transition Structures
Both the "Chair" and "Boat" transition structures can be made from the combination of two identical allyl (C3H5) fragments. It is therefore very important to optimise the fragment before attempting to calculate the transition structures as it reduces the chance of errors occurring.
Allyl fragment
The fragment was optimised using Hartree Fock and 3-21G basis set. It was found to have a total energy of -115.82 a.u. and the structure is shown in Figure 7.

"Chair" Transition Structure
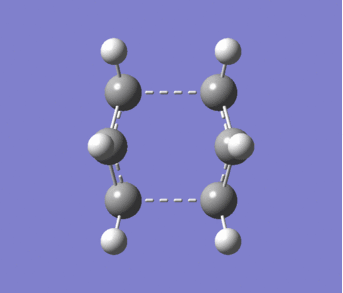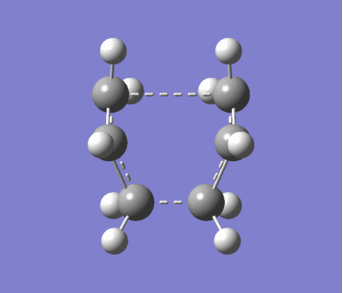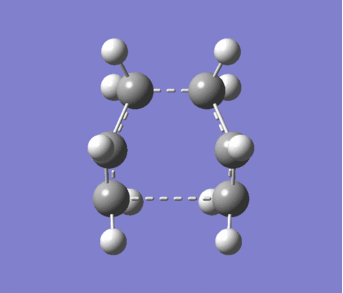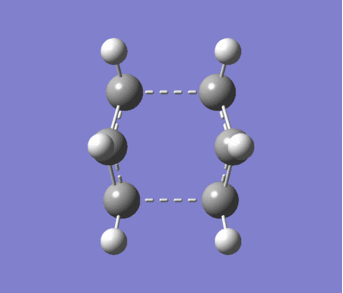
The "Chair" structure was created by positioning two of the allyl fragments with the terminal carbons approximately 2.2Å apart and the central carbons pointing in opposite directions. An optimisation and frequency calculation was then run using the Hartree Fock method and 3-21G basis set. Although unlike earlier calculations this was calculated to a TS (berny) and not to a minimum. The optimised structure can be seen in Figure 8. The frequency calculation gave an imaginary vibration (-817.91cm-1) which can be seen in Figure 9 and corresponds to the cope rearrangement.
 |
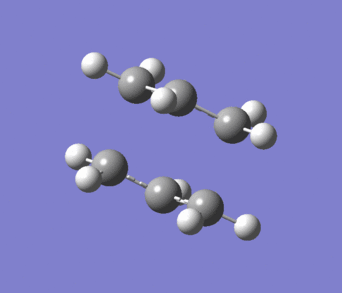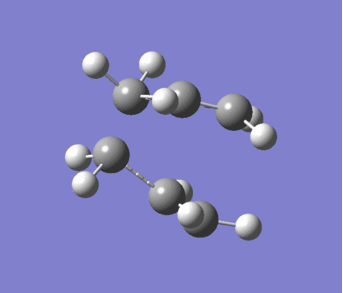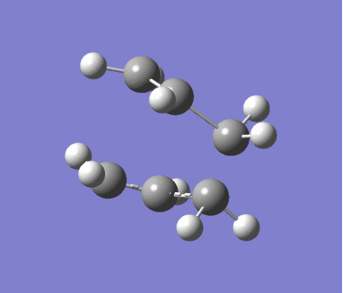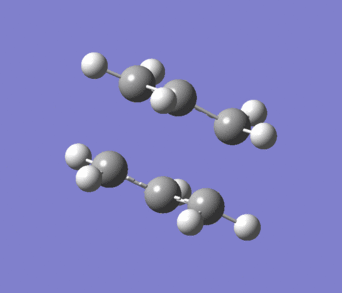 |
The calculation was then carried out in the same way but with fixed lengths between the terminal carbons of 2.2Å. This gave a frequency of -764.92cm-1 which is quite different to the original value that was obtained (This is an intermediate step on the calculation of the transition state. The frozen coordinate structure has little meaning by itself. João (talk) 17:20, 22 December 2014 (UTC)). The caculation was then carried out but with the bonds allowed to derivate from 2.2Å this gave a frequency of -817.81cm-1 which seems the most realistic result. (More realistic why? João (talk) 17:20, 22 December 2014 (UTC))
"Boat" Transition Structure
The "Boat" structure was found by using the quadratic synchronous transit 2 method. This required the previously B3LYP/6-31G optimised 1,5-hexadiene to be added twice to a Molecule group in GaussView and then the atom numbers of one of the structures was changed to thew product of the cope rearrangement. The resulting "Boat" transition structure is shown in figure 10. An imaginary vibration (-504.21cm-1) which is shown in figure 11 and corresponds to the cope rearrangement.
 |
 |
Thermochemistry
The thermochemistry data for the B3LYP/6-31G* optimised boat and Chair is presented in the table below:
| Geometry parameters | Boat TS | Chair TS |
|---|---|---|
| Sum of electronic and zero-point energies at 0K | -234.402632 a.u. | -234.412682 a.u. |
| Sum of electronic and zero-point energies at 298.15K | -234.402542 a.u. | -234.41507 a.u. |
| Sum of electronic and thermal energies at 0K | -234.396010 a.u. | -234.405147 a.u. |
| Sum of electronic and thermal energies at 298.15K | -234.396010 a.u. | -234.409002 a.u. |
(Do you expect the electronic + zero point energy to be different at 0K and 298.15K? Do you expect the electronic + thermal energy do be the same at 0K and 298.15K? João (talk) 17:20, 22 December 2014 (UTC))
(What are the activation energies? How do they differ at different levels of theory? Are the transition state structures different at different levels of theory? How do the activation energy values compare with experiment? João (talk) 17:20, 22 December 2014 (UTC))
Diels Alder Cycloaddition
The Diels Alder cycloaddition reaction is a pericyclic reaction ([4+2] cycloaddition) between a dienophile and diene. As it is a pericyclic reaction it occurs in one concerted step with only one transition structure. This makes it ideal to use computational analysis. The calculations for this part will be carried out using the AM1 semi-empirical molecular orbital method instead of the Hartree Fock and DFT previously. This method is more effective and performs better at locating transition states.
Two Diels Alder will be looked at; ethylene and cis-butatdiens, and cyclohexa-1,3-dien and maleic anhydride.
Reaction of Ethylene and Cis-Butadiene
The reaction scheme for ethylene and cis-butadiene is shown below:
Reactants
A molecule of cis-butadiene was drawn in GaussView before being cleaned and optimised to a minimum using the AM1 semi-empirical MO method. The structure is shown in figure 12. The HOMO and LUMO of the structure are shown in figure 13 and 14. (Why didn't you obtain a planar structure? Is that what you expected? João (talk) 17:20, 22 December 2014 (UTC))
Figure 12. Cis-Buradiene structure |
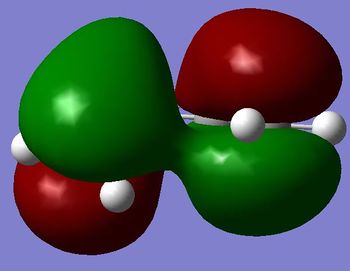 |
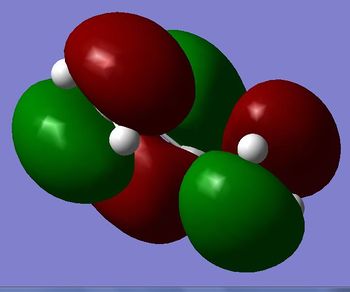 |
The HOMO is Antisymmetric to the σV plane whereas the LUMO is symmetric. (Do actually have a plane of symmetry? João (talk) 17:20, 22 December 2014 (UTC))
Ethylene was created in GaussView and cleaned before being optimised using the AM1 semi-empirical MO method. The structure is shown in Figure 15.
Figure 15. Ethylene structure |
Transition Structure
As suggested in literature[3] the transition structure was created from a biclyclo system with a CH2-CH2 unit removed and the ethylene put in its place with a distance of 2.2Å separating the molecules. This was then optimised to TS(Berny) using the AM1 semi-empirical MO method. This gave the structure in figure 16 and a vibration of -1142.28cm-1 and is shown in figure 17.
(You reactant in the figures bellow does not seem to be butadiene. João (talk) 17:20, 22 December 2014 (UTC))
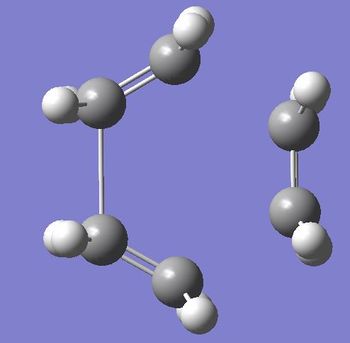 |
 |
 |
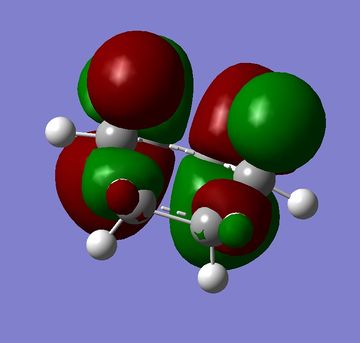 |
(Figures 16 and 17, and 18 and 19 don't seem to correspond to the same strcutures João (talk) 17:20, 22 December 2014 (UTC))
The HOMO is symmetric and the LUMO is antisymmetric relative to the plane. (What orbitals from the reactants do you "combine" to form these orbitals? João (talk) 17:20, 22 December 2014 (UTC))
Figure 20 shows the first positive vibration which helps indicate that the sigma bonds are formed synchronously. (Why does a real frequency mode show that? João (talk) 17:20, 22 December 2014 (UTC))
Reaction of Maleic Anhydride and Cyclohexa-1,3-diene
Cyclohexa-1,3-diene undergoes a cycloaddition with malice anhydride. The end product is the major and kinetic product in this reaction so it is assumed that the exo transition state must be higher in energy. In real world conditions the reaction can produce the cycloaddition product of two cyclohexa-1,3-diene molecules, this will be ignored for the purpose of these calculations. The mechanism is shown below:
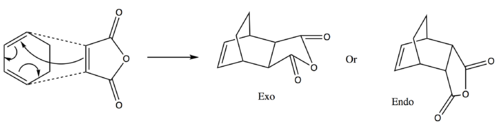 |
Reactants
To start with maleic anhydride and cyclohexa-1,3-diene were made in GaussView and cleaned. They were then both optimised to a minimum using HF/3-21G. These structures are shown in figure 21 and 22.
Figure 21. Maleic anhydride structure |
Figure 22. Cyclohexa-1,3-diene structure |
The HOMO and LUMO for maleic anhydride and cyclohexa-1,3-diene are plotted in figures 23 to 26.
 |
 |
 |
 |
The HOMO for maleic anhydride is symmetric and the LUMO is antisymmetric. The HOMO and LUMO for cyclohexa-1,3-diene are more complex and difficult to determine the symmetry.
Transition Structure
The two transition structures (exo and endo) were then both created from the optimised reactants with approximately 2.2Å between the molecules. They were then optimised to a transition structure using the QST2 method to given the structures in figures 27 and 28. The energy of the exo transition state is -605.60359124 a.u. which is higher than the energy for the endo transition structure which is -605.61036823 a.u.
 |
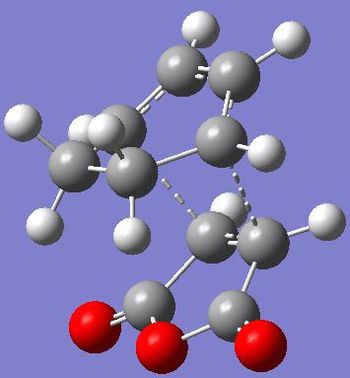 |
The bond lengths for each are on figure 29 and 30. This shows that the endo structure is the kinetic product and as such should be the preferred product. The distance between the -(C=O)-O-(C=O)- and the -CH2CH2- in the exo structure is 2.916Å. This is longer than the distance between the -(C=O)-O-(C=O)- and -CH=CH- of 2.848Å in the endo structure. This would indicate some steric hinderance in the exo structure and relates to the increased energy. All the bond lengths agree with the expected range of lengths, although the double bond in maleic anhydride has taken on single bond character lengthening to 1.370Å and 1.373Å, this has also happened with the double bonds in cyclohexadiene which have lengthened to 1.371Å and 1.370Å.
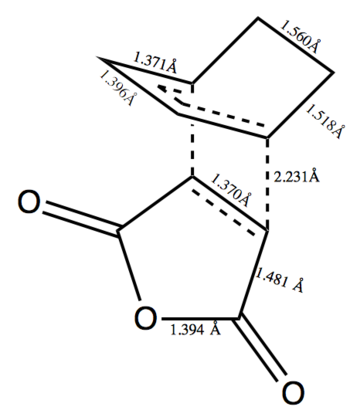 |
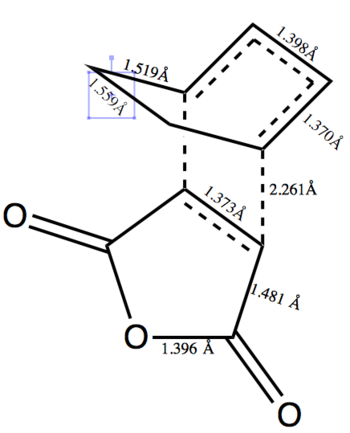 |
The vibration for each structure are -643.61cm-1 for the endo and -647.64cm-1 for the exo structure. These are shown in figure 31 and 32. The movements correspond to concerted bond formation as would be expected for the Diels Alder reaction.
 |
 |
The HOMOs and LUMOs of both the exo and endo structures are shown in figures 33 to 36. One of the main reasons for Diels Alder reaction preferences normally given is secondary orbital overlap[4] however in the HOMOs below there is no secondary orbital overlap for either the endo or exo structure so it can not be a factor in this reaction. The calculations for this reaction would indicate that sterics were the only influencing factor. This would agree with more recent literature which has questioned whether these secondary orbital overlaps exist or whether there is another reason for endo selectivity [5].
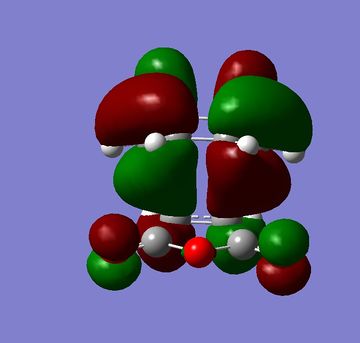 |
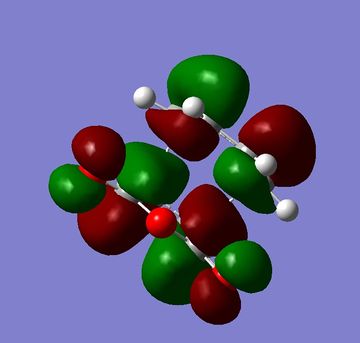 |
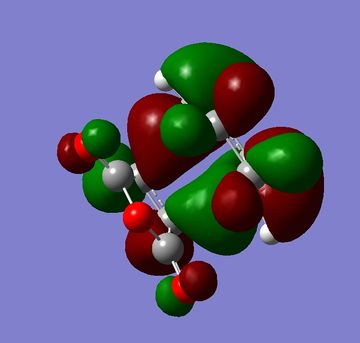 |
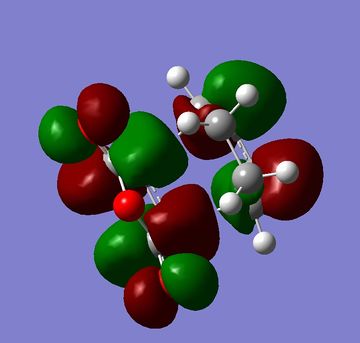 |
References
- ↑ I. H. Gyorgy Schultz, Journal of Molecular Structure, 1995, 346, 63-69.DOI:10.1016/S0022-2860(96)09454-9
- ↑ V. E. Bondybey, J. W. Nibler, Spectrochimica Acta Part A: Molecular Spectroscopy, 1973, 29, 645-658.DOI:10.1016/0584-8539(73)80094-7
- ↑ I. D. Suarez, T.L. Sordo, J.A. Sordo, J. Org. Chem., 1995, 60, 2848-2852.DOI:10.1021/jo00114a039
- ↑ I. R. Hoffmann, R. B. Woodward, J. Am. Them. Soc., 1965, 19, 4388-4389.DOI:10.1021/ja00947a033
- ↑ H. V. Pham, R. S. Paton, A. G. Ross et al., J. Am. Them. Soc., 2014, 6, 2397-2403.DOI:10.1021/ja410220w
