Rep:Mod:markwiki123
Nh3 Molecule
Key information:
Calculation method: RB3LYP
Basis set: 6-31G(d.p)
Final energy: -56.55776842 a.u.
RMS gradient: 0.00018454 a.u.
Point group: C1
N-H Bond distance: 1.01831 Angstroms
H-N-H Bond angle: 105.772 Degrees
Item Value Threshold Converged?
Maximum Force 0.000004 0.000450 YES
RMS Force 0.000004 0.000300 YES
Maximum Displacement 0.000072 0.001800 YES
RMS Displacement 0.000035 0.001200 YES
Predicted change in Energy=-5.986291D-10
Optimization completed.
----------------------------
! Optimized Parameters !
! (Angstroms and Degrees) !
-------------------------- --------------------------
! Name Definition Value Derivative Info. !
--------------------------------------------------------------------------------
! R1 R(1,2) 1.018 -DE/DX = 0.0 !
! R2 R(1,3) 1.018 -DE/DX = 0.0 !
! R3 R(1,4) 1.018 -DE/DX = 0.0 !
! A1 A(2,1,3) 105.7412 -DE/DX = 0.0 !
! A2 A(2,1,4) 105.7412 -DE/DX = 0.0 !
! A3 A(3,1,4) 105.7412 -DE/DX = 0.0 !
! D1 D(2,1,4,3) -111.8571 -DE/DX = 0.0 !
--------------------------------------------------------------------------------
NH3 Molecule |
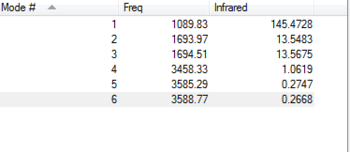
Questions and answers How many modes do you expect from the 3N-6 rule? 6 modes
Which modes are degenerate? Modes 2,3 and modes 5,6
Which modes are bending vibrations and which are bond stretch vibrations Bending vibrations = 1,2,3 Bond stretch vibrations = 4,5,6
Which mode is highly symmetric? 4
Which mode is the 'Umbrella' mode? 1
How many bands would you expect to see in an experimental spectrum of gaseous ammonia? At first i expected to see 6 peaks because there are six vibrational modes. Then I eliminated the modes with similar frequencies as these would essentially be the same peak on the spectrum and this resulted in 3 peaks. Looking at the vibrational intensity confirmed that there would be one very intense signal resulting from only one vibrational mode and the other peaks had a similar intensity which meant that there would be two peaks overall on the spectrum.
The charge on the N-atom is -1.125 and the charge on the H-atoms are 0.375. I would expect a negative charge for nitrogen as it is more electronegative than hydrogen and therefore pulls hydrogens electrons towards it. This in turn means that the hydrogen atoms would have a positive charge.
N2 Molecule
Calculation method: RB3LYP
Basis set: 6-31G(d,p)
Final energy: -109.52412868 a.u.
RMS gradient: 0.00000060 a.u.
Point group: D∞H
N-N Bond length: 1.10550 Angstroms
Item Value Threshold Converged?
Maximum Force 0.000001 0.000450 YES
RMS Force 0.000001 0.000300 YES
Maximum Displacement 0.000000 0.001800 YES
RMS Displacement 0.000000 0.001200 YES
Predicted change in Energy=-3.401026D-13
Optimization completed.
-- Stationary point found.
----------------------------
! Optimized Parameters !
! (Angstroms and Degrees) !
-------------------------- --------------------------
! Name Definition Value Derivative Info. !
--------------------------------------------------------------------------------
! R1 R(1,2) 1.1055 -DE/DX = 0.0 !
--------------------------------------------------------------------------------
The molecule is infrared inactive because when it absorbs infrared radiation, its vibrational modes do not result in a change in dipole moment.
N2 Molecule |
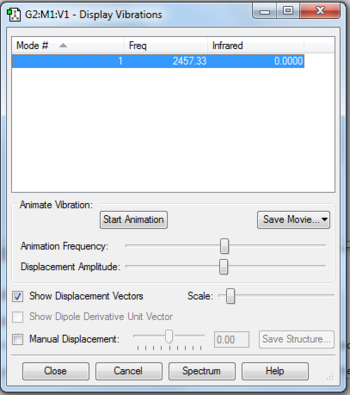
The N2 molecule is linear so the 3N-5 rule would apply
H2 Molecule
Key information
Calculation method: RB3LYP
Basis set: 6-31G(d.p)
Final energy: -1.17853936 a.u.
RMS gradient: 0.09719500 a.u.
Point group: D∞H
H-H Bond distance: 0.60000 Angstroms
Item Value Threshold Converged?
Maximum Force 0.000000 0.000450 YES
RMS Force 0.000000 0.000300 YES
Maximum Displacement 0.000000 0.001800 YES
RMS Displacement 0.000001 0.001200 YES
Predicted change in Energy=-1.164080D-13
Optimization completed.
-- Stationary point found.
----------------------------
! Optimized Parameters !
! (Angstroms and Degrees) !
-------------------------- --------------------------
! Name Definition Value Derivative Info. !
--------------------------------------------------------------------------------
! R1 R(1,2) 0.7428 -DE/DX = 0.0 !
--------------------------------------------------------------------------------
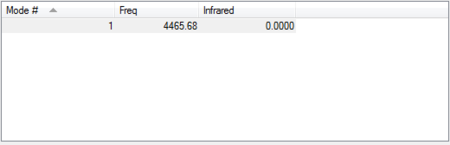
The molecule is infrared inactive because when it absorbs infrared radiation, its vibrational modes do not result in a change in dipole moment.
H2 Molecule |
Haber Bosch Process
The Haber Process is the main industrial procedure for making ammonia today and has revolutionized the agricultural industry. Before this process, the production of ammonia proved challenging and the main production methods were Birkeland-Edye process. E(NH3)= -56.55776842 a.u. 2*E(NH3)= -113.11553684 a.u. E(N2)= -109.52412868 a.u. E(H2)= -1.17853936 a.u. 3*E(H2)= -3.53561808 a.u. ΔE=2*E(NH3)-[E(N2)+3*E(H2)]= -113.11553684 - [-109.52412868 + -3.53561808] = -146.476855 kJ/mol The more stable is the ammonia product because energy is given in an exothermic fashion because the energy gained from forming the NH3 bonds is larger than breaking the H2 and N2 bonds.
The literature value obtained for the process is -92.44 kJ/mole. [1]
F2 Molecule
Key information
Calculation method: RB3LYP
Basis set: 6-31G(d.p)
Final energy: -199.42620785 a.u.
RMS gradient: 0.23253407 a.u.
Point group: D∞H
F-F Bond distance: 1.160000 Angstroms
Item Value Threshold Converged?
Maximum Force 0.000128 0.000450 YES
RMS Force 0.000128 0.000300 YES
Maximum Displacement 0.000156 0.001800 YES
RMS Displacement 0.000221 0.001200 YES
Predicted change in Energy=-1.995025D-08
Optimization completed.
-- Stationary point found.
----------------------------
! Optimized Parameters !
! (Angstroms and Degrees) !
-------------------------- --------------------------
! Name Definition Value Derivative Info. !
--------------------------------------------------------------------------------
! R1 R(1,2) 1.4028 -DE/DX = 0.0001 !
--------------------------------------------------------------------------------
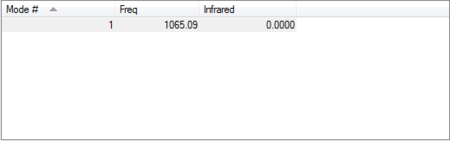
The molecule is infrared inactive because when it absorbs infrared radiation, its vibrational modes do not result in a change in dipole moment.
F2 Molecule |
This MO is interesting because it is non-bonding as the orbitals are too deep in energy to interact, but they are both in phase. They are too deep in energy because they are bound close to the nucleus and therefore the energies are -24.79730 kJ/mol. It involves the 1s orbital.
This MO shows bonding orbitals involving the 2s orbitals and has sigma symmetry. Bonding orbitals contribute to bonding.
This MO shows anti-bonding orbitals involving the 2s orbitals and has sigma symmetry. Anti-bonding orbitals do not contribute to bonding.
This MO is the LUMO. It involves the 3pz orbitals and is anti-bonding which means it does not contribute to bonding and it has sigma symmetry.
This MO is the HOMO. It involves the 3px orbitals and is bonding. This MO contributes to bonding and has pi symmerty too.
References
Ammonia production.[1]