Rep:Mod:man7286

Year 3 Computational Lab: Module 1

Emma Cassie

00556570

Introduction

Modern molecular modelling techniques can be used to accurately predict various properties of a molecule ranging from bond lengths and angles to more complicated spectroscopy results and MO diagrams. The main focus of the following projects is to predict the major product in a reaction with more than one outcome or to explain why one product is favoured over another.

Modelling Using Molecular Mechanics

The Hydrogenation of Cyclopentadiene Dimer

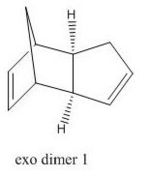
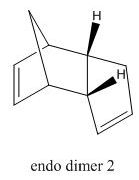
Cyclopentadiene readily dimerises by 4n+2 Diels Alder cycloaddition reaction, as shown in Figure 1, with the endo dimer (2) being favoured. As shown by the energies in Table 1 the endo dimer (2) is higher in energy by 2.11 kcal mol^-1, therefore in the dimerisation process the kinetic product is favoured.

Figure 1: Dimerisation of Cyclopentadiene

Figure 2: Hydrogenation of Dimer '2' to Hydrogenated Dimers 3 & 4

Table 1: MM2 Geometry Optimisation Results for Dimers 1&2 and Dihydrogenated Dimers 3&4

Energy/kcal mol-1
Stretch	1.29	1.25	1.28	1.10
Bend	20.58	20.85	19.90	14.52
Stretch-Bend	-0.84	-0.84	-0.84	-0.55
Torsion	7.66	9.51	10.77	12.50
Non-1,4 VDW	-1.42	-1.55	-1.22	-1.07
1,4 VDW	4.23	4.32	5.63	4.51
Dipole/Dipole	0.38	0.45	0.16	0.14
Total Energy	31.88	33.99	35.68	31.15

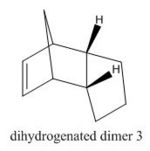
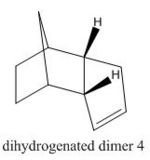
The hydrogenation of dimer 2 is shown in Figure 2. In the hydrogenation process one of the C=C bonds reacts readily whereas the tetrahydro- derivative is only formed after prolonged hydrogenation. Table 1 also shows that hydrogenation from 2 to dihydrogenated dimer 3 is disfavoured as the energy increases by 1.69 kcal mol^-1 whereas hydrogenation to dihydrogenated dimer 4 is favoured as the energy decreases by 2.84 kcal mol^-1, therefore dihydrogenated dimer 4 is the major product under thermodynamic conditions.

Stereochemistry of Nucleophilic Additions to a Pyridinium Ring

Figure 3: Reaction of Molecule 5 with MeMgI

Figure 5: angle between carbonyl and aromatic ring- molecule 5

Figure 4: Reaction of Molecule 7 with PhNH₂

Figure 6: angle between carbonyl and aromatic ring- molecule 7

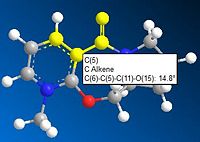
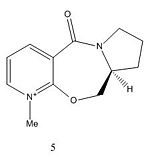
The reaction between molecule 5 and MeMgI is shown in Figure 3. Figure 5 shows that the angle between the carbonyl and aromatic ring in molecule 5 to be 14.8° and by looking at the 3D model of molecule 5 the carbonyl is seen to be pointing upwards. On reaction with MeMgI the magnesium atom chelates to the carbonyl oxygen so the methyl group is added to the pyridinium ring also pointing upwards. This chelation makes the reaction regio- and stereoselective. In this specific reaction addition to the para-carbon is 95% regioselective and 100% stereoselective.

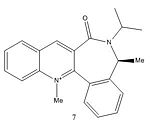
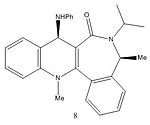
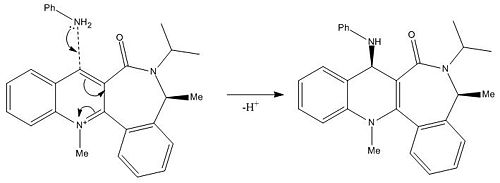
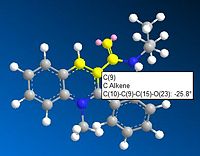
Figure 4 shows the reaction between molecule 7 and PhNH₂. Figure 6 shows that the angle between the carbonyl and the aromatic ring in molecule 7 is -25.8° and the 3D model of molecule 7 shows that the carbonyl is pointing downwards. When the bulky PhNH₂ attacks it does this from above, on the less hindered face, therefore in the major product molecule 8 the PhNH group is pointing upwards.

Table 2: MM2 Geometry Optimisation Results for Pyridinium Reactants and Products

Energy/kcal mol-1
Stretch	2.36	2.53	4.13	5.72
Bend	14.73	16.93	11.82	30.04
Stretch-Bend	0.19	0.38	0.45	0.94
Torsion	5.84	5.89	11.65	5.52
Non-1,4 VDW	0.08	0.28	4.40	8.19
1,4 VDW	17.17	18.37	29.80	36.13
Charge/Dipole	11.31	n/a	10.53	n/a
Dipole/Dipole	-7.60	-8.22	-8.54	-6.51
Total Energy	44.08	36.16	64.24	80.03

Stereochemistry and Reactivity of an Intermediate in the Synthesis of Taxol

Table 3: MM2 Geometry Optimisation Results for Taxol Synthesis Intermediates

	Molecule 9	Molecule 9 + H2	Molecule 10	Molecule 10 + H2
Energy/kcal mol-1
Stretch	2.82	2.85	3.22	3.16
Bend	16.43	22.27	13.47	19.44
Stretch-Bend	0.46	0.72	0.42	0.06
Torsion	21.37	22.67	23.78	21.69
Non-1,4 VDW	-0.87	-2.66	0.01	0.35
1,4 VDW	14.03	17.93	14.93	16.97
Dipole/Dipole	0.14	0.00	-0.01	0.00
Total Energy	54.35	63.78	55.82	61.67

In both cases the alkene is more stable than the corresponding alkane making them hyperstable alkenes, therefore these alkenes react slowly.

Modelling Using Semi-Empirical Molecular Orbital Theory

Regioselective Addition of Dichlorocarbene

Figure 7: IR Spectrum of Molecule 12

Figure 8: IR Spectrum of Molecule 12 + H₂

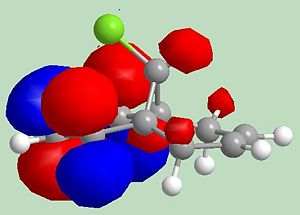
Molecule 12: heat of formation = 19.74 kcal mol^-1 (MOPAC/PM6 MO method)

HOMO: LUMO:

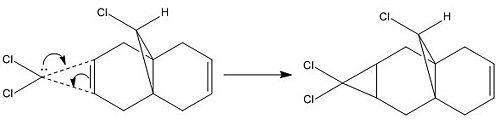
Addition of dichlorocarbene is like electrophilic addition. As seen above the HOMO for molecule 12 has most electron density on the alkene on the same side as the chlorine, therefore electrophilic addition will be prefered on the left-hand alkene. The product of the reaction between molecule 12 and dichlorocarbene is shown below.

Figure 9: Proposed Reaction of Molecule 12 with Dichlorocarbene

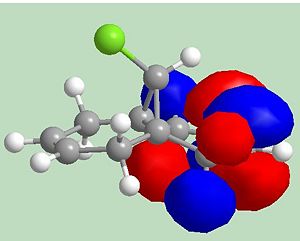
Molecule 12 + H₂: heat of formation = -2.43 kcal mol^-1 (MOPAC/PM6 MO method)

Table 4: Streching Frequencies

Bond
C-Cl	771	775
C=C left	1757	1758
C=C right	1737	n/a

The IR streches for C-Cl and C=C in molecule 12 and its hydrogenated counterpart are very similar which means the hydrogenation doesn't have a very big effect on the overall shape of the molecule.

Mini-Project: Reaction of an Azido Sulfonate with DAST

Figure 11: ¹⁹F NMR of Equatorial Product DOI:10042/to-7375

Figure 12: ¹⁹F NMR of Axial Product DOI:10042/to-7376

Figure 13: Dihedral Angles and Coupling Constants on Equatorial Product

Figure 14: Dihedral Angles and Coupling Constants on Axial Product

Figure 10: Reaction Scheme

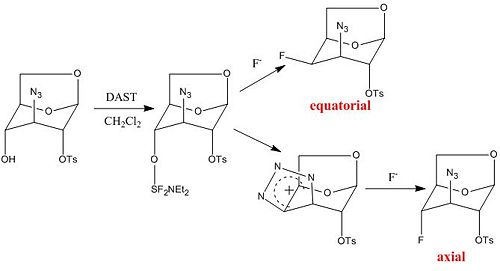
Starting material: [(1R,2S,3S,4R,5R)-3-azido-2-hydroxy-6,8-dioxabicyclo[3.2.1]octan- 4-yl] 4-methylbenzenesulfonate

Equatorial product:

Axial product:

Table 5: Comparison Between Calculated and Literature Values

	Equatorial Product		Axial Product
	Calculated	Literature	Calculated	Literature
δ/ppm	-404.4	-202.0	-385.2	-178.9
3JH3-H4/Hz	1.9	4.7	1.0	3.7
3JH4-H5/Hz	7.0	4.7	2.1	1.5

As seen in Table 5 the calculated values match the pattern of the literature values i.e. the chemical shift for the equatorial product is more negative than for the axial product but the calculated values are much higher. The same can be said for the J coupling values. Because of this and the limited time remaining I chose to persue one of the preset mini projects.

Mini Project (2): Stereoselective Dissolving Metal Reductions

Figure 15: Stereoselective Dissolving Metal Reduction of a Bicyclic Ketone

Figure 16: Proposed Mechanism for Dissolving Metal Reduction

Figure 17: Numbers for NMR Assignment

Figure 18: ¹³C NMR of Starting Material

Figure 19: ¹³C NMR of Product

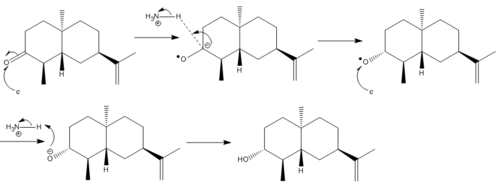
Firstly both starting material and product geometries were optimized using MPW1PW91/6-31G(D,P) Gaussian method. The 13C NMR spectrum for the product was predicted and the comparison between these results and the literature is shown in Table 6.

Optimized geometries:

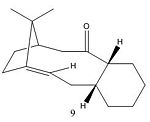
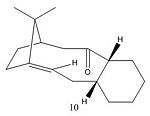
The reaction produces the alcohol in the down position because in the trigonal planar intermediate the configuration of the 6C ring means that the top face is less hindered when the H⁺ from ammonia comes in, it therefore comes in on the top face, pushing the oxygen into the down position.

Table 6: Comparison Between Calculated and Literature Values

	Starting Material		Product
δ/ppm	Calculated	Literature	Calculated	Literature
C1	39.2	38.2	30.4	30.9
C2	208.3	213.3	75.0	76.9
C3	47.4	45.2	41.7	38.9
C4	48.0	45.7	45.3	43.2
C5	34.3	34.0	34.5	33.8
C6	42.7	41.7	40.0	39.9
C7	30.9	27.5	32.8	26.1
C8	41.5	38.3	40.5	39.2
C9	27.5	23.0	24.9	23.1
C10	40.2	36.3	33.8	37.1

The main proof that the reaction was successful is the chemical shift for carbon 2 which decreases by over 100pm, this is because the reduction of the carbonyl to the alcohol means that the carbon is less deshielded.