Rep:Mod:ma777
Information about various molecules
This wiki page summaries information about various molecules after optimization, the information below for the molecules studied was found by using the Gaussian software and the molecules were created using the Gaussview software. The molecules that were analyzed using these software packages were NH3, N2, H2, trans HFC=CHF and cis HFC=CHF. In addition a Haber-Bosch calculation was also done to determine if the creation of NH3 from N2 and H2 was thermodynamically favorable.
NH3molecule
Below is all the information discovered about a NH3 molecule from using the Gaussian and Gaussview software.
General information
Below is general information about the optimized NH3 that was obtained through Gaussian after the molecule was created through Gaussview:
Calculation method: RB3LYP
Basis set: 6-31G(d.p)
Final energy: -56.55776873 au
RMS gradient: 0.00000485 au
Point group: C3v
N-H bond length: 1.01798 Angstroms
H-N-H bond angle: 105.741 degrees
'item' table and optimization file
The below table shows that the optimization was completed for NH3:
Item Value Threshold Converged? Maximum Force 0.000004 0.000450 YES RMS Force 0.000004 0.000300 YES Maximum Displacement 0.000072 0.001800 YES RMS Displacement 0.000035 0.001200 YES
Below is the link for the file showing the optimization of the NH3 molecule from Gaussian: Optimization link
Jmol image of optimized NH3
This image shows the final optimized NH3 molecule:
NH3 molecule |
Vibrational analysis
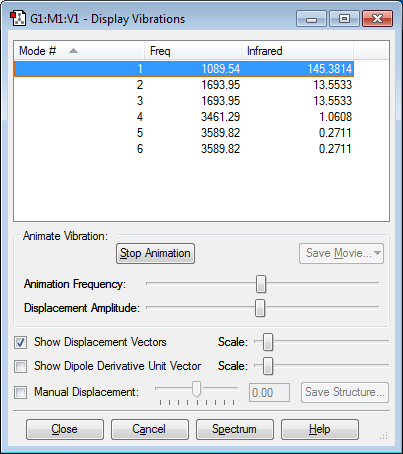
Below is an image showing the various vibrational modes of NH3:
There are no negative frequencies in the table showing the optimization was successful.
Below are the answers to questions about the vibrations of NH3:
From the 3N-6 rule there are 6 vibrations expected as (3*4)-6=6.
Modes 2 and 3 and 5 and 6 are degenerate due to them having the same frequency values.
Modes 1,2 and 3 are bending vibrations and modes 4,5 and 6 are stretching vibrations.
Mode 4 is highly symmetric.
The umbrella mode is mode 1.
In the experimental section of gaseous ammonia there would be expected to be 3 bands present because modes 4, 5 and 6 will merge into one because of their similar frequency and infrared values, however this band may not be presented because of the very small frequency values observed. Meanwhile modes 2 and 3 are at the same frequency which will produce one bands. Overall the 3 bands show mode 1, modes 2 and 3 and modes 4,5 and 6.
Charge analysis
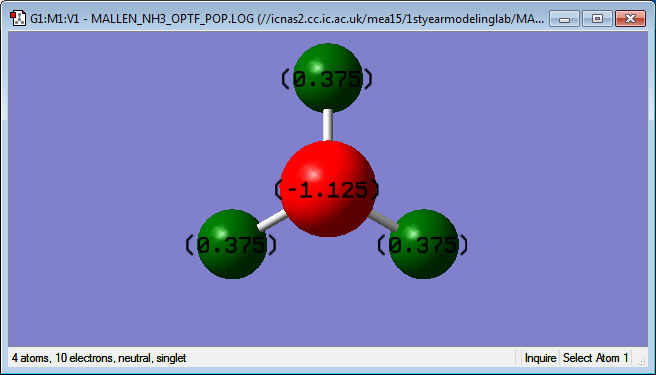
Below is an image showing the charges on the NH3 molecule:
The image above matches what charge values are expected in the NH3 molecule due to the nitrogen being more electronegative then the hydrogen's and so it pulls electrons towards it which means it becomes slightly negative while the hydrogen's will become slightly positive due to the electrons being pulled away from them.
N2molecule
Below is all the information discovered about a N2 molecule from using the Gaussian and Gaussview software.
General information
Below is general information about the optimized N2 that was obtained through Gaussian after the molecule was created through Gaussview:
Calculation method: RB3LYP
Basis set: 6-31G(d.p)
Final energy: -109.52412868 au
RMS gradient: 0.00000060 au
Point group: D∞h
N-N bond length: 1.10550 Angstroms
The molecule is also a linear shape
'item' table and optimization file
The below table shows that the optimization was completed for N2:
Item Value Threshold Converged? Maximum Force 0.000001 0.000450 YES RMS Force 0.000001 0.000300 YES Maximum Displacement 0.000000 0.001800 YES RMS Displacement 0.000000 0.001200 YES
Below is the link for the file showing the optimization of the N2 molecule from Gaussian: Optimization link
Jmol image of optimized N2
This image shows the final optimized N2 molecule:
N2 molecule |
Vibrational analysis
Below is an image showing the various vibrational modes of N2:
The image above shows there is one vibrational mode for the N2 molecule which matches expectations as there is only one bond which means the vibrational mode is caused by this bond stretching. There are also no negative frequencies in the table showing the optimization was successful.
Charge analysis
The charges on N2 will be 0 on each atom because the structure consists of two of the same atom so therefore the the electronegativities are the same and so the electrons are distributed evenly leading to no polarity.
H2molecule
Below is all the information discovered about a H2 molecule from using the Gaussian and Gaussview software.
General information
Below is general information about the optimized H2 that was obtained through Gaussian after the molecule was created through Gaussview:
Calculation method: RB3LYP
Basis set: 6-31G(d.p)
Final energy: -1.17853936 au
RMS gradient: 0.00000017 au
Point group: D∞h
H-H bond length: 0.74279 Angstroms
The molecule is also a linear shape
'item' table and optimization file
The below table shows that the optimization was completed for H2:
Item Value Threshold Converged? Maximum Force 0.000000 0.000450 YES RMS Force 0.000000 0.000300 YES Maximum Displacement 0.000000 0.001800 YES RMS Displacement 0.000001 0.001200 YES
Below is the link for the file showing the optimization of the H2 molecule from Gaussian: Optimization link
Jmol image of optimized H2
This image shows the final optimized H2 molecule:
H2 molecule |
Vibrational analysis
Below is an image showing the various vibrational modes of H2:
The image above shows there is one vibrational mode for the H2 molecule which matches expectations as there is only one bond which means the vibrational mode is caused by this bond stretching. There are also no negative frequencies in the table showing the optimization was successful.
Charge analysis
The charges on H2 will be 0 on each atom because the structure consists of two of the same atom so therefore the the electronegativities are the same and so the electrons are distributed evenly leading to no polarity.
Haber-Bosch process
The Haber-Bosch process converts hydrogen and nitrogen into ammonia by the reaction below:
N2 + 3H2 -> 2NH3
The energy of the chemical reaction is reported below:
E(NH3)= -56.55776873 au 2*E(NH3)= -113.1155375 au E(N2)= -109.52412868 au E(H2)= -1.17853936 au 3*E(H2)= -3.53561808 au ΔE=2*E(NH3)-[E(N2)+3*E(H2)]= -0.05579074 ΔE= -146.48 KJ/mol
The ammonia is more stable than the nitrogen and hydrogen as shown by the negative sign in the reaction which shows it is a exothermic process.
This value is in a similar range to value reported by Asbjørn Klerke,Claus Hviid Christensen,Jens K. Nørskovand and Tejs Vegge[1] in the journal article Ammonia for hydrogen storage: challenges and opportunities. The value reported is -46KJ/mol, this value could be different as the data obtained by the Gaussian software is only theoretical and will not take into account interactions that will take place in experimental conditions which could cause the NH3 bonds to be weaker or the H2 and N2 bonds to be stronger causing a smaller energy change to be observed.
Trans HFC=CHF molecule
Below is all the information discovered about a trans HFC=CHF molecule from using the Gaussian and Gaussview software.
General information
Below is general information about the optimized trans HFC=CHF that was obtained through Gaussian after the molecule was created through Gaussview:
Calculation method: RB3LYP
Basis set: 6-31G(d.p)
Final energy: -277.04429428 au
RMS gradient: 0.00022226 au
Point group: C2h
C-H bond length: 1.08393 Angstroms
C-F bond length 1.34630 Angstroms
C=C bond length 1.32645 Angstroms
H-C-F bond angle 114.717 degrees
'item' table and optimization file
The below table shows that the optimization was completed for trans HFC=CHF:
Item Value Threshold Converged? Maximum Force 0.000324 0.000450 YES RMS Force 0.000143 0.000300 YES Maximum Displacement 0.000569 0.001800 YES RMS Displacement 0.000342 0.001200 YES
Below is the link for the file showing the optimization of the trans HFC=CHF molecule from Gaussian: Optimization link
Jmol image of optimized trans HFC=CHF
This image shows the final optimized HFC=CHF molecule in its trans isomer form:
Trans HFC=CHF molecule |
Vibrational analysis
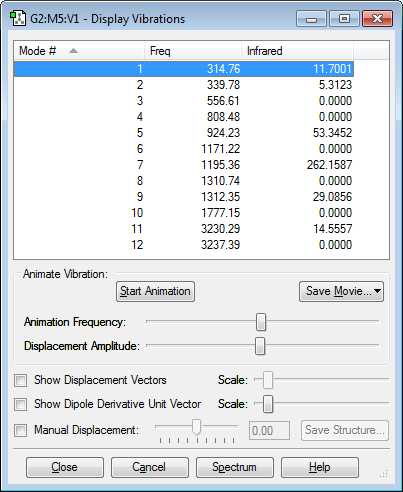
Below is an image showing the various vibrational modes of trans HFC=CHF:
The vibrations show that trans HFC=CHF has many bending and stretching modes of vibration. From the 3N-6 rule there is expected to be 12 modes of vibrations as (3*6)-6=12 which is the number of vibrations shown by the image above. Modes 11 and 12 correspond to the hydrogen-carbon bonds stretching, this matches common C-H bond stretching values. Mode 10 shows a C=C bond stretch which matches the frequency expected. modes 8 and 9 show C-H bond bending. The other modes all fall into the fingerprint region of the molecule as they are all complex vibrations of the molecule. There are also no negative frequencies in the table showing the optimization was successful.
Charge analysis
Below is an image showing the charges on the trans HFC=CHF molecule:
The charge values are what are expected because the fluorine atoms are the most electronegative atoms in the molecule and so will draw electrons towards them which will cause them to have partial negative charge. The carbon was also predicted to have a lower charge value than the hydrogen as carbon is slightly more electronegative when compared to hydrogen.
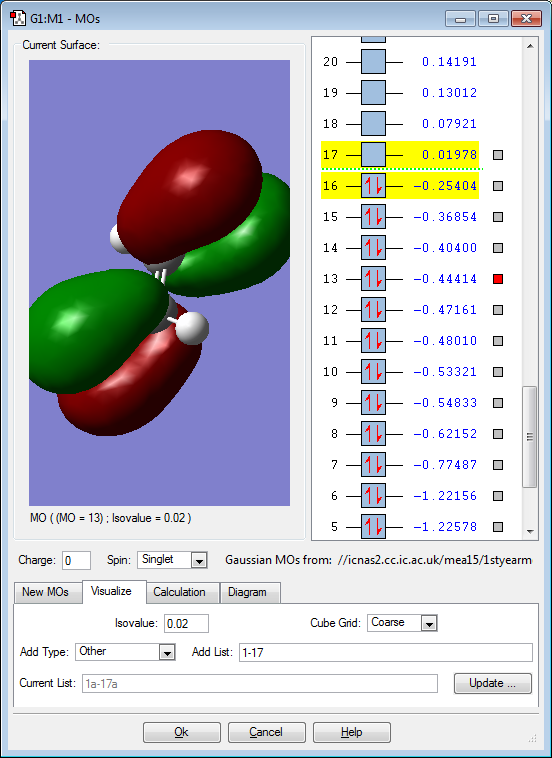
Molecular orbitals
Below are images that show the various molecular orbitals of trans HFC=CHF:
The above image shows the 1s orbital for the fluorine atoms, the orbitals do not interact with anything because it is so low in energy when compared to the other orbitals. The orbitals on the fluorine atoms 1s orbitals are also out of phase with each other. This is an occupied molecular orbital.
The above image shows the 1s orbitals for the carbon atoms, the orbitals do not interact with the other orbitals present due to the low energy of the orbital when compared to the other orbitals. The orbitals are in phase with each other. This is an occupied molecular orbital.
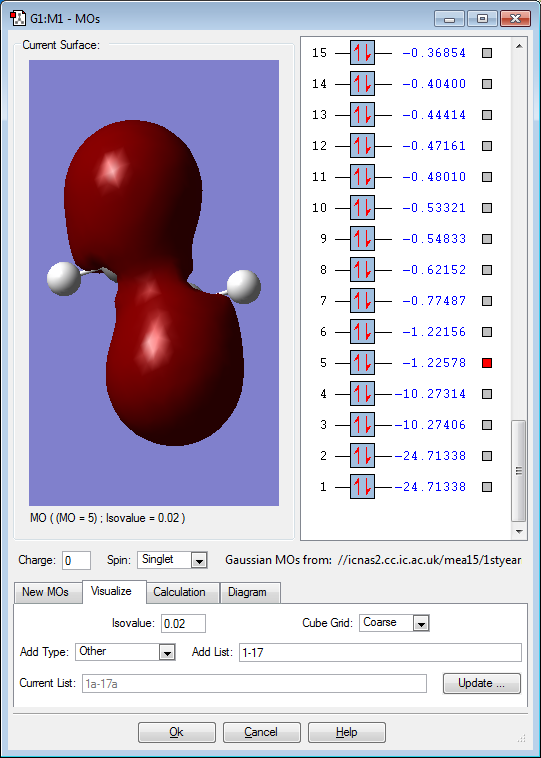
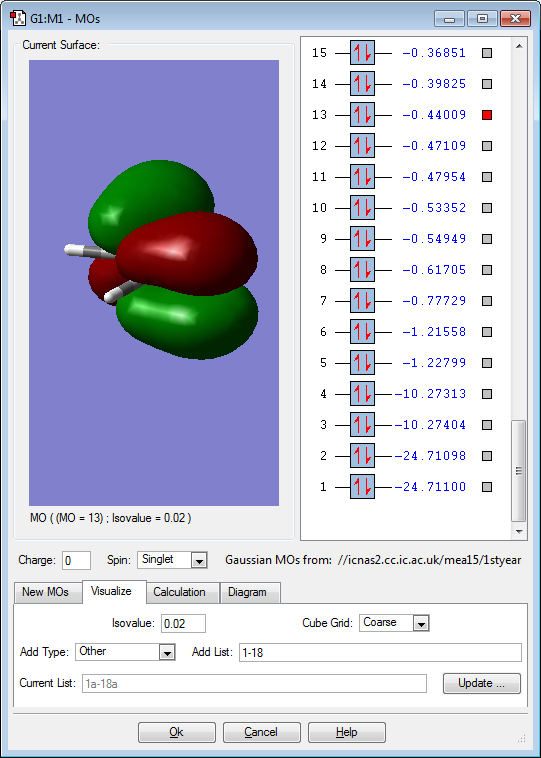
The above image shows a sigma bond between the fluorine and carbon atoms and a sigma bond between the two carbon atoms due to the electron density encompassing all of these bonds. The fluorine and carbon sigma bonds are between the 2s orbitals on carbon and the 2s orbitals on the fluorine. The sigma bond between the carbon atoms is between the 2s orbital on the fluorine. The electron density of the occupied molecular orbital is towards the sigma bonds between the carbon and fluorine due to the fluorine being electronegative and so some of the carbon-carbon sigma bond electron density is pulled toward the fluorine atoms. The molecular orbital is not deep lying but it is not in the HOMO/LUMO region.
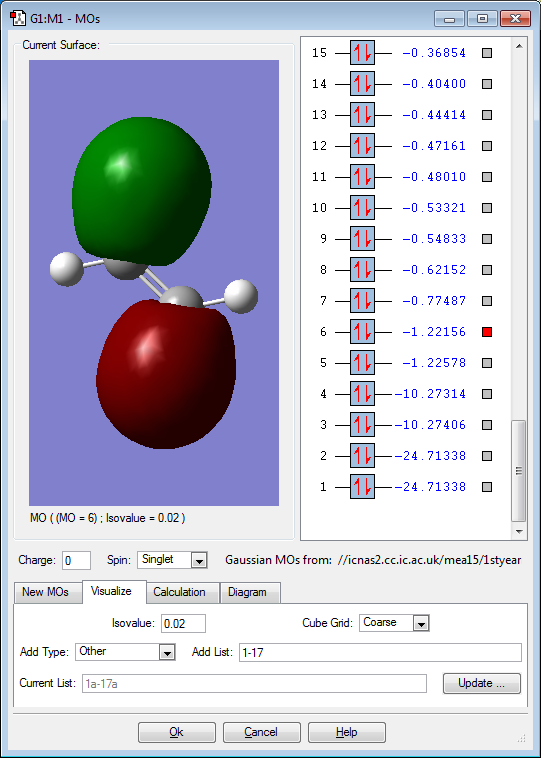
The above image shows the anti-bonding sigma bond between the carbon and fluorine atoms. This is the anti bonding sigma orbital between the carbon and fluorine atoms because it is a slightly higher energy when compared to the bonding orbital. In addition the electron density also occurs in the same regions as the occupied molecular orbital. The atomic orbitals involved are the 2s orbital on the fluorine and the 2s orbital on the carbon. The molecular orbital is not deep lying but it is not in the HOMO/LUMO region.
The above image shows pi interactions between the 2p fluorine orbitals and the 2p carbon orbitals. The molecular orbital shows the electron density is positioned towards the fluorine atoms due to them being more electronegative than the carbon atoms. The molecular orbital is also in the HOMO/LUMO region as it has a similar energy value to the HOMO/LUMO. This molecular orbital is occupied but it must have an anti bonding orbital as the overall structure of the molecule does not have a pi bond between the carbon and fluorine atoms.
Cis HFC=CHF molecule
Below is all the information discovered about a cis HFC=CHF molecule from using the Gaussian and Gaussview software.
General information
Below is general information about the optimized cis HFC=CHF that was obtained through Gaussian after the molecule was created through Gaussview:
Calculation method: RB3LYP
Basis set: 6-31G(d.p)
Final energy: -277.04432306 au
RMS gradient: 0.00003730 au
Point group: CS
C-H bond length: 1.08357 Angstroms
C-F bond length 1.34279 Angstroms
C=C bond length 1.32692 Angstroms
H-C-F bond angle 114.685 degrees
'item' table and optimization file
The below table shows that the optimization was completed for cis HFC=CHF:
Item Value Threshold Converged? Maximum Force 0.000090 0.000450 YES RMS Force 0.000035 0.000300 YES Maximum Displacement 0.000302 0.001800 YES RMS Displacement 0.000142 0.001200 YES
Below is the link for the file showing the optimization of the cis HFC=CHF molecule from Gaussian: Optimization link
Jmol image of optimized cis HFC=CHF
This image shows the final optimized HFC=CHF molecule in its cis isomer form:
Cis HFC=CHF molecule |
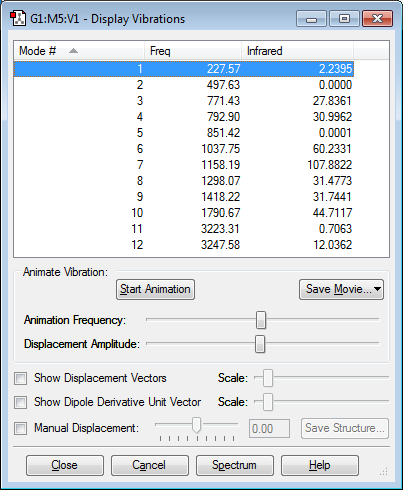
Vibrational analysis
Below is an image showing the various vibrational modes of cis HFC=CHF:
The vibrations show that cis HFC=CHF has many bending and stretching modes of vibration. From the 3N-6 rule there is expected to be 12 modes of vibrations as (3*6)-6=12 which is the number of vibrations shown by the image above. Modes 11 and 12 correspond to the hydrogen-carbon bonds stretching, this matches common C-H bond stretching values. Mode 10 shows a C=C bond stretch which matches the frequency expected. modes 8 and 9 show C-H bond bending. The other modes all fall into the fingerprint region of the molecule as they are all complex vibrations that involve the whole molecule. There are also no negative frequencies in the table showing the optimization was successful.
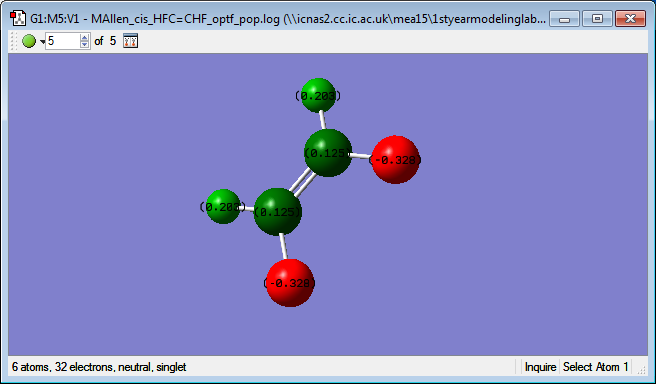
Charge analysis
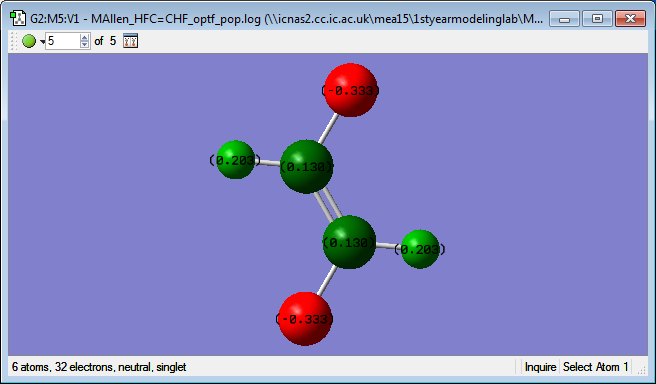
Below is an image showing the charges on the cis HFC=CHF molecule:
The charge values are what are expected because the fluorine atoms are the most electronegative atoms in the molecule and so will draw electrons towards them which will cause them to have partial negative charge. The carbon was also predicted to have a lower charge value than the hydrogen as carbon is slightly more electronegative when compared to hydrogen.
Molecular orbitals
Below are images that show the various molecular orbitals of cis HFC=CHF:
The above image shows the 1s orbital for the fluorine atoms, the orbitals do not interact with anything because it is so low in energy when compared to the other orbitals. The orbitals on the fluorine atoms 1s orbitals are also out of phase with each other. This is an occupied molecular orbital.
The above image shows the 1s orbitals for the carbon atoms, the orbitals do not interact with the other orbitals present due to the low energy of the orbital when compared to the other orbitals. The orbitals are in phase with each other. This is an occupied molecular orbital.
The above image shows a sigma bond between the fluorine and carbon atoms and a sigma bond between the two carbon atoms due to the electron density encompassing all of these bonds. The fluorine and carbon sigma bonds are between the 2s orbitals on carbon and the 2s orbitals on the fluorine. The sigma bond between the carbon atoms is between the 2s orbital on the fluorine. The electron density of the occupied molecular orbital is towards the sigma bonds between the carbon and fluorine due to the fluorine being electronegative and so some of the carbon-carbon sigma bond electron density is pulled toward the fluorine atoms, this means there is very little electron density on the carbon-carbon sigma bond on the hydrogen side of the molecule. The molecular orbital is not deep lying but it is not in the HOMO/LUMO region.
The above image shows the anti-bonding sigma bond between the carbon and fluorine atoms. This is the anti bonding sigma orbital between the carbon and fluorine atoms because it is a slightly higher energy when compared to the bonding orbital. In addition the electron density also occurs in the same regions as the occupied molecular orbital. The atomic orbitals involved are the 2s orbital on the fluorine and the 2s orbital on the carbon. The molecular orbital is not deep lying but it is not in the HOMO/LUMO region.
The above image shows pi interactions between the 2p fluorine orbitals and the 2p carbon orbitals. The molecular orbital shows the electron density is positioned towards the fluorine atoms due to them being more electronegative than the carbon atoms. The molecular orbital is also in the HOMO/LUMO region as it has a similar energy value to the HOMO/LUMO. This molecular orbital is occupied but it must have an anti bonding orbital as the overall structure of the molecule does not have a pi bond between the carbon and fluorine atoms.
Comparisons between the cis and trans isomers of HFC=CHF
From the data gathered above it can be seen that there are minor differences between the cis and trans form of HFC=CHF. The main differences between the isomers are that that they have different molecular orbital orientations and different points groups due to the positioning of the fluorine atoms. The charges and vibrations also show slight differences but this could be due to the Gaussian optimizing software producing slight variances in its calculations.
References
- ↑ http://dcwww.camd.dtu.dk/Nabiit/Ammonia%20for%20hydrogen%20storage%20-%20challenges%20and%20opportunities.pdf Klerke A, Christensen CH, Nørskov JK, Vegge T. Ammonia for hydrogen storage: challenges and opportunities. Journal of Materials Chemistry. 2008;18(20):2304-10.