Rep:Mod:lp2015
NH3 molecule
Calculation Method: RB3LYP
Basis Set: 6-31G(d.p)
Final Energy E(RB3LYP): -56.55776873 a.u.
RMS Gradient Norm: 0.00000485 a.u.
Point Group: C3V
N-H bond distance = 1.01798 ångström
H-N-H bond angle = 105.741 °
test molecule |
The optimisation file is liked to here
Item Value Threshold Converged?
Maximum Force 0.000006 0.000450 YES
RMS Force 0.000004 0.000300 YES
Maximum Displacement 0.000014 0.001800 YES
RMS Displacement 0.000009 0.001200 YES
Predicted change in Energy=-1.141676D-10
Optimization completed.
-- Stationary point found.
----------------------------
! Optimized Parameters !
! (Angstroms and Degrees) !
-------------------------- --------------------------
! Name Definition Value Derivative Info. !
--------------------------------------------------------------------------------
! R1 R(1,2) 1.018 -DE/DX = 0.0 !
! R2 R(1,3) 1.018 -DE/DX = 0.0 !
! R3 R(1,4) 1.018 -DE/DX = 0.0 !
! A1 A(2,1,3) 105.7446 -DE/DX = 0.0 !
! A2 A(2,1,4) 105.7446 -DE/DX = 0.0 !
! A3 A(3,1,4) 105.7446 -DE/DX = 0.0 !
! D1 D(2,1,4,3) -111.8637 -DE/DX = 0.0 !
--------------------------------------------------------------------------------
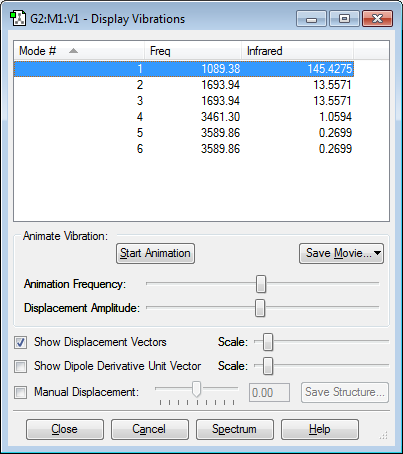
Vibration Modes
Number of modes from the 3N-6 rule: 6 Modes
Degenerate Modes: Modes 2 & 3, Modes 5 & 6
"Bending" Vibrations Modes: Modes 1,2 & 3
"Bond Stretch" Vibrations Modes: Modes 4, 5 & 6
Highly Symmetric Mode: Mode 4
"Umbrella" Mode: Mode 1
Number of Bands Expected in Experimental Spectrum of Gaseous Ammonia: 4 Bands
Charge Distribution of Atoms in NH3
Charge of Nitrogen Atom: -1.125
Charge of Hydrogen Atoms: 0.375
A positive charge was expected of Hydrogen atoms and negative charge for Nitrogen atom, this is because the electronegativity of Nitrogen atom is greater than that of Hydrogen atoms, hence it draws the electron cloud of Hydrogen atoms to itself, making it more negative. The electron cloud of Hydrogen atoms are pulled away from their nuclei, making them possessing a positive charge.
N2 molecule
Calculation Method: RB3LYP
Basis Set: 6-31G(d.p)
Final Energy E(RB3LYP): -109.52412868 a.u.
RMS Gradient Norm: 0.00000060 a.u.
Point Group: D*H
N-N bond distance = 1.10550 ångström
N-N bond angle = 180.000 °
test molecule |
The optimisation file is liked to here
Item Value Threshold Converged?
Maximum Force 0.000001 0.000450 YES
RMS Force 0.000001 0.000300 YES
Maximum Displacement 0.000000 0.001800 YES
RMS Displacement 0.000000 0.001200 YES
Predicted change in Energy=-3.401031D-13
Optimization completed.
-- Stationary point found.
----------------------------
! Optimized Parameters !
! (Angstroms and Degrees) !
-------------------------- --------------------------
! Name Definition Value Derivative Info. !
--------------------------------------------------------------------------------
! R1 R(1,2) 1.1055 -DE/DX = 0.0 !
--------------------------------------------------------------------------------
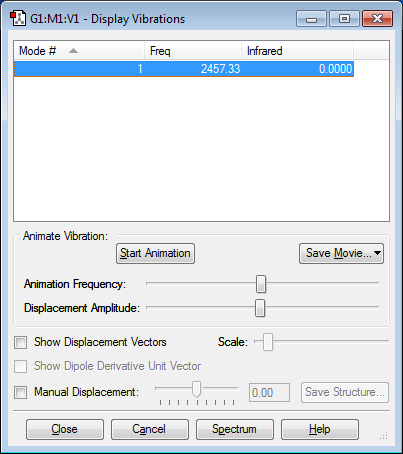
Vibration Modes
Number of Vibration Modes: 1 Mode
H2 molecule
Calculation Method: RB3LYP
Basis Set: 6-31G(d.p)
Final Energy E(RB3LYP): -1.17853936 a.u.
RMS Gradient Norm: 0.00000017 a.u.
Point Group: D*H
H-H bond distance = 0.74279 ångström
H-H bond angle = 180.000 °
H2 Molecule |
The optimisation file is liked to here
Item Value Threshold Converged?
Maximum Force 0.000000 0.000450 YES
RMS Force 0.000000 0.000300 YES
Maximum Displacement 0.000000 0.001800 YES
RMS Displacement 0.000001 0.001200 YES
Predicted change in Energy=-1.164080D-13
Optimization completed.
-- Stationary point found.
----------------------------
! Optimized Parameters !
! (Angstroms and Degrees) !
-------------------------- --------------------------
! Name Definition Value Derivative Info. !
--------------------------------------------------------------------------------
! R1 R(1,2) 0.7428 -DE/DX = 0.0 !
--------------------------------------------------------------------------------
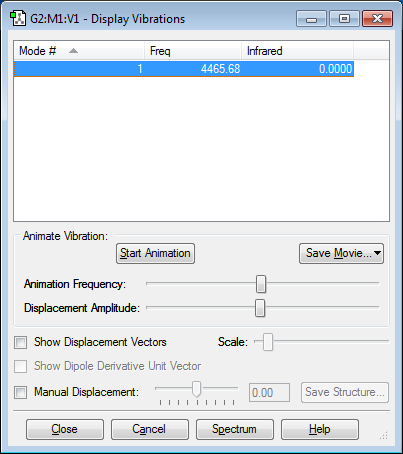
Vibration Modes
Number of Vibration Modes: 1 Mode
Haber-Bosch Process
N2 + 3H2 -> 2NH3
E(NH3) = -56.55776873 Hartrees
2*E(NH3) = -113.11553746 Hartrees
E(N2) = -109.52412868 Hartrees
E(H2) = -1.17853936 Hartrees
3*E(H2) = -3.53561808 Hartrees
ΔE = 2*E(NH3)-[E(N2)+3*E(H2)] = -146.478494 kJ/mol (-0.0557907 Hartrees)
Literature value of ΔE = -92.4 kJ/mol
The theoretical calculated ΔE value is close to the experimental literature value, the difference may be due to the mixture of higher and lower energy of the reactants and product molecules involved in the experimental reaction, whereas the theoretical value only considered the lowest energy of the molecules involved, hence there is a difference in ΔE.
As the Haber-Bosch Process has a negative standard enthalpy of reaction value, the reaction is exothermic, Hence, the energy of gaseous ammonia is lower than the energies of its elemental reactants, hence the gaseous ammonia product is more stable.
H2CO molecule
Calculation Method: RB3LYP
Basis Set: 6-31G(d.p)
Final Energy E(RB3LYP): -114.50319933 a.u.
RMS Gradient Norm: 0.00007386 a.u.
Point Group: CS
C-H bond distance = 1.11057 ångström
C=O bond distance = 1.20676 ångström
H-C-H bond angle = 32.391 °
H-C=O bond angle = 122.395 °
test molecule |
The optimisation file is liked to here
Item Value Threshold Converged?
Maximum Force 0.000197 0.000450 YES
RMS Force 0.000085 0.000300 YES
Maximum Displacement 0.000270 0.001800 YES
RMS Displacement 0.000149 0.001200 YES
Predicted change in Energy=-3.772184D-08
Optimization completed.
-- Stationary point found.
----------------------------
! Optimized Parameters !
! (Angstroms and Degrees) !
-------------------------- --------------------------
! Name Definition Value Derivative Info. !
--------------------------------------------------------------------------------
! R1 R(1,2) 1.1106 -DE/DX = -0.0001 !
! R2 R(1,3) 1.1106 -DE/DX = -0.0001 !
! R3 R(1,4) 1.2068 -DE/DX = -0.0002 !
! A1 A(2,1,3) 115.2188 -DE/DX = 0.0 !
! A2 A(2,1,4) 122.3859 -DE/DX = 0.0 !
! A3 A(3,1,4) 122.3954 -DE/DX = 0.0 !
! D1 D(2,1,4,3) 180.0 -DE/DX = 0.0 !
--------------------------------------------------------------------------------
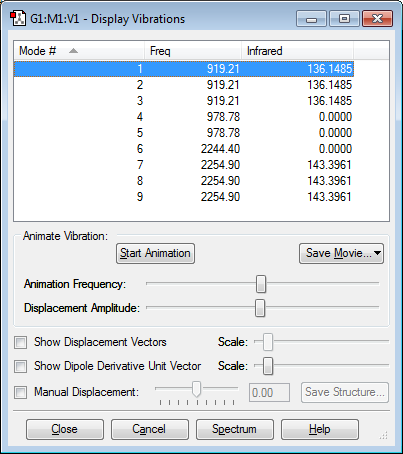
Vibration Modes of H2CO
Number of vibration modes: 6
Number of Bands Expected in Experimental Spectrum of Gaseous Methanal: 6
Charge Distribution of Atoms in H2CO
Charge of Oxygen Atom: -0.494
Charge of Carbon Atom: 0.221
Charge of Hydrogen Atoms: 0.137
A positive charge was expected of Hydrogen and Carbon atoms and negative charge for Oxygen atom, this is because the electronegativity of Oxygen atom is greater than that of Hydrogen or Carbon atoms, hence it draws the electron cloud of Carbon and Hydrogen atoms to itself, making it more negative. The electron cloud of Carbon and Hydrogen atoms are pulled away from their nuclei, making them possessing a positive charge. The positive charge of Carbon atom is greater than that of Hydrogen atoms because the Carbon is directly bonded to the electronegative Oxygen atom, hence the electron cloud of the Carbon atom is more distorted and pulled towards the Oxygen atom more than that of Hydrogen atoms.
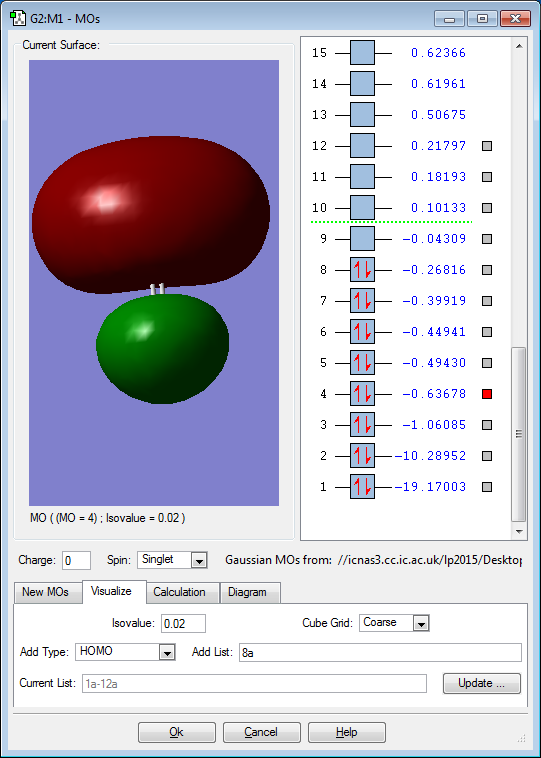
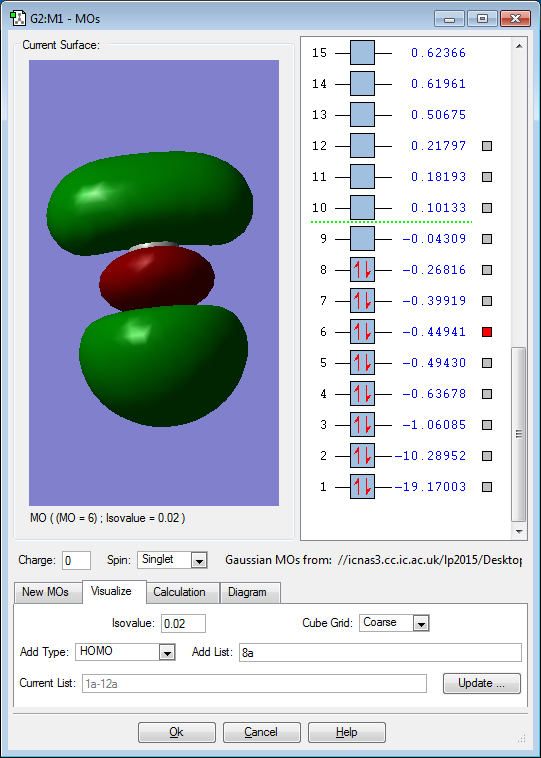
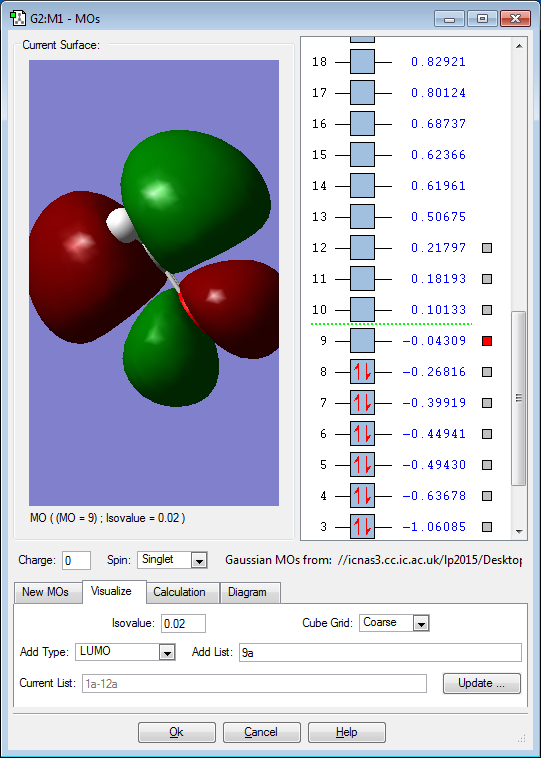
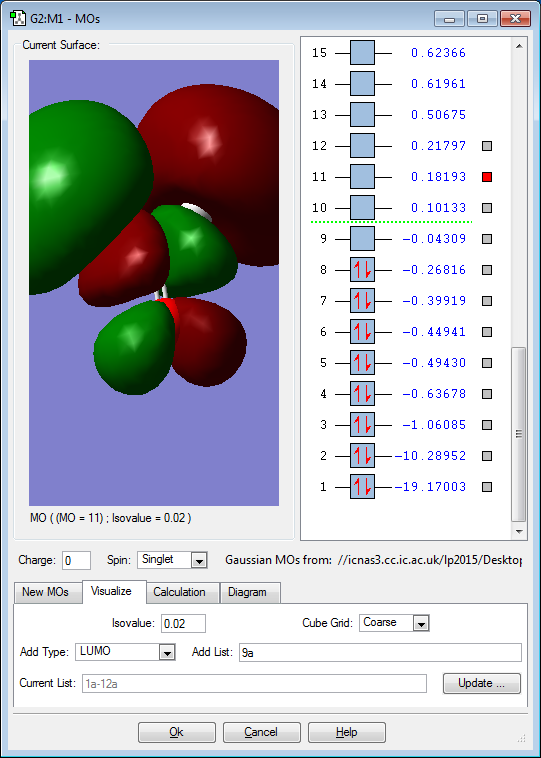
5 Chosen MO Diagrams of H2CO
The 2s orbitals of the atoms contribute to the above MO. It is a bonding occupied MO, deep in energy. As electron pairs are occupying the bonding MO, it stabilises the bonding within the molecule. However, its stablising effect is cancelled out by the destabilisation effect of the occupied bonding MO resulting from the corresponding 2s orbitals of the atoms.
The 2s orbitals of the atoms contribute to the above MO. It is an anti-bonding occupied MO, deep in energy. As electron pairs are occupying the anti-bonding MO, it destabilises the bonding within the molecule. However, its destablising effect is cancelled out by the stabilisation effect of the occupied bonding MO resulting from the corresponding 2s orbitals of the atoms.
The 2p orbitals of the atoms contribute to the above MO. It is a bonding occupied MO, deep in energy. As electron pairs are occupying the bonding MO, it stabilises the bonding within the molecule.
The 2p orbitals of the atoms contribute to the above MO. It is an anti-bonding occupied HOMO.As electron pairs are occupying the bonding MO, it destabilises the bonding within the molecule. However, its destablising effect is cancelled out by the stabilisation effect of the occupied bonding MO resulting from the corresponding 2p orbitals of the atoms.
The 2p orbitals of the atoms contribute to the above MO. It is a bonding unoccupied LUMO. As electron pairs are not occupying the bonding MO, it has no effect on the bonding within the molecule.
The 3s orbitals of the atoms contribute to the above MO. It is a bonding unoccupied MO, high in energy. As electron pairs are not occupying the bonding MO, it has no effect on the bonding within the molecule.
SiH4 molecule
Calculation Method: RB3LYP
Basis Set: 6-31G(d.p)
Final Energy E(RB3LYP): -291.88802760 a.u.
RMS Gradient Norm: 0.00000002 a.u.
Point Group: TD
Si-H bond distance = 1.48485 ångström
H-Si-H bond angle = 109.471 °
test molecule |
The optimisation file is liked to here
Item Value Threshold Converged?
Maximum Force 0.000000 0.000450 YES
RMS Force 0.000000 0.000300 YES
Maximum Displacement 0.000000 0.001800 YES
RMS Displacement 0.000000 0.001200 YES
Predicted change in Energy=-2.451080D-14
Optimization completed.
-- Stationary point found.
----------------------------
! Optimized Parameters !
! (Angstroms and Degrees) !
-------------------------- --------------------------
! Name Definition Value Derivative Info. !
--------------------------------------------------------------------------------
! R1 R(1,2) 1.4849 -DE/DX = 0.0 !
! R2 R(1,3) 1.4849 -DE/DX = 0.0 !
! R3 R(1,4) 1.4849 -DE/DX = 0.0 !
! R4 R(1,5) 1.4849 -DE/DX = 0.0 !
! A1 A(2,1,3) 109.4712 -DE/DX = 0.0 !
! A2 A(2,1,4) 109.4712 -DE/DX = 0.0 !
! A3 A(2,1,5) 109.4712 -DE/DX = 0.0 !
! A4 A(3,1,4) 109.4712 -DE/DX = 0.0 !
! A5 A(3,1,5) 109.4712 -DE/DX = 0.0 !
! A6 A(4,1,5) 109.4712 -DE/DX = 0.0 !
! D1 D(2,1,4,3) -120.0 -DE/DX = 0.0 !
! D2 D(2,1,5,3) 120.0 -DE/DX = 0.0 !
! D3 D(2,1,5,4) -120.0 -DE/DX = 0.0 !
! D4 D(3,1,5,4) 120.0 -DE/DX = 0.0 !
--------------------------------------------------------------------------------
Vibration Modes
Number of Vibration Modes: 9 Modes
Degenerate Modes: Modes 1, 2 & 3; Modes 4 & 5; Modes 7, 8 & 9
Number of Bands Expected in Experimental Spectrum of Gaseous SiH4: 4 Bands
Charge Distribution of Atoms in SiH4
Charge of Silicon Atom: 0.336
Charge of Hydrogen Atoms: -0.084
As the valence electrons of Silicon experiences greater shielding, the effective nuclear force acting on its valence electrons are weak, hence its valence electrons are pulled away from itself towards the respective Hydrogen atoms, resulting in its positive charge. The valence electrons of Hydrogen atoms experiences lesser shielding, hence it is able to pull electrons to itself, resulting in its slightly negative charge.