Rep:Mod:lp0190 module3
Module 3 - Transition States and reactivity
Introduction
Molecular Mechanics and Force Field methods (used in Module 1) can’t be used to find the energy of Transition States; as they don’t describe the breaking and making of bonds and the changes in electron distribution. Therefore, molecular orbital methods have to be used. In this module transition states will be located using the shape of potential energy surface, this will show how transition structures look like, their reaction paths and activation energies.
In particular, molecular orbitals methods will be used to study the Cope rearrangement and the Diels Alder Cycloaddition.
The Cope Rearrangement
The Cope rearrangement is an organic reaction involving a [3,3]-sigmatropic rearrangement of 1,5 dienes. The reaction scheme is reported below.
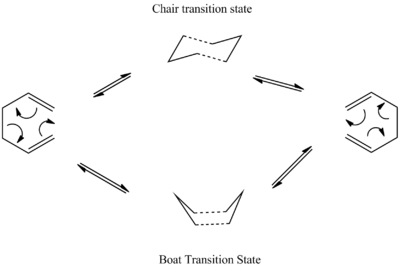
The reaction proceeds in a concerted fashion via either a Chair or a Boat Transition state. Activation energies and enthalpies will be calculated for both, but in order to do that the reactants and products have first to be optimized.
Optimization of Reactants and Products
There are 10 different conformations for 1,5-hexadiene, namely 4 antiperiplanar and 6 gauche. Two conformations of each were drawn on Gaussview and optimized at the HF/3-21G level. The obtained structures were named in the same way as indicated in appendix one; their point group and their energies are reported below in Table 1.
| Structure | Picture | 3D | Point Group | Energy/ kJmol-1 | DOI of optimization |
| Anti1 | 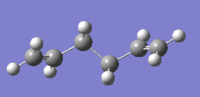 |
C2 | -231.69260 | DOI:10042/to-11134 | |
| Anti2 | 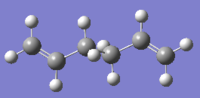 |
Ci | -231.69254 | DOI:10042/to-11137 | |
| Gauche3 | 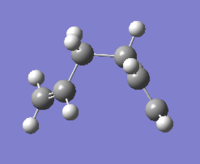 |
C1 | -231.69266 | DOI:10042/to-11135 | |
| Gauche4 |  |
C2 | -231.69153 | DOI:10042/to-11136 |
From table 1 it can be seen that firstly the structure, point group and energy of the identified conformers is in very good agreement to the values reported in Appendix 1 and secondly that the preferred (i.e. lowest in energy) conformation of 1,5-hexadiene is Gauche3.
Alkanes are often found to be more stable in the anti-periplanar orientation because this orientation tends to maximize the amount of hyperconjugation (i.e. the number of bonding and antibonding orbital interactions in a molecule). In addition, the antiperiplanar conformation ensures that bond repulsions are at a minimum. However, 1,5-hexadiene has two double bonds which have to be taken into account. In gauche3 the double bonds are quite close to each other, thus the unexpected stability of Gauche3 is due to secondary orbital interactions between the two double bonds, which lowers the overall energy of the molecule.
The Anti2 conformation was then optimized at the B3LYP/6-31G* level DOI:10042/to-11348 . The two energies obtained can't be compared as they are calculated using different methods; however, a comparison of the obtained geometry can be made.
| Parameter | HF/3G-21 | B3LYP/6-31G* | Lit.[1] |
| C3-C4 /Å | 1.553 | 1.548 | 1.536 |
| C2-C3/Å | 1.509 | 1.504 | 1.507 |
| C1=C2/Å | 1.316 | 1.334 | 1.341 |
| (C-H)mean/Å | 1.075 | 1.094 | 1.108 |
| C2-C3-C4/° | 111.4 | 112.7 | 111 |
| C1=C2-C3/° | 124.8 | 125.3 | 122.5 |
| C2=C1-H/° | 121.8 | 121.7 | 120.4 |
| C3-C2-H/° | 115.5 | 115.7 | 118.4 |
| H-C3-H/° | 107.7 | 106.7 | 107.1 |
| C2-C3-C4-C5/° | 180 | 180 | -178.3 |
| C1=C2-C3-C4/° | 114.7 | 118.5 | 116 |
| C3-C4-C5=C6/° | 114.7 | 118.5 | 116 |
| Energy/a.u. | -231.69254 | -234.61170 |
From the table it can be seen that the geometry was not strongly affected when changing between the two levels of theory, as they are in good agreement with each other and very close to literature values.
The only way to make sure a global minimum was obtained in the optimization is to perform a frequency analysis DOI:10042/to-11349 and check if no negative frequencies are present. If an imaginary negative frequency is present then this highlights that a transition state rather than a minimum was obtained. The computed IR spectrum of Anti2 1,5 hexadiene is reported below.
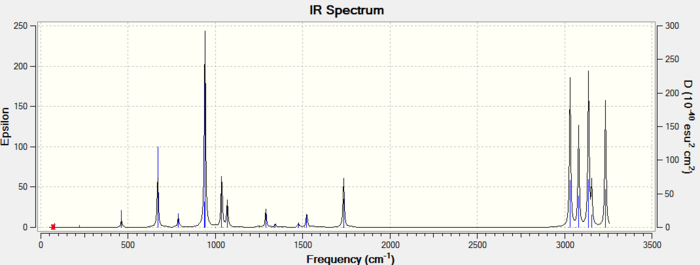
The frequencies are all real, thus highlighting an energy minimum was in fact reached during the optimization step. By opening the .log file further information can be found which will later be used to calculate the activation energies.
Sum of electronic and zero-point Energies= -234.469212 Sum of electronic and thermal Energies= -234.461856 Sum of electronic and thermal Enthalpies= -234.460912 Sum of electronic and thermal Free Energies= -234.500821
Optimization of Transition States
Chair Optimization
A CH2CHCH2 fragment was drawn and optimized using the HF/3-21G level of theory DOI:10042/to-11360 . The optimized structure was then pasted twice on a new Guassian window and the distance between the two terminal ends of the allyl fragments was set to 2.2A. The product was made to look as similar as the presumed chair transition state as possible. The guessed structure was then optimized using two different methods: the Berny method and the freeze coordinate method.
Transition State Optimization: Berny Method
The first method was to run to run an Optimization+Frequency job on the guessed structure, optimizing to a Berny Transition State and calculating force constants only once DOI:10042/to-11354 . The output of the optimization is reported below. The imaginary (negative) frequency at 818 cm-1 which proves that a transition state was in fact obtained is also reported.

The animation clearly highlights that the imaginary frequency corresponds to the Cope rearrangement as the motion corresponds to the bond forming and bond breaking.
The Freeze Coordinate method
The previous method only works if the guessed structure is close to the exact structure. If the two are instead different the approach might not work. A better method is to therefore freeze the reaction coordinate and optimize the rest of the molecule. Once the molecule is optimized the reaction coordinate can be unfrozen and the transition state can be minimized again.
The Redundant Coordinate Editor was used to Freeze the distance between the two two terminal allyl carbons (the length was set to 2.2A). An HF/3-21G optimization to a minimum was then carried out DOI:10042/to-11358 . From this structure the frozen bonds were then optimized, by running an Opt+freq job to a Berny Transition State, after switching the selected bonds from Freeze Coordinate to Derivative DOI:10042/to-11359 . The imaginary frequency was found to be at 818 cm-1 , in good agreement with the previous method.
| Parameter | Berny | Frozen coordinate |
| Energy/a.u | -231.61932 | -231.61932 |
| Imaginary Frequency/cm-1 | -818 | -818 |
| Separation of two allyl groups/Å | 2.02 | 2.02 |
| C-C/Å | 1.39 | 1.39 |
| C-C-C/° | 121 | 121 |
The table clearly shows that both methods work very well in this case as they both gave back exactly the same results.
Boat Optimization
To optimize the Boat transition structure the QST2 method was used. In this method the reactants and the products for a reaction are specified and the calculation is used to interpolate between the two structures and find the transition state between them.
The optimized (Anti2) 1,5- hexadiene was pasted into two windows on Gaussview. The numbering on both structures was changed, to make sure the numbering on the product was consisted with the rearrangement. A picture of this is reported below.
The QST2 calculation was run on Gaussian as an Opt+Freq and the structure was optimized to a transition state TS(QST2) DOI:10042/to-11419 . The structure produced by this calculation is reported below.
This structure is clearly wrong, as it looks the same as a Chair transition structure (just slightly more dissociated). The allyl fragment was just linearly translated as the software wasn't able to consider a rotation about the central bonds.
Therefore, in order to obtain a Boat Transition Structure using this method, the geometry of the reactant and product has to be changed. The geometry used is reported in the picture below.
The QST2 calculation was then set up in the same way as before but this time the calculation converged to produce the following transition state DOI:10042/to-11420 .
As expected from a transition state, only one imaginary frequency is observed at 840cm-1, reported below.
| Parameter | QST2 Boat TS |
| Energy/a.u | -231.60280237 |
| Imaginary Frequency/cm-1 | -840 |
| Separation of two allyl groups/Å | 2.14 |
| C-C/Å | 1.38 |
| C-C-C/° | 122 |
By comparing the energy in table 4 with the one in table 3 it can be seen that the boat is 10.4 Kcalmol-1 higher in energy than the chair transition state. In addition the separation of the two allyl groups is greater in the boat TS, thus proving that the chair conformation is the preferred route.
IRC
The Intrinsic Reaction Coordinate (IRC) is a method implemented in Gaussian which allows to follow the minimum energy path from a transition structure down to its minimum on a potential energy curve. It works by taking small geometry steps in the direction where the gradient of the energy surface is steepest.
IRC Chair
The first IRC calculation for the chair TS was carried out from the Berny optimized structure. The reaction coordinate was computed only in the forward direction, as it is symmetrical, the force constants were only calculated once and the number of points on the IRC was set to 50. DOI:10042/to-11421
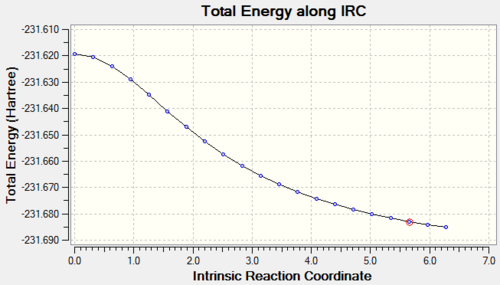
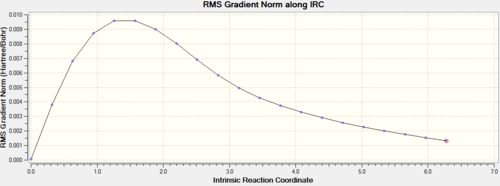 |
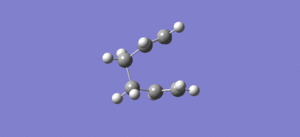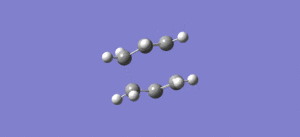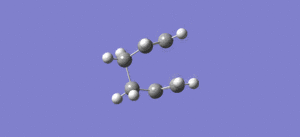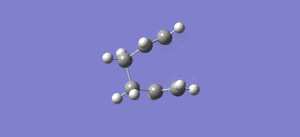 |
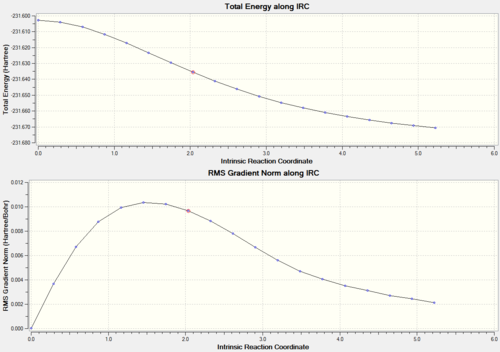
After going through 21 intermediate geometries, it can be seen from the energy gradient graphs that the reaction didn't reach a minimum, as since the gradient didn't reach 0.
There are three different options that can be taken in order to identify the minimum. The first option is to minimize the last structure given by the IRC, the second option is to restart the IRC and specify a larger number of points until it reaches a minimum, while the third approach is to redo the IRC specifying to compute the force constants at every step. Only the first and the third option were carried forward, because, the IRC stopped after 21 intermediate structures, when the number of points was set to 50, so there's no reason to increase the number of computed points. The two methods were then compared.
Method one: optimization of last IRC structure
The last structure obtained by the previous IRC is reported in figure 13. The structure was optimized to a minimum using HF/3-21G> The optimised structure is shown in figure 14 DOI:10042/to-11422 .
 |
 |
Method 2: Recalculating force constants at every step
The same calculation carried out in the previous IRC was set out, only this time it was specified to calculate force constants at every step. DOI:10042/to-11423
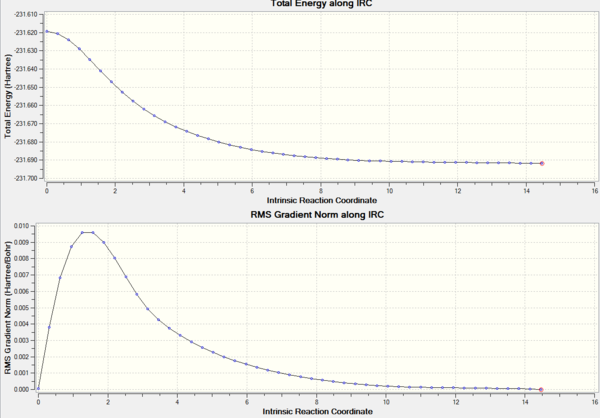
 |
A comparison of the structure and the energies obtained using the two methods is reported in the following table.
| Parameter | IRC original | IRC+Optimization | IRC method 2 |
| Energy/a.u | -231.6851424 | -231.691667 | -231.6916643 |
| Gradient/a.u | 0.00133718 | 0.00000596 | 0.00001161 |
| Bond Broken/Å | 3.07 | 4.39 | 4.36 |
| Bond Formed/Å | 1.57 | 1.55 | 1.55 |
| C-C/Å | 1.5 | 1.5 | 1.5 |
| C-C-C/° | 124 | 125 | 125 |
The table shows that both methods: the optimization and the second IRC calculation give very similar results, thus confirming that both methods are useful and work in this case.
IRC Boat
The same IRC calculation carried out for the chair TS was repeated for the Boat TS DOI:10042/to-11424 .
 |
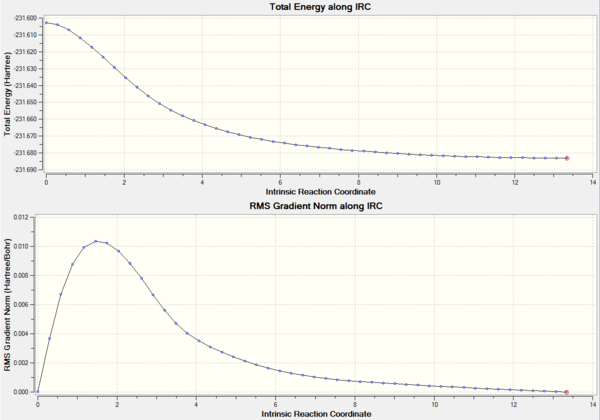
As with the chair conformation, it can be seen from the graph that the calculation didn't converge when force constants were only calculated once, as a result the IRC was repeated calculating the force constants at every step. This time only this method was used as it is the most accurate out of the previously mentioned 3. DOI:10042/to-11425
 |
Information about the Boat TS final IRC caluclation is reported in the table below.
| Parameter | IRC original | IRC method 2 |
| Energy/a.u | -231.6706934 | -231.6830253 |
| Gradient/a.u | 0.00212444 | 0.00000593 |
| Bond Broken/Å | 2.95 | 4.33 |
| Bond Formed/Å | 1.6 | 1.58 |
| C-C/Å | 1.31 | 1.31 |
| C-C/Å | 1.51 | 1.51 |
| C-C-C/° | 124 | 124 |
Activation Energies
Activation energies were calculated by carrying out opt+freq calculation of the Chair and Boat Transition states and the Anti2 reactant. The opt+freq was calculated both at the HF/3-21G and at the B3LYP/6-31G* level of theory DOI:10042/to-11427 ,DOI:10042/to-11429 . The energies and the thermodynamic data for the 3 structures at the 2 levels of accuracy is reported in the table below.
| HF/3-21G | B3LYP/6-31G* | |||||
|---|---|---|---|---|---|---|
| Electronic energy | Sum of electronic and zero-point energies | Sum of electronic and thermal energies | Electronic energy | Sum of electronic and zero-point energies | Sum of electronic and thermal energies | |
| at 0 K | at 298.15 K | at 0 K | at 298.15 K | |||
| Chair TS | -231.619322 | -231.466696 | -231.461337 | -234.543093 | -234.414931 | -234.409010 |
| Boat TS | -231.602802 | -231.450925 | -231.445295 | -234.543093 | -234.402341 | -234.396006 |
| Reactant (anti2) | -231.692535 | -231.539540 | -231.532566 | -234.611703 | -234.469212 | -234.461856 |
Using the above information and taking 1 Hartree = 627.509 kcal/mol the activation energies for the two transition states can be calculated.
| HF/3-21G | HF/3-21G | B3LYP/6-31G* | B3LYP/6-31G* | Expt. | |
| at 0 K | at 298.15 K | at 0 K | at 298.15 K | at 0 K | |
| ΔE (Chair) | 45.71 | 44.70 | 34.06 | 33.16 | 33.5 ± 0.5 |
| ΔE (Boat) | 55.60 | 54.76 | 41.96 | 41.32 | 44.7 ± 2.0 |
The table clearly shows the importance of the accuracy of the method used when calculating activation energies. The energies calculated using the B3LYP/6-31G* method are much closer to the experimental value than the ones calculated using HF/3-21G. In addition, from the table it can easily be seen how the activation energy is lower for the chair TS, thus proving that the Cope rearrangement goes through a chair TS.
Diels-Alder Cycloaddition
The Diels-Alder Cycloaddition is an example of a pericyclic reaction, in which the п orbitals of the dienophile are used to form new σ with the п orbitals of the diene. In general the HOMO/LUMO of one fragment interacts with the HOMO/LUMO of the other reactant to form two new bonding and anti-bonding MOs. If the HOMO of one reactant can interact with the LUMO of the other, the reaction is allowed, while if the HOMO and LUMO have different symmetry properties no overlap is possible and the reaction is forbidden.
Optimization Of Reactants
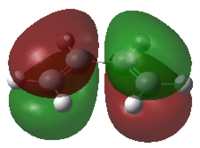
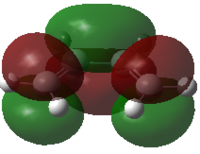
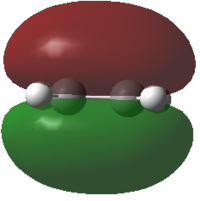
Butadiene and ethene were optimized at the semi empirical AM1 method. The HOMO and LUMO were calculated and are reported below.
 |
 |
 |
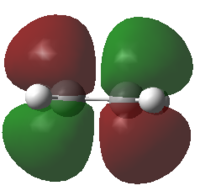 |
From the pictures it can be seen that the Butadiene HOMO is antisymmetric, while its LUMO is symmetric. The Ethene HOMO is symmetric while its LUMO is antisymmetric.
Therefore the reactant's HOMO/LUMO are of the correct geometry and the reaction is allowed. The Transition State will now be optimized in order to see which HOMO interacts with which LUMO.
Transition state optimization
The Transition state was made by selecting a bicyclic system on Gaussview and removing the -Ch2-Ch2- bridge. This ensured the structure was in an envelope position. Another 2 bonds were deleted in order to separate the two fragments (but-2-ene and ethene); the distance was specified to be 2.2Å. An opt+freq job was run optimizing the molecule to a TS Berny at the AM1 level of theory. The optimized strucutre is reported below. to-11546
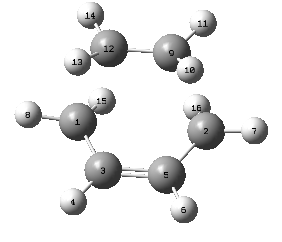
| Parameter | Value |
| Energy/a.u | 0.11165466 |
| Gradient/a.u | 0.00001548 |
| Fragment separation/Å | 2.19 |
| C1-C3/Å | 1.38 |
| C3=C5/Å | 1.4 |
| C5-C2/Å | 1.38 |
| C12-C19/Å | 1.38 |
The bond lengths are in good agreement with the idea that pericyclic reaction progress via an aromatic delocalised intermediate as they are smaller than single C-C bond lengths(on average 1.54Å) and bigger than C=C bond lengths (on average 1.54Å).
The distance between the two fragments is 2.19Å which is bigger than a single C-C bond but it still lies within twice the Carbon Van der-Waals radius, which is 3.4Å. This highlights that there is a bonding interaction between the two fragments.
By optimising to a Transition state one negative frequency was obtained at 956 cm-1, highlighting the fact that a transition state was reached. The animation clearly shows that the frequency represents the concerted formation of the new sigma bonds. The lowest real frequency occurs at 147 cm-1 and shows the asynchronous twisting of the two fragments. This is the weakest vibration since the bonds between the two fragments are the weakest, as they are not fully made yet.
 |
 |
From the optimized file the Transition State's HOMO and LUMO can be identified.
 |
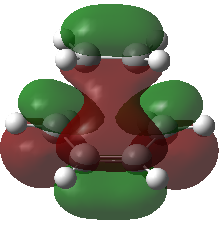 |
It can clearly be seen that the Transition State HOMO was made out of the HOMO of Butadiene and the LUMO of ethene, thus since both of them are antisymmetric the Transition State HOMO will be antisymmetric. The Transition state LUMO is instead symmetric, as it is made by the symmetric Butadiene LUMO and the symmetric Ethene HOMO.
Cyclohexa-1,3-diene reaction with Maleic Anhydride
Cyclohexa-1,3_diene reacts with maleic anhydride to give primarily the endo product. This is known as the endo rule; under kinetic conditions a reaction will preferentially give out the endo product as this is produced faster (i.e. has the lowest activation energy). The reason why the endo product is produced at a faster rate is that in the endo orientation the product is stabilized through secondary orbital overlap, which are not present in the exo product. In this module the transition state of this reaction will be studied.
Optimization Transition State
The endo and exo transition states were optimized using the Frozen coordinate method (distances frozen to 2.2Å), under the semi-empirical AM1 level of optimization. DOI:10042/to-11544 DOI:10042/to-11545
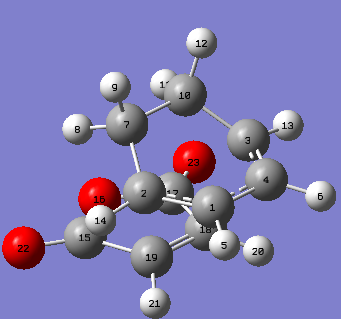 |
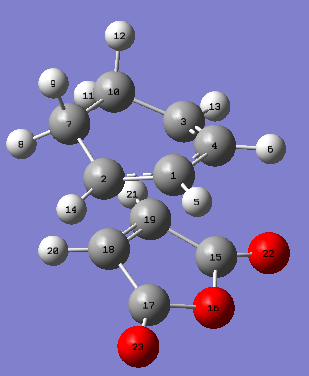 |
| Parameter | Endo | Parameter | Exo |
| Energy/a.u | -0.05150448 | Energy/a.u | -0.05041953 |
| Gradient/a.u | 0.00006851 | Gradient/a.u | 0.00002923 |
| Fragment separation/ | 2.16 | Fragment separation/ | 2.17 |
| C15-C4/C17-C1 | 2.89 | C7-C15/C17-C10 | 2.94 |
| C18=C19 | 1.41 | C18=C19 | 1.41 |
| C1=C4 | 1.4 | C1=C4 | 1.4 |
| C1-C2/C4-C3 | 1.39 | C1-C2/C4-C3 | 1.39 |
From the table above it can be seen that the Endo TS is lower in energy by 2.84 kJmol-1 compared to the Exo Ts, thus confirming the theory that the Endo TS has the lowest activation energy, due to the secondary orbital interaction and the lower steric hindrance between the anhydride group and the carbons on the second fragment.
They both showed an imaginary vibration which is reported below.
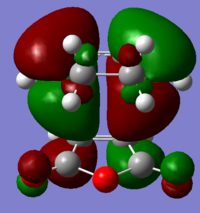
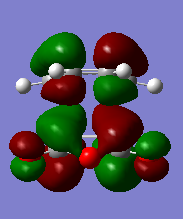
The HOMO and LUMO molecular orbitals of the two transition states are also reported below.
| Endo | Exo |
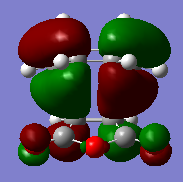 |
 |
 |
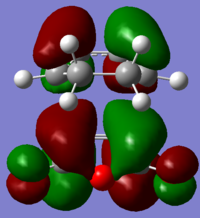 |
The orbitals are all asymmetric, there should be second orbital interaction between teh maleic anhydride and the CH=CH, which stabilizes the endo TS more than the exo, however this is not present (or it is difficult to see here).
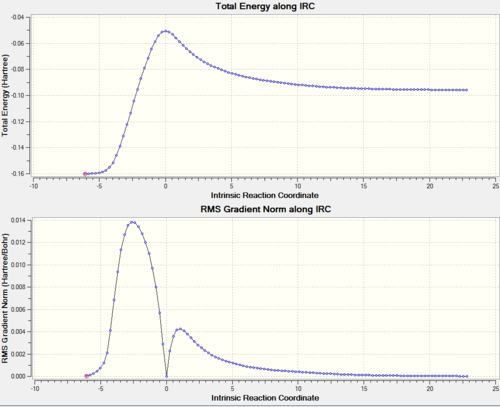
An IRC calculation was also carried out for the two transition states. DOI:10042/to-11543 DOI:10042/to-11547 The IRC was done by computing 100 points, lloking at both directions of the reaction coordinate and calculating the force constant at every step.
 |
 |
Conclusion
The module put forward the usefulness of molecular orbital methods in visualizing Transition States. Apart from just being able to see the structure of the transition state, the method makes it possible to obtain the activation energies for different transition states. The obtained results are very similar to the ones obtained experimentally, thus making computational techniques very important, in the prediction of which energy path will be taken and what will be produced during a certain synthesis
References
- ↑ G. Schultz, I. Hrgittai, J. Mol. Struct., 1995, 346,63-69
