Rep:Mod:lnwreport
Transiton States and Reactivity: Wiki Report.
Introduction
A pericyclic reaction is a process in which the transition structure of a reaction is cyclic and usually proceeds in a concerted fashion. In order for a reaction to be thermodynamically allowed it must adhere to the Woodward Hoffman rules. The Woodward-Hoffman Rules state that a reaction proceeds when the sum of (4q +2)s + (4r)a is odd, where are q and r are integers and the total number of suprafacial and antarafacial components correspond to the number of π electrons in the system.
The transition states of two pericyclic reactions, the Cope rearrangement and a Diels-Alder cycloaddition, were investigated.
The Cope rearrangement is a [3,3] sigmatropic rearrangement involving the formation and breaking of bonds at either end of a conjugated π system. The boat transition structure is known to be higher in energy, around 5-6 kcal mol-1 [1] and is theorised to proceed synchronously.
The Diels Alder reaction is a [4+2] peri cyclic and involves the formation of two sigma bonds on either side of two conjugated systems. The reaction between ethylene and cis-butadiene and the reaction between maleic anhydride and cyclohexane-1,3-diene. The latter gives a mixture of products with the major product being the kinetic not thermodynamic product. This is to do with favourable interactions in the transition state which lowers the activation energy of the system.
The transition structures were optimised and investigated using Gaussian 09W and visualised using Gaussview 5.0. These two systems were investigated using a variety of methods. In the Cope rearrangement, the transition structures were optimised using a variety of methods at two levels of theory (HF/3-21G and B3LYP/6-31G*):
- Optimisation using the Berny algorithm.
- Optimisation by the QST2 method, where the reactant and products are built and Gaussian interpolates between the two to find a transition structure.
- Optimisation using the Frozen coordinate method, where the carbon distances where the bonds are formed in the reaction are fixed to a known distance and the structure and the these frozen bonds are optimised to a transition state separately.
For the Diels Alder reaction the transition states were optimised at two levels, the semi-empirical AM1 level and the B3LYP/6-31G* level. The transition states were optimised using the Berny algorithm.
The calculated structure was found to be a transition state using various methods, namely running IRC calculations and monitoring the frequencies of the transition structures. IRCs, or Intrinsic Reaction Coordinates, follow the structure down the slope of steepest gradient in the forward and backwards direction in order to determine whether the structure was truly at a maximum. The number of imaginary (less that 0 cm-1) frequencies corresponds to the order of the saddle point at which the structure lies on the potential energy surface. Therefore the transition structures will have one negative frequency as they sit at 1st order saddle points.
Nf710 (talk) 17:32, 18 November 2015 (UTC) Nice introduction however you could have gone into more detail about the various levels of theory used and how HF and DFT methods are different. Also you could have explained how the imaginary frequencies are calculated
Cope Rearrangement Tutorial
Optimisation of Reactants
Three different conformers of 1,5-hexadiene were optimised using Hartree Fock optimisation at the 3-21G basis set.
| Conformer | Structure | Point Group | Energy /au | Log file | |
|---|---|---|---|---|---|
| 1 | Anti 1 |  |
C2 | -231.69260 | x |
| 2 | Anti 2 |  |
Ci | -231.69253 | x |
| 3 | Gauche 1 |  |
C1 | -231.68916 | x |
| 4 | Gauche 2 |  |
C1 | -231.69266 | x |
Molecule 1 was built in an anti conformation, with the two ethylene groups antiperiplanar when viewed as a Newman projection. After optimisation, the molecule was found to have C2 symmetry without any relaxation of the tolerance.
Molecule 2 was another anti conformation of 1,5-hexadiene. After optimisation it had a point group of Ci and an energy of -231.69253 Ha. The energy calculated was very similar to the calculated energy found in literature, which was given as -231.69254 Ha.[2]
Molecule 3 was drawn with a gauche relationship between the two ethylene groups. Sterically, this molecule was more hindered so it was expected that this gauche conformer would have a higher energy than molecule 1. After optimisation, this was shown, although the energy difference was very slight.
It would be expected that the less hindered a molecule, the lower its energy. The further away from each other the substituents are the less steric clash and torsional strain. However, for 1,5-hexadiene this is not the case. This is due to favourable electronic interactions between the two ethylene groups that only occur in the gauche confirmation, where the two groups are close enough to interact. This lowest energy conformer is Molecule 4. Molecule 4 had a point group of C1. The energy of the molecule after optimisation is lower than that of 1, 2 and 3, but only very slightly. This very slight change in energy implies that the electronic interactions aren't very strong.
Nf710 (talk) 17:28, 18 November 2015 (UTC) You could have proved why the gauche conformer has the lowest conformation if you had looked at the orbitals in the .chk file as they would have clearly shown the secondary orbital interactions
Molecule 2 was then re-optimised using DFT at the B3LYP/6-31G* level. After optimisation the energy was calculated as -234.61171 Ha. The bond angle between the the two central carbons and the adjacent carbon increased from 111.3° to 112.6° as well as a slight increase between the two double-bonded carbons and the adjacent central carbon, from 124.8° to 125.3°. The length of the bond between the central two carbons increased from 1.548 Å to 1.553 Å. There was also an increase in the length of the C-C double bond from 1.316 Å to 1.334 Å.
However, these energies calculated in the optimisation process do not take into account certain physical quantities so are not comparable with experimental data. In order to compare these virtually modeled molecules with real life experiment, a frequency calculation must be run at the same basis set.
Nf710 (talk) 17:38, 18 November 2015 (UTC) I Dont really know what you are trying to say here. You have a done a fairly good analysis of the geometries, no dihedrals though, and you also forgot to look at the thermochemistry.
A frequency calculation was run on the re-optimised Ci anti conformer of 1,5-hexadiene. No negative frequencies were returned as seen in Fig. 2, so the structure was at a potential energy minimum.
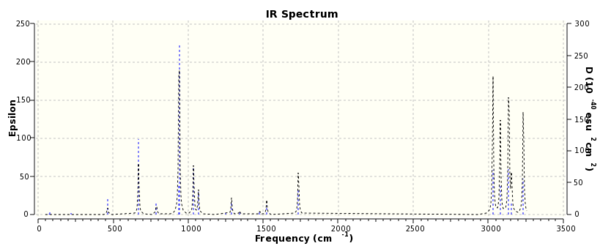
Optimisation of Chair and Boat Transition States.
Chair Structure
A C3H5 allyl fragment was optimised at the HF/3-21G level. This optimised structure was copied and then the two fragments were positioned until they were in an approximate Chair structure with the terminal carbons approximately 2.2 Å apart.
An opt+freq calculation for this approximate structure was then run with Hartree-Fock and a 3-21G basis set, to find the transition state (Berny). The calculation resulted in one negative frequency at -817.95 cm-1, which corresponds to the Cope rearrangement. The bond lengths between terminal carbons were found to be 2.0200 Å and 2.0199 Å.
The same initial chair structure was then optimised using the frozen coordinate method. The bond distance between the two terminal carbons was kept constant during optimisation. The result of this calculation was then optimised to find a transition state, this time instead of keeping the terminal carbon distances frozen, derivative was chosen instead. The bond lengths of the terminal carbons using this method were determined to be 2.0207 Å and 2.0208 Å. One negative frequency was found at 817.88 cm-1.
The terminal carbon distances using both methods were found to be similar, as was the frequency of the vibration corresponding to the reaction path. This indicates that both structures are very similar. The vibration appears to be synchronous, with the formation and breaking of the bond happening simultaneously.
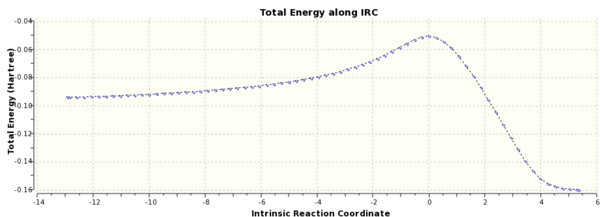
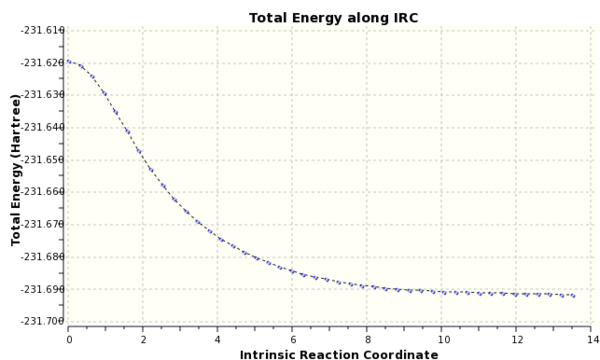
A IRC calculation was run for the chair conformer due to the symmetry of the system it was only run in the forward direction and force constants were calculated at every step.The final structure was a gauche conformer, see Fig. 3. From Fig. 4, it can be seen that the reaction reached a minimum.
Nf710 (talk) 18:39, 18 November 2015 (UTC) Correct frequencies but it would have been good if you could have shown your understanding of why they imaginary from the quantum harmonic oscilator and the second derivative of the PES (force constant)
Nf710 (talk) 18:42, 18 November 2015 (UTC) you could have figured out the conformer it connects by looking at the energies
Boat Structure
The QST2 method was used to determine the transition structure of the Boat configuration. The QST2 method works by interpolating between an initial and final structure to find an intermediate transition structure provided the numbering system in the two structures remains the same. The calculation completed, although according to the experiment's wiki it was meant to fail. The log file can be found here. But the geometry of this calculation was not correct for a boat transition structure, and looked closer to a chair structure.
The geometry of the initial and final structures was modified by rotation about the central C-C bond, and a decrease in the inside C-C-C angles, making it closer to the transition structure. This was re-run under the same basis set and the calculation completed. This time the structure generated was the correct shape and there was one negative frequency at -840.22 cm-1, Fig.5, which seemed to correspond to the Cope Rearrangement.
Figure 5. Imaginary vibration of Boat Transition Structure. |
Reoptimisation of Chair and Boat structures.
The chair and boat transition structures were both then reoptimised using the B3LYP/6-31G* level. In comparison with optimisation at the HF/3-21G level, there was little difference between the structures (see Fig.6 below), however there was a difference in the energies calculated.
| HF/3-21G | B3LYP/6-31G* | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Geometry | E /Ha | ΔE /Kcal mol-1 | Geometry | E /Ha | ΔE /Kcal mol-1 | |||||
| at 298 K | at 0 K | at 289 K | at 0 K | at 298 K | at 0 K | at 289 K | at 0 K | |||
| Chair |  |
-231.46134 | -231.46670 | 44.70 | 45.71 |  |
-234.40898 | -234.414910 | 33.19 | 34.08 |
| Boat |  |
-231.44530 | -231.45093 | 54.76 | 55.60 |  |
-234.43960 | -234.402342 | 41.98 | 41.33 |
| Reactant | |
-231.53257 | -231.53954 | N/A | N/A |  |
-234.46187 | -234.46922 | N/A | N/A |
At both levels of optimisation, the energy of activation of the chair conformer is lower, as this is a more preferred orientation due to less steric clash. Using the experimental values obtained from the wiki script [2], the activation energy 33.5 ± 0.5 kcal mol-1 of the chair at 0K and 44.7 ± 2.0 kcal mol-1 of the boat, the B3LYP/6-31G* is much closer to experimental values than HF/3-21G optimisation. This suggests that B3LYP/6-31G* is a more accurate representation of the actual molecule.
Nf710 (talk) 18:59, 18 November 2015 (UTC) Your energies are correct and you have come to the conclusion that smaller basis sets are good at getting the geom correct but the energies are need to be calculated by higher ones. You haven't shown much understanding of the theory though with this experiment. however you have done everything else that has been asked of you.
The Diels Alder Cycloaddition
Reaction of cis-Butadiene and Ethylene
Cis-butadiene was optimised at using the semi-empirical AM1 level in order to visualise the HOMO and LUMO. The log file can be accessed here.
| MO | Surface | Symmetry with respect to perpendicular reflection plane |
|---|---|---|
| HOMO |  |
|
| LUMO |  |
The transition structure of the Diels Alder reaction was then drawn, using a cis-butadiene fragment and an ethylene fragment, with the terminal carbons around 2.12 Å apart.
This transition state was optimised using the semi-empirical AM1 method as before, but this time was optimised to a transition state using the Berny algorithm, with calculation of the force constant once.
After optimisation of the transition state, the distance between the terminal carbons on both groups was 2.119 Å. There was also a negative frequency at -956.27 cm-1 present in the vibration table, which corresponded with the Diels Alder Reaction, as seen in Fig. 8. The vibration shows that the formation of the two σ sigma bonds is synchronous, unlike the smallest positive vibration of the same optimisation which displays an asynchronous vibration. This is expected for the reaction between ethylene and cis-butadiene[3].
("Asynchronous" refers to bond formation. A bond won't form through positive frequency and so this vibration shouldn't be described as asynchronous Tam10 (talk) 13:02, 9 November 2015 (UTC))
Figure 8. Imaginary Vibration of Transition State |
| MO | Surface | Symmetry with respect to perpendicular reflection plane |
|---|---|---|
| HOMO |  |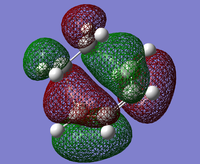
|
| LUMO |  |
The HOMO of this transition state is antisymmetric with respect the perpendicular mirror plane. As only orbitals of the same symmetry can interact this shows that the HOMO is formed from the HOMO of butadiene and the LUMO of ethylene, so this reaction is allowed. And so the LUMO of the transition state was formed from the interaction of the LUMO of butadiene and the HOMO of ethylene.
For carbon-carbon bonds, the average length of an sp3-sp3 bond is 1.54[4] Å and that of an sp2-sp2 double bond is 1.335 Å[4].The van der Waals radius of carbon is given by literature as 1.7 Å[5]. The distance between the two terminal carbons in the transition state structure was 2.119 Å. This distance is larger than the distance between two bonded sp3 carbons but is less than twice the van der Waals radius, which seems to indicate a bond in the process of forming in the transition state.
Diels Alder Reaction of Maleic Anhydride and Cyclohexa-1,3-diene
Cyclohexa-1,3-diene undergoes a facile reaction with maleic anhydride to form a Diels Alder adduct. There are two possible products of this reaction, the exo and the endo product. The exo product would be expected to be the dominant product due to favourable sterics, with the -(C=O)-O-(C=O)- bridge in the favorable equatorial position. Firstly, the reagents were built and optimised at the semi-empirical AM1 level, and then arranged so that they closely resembled the transition states. These guess transition structures were then optimised at the same semi-empirical AM1 level to a transition state using the Berny algorithm.
(I don't understand the 3rd statement above. What "favourable sterics"? And what is the "equatorial position" in this context? Tam10 (talk) 17:21, 10 November 2015 (UTC))
| Geometry | Structure | Energy (kJ mol-1) | Imaginary Frequency (cm-1) | ||
|---|---|---|---|---|---|
| Exo |  |
-132.38 | -812.27 | ||
| Endo |  |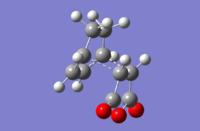
-135.21 | -806.45 |
(What are these energies relative to? A negative relative energy for a transition state is unexpected Tam10 (talk) 17:21, 10 November 2015 (UTC))
The exo transition state is higher in energy than the endo transition state. This indicates that this reaction is actually kinetically controlled, with the kinetic product, the endo-product, being the major product. The endo product is favourable due to electronic interactions between the -(C=O)-O-(C=O)- bridge and the conjugated diene system.
| Exo | Endo | |
|---|---|---|
| Bond |  |
|
| C6-C5 | 2.17032 Å | 2.16234 Å |
| C2-C3 | 2.17041 Å | 2.16238 Å |
| C1-C2 | 1.48977 Å | 1.39304 Å |
| C4-C6 | 1.39439 Å | 1.49054 Å |
| C7-C9 | 2.94519 Å | N/A |
| C8-C10 | 2.94500 Å | N/A |
| C1-C9 | N/A | 2.89230 Å |
| C4-C10 | N/A | 2.89216 Å |
The transition state bond lengths for the endo and exo products are similar, but are slightly smaller for the endo system. This may be due to the electronic interactions which make this product more favourable. The difference in bond lengths between the breaking carbon-carbon double bonds may be indicative of an asynchronous transition state.
The distance between the -(C=O)-O-(C=O)- and the closest -C-C- bridge is larger for the exo product, a clear sign that this transition state is less sterically hindered.
However for the endo to be the preferred product the electronic interactions must be more favourable than the reduction in energy due to less steric hindrance.
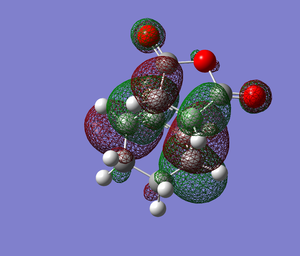
The HOMO of the endo transition state is antisymmetric with respect to the perpendicular mirror plane, as seen in Figure 12. The contribution from the -(C=O)-O-(C=O)- fragment is anti-bonding, and very small. As seen in Figure 13., there is no contribution from the -(C=O)-O-(C=O)- fragment in the exo transition state, so there is no electronic stabilisation in this transition state. There is some debate about the existence of secondary orbital overlap [6], as the distance where the overlap would theoretically be is too large, so no interaction could occur. There is also experimental evidence of reactions where an endo preference would have been expected, that produced an exo major product.
Instead it has been put forward[7] that solvent interactions between the permanent dipoles of diene and dienophile decrease the energy of the reaction, in some cases with preference for the endo transition state. Another theory [6] is to do with electrostatic repulsion between the slightly positively charged hydrogens on the bridges attached to the cyclic ring. This would explain the preference for the endo over exo product, due to steric clashes between the hydrogens attached to sp3 carbons on the bridge and the oxygen groups from the maleic hydride in the exo product. In the endo product the hydrogens closest to the oxygens from the maleic anhydride are sp2 so would not clash with the oxygen groups.
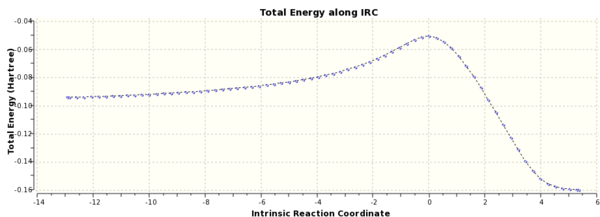
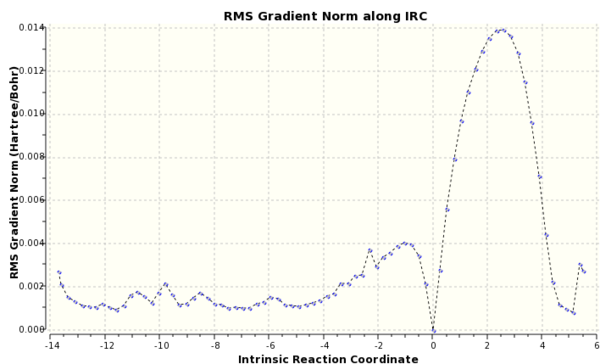
IRC calulations were run at the semi-empirical AM1 level of theory on the endo and exo products, see Appendix. By following the pathway produced from the IRC both in the forwards and backwards direction, it can be seen that a transition state for both the Endo and Exo products were found from the minima that the paths connected.
| Semi-Empirical AM1 | B3LYP/6-31G* | |||||||
|---|---|---|---|---|---|---|---|---|
| E /Ha | ΔE /Kcal mol-1 | E /Ha | ΔE /Kcal mol-1 | |||||
| at 298 K | at 0 K | at 289 K | at 0 K | at 298 K | at 0 K | at 289 K | at 0 K | |
| Endo | 0.143683 | 0.133494 | 66.00 | 65.88 | -612.491836 | -612.50221 | 55.59 | 56.12 |
| Exo | 0.144881 | 0.134881 | 66.75 | 66.75 | -612.48966 | -612.49800 | 58.22 | 58.76 |
| Reactants | 0.038505 | 0.028503 | N/A | N/A | -612.58044 | -612.59164 | N/A | N/A |
From literature[8], the values of the activation energy for this Diels Alder Reaction was found to be 42.235 kcal mol-1 for the endo product and 43.614 kcal mol-1 at 298K. Although neither basis set agrees with the literature value, the B3LYP/6-21G* is slightly closer, indicating that it is a better match to experiment.
As seen in Fig. 14 above, the exo transition state has a slightly higher energy of activation than the endo product. This supports the theory that the reaction is under kinetic control.
Conclusion
The transition states of the Cope Rearrangement were calculated and it was found that the chair conformation was more stable, with lower energies of activation. HF/3-21G and B3LYP/6-31G* were compared and B3LYP/6-31G* was found to better agree with experimentally determined values, so it can be considered a better match for reality. The transition structures of both the chair and boat returned one negative frequency, and its associated vibration corresponded to the Cope Rearrangement. The IRC of the chair structure showed it occurred at a maximum on the Potential Energy Surface.
The transition structure of the reaction between ethylene and cis-butadiene was optimised. One negative frequency was found at -956.27 cm-1, which corresponded to the synchronous formation of the two σ bonds. The transition structures of the reaction between maleic anhydride and cyclohexa-1,3-diene were optimised using the semi-empirical AM1 method. The endo product was shown to have a lower energy of activation despite being more hindered than the exo transition state. This reaction was therefore under kinetic control. The HOMO and LUMO of the transition states were inspected and found to have little stabilisation from the -(C=O)-O-(C=O)- bridge, which is supported by theory, which suggests that the endo-preference displayed by many reactions has little to do with secondary orbital interactions, as is often posed as the reason behind this selectivity. Instead solvent effects and electrostatics of the molecules themselves may in fact exhibit this selectivity preference.
Appendix
Figure 15(a) and 15(b). IRC and RMS Gradient Norm for Exo Diels Alder Product.
Figure 16(a) and 16(b). IRC and RMS Gradient Norm for Endo Product.
References
- ↑ Wiest O., Black K. A., and Houk K. N. (1994) 'Density Functional Theory Isotope Effects and Activation Energies for the Cope and Claisen Rearrangements ', J. Am. Chem. Soc., 116(), pp. 10336-10337 [Online]. Available at: http://pubs.acs.org/doi/pdf/10.1021/ja00101a078 (Accessed: 05 Nov. 2015).
- ↑ 2.0 2.1 WIKI REFERENCE: https://wiki.ch.ic.ac.uk/wiki/index.php?title=Mod:phys3
- ↑ Houk K.N., Lin Y, Brown F.K. Evidence for the Concerted Mechanism of the Diels-Alder Reaction of Butadiene with Ethylene, J. Am. Chem. Soc., 1986 108(3), pp. 554-556 [Online]. DOI: 10.1021/ja00263a059 (Accessed: 05 Nov. 2015).
- ↑ 4.0 4.1 [1] Cite error: Invalid
<ref>tag; name "bond lengths" defined multiple times with different content - ↑ [2] Cite error: Invalid
<ref>tag; name "VdW" defined multiple times with different content - ↑ 6.0 6.1 Fleming I. (2010) Molecular Orbitals and Organic Chemical Reactions. Chichester: John Wiley & Sons, pp. 298-321. Available at: http://jpkc.huanghuai.edu.cn/include/htmleditor/uploadfile/20130309150247611003.pdf (Accessed: 06. Nov 2015).
- ↑ Berson J.A., Hamlet Z., Mueller W.A. Research Article Prev. Article Next Article Table of Contents The Correlation of Solvent Effects on the Stereoselectivities of Diels-Alder Reactions by Means of Linear Free Energy Relationships. A New Empirical Measure of Solvent Polarity', J. Am. Chem. Soc., 1962 84(2), pp. 297–304 [Online]. Available at: http://pubs.acs.org/doi/abs/10.1021/ja00861a033 (Accessed: 6 Nov. 2015).
- ↑ (2015)The Determinants of Endo Exo Selectivity Diels Alder Reactions of Maleic anhydride: A Theoretical Study, Available at: http://www.undergraduatelibrary.org/system/files/3522.pdf (Accessed: 05 Nov. 2015).