Rep:Mod:lmk

Cope rearrangement Tutorial

Cope rearrangement

In this tutorial, the Cope rearrangement reaction will be examined. The reaction is described as a sigmatropic reaction in which one σ bond is broken and one σ bond is made. In this experiment it will be assumed that the reaction proceeds via a concerted mechanism (You don't assume a concerted mechanism, this is in fact one thing that you can get out of the experiment. João (talk) 12:11, 10 February 2015 (UTC)). 1,5-hexadiene can adopt many different conformations, as the result of the rotation of carbon-carbon single bonds. The anti and gauche conformer of the reactant, 1,5 hexadiene, will be optimised using two different levels of theory: HF/3-21G and B3LYP/6-31G* (DFT). From the calculated energies, the gauche conformer is found to be the lowest energy conformation. The reaction mechanism involves two possible transition state structures: a chair and a boat transition structure. The energies of the two structures will be calculated in order to define which is the most likely to occur during the reaction.

1,5-hexadiene Antiperiplanar conformer

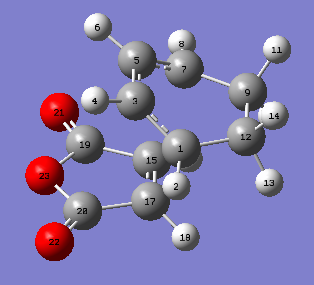
The first part of this tutorial asked to optimize the structure of 1,5-hexadiene in an antiperiplanar conformation. The antiperiplanar conformation was drawn on GaussView5.0, the dihedral angle was modified to 180° and in order to obtain the correct point group, the function 'Symmetrize' was used to obtain the desired point group. The optimization was run using Hartee Fock level of theory and the 3-21 basis set.

After the calculation was run, the energy was found to be -231.69079 Hartee units. The point group was determined to be C1.

Optimisation log file here

summary data	1,5-hexadiene antiperiplanar	Point Group
File:React anti1stm13.mol	3-21G optimised 1,5 hexadiene app molecule	C1

1,5-hexadiene Gauche conformer

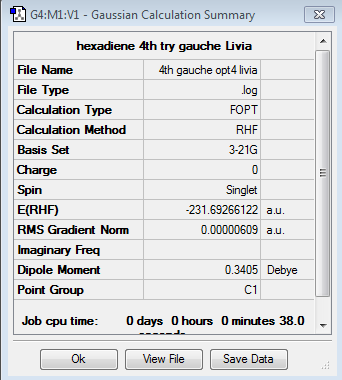
The second section of the tutorial asked to optimize the structure of 1,5-hexadiene, this time in a gauche conformation (dihedral angle 60°). After the calculation was run using Hartee Fock theory and 3-21G basis set, the energy was found to be -231.692661 Hartee units and the point group C1.

Optimisation log file here

summary data	1,5-hexadiene gauche	Point Group
	3-21G optimised 1,5 hexadiene gauche molecule	C1

From the results obtained above, it is found that the gauche conformation is the lowest energy one which is not the expected result. Usually antiperiplanar conformations are lower in energy because of the lower repulsion between the side groups and en electronic stabilisation through hyperconjugation (Does hyperconjugation only occur in the anti configuration? João (talk) 12:11, 10 February 2015 (UTC)). From the gauche conformer it can be observed that the repulsion between the hydrogen atoms is not extensive and a stabilizing interaction between the π orbital and the vinyl proton is present as well as delocalisation through the п bonds of the carbon-carbon double bond.

It is possible to compare the obtained conformers to appendix 1

By comparing the energies, it is obtained that the antiperiplanar structure corresponds to the anti4 conformer while the obtained gauche conformer is the gauche3 conformer, demonstrating the optimizations were run effectively.

Anti2 1,5 hexadiene Conformer

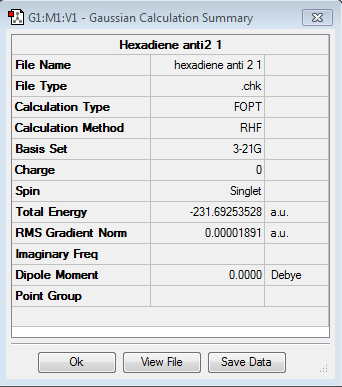
The Anti2 confomer structure was drawn on GaussView by trying to replicate the structure found in Appendix 1 and an optimization using the same procedure as described previously (HF/3-21G)

Optimisation log file [[Media:HEXADIENE_ANTI_2_1.LOG| here]

summary data	1,5-hexadiene antiperiplanar (anti2 conformer)	Point Group	Numbered molecule
	3-21G optimised 1,5 hexadiene app molecule	Ci

The energy computed is -231.692535 compared to Appendix 1 value for the Anti2 conformer which is -231.69254 we can assume the confomers are the same. In addition also the point group, Ci, corresponds to the Anti2 confomer shown in Appendix1.

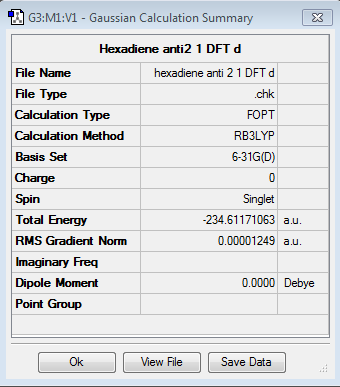
Optimization of anti2 1,5 hexadiene using Density Functional Theory

A different level of theory, DFT/B3LYP is used now, which allows a more precise optimization to be run as the electron correlation effects are taken into account.

Optimisation log file [[Media:HEXADIENE_ANTI_2_1_OPT_631G_1.LOG| here]

summary data	1,5-hexadiene antiperiplanar (anti2 conformer)	Point Group	Numbered molecule
	6-31G optimised 1,5 hexadiene app molecule	Ci

When comparing the two conformers it is shown that the energies computed are different: hexadiene anti2 energy is equal to -231.692535 hartee units while the energy calculated using density function theory is -234.61171063 hartee units. Upon comparing the two different calculation methods, a different Dihedral angle is calculated: for the Hartee Fock method, a dihedral angle of 114.66880° is observed for the last 4 carbons while using Density Function Theory, the dihedral angle is 118.76969°. The angles for the rest of the molecular are similar to an extension of one degree maximum of difference. In addition, bond lenghts are compared:

bond lenghts

	C1-C4	C4-C6	C6-C9
r(Hartee Fock) Å	1.316	1.509	1.553
r(DFT) Å	1.338	1.507	1.555

As a result, the difference in the geometry structure of the conformers are not great but the difference in energy with the DFT B3LYP/6-31G(d) optimization being lower than HF/3-21G by approximately 3 a.u. demonstrates the better efficiency when using DFT theory (Why does it demonstrate that? João (talk) 12:11, 10 February 2015 (UTC)).

Frequency at 298.15 K

Frequency calculation using the DFT level of theory and B3LYP-6-31G sup>* basis set were conducted using the B3LYP-6-31G^* optimized structure. From the result file, the following data was reported:

• Sum of electronic and zero-point Energies= -234.469219 a.u
• Sum of electronic and thermal Energies= -234.461869 a.u
• Sum of electronic and thermal Enthalpies= -234.460925 a.u
• Sum of electronic and thermal Free Energies= -234.500809 a.u

The sum of electronic and zero point energies corresponds to the energy of the molecule at 0K which includes the zero-point vibrational energy. The sum of the electronic and thermal energies corresponds to the energy of the molecule at 298.15K (Under which assumptions? João (talk) 12:11, 10 February 2015 (UTC)), this energy is different from the previous one as it contains the contribution of vibrational, rotational end translational energy. The sum of the electronic and thermal enthalpies differs from the sum of electronic and thermal energies as it contains an additional term, RT (product of gas constant and temperature), as H(enthalpy)= E(energy) +RT (Under which conditions is this the case? João (talk) 12:11, 10 February 2015 (UTC)). The energy should therefore be higher (less negative)and is in agreement with the values reported. The sum of electronic and thermal Free energies corresponds to the entropic contribution to the energy (G=H-TS), where S is the entropy, consequently the energy value is lower (more negative) (Do you have an idea on how is the entropy estimated? João (talk) 12:11, 10 February 2015 (UTC)).

In additional all the values of the frequencies reported in the vibration results are real confirming the presence of a minimum rather than a transition state (should have an imaginary frequency).

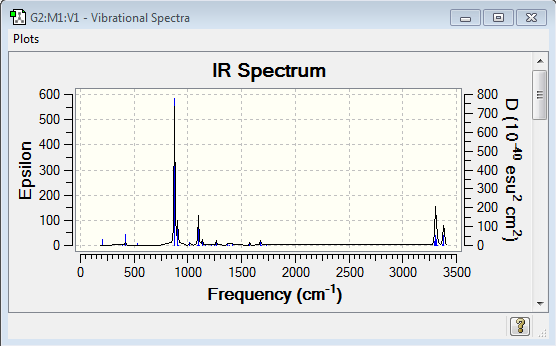
A simulation of the vibrations spectrum is shown below

IR spectrum at 298.15K

From the spectrum it is shown that there is a large range of frequencies in the 3233-3012 cm^-1 region, reflecting the sp² and sp³ stretches. By looking at the displacement vector option in the Vibrations result file and animating the vibration, it is noted that the sp² stretching frequencies are found at a higher frequency compared to the sp³ones. The asymmetric C=C stretch is found at 1734.47 cm^-1. A strong peak is shown at 940 cm^-1, this corresponds to the terminal CH₂ groups wag.

Calculation of frequency at 0.00001 K

(Do frequencies actually change with temperature? João (talk) 17:32, 10 February 2015 (UTC))

A very small temperature was used to calculate the frequencies to a value that would be close the 0K (which is experimentally impossible to achieve).

• Sum of electronic and zero-point Energies= -234.469208 a.u
• Sum of electronic and thermal Energies= -234.469208 a.u
• Sum of electronic and thermal Enthalpies= -234.469208 a.u
• Sum of electronic and thermal Free Energies= -234.469208 a.u

It is noted that the above reported values are all equal. The reason behind this behaviour is that at very small temperatures there is no rotational, vibrational (How does zero-point energy come into this picture? João (talk) 17:32, 10 February 2015 (UTC)) or translational contribution to the energy of the molecule as there is not enough energy to excite the molecule to higher energy levels. As a result, at very small temperature the RT term doesn't contribute to the energy so does not the entropy.

Optimizing the "Chair" and "Boat" Transition Structures

1. Optimizing Chair Transition structure by computing force constants at the beginning of calculation

To simulate a chair transition state, an allyl fragment (CH₂CHCH₂) was drawn on GaussView (Did you optimize the allyl fragment individually? João (talk) 17:32, 10 February 2015 (UTC)) and then it was replicated so that two the final structure resembled that of a chair transition state. A Hartee Fock optimisation+frequency to a TS (Berny) calculation was performed and the additional keyword=Noeigen was added to prevent the calculation from crashing in the case that more than one imaginary frequency was presented in the structure:

the expected imaginary frequency of 818 cm^-1 is shown in the frequency results. In addition the energy is -231.61932182 a.u.

Spectrum	Chair Transition Optimization
	3-21G optimised chair transition molecule

(You report the spectrum of the transition state structure. Would this spectrum be easily obtained? João (talk) 17:32, 10 February 2015 (UTC))

Motion

2. Optimizing Chair transition structure using the redundant coordinate editor

This time, the transition state was optimized using HF/3-21G by freezing the coordinates of the terminal carbons bonds to ~2.1Å and differentiating along the coordinates. The force constants were this time only calculated for the bond forming/breaking bond rather than for the entire molecule.

The energy calculated for the optimized structure is - 231.61932244 a.u. To prove that the optimized structure is a transition state, the frequency results were checked and an imaginary frequency at -817.97 cm^-1 was detected.

Opt=Mod redundant optimized chair transition structure

The bond lenghts of the two structures obtained from the different calculation methods were compared:

bond lenghts

Method	C1-C1 Å	C3-C3 Å
r(method 1.)	2.02204	2.02135
r(method2.)	2.02047	2.02064

Comparing the two computed transition structures they appear to be the same; from the obtained energies -231.61932182 a.u. for the first method compared to - 231.61932244 a.u. for the second one, we can say that both methods give similar results. The bond lenghts as well are very similar with the second method optimizing the transition structure slightly better.

Optimizing the boat transition structure

A different procedure was used to optimize the boat transition structure. HF/3-21G was used as for the previous optimizations but it was optimized to a QST2 transition state as it provides an efficient way to locate the transition structure without requiring any knowledge of its structure. Only a suitable structure of the product and reactant is required and in addition the numbering of the atoms in the reactant and product must be identical so that they can be consistent with the reaction's pathway.

The reactant and product structures were obtained using the anti2 conformer of 1,5-hexadiene. A first optimization calculation was run but it failed as the obtained structure was not the boat transition structure.

QST2 optimization of boat transition structure failed

Consequently, the dihedral angle along the four central carbons was changed to 0° in both the product and reactant and then the C2-C3-C4 and C3-C4-C5 angle was changed to 100° to give the following structures:

Now the optimization using QST2 gave as a result a boat transition structure which was confirmed by the presence of an imaginary frequency at -839.94 cm^-1 and en energy of -231.60280200 a.u.

reactant and product	boat transition structure

By looking at the transition structures of the boat and chair transition state conformations, it is very difficult, to predict which of the 1,5-hexadiene conformers it will lead to during the course of the reaction. Therefore another method needs to be developed.

Intrisic reaction Coordinate

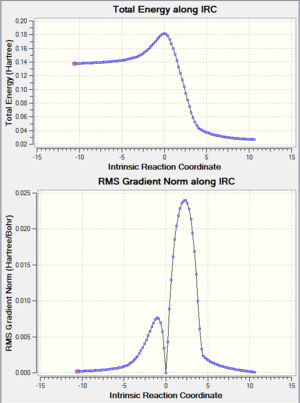
In order to determine which conformer of 1,5-hexadiene the transition state will lead to, the intrinsic reaction coordinate (IRC) method has been developed. By using this method, the minimum energy pathway is followed creating multiple points (obtained by changing the coordinates of the atoms by very small amounts) in the direction where the gradient of the energy surface is steeper. The calculation was only run in the forward direction from the transition state to the product as the product and reactants are the same and hence have the same energy.

First of all a IRC calculation was performed using the chair transition state conformation obtained using the redundant coordinate editor (Part 2.) The guess method had to be changed to default and the the frozen coordinates were removed (Not sure I follow what you are saying here. To run an IRC you simply need a transition state structure, it is not important how that structure was obteined. João (talk) 17:32, 10 February 2015 (UTC)). From the 50 points calculation, the following results are found: out fo the 50 point steps, the IRC calculation stopped at the 44^th point meaning that a minimum had been found. In order to confirm that the product lies on a plateau, a new calculation, this time using 70 points is performed. From the potential energy surface diagram it can be observed that the same potential energy surface diagram ( 50 points) has been generated. The calculation once more stopped after the 44^th point.

IRC pathway	50 points IRC	IRC pathway for 70 steps

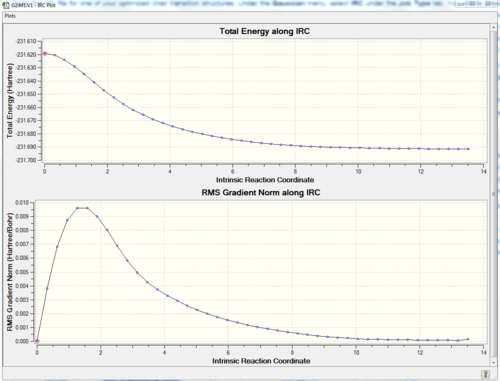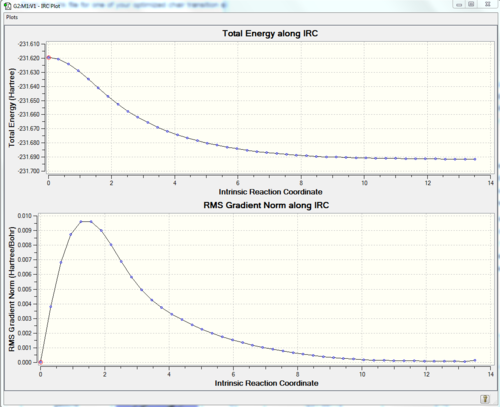A minimization was then run on the last point of the IRC calculation using Hartee Fock 3.21-G level of theory. The presence of a minimum was confirmed by the absence of an imaginary frequency and the energy was calculated to be -231.69166702 a.u. corresponding to the Gauche2 conformer found in Appendix 1. In addition the point group of the minimized conformation was C2 corresponding again to the Gauche2 conformer of 1,5-hexadiene. (How does this minimum compare with the last point of the IRC? Did the IRC stop at/close to the minimum? João (talk) 17:32, 10 February 2015 (UTC))

The log file can be found here

Minimization of point 44 along IRC

Calculation of activation energies

The chair transition state was optimized using the chair optimized structure obtained using the redundant coordinate editor. B3LYP/ 6-31G^* level of theory was used, the redundant coordinates were removed and the molecule was optimized to a transition state (Berry), calculating the force constants once. The Guess method was set to default and the Opt=noeigen keyword was added to prevent the calculation from crashing. In addition the solvation parameter was changed to "none". The results showed the presence of an imaginary frequency at -565.54 cm^-1 and the point group was determined to be C_2h

Chair	Chair transition state B3LYP vibration/ 6-31G*

For the boat transition state structure the same procedure as described above was applied. The presence of the transiton state was confirmed by the presence of an imaginary frequency at -530.20 cm^-1 and the point was determined to be C_2V.

Boat	Boat transition state B3LYP vibration/ 6-31G*

These newly optimized transition states obtained using DFT, B3LYP6-31G^* were compared to the respective chair and boat transition state optimized using HF/3-21G level of theory. The bond lenghts of the chair transition structure were compared showing a difference with the DFT/B3LYP6-31G^* method giving a structure with shorter bond lengths than HF/3-21G. Also the energies obtained from the two different level of theories can be found in the table "summary of energies" found in the next section. The energy computed using DFT, B3LYP6-31G^*, are lower in energy compared to HF/3-21G thus demonstrating once more that DFT level of theory is more accurate.

bond lenghts

Method	C1-C1 chair Å	C1-C1boat Å
r(HF/3-21G)	2.02047	2.14000
r(DFT/B3LYP6-31G*)	1.96754	2.02679

Energies calculated from frequency calculation

The energies were calculated by accessing the results file of the frequency calculations. The Electronic energy was obtained by substracting the "zero point energy" value from the "sum of electronic and zero-point energies" one. To calculate the activation energy, the energy of the anti2 reactant was substracted from the transition state energy for both 0K and 298.15K. (From this I gather that you report the activation energies without zero-point corrections. What is the reason to do this? João (talk) 17:32, 10 February 2015 (UTC))

Summary of energies (in hartree)

	HF/3-21G			B3LYP/6-31G*
	Electronic energy	Sum of electronic and zero-point energies	Sum of electronic and thermal energies	Electronic energy	Sum of electronic and zero-point energies	Sum of electronic and thermal energies
		at 0 K	at 298.15 K		at 0 K	at 298.15 K
Chair TS	-231.619323	-231.466699	-231.461340	-234.556983	-234.414878	-234.409009
Boat TS	-231.602802	-231.450928	-231.445299	-234.543093	-234.402343	-234.396008
Reactant (anti2)	-231.692535	-231.539539	-231.532565	-234.611704	-234.469208	-234.461869

Summary of activation energies (in kcal/mol)

	HF/3-21G	HF/3-21G	B3LYP/6-31G*	B3LYP/6-31G*	Expt.
	at 0 K	at 298.15 K	at 0 K	at 298.15 K	at 0 K
ΔE (Chair)	45.71	44.76	34.09	33.17	33.5 ± 0.5
ΔE (Boat)	55.60	54.76	41.96	41.33	44.7 ± 2.0

The energy was converted in kcal/mol by using the conversion of 1 a.u. (hartee-fock unit)=627.509 kcal/mol

The values obtained from the calculations above show that the B3LYP/6-31G^* level of theory shows a greater similarity to the experimental values. Especially the activation energy corresponding to the chair transition state is in good agreement with the experimental values. The absolute error value of the boat transition state is greater than the chair transition state as it is a higher energy transition state. Another reason for the small discrepancy between the obtained activation enerrgies and the experimental ones, can be attributed to the fact that the methods used in this tutorial, did not consider solvent effects and the intermolecular interaction (Was the experimental value obtained in solution? Which solvent? João (talk) 17:32, 10 February 2015 (UTC)). The boat transition state is higher in energy due to steric strain between the hydrogen atoms also sometimes referred as flag-pole interactions. Therefore the reaction pathway is more likely to go via a chair transition structure rather than the boat one. In addition from the computational methods used it is shown that both Hartree-Fock and DFT level of theory agree with the chair transition state being lower in energy as proven also by other studies

Diels-Alder Cycloaddition

The Diels-Alder reaction is defined as [4+2] cycloaddition between a diene and a dienophile in which the formation of two П C=C bond are converted into two single σ C-C bonds. The formation of the sigma bond is the driving force of the reaction as it is thermodynamically favoured due to the fact the sigma bonds are stronger than pi bonds. The reaction is defined as a cycloaddition because the transition state should proceed via a cyclic system in a concerted fashion. Diels Alder reaction can be either normal demand, where the diene contains an electron donating group so that the HOMO rises in energy while the dienophile contains an electron withdrawing group making the LUMO (lowest unoccupied molecular orbital) lower in energy and hence interacting stronger with the HOMO (highest occoupied molecular orbital). An inverse electron demand Diels-Alder reaction is one in which the diene contains an electron withdrawing group which lowers the LUMO and the dienophile has an electron donating group which raises the energy of the HOMO again making the two MOs closer in energy and hence favouring the reaction.

Cis butadiene

Cis butadiene was drawn on GaussView by joining 4 carbon trivalent units and changing the dihedral angle to 0.00°. The structure was then symmetrized to C₂V point group.

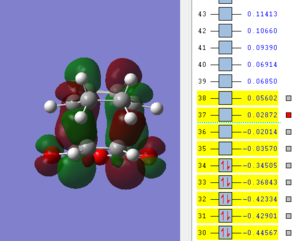
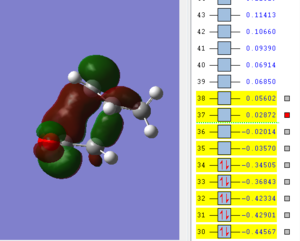
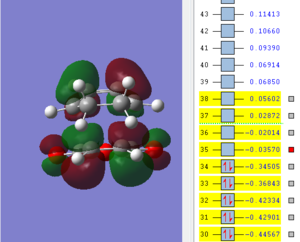
An optmization of the molecule was performed by using a new level of theory, the Semi-empirical one which differs from Hartee Fock as it is faster by applying some semplifications such as the zero-differential overlap approximation . The HOMO and LUMO were displayed by selecting the highest occupied and lowest unoccupied molecular orbital respectively. It can be established from the molecular orbitals that the HOMO is antisymmetric with respect to the yz plane (see figure 1) while the LUMO is symmetric.

HOMO of cis butadiene	LUMO of cis butadiene	Axes
		Figure1

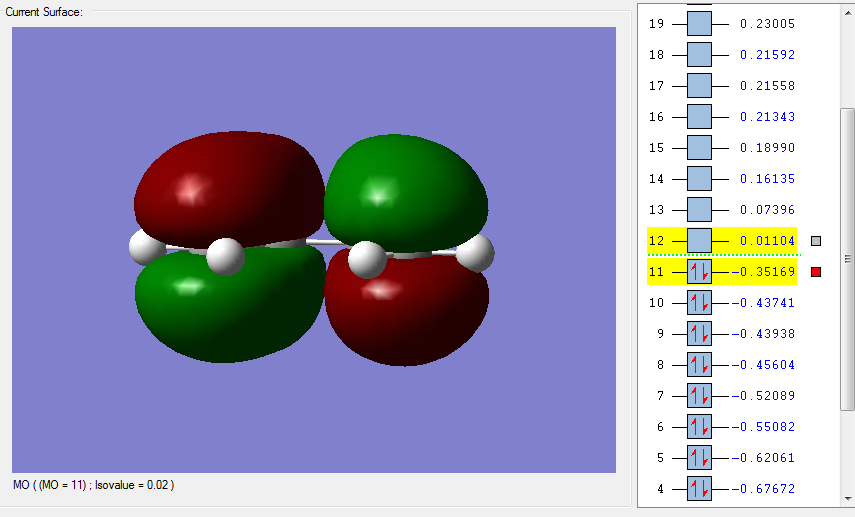
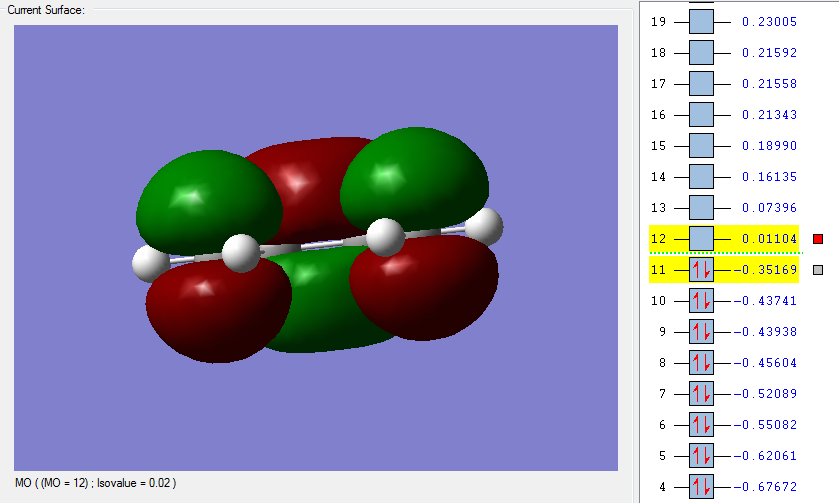
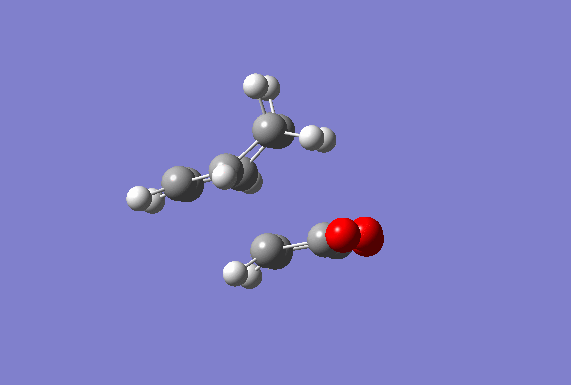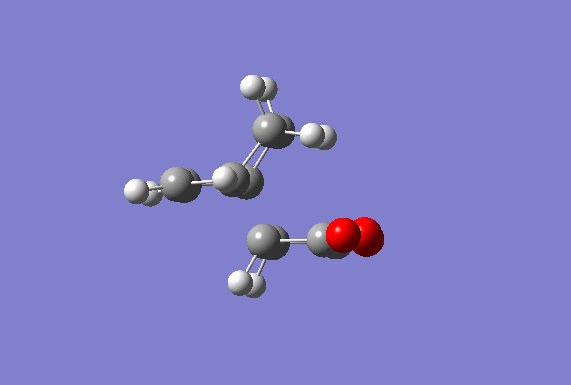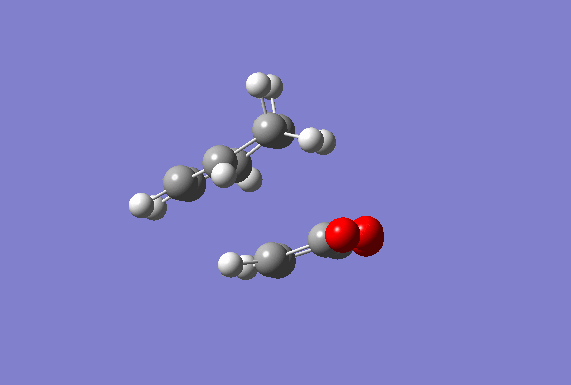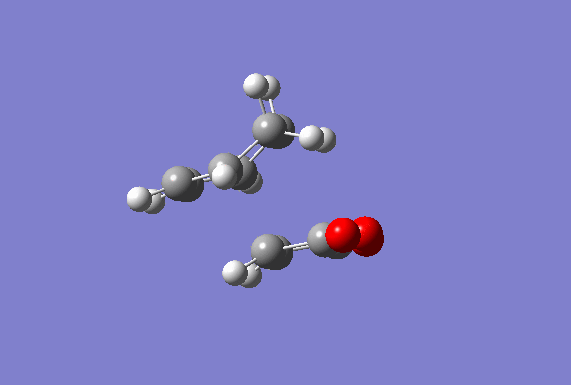
Computation of the Transition State geometry for ethene+ cis butadiene

A guess transition structure was contrucuted using the optimized cis-butadiene used from the previous part, and a molecule of ethene. The two fragments were positioned in such a way to resemble an envelope structure where the overlap between the π orbitals of cis butadiene and ethene is maximised. The structure was first symmetrized to C_s point group and then cleaned. An optimization to a transition state (Berny), was calculated using the semi empirical/ AM1 method. The optimized structure was found to have an energy of 0.1859486 a.u. The transition state was confirmed by the presence of an imaginary frequency at -955.38 cm^-1. In addition an IRC calculation on both directions using the semiemprical AM1 method was performed to visualize the reaction pathway and confirm the presence of only one transition state (If there is another transitions state, how would that show up in the IRC? João (talk) 17:32, 10 February 2015 (UTC)). From the vibration of the imaginary frequency and the IRC movie, it showed the formation of the bonds to be synchronous. The lowest positive frequency is at 212.80 cm^-1 is displayed below and corresponds to the asynchronous vibration of the molecule. From the IRC calculation it is possible to establish that the transition state is an early one as its geometry is closer in energy to the reactant rather than the product as described by the Hammond's postulate. (You seemed to have studied the wrong reaction, you seemed to be looking at ethine instead of ethene. João (talk) 17:32, 10 February 2015 (UTC))

Imaginary vibrational frequency	50 points IRC	Reaction

Positive vibrational frequency

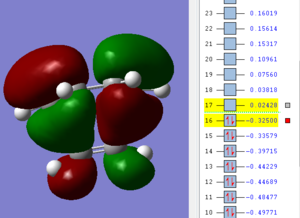
The Molecular orbitals of the transition state were visualized and compared to the reactants to identify which MOs constitute the HOMO and LUMO of the transition state. According to the Woodward-Hoffmann rules, during a pericyclic reaction, in our case a cyclo-addition, the reaction proceeds when the orbital symmetry of the reactants in preserved during all the steps of the reaction and hence also in the transition state. An approximation often used to describe cyclo-additions is the use of Frontier Molecular Orbitals (FMOs), which describes the formation of new bonds by the interaction of a HOMO of a reactant with a LUMO of another reactant. In our case, the HOMO of cis-butadiene (dienophile) is higher in energy than the HOMO of ethene (diene) as seen in the MOs diagram and thus the reaction can be defined as a normal demand Diels-Alder. From the table below it is possible to identify the constituent MOs of the transition state: the HOMO of ethene and the LUMO of butadiene combine to form the LUMO of the transition state. On the other hand, the LUMO of ethene and the HOMO of cis-butadiene combine to form the HOMO of the transition state. The reaction is allowed following the Woodward-Hoffman rules as the symmetry of the reactants is preserved in the transition state ( e.g. the HOMO of ethene is symmetric so is the LUMO of cis-butadiene and the LUMO of the transition state).

Ethene	cis-butadiene	transition state
HOMO symmetric LUMO antisymmetric	HOMO antisymmetric LUMO symmetric	HOMO antisymmetric LUMO symmetric

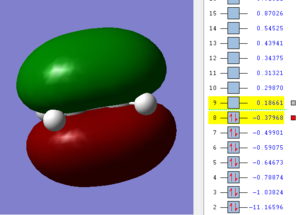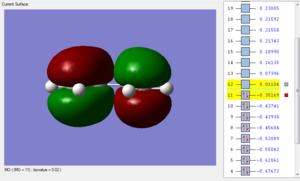In addition the envelope transition state structure was examined. The following bond lenghts were found:

bond lenghts of transition state

C5-C11 Å	C8-C13 Å	C3-C5 Å	C1-C3 Å	C1-C8 Å	transition state
2.08667	2.08889	1.38148	1.39856	1.38151

the bonds that should form during the cycloaddition reaction are C5-C11 and C8-C13; at the transition state, the distance between these two atoms is 2.08664 Å and 2.08893 Å respectively indicating that some electronic interaction is present as the Van der Waals radius of Carbon is 1.7 Å thus any distance smaller than 3.4 Å is indicative of some overlap between the two atoms. For reference, a single (sp³ ) C-C bond is usually 1.54 Å while a double bond C=C (sp²) is 1.34 Å. therefore at the transition state the bond hasn't formed yet. From the measured bond lenghts it was observed that the other C-C bonds are shorter than a single sp³ C-C bond but longer than a sp² showing that delocalization is present in the transition state.

Regioselectivity of Diels-Alder

The Diels-Alder reaction studied in this exercise is an example of a cyclo-addition between an electron rich diene (cyclohexadiene) and en electron poor dienophile (maleic anhydride). Maleic anhydride is electron poor as it contains two carbonyl groups which are electron withdrawing hence they lower the energy of the C=C double bond energy by pulling electron density away from the carbons. The reaction can proceed either via an endo or exo transition state and the energy of these geometries will be studied to determine the preferred reaction pathway. As maleic anhydride is lower in energy it is speculated that the LUMO will be lowered in energy while the HOMO of the cyclo-hexadiene will raise in energy allowing for a better interaction between these orbitals as the energy gap is lowered.

Exo transition structure

A guess transition structure was drawn on Gauss view by adding two different fragments together. The two fragments were maleic anhydride and cyclohexene; the two fragments were set apart at approximately 2.0 Å and an optimization to a transition state (Berny) using the semi-empirical AM-1 method was used. The optimization yielded the exo transition state which was confirmed by the presence of an imaginary frequency at -812.21 cm^-1 and an energy of -0.05041977 a.u.

bond lenghts of exo transition state

C3-C17 Å	C2-C16 Å	C11-C13 Å	C11-C3 Å	C1-C4 Å	C3-C4	C16-C17	C21-C17	H7-O15	transition state
2.17097	2.16992	1.39675	1.39432	1.52206	1.48976	1.41016	1.48815	2.75696

From the distance between the C3-C17 it can be seen that as for the previous exercise, the distance between the atoms is shorter than the sum of the Van der Waals radii of Carbon (3.4 Å) indicating the presence of some interaction between the two atoms. From the other distances it is also shown that delocalization is present in the transition state as all the distances are shorter than a single C-C bond but longer than a double C=C one. In addition the distance between the hydrogen on the bridge and maleic anhydride oxygen (C=O)-O-(C=O) was investigated and was found to be 2.75696 Å. Considering that the Van Der Waals radius of Oxygen and Hydrogen is 1.52 Å and 1.2 Å respectively then the distance between the two atoms in order to have some Van der Waals interactions should be 2.72 Å which is shorter than the measured distance in the exo form, meaning that no interaction is present. In addition the dihedral angle between H(19)-C(17)-C(21)-O(23) changed from the reactant being 0.0000° to -26.18907° in the transition state to account for the repulsion between C3 and H19 being 2.42 Å (sum of V.d.W radii of C+H= 2.9 Å)

The molecular orbitals of the transition state can be found in the table below:

LUMO+2	LUMO+2 side view	LUMO+1
LUMO +2 antisymmetric	LUMO +2 side views	LUMO+1 symmetric
LUMO	HOMO	HOMO-1
LUMO antisymmetric	HOMO antisymmetric	HOMO -1 symmetric

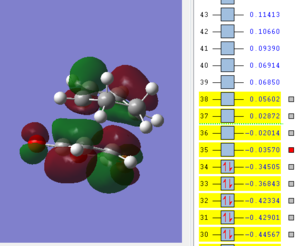The molecular orbitals of the exo transition state show no secondary orbital overlap, the HOMO and LUMO of both exo and endo transition state is antisymmetric. When comparing the LUMO+1 and higher orbitals the symmetry between the exo and endo changes with for example the LUMO+2 in the exo t.s being antsymmetric while symmetric for the endo t.s. Secondary orbital overlap is not observed in the exo transition state as the C=O π^* and C=C double bond are far apart and can't interact.

An IRC calculation was performed from the transition state using the semi-empirical AM1 method to visualize the reaction path from the transition state to the product and reactants to follow the reaction pathway. It is shown that the formation of the bond in the cyclo-addition is concerted and occurs with syn addition of the two fragments.

reaction pathway

Endo transition structure

The endo transition state was identified by orienting the two fragments of maleic anhydride and cyclohexadiene in such a way that the C=O groups of maleic anhydride were perpendicular to the cyclohexadiene fragment. An optimization was run using semi-empirical level of theory and AM1 method. The calculation gave the endo transition state structure which was confirmed by the presence of an imaginary frequency at -806.29 cm^-1 an en energy of -0.05150478 a.u.

The endo transition state is analyzed below:

bond lenghts of endo transition state

C11-C3 Å	C11-C13 Å	C4-C3 Å	C1-C4 Å	C11-C21 Å	C3-C17 Å	O23-H12 Å	H19-C4 Å	H12-O23 Å	transition state
1.39310	1.39727	1.49058	1.52299	2.89224	2.16232	3.31665	2.66559	3.31665

From the bond lenghts calculated above, it is possible to see that there is delocalization present in the transition state as the C-C bond lenghts are in between 1.34 Å and 1.54 Å which are respectively, the single C-C bond lenght and the double C=C one.In addition the distance between C11 and C21 is 2.89 Å demonstrating that some interaction is present between the two atoms as the sum of V.d.W radii is 3.4 Å while the distance measured is shorter than this value.In addition the distance between the the hydrogen on the cyclohexadiene and the oxygen on maleic anhydride was measured to be ~3.32 Å which is longer than the minimum distance required for some interaction to occur (V.d.W radii of Oxygen+Hydrogen=2.72 Å). The dihedral angle for H19-C17-C16-H18 as also observed for the exo transition state changed from 0.0000° in the reactant to -0.01852° in the transition state to account for steric repulsion between the C4 and H19. In fact the distance between these two atoms is 2.66559 Åwhich is shorter than the sum of the V.d.W radii of the two atoms (2.9 Å). When comparing these distance with the exo form, it is observed than in the exo transition state, the distance is 2.42 Å which is shorter and hence more steric repulsion is observed for the exo form therefore it is more strained than the endo trasition state.

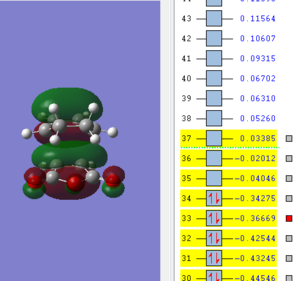
The molecular orbitals for the endo transition state are shown below:

LUMO+3	LUMO+3 side view	LUMO+2
LUMO +3 antisymmetric	LUMO +3 side view	LUMO+2 symmetric
LUMO+2 sideviews	LUMO+1	LUMO+1 side view
LUMO+2 side view	LUMO +1 antisymmetric	LUMO+1 side view
LUMO	HOMO	HOMO-1
LUMO antisymmetric	HOMO antisymmetric	HOMO-1 symmetric

From the plotted molecular orbitals it is possible to observe that secondary order overlap is present in the LUMO+2 MO but not in the HOMO. The HOMO of the endo transition state is antisymmetric with respect to the yz plane in Figure1. The fact that secondary orbital overlap is present in the LUMO+2 and LUMO+3 rather than the HOMO could be caused by the fact that in the transition state, the electrons molecular orbitals are delocalized (I don't quite see why orbital delocalization is a cause for this. João (talk) 17:32, 10 February 2015 (UTC)). The favourable overlap is seen between the π C=C double bond of the diene and the π^* of the C=O bond. The fact that the oxygen is an electron withdrawing group and hence lower in energy dictates the coefficient of the orbitals, as a result the O p-orbital is bigger in the π orbital while in the π^* (higher in energy) the C p-orbital is greater, thus interacts better with the diene. In addition from the image below it is possible to see that both the primary and secondary orbital overlap proceed suprafacially therefore this reaction can be defined as a [4+2] (4 electrons contributing from the diene and 2 from the dienophile)thermally allowed suprafacial cyclo-addition. In addition, the imaginary frequency vibrations desplayed below show the formation of the bond to happen in a concerted fashion leading to the respective product.

orbital overlap shown for exo on the left and endo on the right

Exo Imaginary frequency	Endo Imaginary frequency

Activation energies

In order to establish the preferred product of the reaction between maleic anhydride and cyclohexadiene, the activation energies were calculated. The reactants, were drawn on GaussView 5.0, symmetrized and then optimized to a minimum using the semi-empirical/AM1 level of theory to be consistent with the previous calculations. The energies of the reactants and the transition states can be found below.

activation energies

	maleic anhydride	1,3 cyclohexadiene	exo transition state	endo transition state	ΔE exo	ΔE endo
Energy a.u.	-0.12182358	0.03495306	-0.05041977	-0.05150478	0.03645075	0.03536574

The energy was converted in kcal/mol by using the conversion of 1 a.u. (hartee-fock unit)=627.509 kcal/mol to give an activation energy for the exo and endo of 22.87314 kcal/mol and 22.19232 kcal/mol respectively. This means that the difference between the exo and the endo activation energy is of 0.68 kcal/mol. As a result the formation of the endo product is favoured as it requires less energy, this observation is in agreement with other computational studies

Conclusion

In conclusion, the Diels-Alder reaction was studied for two different cycloaddition. For both reactions, the transition states were successfully identified using the AM1-Semi empirical method and all showed to have an imaginary frequency. In addition, the selectivity of the endo product over the exo one was discussed in terms of activation energies and secondary orbital overlap. Other computational methods could have been used as well to yield more accurate results as DFT or HF level of theory but as the semi-empirical one was faster and gave good results it was used instead. It must be noted that in general computational studies omit the interaction between molecules and solvent and thus study the molecule as if it behaved as an ideal gas. In addition it must be noted that in all these exercises, the transition structure was guessed but some knowledge of its structure was known as they are well known reaction. In the case of an unknown reaction, other solutions and methods as the QST2 need to be find since the transition structure cannot be completely guessed.

References

<references>