Rep:Mod:lkjh1234
Imperial College
London
MODULE 3 - Experiment 3: The Transition State
Note: This page is optimized for a window of width ~1400px
|
|
The Cope Rearrangement Tutorial
This section involves locating the low-energy minima and transition structure on the C6H10 potential energy surface for the [3,3]-sigmatropic shift Cope rearrangement of 1,5-hexadiene:

Optimizing the Reactants and Products
The procedure was followed as per instruction with 500MB of memory being utilised and the anti structure was optimized at the HF/3-21G level of theory. If not stated and unless stated otherwise, the procedure was followed as per instruction.
|  |
|||||||||||||
This is structure anti2 from the table, and has Ci symmetry.
Next the equivalent gauche structure was constructed. I would expect this to have a higher energy due to a greater steric interaction of the terminal methylene hydrogens and anti-substituted ethane structures are typically lower in energy than gauche structures.
|
 |
||||||||||||
This is structure gauche1 from the table.
This was indeed observed to be the case, with a higher energy being obtained for the gauche structure. From the above I would expect the lowest energy conformation to be one in which the central 4 carbons were of anti geometry, and possibly had the two alkenes pointing away from each other (as in the above calculation). Thus I will try another geometry in which the two alkenes are a bit more random and have gauche orientation to each other (maintaining the central anti symmetry) to see if this is of lower or higher energy.
|
||||||||||||
This is structure anti4 from the table (energy -231.69097 a.u.).
As expected this is not as stable a conformation as anti2 although it is pretty close in energy and is notably more stable than the gauche conformation.
Structure anti2 has already been identified and has an energy that matches perfectly with that in the table (my energy=-231.692535 a.u. (6 d.p.), table energy=-231.69254 a.u.). Since this structure is clearly the one given in the table, it will be optimized at the B3LYP/6-31G*. A summary of the results obtained is given below:
| |||||||||||||
Despite being a few atomic units lower in energy, the optimized structure at a higher level of theory doesn't appear to have any different geometry than that at a lower level.
From the optimized B3LYP/6-31G* structure, a frequency analysis was run. No imaginary (negative value) frequencies were observed. This analysis was performed to to allow comparison of the calculated energies with experimentally measured values.
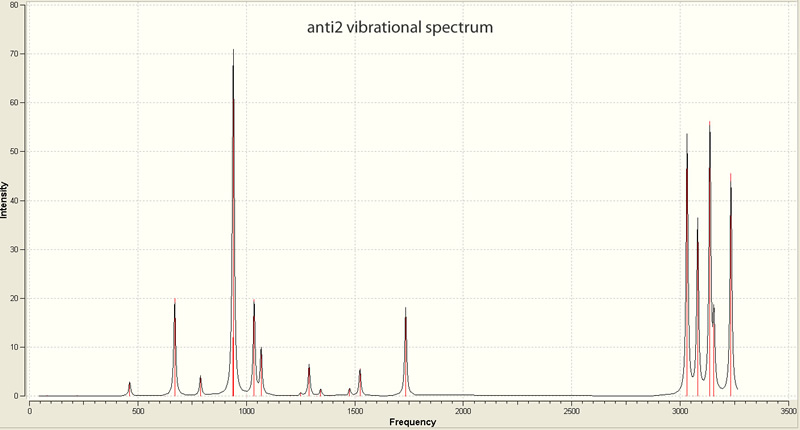
| |||||||||||
These were then re-calculated at 0K and 1 atm of pressure to yield the following results:
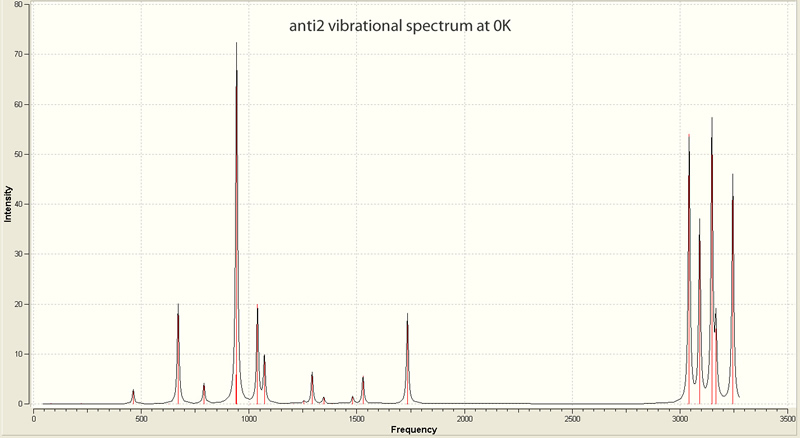
| |||||||||||
Optimizing the "Chair" and "Boat" Transition Structures
b) The structure was built by positioning two optimised (HF/3-21G) C3H5 allyl fragments approximately 2.2Å apart in a (roughly) chair-like T.S.. This structure was optimised at the HF/3-21G level of theory. (Note: the distance between the ends of the allyl fragments was set to 2.20184Å.)
The optimised structure given in appendix 2 was obtained, with an imaginary frequency obtained of -817.945 cm-1. This did indeed correspond to the Cope Rearrangement.
|
 |
d) The second optimization was performed giving a structure very visually similar to that previously obtained in b). However the bond-breaking/forming lengths are now 2.02099 and 2.02084, whereas those for the first optimization were 2.01996 and 2.02040. Despite this, the two structures appear virtually identical.
e) The boat transition structure was optimized using the QST2 method. The chk file corresponding to the 6-31G level optimisation of the anti2 reactant was then opened. The two structures were then positioned side-by-side and renumbered accordingly.
The job did fail but when I tried to view the .chk fail it killed Gaussian.
When the job was re-run with the fixed geometry it failed again. I realised this was because although the C atom labels had been changed, the H atoms of the two structures no longer correlated. Thus this was corrected and the job re-run. It failed again so I specified the opt-noeigen parameter (since the job ran for quite a while before failing). Again, it was re-run and eventually Ia successful job was obtained by ensuring that all of the hydrogen atom labels corresponded precisely.
|
 |
There was only one imaginary frequency at -840.007 cm-1, and this indeed corresponds to the Cope Rearrangement.
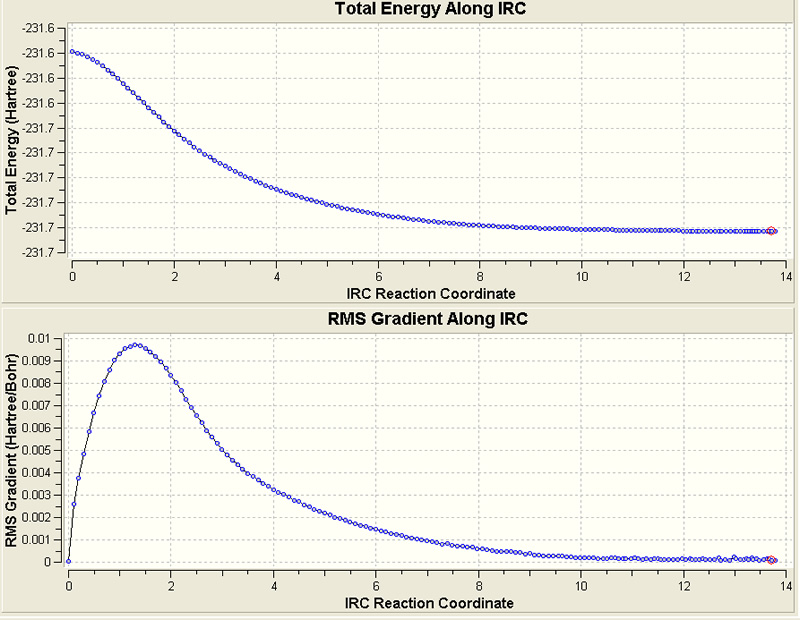
f) The boat TS doesn't really look like any of the conformers of 1,5-hexadiene, the chair T.S. (with a lenient approach) looks like anti2). The minimum energy path was then followed by employing the Intrinsic Reaction Coordinate method. The chk file for the optimized chair transition structure was opened, the reaction coordinate was only calculated in the forward direction and the force constants were only calculated once, at the beginning of the calculation. As suggested, the calculation was performed with 50 points.
As predicted this did not reach a potential minimum.
i) First, a normal optimization was run from the last point of the IRC (this was done by copying and pasting this point into a new window. A T.S.(berny) optimization was then run in which the force constants were calculated once, and the optimisation parameter 'opt=noeigen' was specified). This gave the gauche4 conformation, with energy -231.68504554 a.u..
ii) The IRC method was then repeated with 400 points (this was performed on the SCAN service)
This took over 3 hours on the SCAN System but produced very good results, converging to a (lower) energy of -231.69156959.
g) The transition stated needed to be optimised at the b3lyp/6-31g* level.
to do this, the job type opt+freq was selected. It was then optimized to a TS(Berny), the force constants were calculated once, opt=noeigen was specified and a DFT calculation at the B3LYP level with a 6-31g* basis set was performed (Note: I had to remove solvent=water and guess=read). Both were then submitted to SCAN in the interest of saving time.
The Diels Alder Cycloaddition
This section involves the characterization of the transition structure using the AM1 semi-empirical molecular orbital method (specifically the QST2 method). This is followed by an observation of the shape of some of the molecular orbitals of this system. Since the factors that control the nature of the transition state are of quantum mechanical origin, analytical methods of a quantum mechanical basis are required.
Exercise
Calculations were started with the AM1 semi-empirical molecular orbital method.
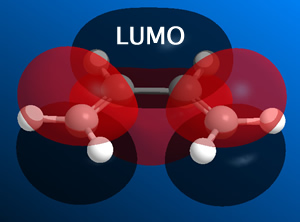
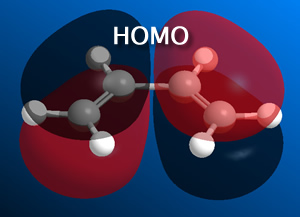
i) Cis-butadiene was constructed in Gaussian and this was optimized at a basic level ('pop=full' was included for the MO analysis).
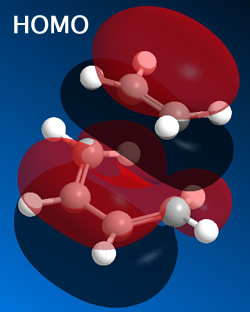
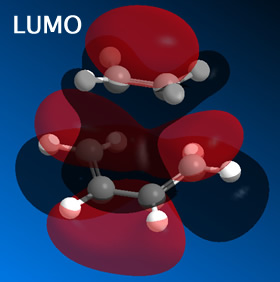
From this it was determined that the HOMO is anti-symmetric with respect to a plane, whilst the LUMO is symmetric with respect to a plane.
 |
 |
ii) Computation of Transition State geometry for the prototype reaction and an examination of the nature of the reaction path.
The bicyclo system given was created bibcyclic in Chembio 3D. This was then opened in Gaussview. The requisite bonds were deleted to produce the rough transition state structure. The first effort was made using the TS(berny) method. This was a failure since one of the hydrogens tried to bond, instead of one of the carbons..cheeky devil!!
Thus I tried again, taking more care to get the hydrogens into positions more similar to those they should adopt in the final product. From this I obtained a twisting vibration. This doesn't really seem like the T.S. so a transition state structure was calculated using the QST2 method:
Bam! Using the QST2 method (calc. force constants once, opt=noeigen, hf/3-21g), starting with the fragments below, I got the correct transition state. One imaginary frequency= -818.382 cm-1 (int=9.2969) and energy= -231.60320847 a.u.
This transition state was then optimised at the 6-31G* level (ts(berny), opt=noeigen, had to remove solvent=water, turned on MOs with pop=full and submitted to scan). This gave a structure with an energy of -234.54389656 a.u. and a vibrational frequency of -524.876cm-1.
 |
 |
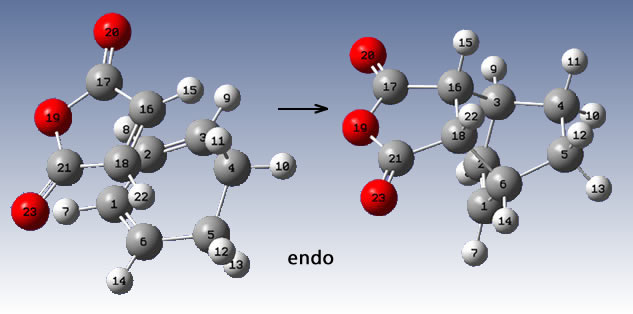
iii) The regioselectivity of the Diels Alder Reaction
Maleic anhydride and cyclohexa-1,3-diene were first made and optimised using ChemBio3D and molecular dynamics.
The products were also made and optimised using ChemBio3D molecular mechanics.
The QST2 method (as before) was employed with the following arrangments prior to the optimisation:
 |
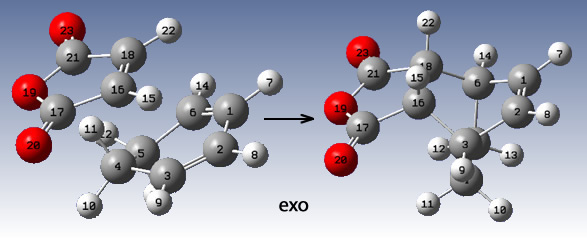 |
This yielded the correct two transition states:
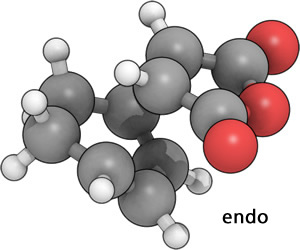 |
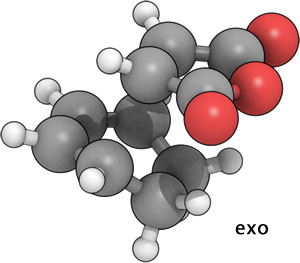 |
As expected, even at this low level of calculation, the exo T.S. is higher in energy. (exo= -605.60359123 a.u., endo= -605.61036822 a.u.).
The transition states were then re-optimised at the 6-31G* level with MO analysis switched on (Note:These were submitted to SCAN) (solvent=water had to be removed again, opt=noeigen, pop=full)
Again as expected the exo conformation was higher in energy :) (exo = -612.67931094 a.u., endo = -612.68339670 a.u.).
The HOMO (and LUMO) were then plotted for both the endo and exo forms.
 |
 |
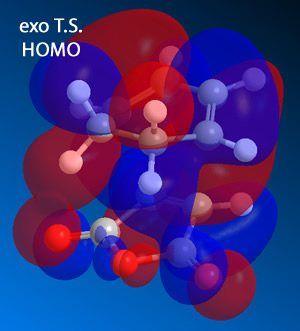 |
 |
The exo partly formed σ c-c bond lengths were isolated as 2.29054Å and 2.29060Å. Whilst the sigma bonds present in the hexadiene dienes were 1.40343Å. The diene bonds themselves were 1.39142Å and 1.39143Å. The next two bonds progressing towards the 'sigma end' were isolated as 1.51453Å and 1.51453Å. The sigma bond at the end is 1.55838Å. The maleic anhydride C=C is 1.39793Å, whilst the other two C-C bonds present in this system have lengths 1.47942Å and 1.47942Å.
The endo partly formed σ C-C bond lengths= 2.26835Å and 2.26834. The sigma bond between hexadiene dienes = 1.40306Å, whilst the diene bonds themselves have lenghts 1.39126Å and 1.39126Å. The next two towards sigma end have lengths 1.51508Å and 1.51508L. The bond at the sigma end has length 1.55822.The maleic anhydride C=C 1.39401Å and the other two C-C bond lengths are 1.47950Å and 1.47950Å respectively.
The exo through space distance between the carbon of maleic anhydride and the corresponding CH2-CH2 group carbon = 3.02764Å and 3.02765Å. The equivalent distances for the endo conformation= 2.98978Å and 2.98977.
The ethylene cis-butadiene partly formed σ C-C bond lengths= 2.27238Å and 2.27239Ǎ respectively.
The vibration corresponding to the reaction path at the transition state is a synchronous formation of bonds, whilst the lowest positive frequency (a kind of clockwise-anticlockwise twisting motion viewed from above) is evidently an asynchronous bond formation.
