Rep:Mod:littleliana3
Huijun Liu's Computational lab module 3
Week 1: The Cope Rearrangement
Optimization of Reactants and Products
The objectives of this part was to locate the low-energy minima and transition structures on the C6H10 potential energy surface and to determine the preferred reaction mechanism for the cope rearrangement reaction. This is done via gaussview and used of the program was practiced.
1,5 hexadiene HF/3-21G Optimization
The full log file for the anti conformation can be found here
| File type | .chk |
| Calculation type | FOPT |
| Calculation method | RHF |
| Basis set | 3-21G |
| Charge | 0 |
| Spin | Singlet |
| Total Energy (a.u.) | -231.69097055 |
| Gradient (a.u.) | 0.00001256 |
| Dipole moment (D) | 0.2957 |
| Point Group | C1 |
| Job cpu time | 21.0 sec |
An hexadiene gauche conformation molecule was created and optimized. it can be expected that it's energy would be higher then that of the "anti" molecule since it would have to steric strain.
The full log file can be found here
| File type | .chk |
| Calculation type | FOPT |
| Calculation method | RHF |
| Basis set | 3-21G |
| Charge | 0 |
| Spin | Singlet |
| Total Energy (a.u.) | -231.69166702 |
| Gradient (a.u.) | 0.00000744 |
| Dipole moment (D) | 0.3805 |
| Point Group | C2/C1 |
| Job cpu time | 21.0 sec |
From the results above, it can be seen that the gauche - conformation has a lower energy then the anti, so the gauche conformation is expected to have the lowest energy somehow, thus the gauche conformation is investigated to try to lower it's energy even more.
The next try gave a gauche molecule of energy: -231.69153035 a.u and an point group of C2, which has an energy higher then the run above, so anther gauche conformer was tried.
A third run was tied but the same results from the second optimization was obtained. A fourth gauche run yield a structure with an energy of -231.69266120 a.u and an point group of C1
The full log file of the last run can be found here
Comparison to appendix in instructions, here is a list of my calculations to the appendix structures:
- 1st run = anti 4
- 2nd run = gauche 2
- 3rd run = gauche 4
- 4th run = gauche 2
- 5th run = gauche 3
The last run had the lowest energy in both the appendix and all of my runs.
Persise calculations of anti 2 conformer of 1,5 hexadiene
The anti 2 C1 structure was drawn in gaussview and an 3-21G optimization run on it. the 3-21G optimization had the following results
The full log file can be found here
| File type | .chk |
| Calculation type | FOPT |
| Calculation method | RHF |
| Basis set | 3-21G |
| Charge | 0 |
| Spin | Singlet |
| Total Energy (a.u.) | -231.69253526 |
| Gradient (a.u.) | 0.00002141 |
| Dipole moment (D) | 0.0000 |
| Point Group | C1 |
| Job cpu time | 21.0 sec |
The 3-21G optimized file was then optimized further by using 6-31G(d) basis set to get the following
The full log file can be found here
| File type | .chk |
| Calculation type | FOPT |
| Calculation method | RB3LYP |
| Basis set | 6-31G(D) |
| Charge | 0 |
| Spin | Singlet |
| Total Energy (a.u.) | -234.61171035 |
| Gradient (a.u.) | 0.00001356 |
| Dipole moment (D) | 0.0000 |
| Point Group | C1 |
| Job cpu time | 21.0 sec |
While going from the HF method to the DFT method, there was a significant decrease in total energy. This is due to the fact that the HF method treats 1,5-hexdiene very much like a n-butadiene molecule during it calculations, which give results with very low accuracy. When going to the DFT method, many effects that are observed in 1,5-hexdiene are account for, including the stabilization of the overall TS by orbital overlap of the antiperiplanar allyl groups of the all of the anti conformers. Thus, in DFT method, the anti conformers would have a lower energy than the gauche ones.
The geometries of the anti 2 conformers generated by DFT were as follows:
- C-C bond length = 1.54 Å
- C=C bond length = 1.35 Å
- C-C sp3-sp3 = 1.51 Å
The geometry difference between the DFT level of theory and the HF method were present, but small. However, it is noted that the values produce by the DFT method is closer to literature values known for normal C-C bonds, thus conforming that the DFT is a more accurate method than the HF method, though not so important if we only consider the molecule geometry.
An frequency analysis was run, and it was check that there were no negative or imaginary frequencies in the results section.
The full checkpoint file can be found here
The low frequencies are as follow:
Low frequencies --- -9.4848 -0.0009 -0.0007 0.0003 3.7552 13.0208
Low frequencies --- 74.2863 81.0001 121.4175
Harmonic frequencies (cm**-1), IR intensities (KM/Mole), Raman scattering
activities (A**4/AMU), depolarization ratios for plane and unpolarized
incident light, reduced masses (AMU), force constants (mDyne/A),
and normal coordinates:
1 2 3
A A A
Frequencies -- 74.2863 81.0001 121.4109
Red. masses -- 2.7380 2.6591 2.4735
Frc consts -- 0.0089 0.0103 0.0215
IR Inten -- 0.0199 0.1169 0.0000
The vibrations were check in the results section, and it was seen that there were 42 modes for this molecule, all of which are real and had positive frequencies.
An IR spectrum was generated:
 |
The result file was open and the following information retrieved:
-------------------
- Thermochemistry -
-------------------
Temperature 298.150 Kelvin. Pressure 1.00000 Atm.
Atom 1 has atomic number 6 and mass 12.00000
Atom 2 has atomic number 1 and mass 1.00783
Atom 3 has atomic number 1 and mass 1.00783
Atom 4 has atomic number 6 and mass 12.00000
Atom 5 has atomic number 1 and mass 1.00783
Atom 6 has atomic number 6 and mass 12.00000
Atom 7 has atomic number 1 and mass 1.00783
Atom 8 has atomic number 1 and mass 1.00783
Atom 9 has atomic number 6 and mass 12.00000
Atom 10 has atomic number 1 and mass 1.00783
Atom 11 has atomic number 1 and mass 1.00783
Atom 12 has atomic number 6 and mass 12.00000
Atom 13 has atomic number 1 and mass 1.00783
Atom 14 has atomic number 6 and mass 12.00000
Atom 15 has atomic number 1 and mass 1.00783
Atom 16 has atomic number 1 and mass 1.00783
Molecular mass: 82.07825 amu.
Principal axes and moments of inertia in atomic units:
1 2 3
Eigenvalues -- 110.874721352.100741373.11146
X 0.99998 -0.00351 -0.00546
Y 0.00345 0.99993 -0.01144
Z 0.00550 0.01142 0.99992
This molecule is an asymmetric top.
Rotational symmetry number 1.
Rotational temperatures (Kelvin) 0.78119 0.06406 0.06308
Rotational constants (GHZ): 16.27730 1.33477 1.31434
Zero-point vibrational energy 374151.6 (Joules/Mol)
89.42438 (Kcal/Mol)
Warning -- explicit consideration of 7 degrees of freedom as
vibrations may cause significant error
Vibrational temperatures: 106.88 116.54 174.68 317.49 501.91
(Kelvin) 567.58 665.11 900.24 963.29 1134.32
1349.79 1350.20 1352.39 1354.46 1441.94
1487.50 1490.34 1500.05 1536.83 1731.19
1799.41 1854.87 1903.99 1926.05 1931.72
1992.06 2120.42 2123.90 2171.47 2192.24
2490.62 2495.28 4347.79 4361.61 4403.03
4431.75 4511.76 4513.33 4540.01 4540.38
4652.82 4652.86
Zero-point correction= 0.142507 (Hartree/Particle)
Thermal correction to Energy= 0.149853
Thermal correction to Enthalpy= 0.150797
Thermal correction to Gibbs Free Energy= 0.110933
Sum of electronic and zero-point Energies= -234.469204
Sum of electronic and thermal Energies= -234.461857
Sum of electronic and thermal Enthalpies= -234.460913
Sum of electronic and thermal Free Energies= -234.500777
A particular note was made of the following:
- Sum of electronic and zero-point Energies= -234.469204
- Sum of electronic and thermal Energies= -234.461857
- Sum of electronic and thermal Enthalpies= -234.460913
- Sum of electronic and thermal Free Energies= -234.500777
- The Sum of electronic and zero-point Energies is the potential energy at 0 K including the zero-point vibrational energy (E = Eelec + ZPE)
- The Sum of electronic and thermal Energies is the energy at 298.15 K and 1 atm of pressure, including contributions from the translational, rotational, and vibrational energy modes at this temperature (E = E + Evib + Erot + Etrans)
- The Sum of electronic and thermal Enthalpies contains an additional correction for RT (H = E + RT) which is particularly important when looking at dissociation reactions
- The Sum of electronic and thermal Free Energies includes the entropic contribution to the free energy (G = H - TS).
Optimizing the "Chair" and "Boat" Transition Structures
Chair Transition State Structure using HF/3-21G
force constant matrix approach
A guess "chair" structure of the transition state was created and optimized to the 3-21G basis set. the following results were obtained:
The full log file can be found here
| File type | .chk |
| Calculation type | FREQ |
| Calculation method | RHF |
| Basis set | 3-21G |
| Charge | 0 |
| Spin | Singlet |
| Total Energy (a.u.) | -231.61932245 |
| Gradient (a.u.) | 0.00001297 |
| Imaginary Freq At | -817.91 |
| Point Group | C1 |
| Animation of imaginary Freq. | 
|
frozen coordinate approach
The guess transition state was optimized again using the frozen coordinate method instead.
The first time was carry out using a normal optimize to a minimum with the bond lengths fixed at 2.2 A
A second optimization was done using a transition state optimization without calculating the force constants, the result chk file showed a molecule with the bonding/breaking bond to be 2.01995 A using the inquire button, this was noted to be as expected, since we have unfrozen the structure for optimization and this shows that the actual TS "bond" interaction is actually shorter than 2.2 A.
The fully optimized log file can be found here
| File type | .chk |
| Calculation type | FREQ |
| Calculation method | RHF |
| Basis set | 3-21G |
| Charge | 0 |
| Spin | Singlet |
| Total Energy (a.u.) | -231.61932245 |
| Gradient (a.u.) | 0.00001297 |
| Imaginary Freq At | -818.02 |
| Point Group | C1 |
| Animation of imaginary Freq. | 
|
This optimization was successful since only one imaginary frequency was obtained and the animation fo this vibration clearly shows that the 2 terminal Carbon atoms moving towards each other to form a bond.
IRC Method
Assessment of optimized chair structure was carry out to try to determine which conformers of 1,5-hexadiene the optimized transition state connects to, however, from the major difference in their energies, it was soon realized that the conformer of which the reaction paths from the transitions structures will lead to can not be predicted by the above two methods alone. The IRC method, which follows the minimum energy path from a transition structure down to the two local minimums on both sides of a potential energy surface, is used to predict the correct conformer.
Initial IRC calculation
The frozen coordinated method optimized transition state check point file was used. The reaction coordinate was only computed in the forward direction only since our reaction coordinate is symmetrical. The force constant is calculated always, and IRC MAX is not used. The first calculation was done with 50 points along the IRC and the following results were obtained.
The fully optimized log file can be found here
 |
 |
 |
 |
It is clear that it hasn't reached minimum geometry since the RMS gradient was not low enough (bellow 0.0003) It is understood that a minimum geometry has been reached if the RMS gradient converges to zero.
Improved IRC calculation
An improvement on our first calculation was done by taking the outcome of the last IRC interaction and performing a normal minimization (optimization) on it. This is a very simple and quick method, but has a risk of ending up in the wrong minimum if our last IRC interaction was far from the minimum.
The fully optimized log file can be found here
 |
 |
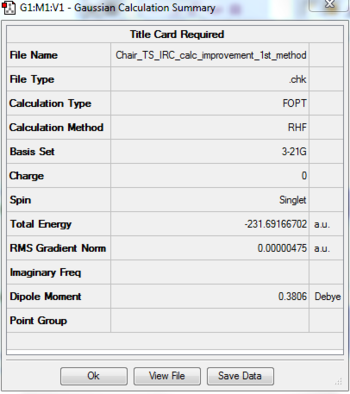The final IRC result resembles very closely to that of the Gauche 2 conformer in the appendix table of the script. Thus it can be concluded that the gauche 2 TS has the lowest energy when computing in the HF method. This does not clash with previous experimental studies and calculations that have shown the anti 2 conformer is the lowest energy TS, since this is only relevant to the DFT basis set and can not be compare to our results of which we have carry out using the HF method.
Chair Transition State Structure DFT B3LYP/6-31G (d)
A higher level basis set optimization and a frequency calculation is required to calculate the activation energy of the reaction. Comparison of the boat and chair activation energies can be found in the end. The summary after both the optimization and the frequency analysis can be found bellow:
The fully optimized log file can be found here
| File type | .chk |
| Calculation type | FREQ |
| Calculation method | RB3LYP |
| Basis set | 6-31G(D) |
| Charge | 0 |
| Spin | Singlet |
| Total Energy (a.u.) | -234.55698303 |
| Gradient (a.u.) | 0.00001252 |
| Imaginary Freq At | -565.53 |
| Animation of imaginary Freq. | 
|
It was check that the optimization was completed by checking that the forces have converged in the "items" table:
Item Value Threshold Converged? Maximum Force 0.000062 0.000450 YES RMS Force 0.000021 0.000300 YES Maximum Displacement 0.001786 0.001800 YES RMS Displacement 0.000632 0.001200 YES Predicted change in Energy=-5.044080D-07 Optimization completed. -- Stationary point found.
Summary of the geometry and energy difference between the two levels of optimization:
| Geometry Parameter | HF/3-21G | DFT B3LYP/6-31G(d) |
| C-C Interfragment Bond Length [Å] | 2.021 | 1.967 |
| C-C Bond Length [Å] | 1.389 | 1.407 |
| C-C-C Angle [°] | 120.521 | 119.951 |
| C-C-C-C Dihedral Angle [°] | 68.501 | 65.182 |
It can be seen that the geometries of the two optimization at different levels are very similar, with only a slight deviation in the dihedral angle which strongly effects the energy of the system. The energies on the other hand, is a very different story.
Summary of the Energy difference of the two optimizations:
| Type | HF/3-21G | DFT B3LYP/6-31G(d) |
| electronic energy | -231.61932245 | -234.55698303 |
| Imaginary Frequency | -818.02 | -565.53 |
As seen above, the 6-31G(d) basis set optimizes the TS to a considerably lower energy. From these results, Thus, it can be reason why it is effective to first do a optimization at a lower basis set to get our guess structure into the right region in terms of it's geometry, and than optimize it at a higher level to get a more accurate energy, since a lower basis set optimization save the later step from having to correct the geometry and the energy at the same time. Calculations of activation energies can be found at the end of the boat optimization.
Boat Transition State HF/3-21G
QST2 method
Using 3-21G basus set still, this time it's optimized to a transition state (QST2) instead of berry, the job was submitted and failed as expected.
The labels of all the atoms were changed to make sure that each correlates to the same ones between the reactant and the product, it was noted that the labels for the hydrogen are important as well!! the job failed a couple of times before it worked due to incorrect labeling.
The reactant and product geometries was modified so that they are closer to that of the boat transition structure, the dihedral angle of the central 3 Carbon atoms were changed to 0 and the angle of carbon 2-4 and 3-5 was changed to 100
The QST2 calculation was ran a second time under a new name, and a successful calculation was obtained, it was checked that only one imaginary frequency was obtained at -840.23 and the vibration was as expected, with the four terminal carbons moving towards and away from each other.
The fully optimized log file can be found here
| File type | .chk |
| Calculation type | FREQ |
| Calculation method | RHF |
| Basis set | 3-21G |
| Charge | 0 |
| Spin | Singlet |
| Total Energy (a.u.) | -231.60280222 |
| Gradient (a.u.) | 0.00004230 |
| Imaginary Freq At | -840.23 |
| Point Group | C1 |
| Animation of imaginary Freq. | 
|
Boat Transition State DFT B3LYP/6-31G (d)
The fully optimized log file can be found here
| File type | .chk |
| Calculation type | FREQ |
| Calculation method | RB3LYP |
| Basis set | 6-31G(D) |
| Charge | 0 |
| Spin | Singlet |
| Total Energy (a.u.) | -234.54309304 |
| Gradient (a.u.) | 0.00000865 |
| Imaginary Freq At | -530.57 |
| Animation of imaginary Freq. | 
|
Only one imaginary frequency observed, proves that the transition state has been reached. The log file was check to make sure that the forces have converged and that the optimizaiton was completed.
Summary of the geometry and energy difference between the two levels of optimization:
| Geometry Parameter | HF/3-21G | DFT B3LYP/6-31G(d) |
| C-C Interfragment Bond Length [Å] | 2.140 | 2.206 |
| C-C Bond Length [Å] | 1.382 | 1.393 |
| C-C-C Angle [°] | 121.669 | 122.268 |
| C-C-C-C Dihedral Angle [°] | 64.764 | 64.179 |
Summary of the Energy difference of the two optimizations:
| Type | HF/3-21G | DFT B3LYP/6-31G(d) |
| electronic energy | -231.60280222 | -234.54309304 |
| Imaginary Frequency | -840.23 | -530.57 |
Again, it is observed that the geometries of the two levels remains fairly constant while there is a large difference in the energy, as explained above. It was check that our computed values were consistant with the ones provided in the script, and that no large mistake in our calculations have occur.
Calculations of the Activation energy of the two transition states
The thermochemical section of the two transition state were taken from the log files of the frequency analysis at the DFT level, and are as follows:
 |
 |
An zero point energy was also obtained from the log file for both transition states, and use to correct the total energy by adding the zero point energy to it when using our calculated results in terms of thermodynamic quatnitites. This will eliminate systematic errors and allow us to calculate the activation energy. Thus the Sum of electronic and zero-point energies = E0 = Eelec + ZPE(zero-point energy)
Since we known that the energy of activation is just the amount of energy require to go from the reactant energy level to the transition state energy level, we can use the corrected electronic and thermal energies we have computed for the transition state and the reactant ro calculate the activation energy by application of the Arrhenius equation. This is simply by taking the difference between the sum of the two energies of the transition state and the reactants to get the energy, then plugging that energy into the equation. A summary of the calculated activation energies are found bellow:
| Transition State Geometry | Activation Energy at 298K using HF/3-21 [kcal/mol] | Activation Energy at 298 K using DFT B3LYP/6-31G(d) [kcal/mol] | Activation Energy at 0 K using HF/3-21 [kcal/mol] | Activation Energy at 0 K using DFT B3LYP/6-31G(d) [kcal/mol] | Experimental Activation Energy at 0 K [kcal/mol] |
|---|---|---|---|---|---|
| Chair | 44.6 | 33.4 | 46.0 | 34.0 | 33.5 ± 0.5 |
| Boat | 55.3 | 41.1 | 55.6 | 42.4 | 44.7 ± 2 |
The activation energies we have generated using Gaussian at 0K at the DFT level agrees very well with experimental values as shown above, almost identical if considering errors in experimentally calculated values. However, the activation energies generated using the HF method shows poor resemblance, with agrees with previous studies that have shown that this method has a poor accuracy in terms of energy, but good with geometry.
It is noted that the activation energy for the boat transition state is higher than that of the chair conformer, which is as expected due to the boat conformer is far more stericly hindered. Thus, the boat transition requires more energy to overcome it activation barrier, and would only react at higher temperatures. thus, kinetic control can be done at lower temperatures for this reaction to become regioselective, with the chair TS dominating. At higher temperatures and longer reaction times, the system well then to react via the boat TS due to thermodynamic control.
Week 2: The Diels Alder Cycloaddition
The purpose of is to study the transition state of two Diels alder reactions, the most prototypical reaction between a cis-butadiene and a ethene molecule and a specific case where both the dieneophile and diene carry substituents. Computational analysis using gaussview allowed for a deep analysis of the HOMO and LUMO of these transition states, of which we can use to predict if that transition state is allowed or not by considering the effectiveness of the HOMO and LOMO overlaps of it's reactants.
Analysis of the π orbital overlaps allows us to observe regiospecficity in more specific reactions with reactants containing substituents, and a analysis of the Exo and Endo transitions state of our second reaction will show a more precise use of gaussveiw to determine regioselectivety base of the effects of substituent on the HOMO and LOMO of the transition states, and thus, the overall energy of the system.
MO study of Cis-Butadiene
AM1 semi-empirical molecular orbital method was used to optimized a molecule of cis-butadiene
The full checkpoint file can be found here
a check of the log file was done to make sure that the energy has converged and the optimization was completed. RMS gradient was check to be close to zero, and it can be concluded that optimization was completed.
| File type | .chk |
| Calculation type | FORT |
| Calculation method | RAM1 |
| Basis set | ZDO |
| Charge | 0 |
| Spin | Singlet |
| Total Energy (a.u.) | 0.04879718 |
| RMS Gradient Norm | 0.00001428 |
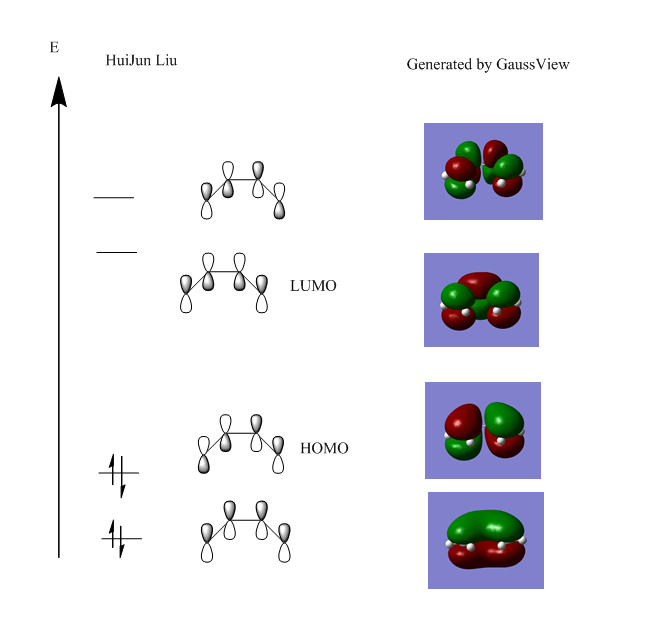
The HOMO and LUMO as well as 2 other corresponding π molecular orbitals were generated on gaussview using the MO function in the Edit bar, and they were compare to theoretical MO generated by LCAO in conventional terms bellow:
As seen, the Gaussian generated MOs corresponds well to the MOs predicted by LCAO theory, suggesting that LCAO approach is quite effective in terms of a molecule like butadiene, and can be use to help predict guess structures of transitions states for the Diels alder reaction in the later parts of this module. The HOMO of the butadiene is antisymmetric with respect to plane and a node is observed between the π orbitals of the two central carbon atoms, suggesting a destabilization of the MO and thus, become the bonding orbital with the highest energy due to this destabilization. The LUMO is an antibonding orbital that is symmetric with respect to plane.
Computation of Transition states of the Prototype Diels Alder Reaction
A guess structure for the transition state of the prototype reaction, takes on a envelope shape and is shown bellow:
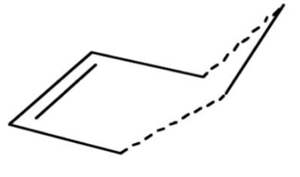
Binary TS Optimization using AM1 basis set
A bicyclo template with a C-C double bond was drawn and a -CH2CH2- fragment fragment was removed to give the guess transition state. The inter fragment distance was 2.2 Å, as found in literature.
The fully optimized log file can be found here
| File type | .chk |
| Calculation type | FREQ |
| Calculation method | RAM1 |
| Basis set | ZDO |
| Charge | 0 |
| Spin | Singlet |
| Total Energy (a.u.) | 0.11165476 |
| Gradient (a.u.) | 0.00002592 |
| Imaginary Freq At | -956.01 |
| Animation of imaginary Freq. | 
|
The log file was check to see that the forces have converged and that the optimization was completed. The RMS gradient also shown to have approached zero to further incline that the optimization was successful. There was only one imaginary frequency of -956.01 cm-1. Thus, tt can be concluded that a transition state was reach and the vibration stretch were as expected. With the formation of the two terminal C-C bonds as well as a stretch along the C=C corresponding to the formation and breakage of this double bond. In all, the lengthening and shortening of bonds in this imaginary vibration was as what is expected to occur during the diels alder reaction.
The imaginary frequency of -956.01 cm-1 is the vibration that corresponds to the reaction path at the transition state and reacts via a synchronous formation of the two sigma C-C bonds between the two terminal carbons. The lowest positive frequency was at 147.27-1 and had a vibration of a slight twist of the two molecules in the transition state. It was clear that it has no contribution the the potential bond forming and breaking during the reaction, and thus, can not correspond to the reaction path.
The Geometry Parameters for the TS is shown bellow:
| Geometry Parameter | AM1 Optimisation |
| C-C Interfragment Bond Length [Å] | 2.119 |
| C-C Bond Length [Å] | 1.383 |
| C=C Bond Length [Å] | 1.398 |
The typical sp3 and sp2 C-C bondlengths and the van der Waals radius of the carbon atom is as follows:
| Bond Type | Length [Å] |
| C-C | 1.54 |
| C=C | 1.35 |
| C van der waals radius | 1.7 |
The calculated C-C interframent bond length is a lot longer than those found in the normal C-C bond, but still shorter than two individual carbon atoms next to each other (two times the van der waals radius). Thus it can be concluded that there is weak interaction between the four terminal atoms during the transition state, but still far from a normal sigma C-C bond. The typical C=C bond in the reactants are slightly shorter than the double bond observed in the transition state while the C-C single bond in the transition state is a lot shorter than normal. Thus it can be concluded that there is a almost even distribution of the 2 pi electron along the four carbon atoms of the butadiene in the transition state.
MO analysis of TS
The computed HOMO and LUMO diagrams are shown bellow:
 |
 |
 |
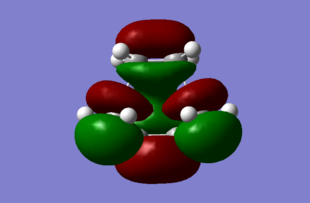The HOMO orbital is asymmetric with respect to plane while the LOMO is symmetric. The HOMO is formed by overlap of the ethene LUMO and the butadiene HOMO orbitals, and is a favorable interaction that allows for the reaction to occur. This is due the fact that ethene is electron-poor, thus it quite happily except electron density into its low lying π* LUMO orbital, while as the butadiene on the other hand, is electron rich with 4 π electrons and quite happily donates it's electron density from its HOMO orbitals. Further more, all the atoms involve in the bonding and forming are carbon atoms, thus they well have very similar energy levels for their AO's which leads to good overlap. The better the overlap, the stronger the bonds. There are several nodes in this HOMO, which slightly destabilies the structure and contributes to the activation energy require to reach the transition state.
The antibonding LUMO is symmetric with respect to plane as stated above, and is form by donation from the ethene HOMO and the butadiene LOMO orbitals. This is a far less favorable interaction and thus, is significantly higher in energy then the HOMO (~200kcal/mol),
Study of Regioselectivity of the Diels Alder Reaction
Exo Transition State
Due to the transition state being a very big molecule, it is not effective to simply optimize it and look at it's energy, thus the frozen coordinates method was applied to get a correct structure for optimization. This method was only applied to the two sigma bonds that formed, and the double bonds were not put through this calculation.
The fully optimized log file via the frozen coordinates methodd can be found here
| File type | .chk |
| Calculation type | FREQ |
| Calculation method | RAM1 |
| Basis set | ZDO |
| Charge | 0 |
| Spin | Singlet |
| Total Energy (a.u.) | -0.05041985 |
| Gradient (a.u.) | 0.00000589 |
| Imaginary Freq At | -812.15 |
| Animation of imaginary Freq. | 
|
A frequency analysis shown only one imaginary frequency with the correct vibration, showing that we have reach a transition state successfully. Close look at the animation of the vibration agree with expected movement of the atoms for the breaking and forming of the bonds during the Diel's Alder reaction. Furthermore, our results shown that the RMS gradient was reasonably close to zero, proving that the energy has indeed converged. Thus it can be concluded that the transition was found successfully.
MO's
 |
 |
 |
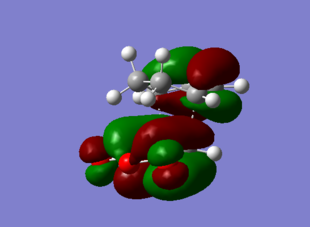
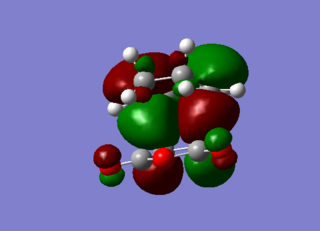The Exo HOMO orbitals is formed from the HOMO of the diene and the LUMO of the dienophile. There is a distinct node in the π bonding orbital of the diene double bond. This shows an absence of secondary orbital overlap effect, or in other words, interaction between the frontier orbitals that are not taking part directly in the bonding. The endo analysis is found below and the conclusion for the secondary orbital overlap effect is there as well.
The LUMO orbitals has distinct nodes in the central fragment, yielding a highly destabilize structure and is clearly antibonding.
Endo Transition State
The fully optimized log file via the frozen coordinates methodd can be found here
| File type | .chk |
| Calculation type | FREQ |
| Calculation method | RAM1 |
| Basis set | ZDO |
| Charge | 0 |
| Spin | Singlet |
| Total Energy (a.u.) | -0.05150479 |
| Gradient (a.u.) | 0.00001074 |
| Imaginary Freq At | -806.36 |
| Animation of imaginary Freq. | 
|
Checks of the gradient and the energy show that energy has converged and the optimization was completed successfully. Only one imaginary frequency was obtained, showing that a TS has been reached. The animation of the vibration agrees with what is expected for the reaction.
It is noted that the Endo TS has a lower energy than the Exo TS, which agrees with previous experimental results.
MO's
 |
 |
 |
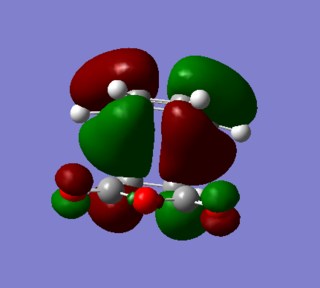A bonding interaction between the frontier orbital of the two carbonyl carbons and the frontier orbitals of the carbon in the butadiene drivative give rise to a secondary orbital overlap effect, which stabilizes the overall transition state. Since this reaction is kinetically driven and the endo product has a lower activation energy due to the stabilization of it's transition state, it can be concluded that the secondary orbital overlap effect is the determining factor for this reaction.
Energies of the two structures
| Type | Exo | Endo |
| electronic energy | -0.05041985 | -0.05150479 |
| Imaginary Frequency | -812.15 | -806.36 |
Our results agrees strongly with what is expected, as it is known for this reaction that the exo transition state should have the higher energy since it is kinetically controlled and thus, the Endo product is favored. Since the Endo TS requires less energy of activation, thus it has a smaller imaginary frequency than that of the exo TS. The Exo form has a higher energy of activation due to the fact that it's more strain in it's TS, this is due to steric clash of the oxygen substituents on the with the aryl substituent on the dienophile, as can be observed with the MO analysis, and bond lengths analysis above.
| Geometry Parameter | Exo | Endo |
| C-C Interfragment Bond Length [Å] | 2.287 | 2.271 |
| C-C Bond Length [Å] | 1.482 | 1.479 |
| C-C Bond Length (Former C=C) [Å] | 1.397 | 1.401 |
| C=C Bond Length (Former C-C) [Å] | 1.401 | 1.402 |
It is observed that the exo and endo has very similar bond lengths with only a slight deviation in the inter-fragment C-C bond distance. It can be seen that a swift and effective moment of electron from the two double bonds to form the two sigma bonds, with a even distribution of electrons across the carbon atoms involve since the C-C bond and the C=C bond that were changed has an identical bond length during the transition state. It is also noted that the typical bond length for a C=C is 1.35 Å, which is very close to our results of the transition state C-C and C=C bonds shown above. There is a large difference observed between the through space a joining molecules between the endo and the exo TS. This is due to steric repulsion of the -(C=O)-O-(C=O)- fragment and the C atoms of the opposite CH2-CH2 for the exo TS and the opposite -CH=CH- of the endo TS, of which the Exo TS experiences more hindered.