Rep:Mod:lh1316
NH3 molecule
Optimization calculation summary
Molecule: NH3 Calculation Method: RB3LYP Basis set: 6-31G(d,p) Final energy E(RB3LYP): -56.55776873 a.u. RMS gradient: 0.00000485 a.u. Point group: C3V N-H bond distance: 1.01798 Å H-N-H bond angle: 105.741°
In order to check whether the job has optimized successfully, we directly looked the file that Gaussian generates. The following information shows forces and displacements are really converged and smaller than threshold. Since they are the gradient of the potential energy curve, zero value of gradient indicates it is in either the ground state or the transition state. The second derivative of the potential energy is k (force constant of the bond) and frequency is proportional to the value of k. The frequency analysis below indicates frequency is positive and thus it is in the minimum energy state and the optimization has completed.
Item Value Threshold Converged? Maximum Force 0.000004 0.000450 YES RMS Force 0.000004 0.000300 YES Maximum Displacement 0.000072 0.001800 YES RMS Displacement 0.000035 0.001200 YES Predicted change in Energy=-5.986278D-10
optimized NH3 molecule |
The optimisation file is liked to here
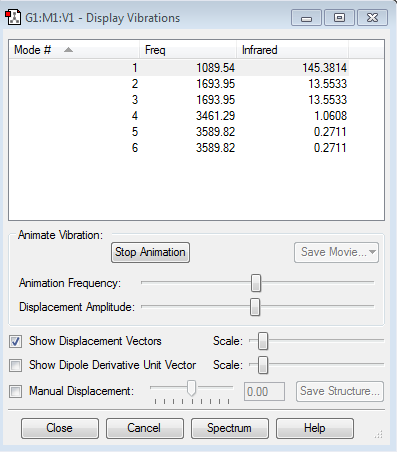
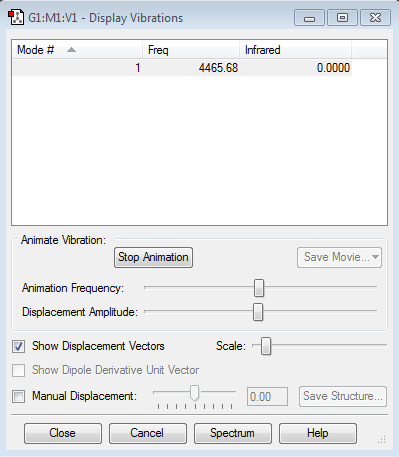
Vibration summary
QUESTIONS & ANSWERS:
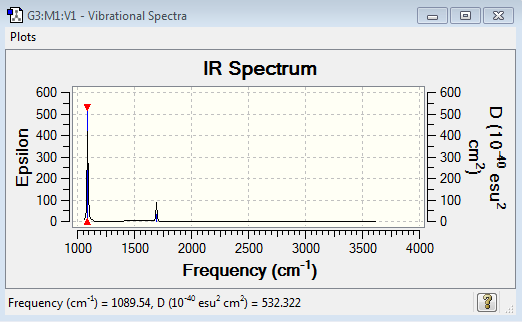
1.how many modes do you expect from the 3N-6 rule? 6 modes. 2.which modes are degenerate (ie have the same energy)? 2 degenerate modes. Mode 2 and 3 are degenerate. Mode 5 and 6 are degenerate. 3.which modes are "bending" vibrations and which are "bond stretch" vibrations? Mode 1,2 and 3 are bending. Mode 4,5 and 6 are bond stretch. 4.which mode is highly symmetric? Mode 1,4 and 6. 5.one mode is known as the "umbrella" mode, which one is this? Mode 1. 6.how many bands would you expect to see in an experimental spectrum of gaseous ammonia? 2 bands. As the vibration picture shows above, mode 4,5 and 6 have small dipole moments and thus leading to small intensities. Their bands would disappear in the noise.
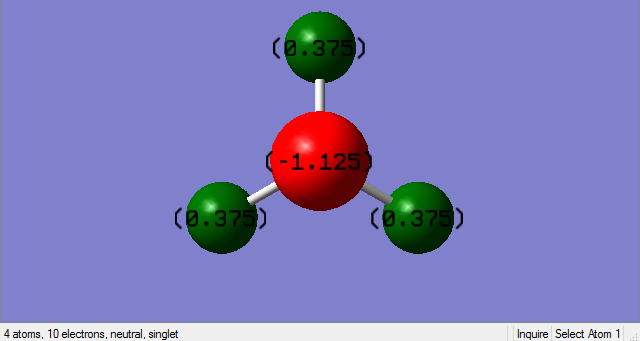
Charge analysis
N-atom should carry negative charge since it is more electronegative and H-atoms should carry positive charge since it is less electronegative.
N2 molecule
Optimization calculation summary
Molecule: N2 Calculation Method: RB3LYP Basis set: 6-31G(d,p) Final energy E(RB3LYP): -109.52412868 a.u. RMS gradient: 0.00000060 a.u. Point group: D*H N-N bond distance: 1.10550 Å
The information in the table below shows forces and displacements are really converged and the optimization has completed.
Item Value Threshold Converged? Maximum Force 0.000001 0.000450 YES RMS Force 0.000001 0.000300 YES Maximum Displacement 0.000000 0.001800 YES RMS Displacement 0.000000 0.001200 YES Predicted change in Energy=-3.401090D-13
optimized N2 molecule |
The optimisation file is liked to here
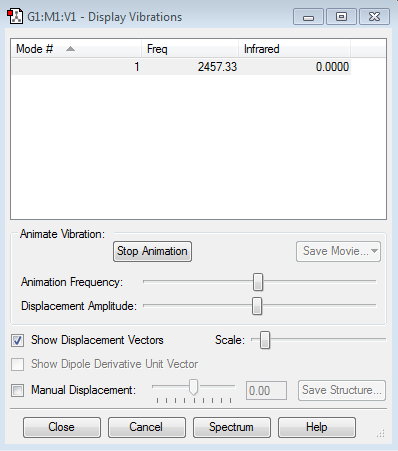
Vibration summary
There is no bands in the spectrum because N2 is symmetric and do not have change in the dipole moment.
H2 molecule
Optimization calculation summary
Molecule: H2 Calculation Method: RB3LYP Basis set: 6-31G(d,p) Final energy E(RB3LYP): -1.17853936 a.u. RMS gradient: 0.00000017 a.u. Point group: D*H H-H bond distance: 0.74279 Å
The information in the table below shows forces and displacements are really converged and the optimization of H2 molecule has completed.
Item Value Threshold Converged? Maximum Force 0.000000 0.000450 YES RMS Force 0.000000 0.000300 YES Maximum Displacement 0.000000 0.001800 YES RMS Displacement 0.000001 0.001200 YES Predicted change in Energy=-1.164080D-13
optimized H2 molecule |
The optimisation file is liked to here
Vibration summary
The frequency of H2 vibration is greater than that of N2 vibration because the frequency is related to the (k) force constant of the bond and (μ) reduced mass. The greater the mass, the lower the vibration frequency. Hence, H2 has greater vibration frequency.
Haber-Bosch reaction energy calculation
N2+ 3H2 -> 2NH3 E(NH3)= -56.55776873 a.u. 2*E(NH3)= -113.11553746 a.u. E(N2)= -109.52412868 a.u. E(H2)= -1.17853936 a.u. 3*E(H2)= -3.53561808 a.u. ΔE=2*E(NH3)-[E(N2)+3*E(H2)]= -0.0557909 a.u. = -146.47848285 kJ/mol
The enthalpy change of formation of NH3 is -73.24 kJ/mol. Since the reaction is exothermic, the ammonia product is more stable than the gaseous reactants.
The literature value of the energy change is -92.0kJ/mol.[1]
We used the optimized structure to calculate the reaction energy hence it is common to have difference between theoretical and practical value.
Choice of small molecule (ClF3)
Optimization calculation summary
Molecule: ClF3 Calculation Method: RB3LYP Basis set: 6-31G(d,p) Final energy E(RB3LYP): -759.46531688 a.u. RMS gradient: 0.00002465 a.u. Point group: C3V Cl-F bond distance (equatorial): 1.65143 Å Cl-F bond distance (axial): 1.72863 Å F-Cl-F bond angle (equatorial-axial): 87.140° F-Cl-F bond angle (axial-axial):174.281°
The information in the table below shows forces and displacements are really converged and the optimization of H2 molecule has completed.
Item Value Threshold Converged? Maximum Force 0.000050 0.000450 YES RMS Force 0.000028 0.000300 YES Maximum Displacement 0.000204 0.001800 YES RMS Displacement 0.000134 0.001200 YES Predicted change in Energy=-1.250218D-08
optimized CLF3 molecule |
The optimisation file is liked to here
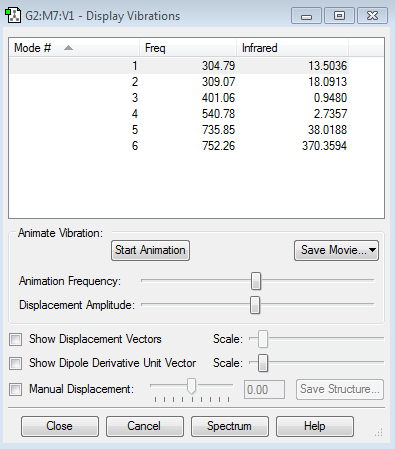
Vibration summary
Vibrational modes 1 and 2 are degenerate modes. But the frequency is a little different because of the imperfect T-shape structure of ClF3.
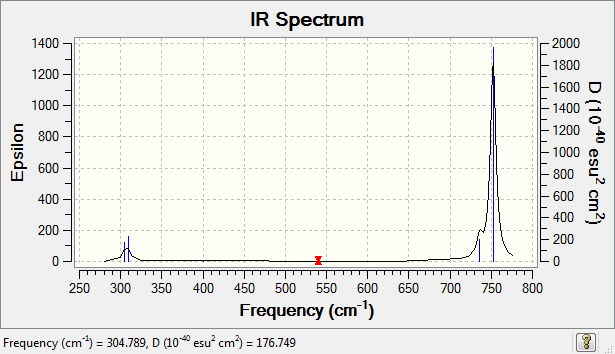
There are 3 bands in the spectrum. The vibration frequencies are low because of heavier F and Cl atoms. As the vibration picture shows above, mode 3 and 4 have small dipole moments and thus leading to small intensities. Thus their bands would disappear in the noise. Since the intensities of mode 1 and 2 are extremely close, only one peak appears.
Charge analysis
Cl-atom carrys positive charge since it is less electronegative and F-atoms carry negative charge since they are more electronegative. F atoms have different charges due to different molecular orbitals overlapped with Cl atom.
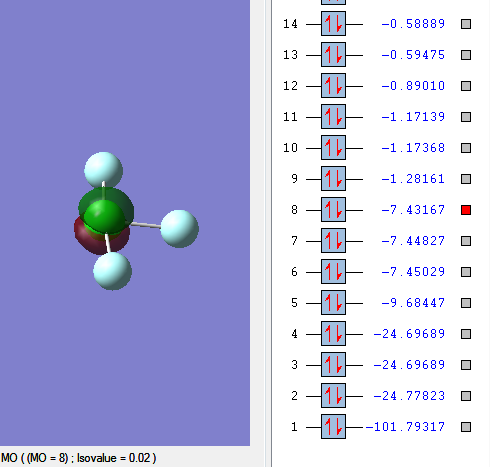
Molecular orbitals
2p orbital of Cl
MO7, 8 and 9 are formed by degenerate 2p orbitals of Cl atoms.
The small difference in energy is due to different orientation and hence different repulsion with F atom.
Occupied MO bonding
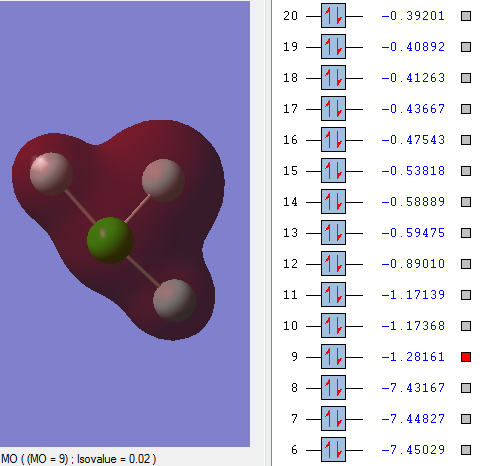
MO9 is the sigma bonding between one 3s orbital of Cl atom and three 2s orbital of F atoms.
The enegy of MO9 is 6.2 a.u. higher than that of MO8 because MO8 is non-bonding and the electrons are held tightly to the respective nuclei.
Occupied MO mixture
One 3s orbital of Cl atom and two 2s orbital of F atoms in MO10 form sigma bonding.
The 2s orbital of equatorial F atom is out of phase with the left three atoms.
The energy of MO10 is 0.11 a.u. higher than that of bonding MO9.
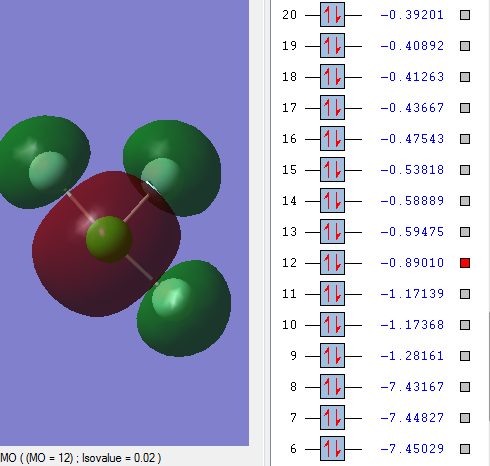
Occupied MO antibonding
In MO12, The 3s orbital of Cl atom is out of phase with all three 2s orbital of F atoms.
MO12 is higher in energy than the bonding MO9. The energy difference between the bonding and antibonding orbitals is much larger because they overlap better. These are valence orbitals and they are very involved in the chemical bonding.
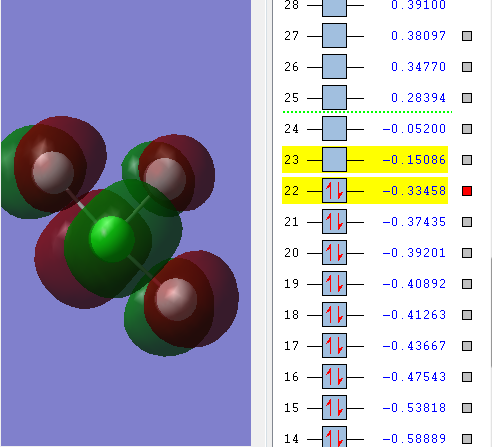
Occupied MO antibonding
In MO22, 3p orbital of Cl atom is out of phase with 2p orbitals of all three F atoms.
MO 22 is HOMO(highest occupied molecular orbital).
Haber-Bosch reaction energy calculation
Cl2 + 3F2 -> 2ClF3 E(ClF3)= -759.46531688 a.u. 2*E(ClF3)= -1518.93063376 a.u. E(Cl2)= -920.34987886 au E(F2)= -199.49825218a.u. 3*E(F2)= -598.49475654 a.u. ΔE=2*E(ClF3)-[E(Cl2)+3*E(F2)]= -0.08599836 a.u. = -225.79 kJ/mol
The enthalpy change of formation of ClF3 is -112.89 kJ/mol. Since the reaction is exothermic, the product ClF3 is more stable than gaseous reactants.