Rep:Mod:lh106module2

BH3 Introduction Module

A molecule of BH₃ was created and optimised using Gaussian with the B3LYP method and a 3-21G base set (so quite a rough approximation to start with)to give the optimised molecule. The B3LYP method is a combinatin of the Lee, Yang and Parr correction that was created to fit the helium atom and B3 hybrid exchange function. It is therefore definitely an approximation as it only accurately fits helium.

BCl

Optimised B-H bond distance	1.5A
Optimised H-B-H angle	120°
File type	.log
Calculation type	SP
Calculation method	RB3LYP
Base set	3-21G
Final energy	-26.38297143au
Dipole moment	0 Debye
Point group	D3H
Length of time	10 seconds

From this optimised molecule, the overall energy could be observed:

Vibrational Modes
The vibrational modes of BH₃ were also calculated using Gaussian. Gaussian was also used to visualise the vibrational modes

BH₃ Infrared Spectrum

No.	Form of Vibration	Frequency	Intensity	Symmetry D3H point group
1		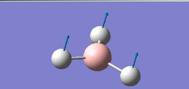1145.71	92.6991	A1”
2		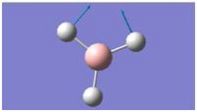1204.66	12.3789	E’
3		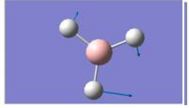1204.66	12.3814	E’
4		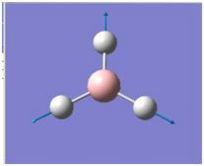2592.79	0	A1’
5		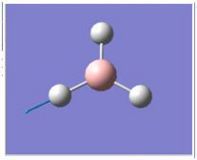2731.31	103.837	E”
6		2731.31	103.83	E”

Molecular Orbitals
Gaussian was also used to observe the molecular orbitals in the BH₃ molecule. Firstly a MO diagram was created for the molecule: The Molecular orbitals for the occupied orbitals and LUMO were calculated
HOMO (1e'):
LUMO(1a"₂:
Orbital 1(:
Orbital 2:
Orbital 3:
Orbital 4: The HOMO and LUMO compare well to their qualitative counterparts. The LUMO should look like the unpaired p orbital and does. Orbital 1 refers to the 1s orbital not shown in the molecular orbital diagram as it is too low in energy, orbital 2 should also refer to this energy level. Orbital 3 doesn't look quite right as I would expect to see some of the boron orbital but this could be because the boron orbital is encased in the hydrogen s orbitals.

BCl₃

The same optimisation was run for BCl₃ so that the differences between it and BH₃ could be explored. This gave the same information as before:

Optimised B-H bond distance	1.86592A
Optimised H-B-H angle	120°
File type	.log
Calculation type	FOPT
Calculation method	RB3LYP
Base set	LANL2MB
Final energy	-69.43928112au
Dipole moment	0.00005905 Debye
Point group	D3H
Length of time	13 seconds

This molecule took a few seconds longer to calculate, probably because it is a slightly bigger molecule. The final energy and the optimised bond distance were greater in BCl₃ than in BH₃. This is because a greater dipole moment is created and a large molecule has been added (the chlorine) and so can not sit as closely to the Boron.

Small Molecule- H₂O₂

The method learnt from optimising BCl₃ and BH₃ was put into practice on another small molecule-H₂O₂.

Optimised H-O bond distance	1.03771A
Optimised O-O bond distance	1.47299A
Optimised H-O-O angle	97.002°
File type	.log
Calculation type	FOPT
Calculation method	RB3LYP
Base set	LANL2MB
Final energy	-149.45059613au
Dipole moment	0.0003 Debye
Point group	C2
Length of time	37 seconds

The coordinates for this optimisation were as follows:

Centre Number	Atomic Number	Atomic Type	Coordinates (Angstroms)
			X	Y	Z
1	8	0	0.000000	0.000000	0.000000
2	1	0	0.000000	0.000000	0.960000
3	8	0	1.244287	0.000000	-0.440625
4	1	0	1.244287	-0.000175	-1.400625

Cis vs Trans Isomer

The cis and trans forms of the molecule Mo(CO)₄₍PPh₃)₂ were optimised using increasingly more accurate basis sets and pseudo-potentials do give a more accurate geometry optimisation.

The B3LYP Method with LANL2MB pseudo-potential was used to give a rough optimisation and then the same method but with a LANL2DZ pseudo-potential was used to give a more accurate optimisation.

Trans Structure

Trans structure

Trans Optimised Bond Lengths and Angles

Distance/angle	Experimental	LANL2DZ Pseudo-Potential	Literature
Mo-C	1.98571 A	2.0299 A	2.016 A
C=O	1.20328 A	1.1874	1.164 A
Mo-P	2.81901 A	2.61873	2.500 A
P-Ph	1.96335 A	1.897, 1.894, 1.892	1.854 A
P-Mo-C	91.592°	114.9, 117.4, 116.3	87.2°
C-Mo-C	86.948°	179.835	180° and 92.1°
Mo-P-Ph	108.625°, 126.095° and 117.426	114.876, 116.283, 117.378
Ph-P-Ph	102.4°, 98.257°	103.456, 100.653

Cis Isomer

Transstructure

Cis Optimised Bond Lengths and Angles

Distance/angle	LANDL2MB Pseudo-Potential	LANL2DZ Pseudo-Potential	Literature
Mo-C	2.04592 A	1.97156 A	2.007 A
C=O	1.20367 A	1.19118 A
Mo-P	2.68694 A	2.73616, 2.76 A	2.576, 2.577 A
P-Ph	1.9673 A	1.89 A
P-Mo-C	88.209°	91.794°	92.1°
C-Mo-C	179.885° and 89.736°	175.173° and 86.098°	92.1°
Mo-P-Ph	116.562°	122.431
Ph-P-Ph	100.206°	97.664

The main difference between the cis and the trans isomers is the in the angles because of the different configurations.

Also obtained from the Gaussian calculations is the energy of each isomer;

Isomer	Energy, au
Cis	-1923.54175254
Trans	-1923.54028665

This shows that cis form is slightly more stable, this could be because the large PPh₃ groups are further away from each other than in the cis isomer. Therefore there is less strain from these large groups. If there were a smaller group, for example a methyl group,instead of the bulky PPh₃ then this would lower the strain that would occur in both isomers. If there still needed to be the bulky groups, the phenyl groups on the PPh₃ could be adjusted. From the Gaussian calculation, the phenyl groups are orientated in a "windmill-like" configuration, this keeps the phenyl groups away from each other, thus reducing strain but can result in the phenyls being in conflict with other groups. The seperate phenyls could be adjusted slightly to minimise strain from both other groups in the PPh₃ and the other groups in the complex.

Vibrational Frequencies The vibrational frequencies were calculated using the frequency function in Gaussian. The cis molecule gave some negative frequencies which the trans did not. Also, the cis molecule was expected to give 4 C=O stretches as opposed to only 3 in the trans form. This is as a result of four different vibrations in the molecule- asymmetric stretching and symmetric stretching of the two groups.

Cis Isomer

Calculation, cm-1	Literature, cm-1
1847.77	1882
1851.31	1903
1875	1917
1966	2022

Trans Isomer From literature it was predicted that there would be only 3 C=O stretches, probably due there being PPh₃ groups in only one plane- the trans position.

Calculation, cm-1

1842.81

1845.65

1890.65

1959(very low intensity)

There are 4 peaks, but the last peak is at a very low intensity, this corresponded to the symmetric stretch

Inversion of Ammonia

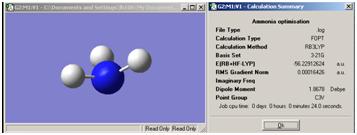
First, a model of ammonia was created and optimised.

Another model was made with one N-H bond being 1.01A long rather than 1A. This changes the symmetry of the molecule from C3V to C1

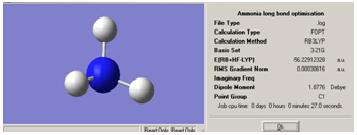
Another model with D3H symmetry was optimised using the same method:

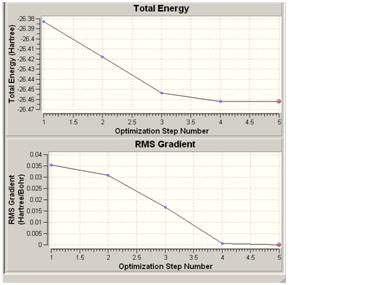
The structure of the D3H molecule differed from the other two in that the H-N-H angle was 120° as opposed to 110° in the other symmetries. This is to fit in the D3H symmetry model. The symmetry of the molecule also had an effect on the time taken to optimise the geometry. The more the molecule was altered from the original C3V model, the longer it took for the calculation to run. This suggests that the symmetry closest to the real situation is the quickest to optimise and so will give the quickest calculation time. Normally the molecule cannot break symmetry during an optimisation but, especially in the case of high symmetry molecules, the symmetry can be "turned off". This inability to break symmetry has ramifications for highly symmetrical molecules as they may need to break symmetry. If they cannot, the most optimised form may not be found.

The lowest energy geometry was for the D3H symmetry optimisation with -56.53154189 au. Although all three geometries gave very similar energies as they are effectively the same molecule. The energies for the other isomers are as follows: C3V= -2.14165496E-2KJ/mol-1, C1=-2.14165485E-2KJ/mol-1. Hence the difference between these energies and the lowest D3H energy can be calculated as:C3V= 1.1518407E-4, C1=1.1518520E-4. This difference does seem small but could still be significant.

The C3V and D3H models were optimised further using the 6-311+G(d,p) basis set so that the inversion of ammonia could be observed.

The calculations using this basis set took longer than for its lower level counterpart. This is probably because this is a more accurate calculation and hence requires more time to complete.

The change in energy between the C3V and D3H geometries was calculated (the process of the inversion). This was found to be 2.96934E-6. The ΔE value has therefore been reduced between the two basis sets by the use of a more accurate basis set. These results are a lot lower than the expeirmentally determined barrier of 24.3 KJ/mol, this could be because the computational method gives a more accurate value.

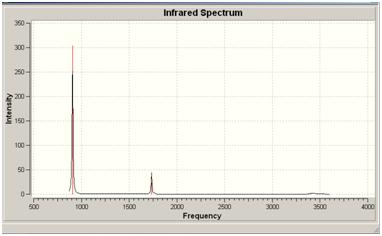
Ammonia Vibrational Frequencies
The frequencies of the C3V and D3H models were calculated using gaussian and compared.

C3V

C3V	Calculated		Literature	Matched up?	D3H	Calculated
Frequency	Intensity	Frequency	Intensity		Frequency	Intensity
906.325	303.409	1139	1	Yes	-318.051	849.113
1734.71	22.6457	1765	1.1E-6	Yes	1640.59	55.9805
1734.71	22.6456	1765	1.1E-6	Yes	1640.59	55.9828
3401.89	2.1217	3464	0.073	Yes	3635.71	0
3566.88	0.0635	3534	0.052	Yes	3854.27	19.5963
3566.88	0.0634	3646	0.073	Yes	3854.71	19.5951

The C3H geometry gave 6 positive frequencies with two pairs of degenerate levels. The D3H isomer gave only 5 positive frequencies, again with two degenerate pairs. As the D3H structure is a transition state it has a negative frequency, this occured at -318.051 whereas the C3V,being a ground state structure does not have this and only has positive frequencies.

The first vibrational mode (pictured below) follows the reaction path as it stays the same for both symmetries.