Rep:Mod:lesmizphan1
Molecular Mechanics Modelling
Hydrogenation of Cyclopentadiene Dimer
Dimerisation of Cyclopentadiene
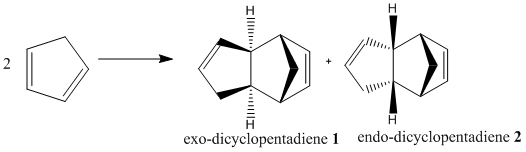
Cyclopentadiene is known and shown to dimerise at room temperature, via Diels Alder mechanism, to form two possibilities of dicyclopentadiene -- an exo dimer 1 or an endo dimer 2, though experimentally only endo dimer 2 has been observed.
The relative energies of dimers 1 and 2 are compared by geometry optimisation with MM2 method on ChemBio3D-11.0.
Exo-dimer 1
Structure 1 |
Endo-dimer 2
Structure 2 |

Dimer 1 has a lower total energy (133.4 kJ/mol) than dimer 2 (142.3 kJ/mol), indicating the former being the thermodynamic favourable product of the dimerization, in agreement with prior literature findings[1] that the exo-isomer is the more stable outcome. In contrast, the dimer higher in energy is formed as a kinetically favourable product, formed via a low-energy transition state. It is confirmed by the selection rule put forward by Woodward-Hoffman[2], and Alder's endo-rule [3], that endo-selectivity is favoured. And since Diels Alder's reaction is irreversible, the kinetic product dominates, and hence the endo dimer 2 is observed instead of the more energetically stable exo-dimer 1.
Hydrogenation of Dicyclopentadiene
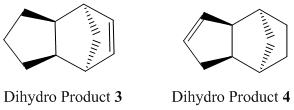
Upon hydrogenation of endo dimer 2, dihydro products 3 or 4 could form, as shown below:
Dihydro Product 3
Structure 3 |
Dihydro Product 4
Structure 4 |

Product 4 has relatively lower energy than product 3 (130.4 kJ/mol compared to 150.3 kJ/mol), thus product 4 is known to be thermodynamically stable product, i.e. its double bond in the 6-membered ring is more easily hydrogenated than that in the 5-membered ring. This is echoed by findings in literature[4] -- where endo-dicyclopentadiene is hydrogenated to 4 before complete reduction upon prolonged period of time.
The major difference between the energy contributions of dihydro 3 and 4 is bending energy -- product3 has a larger bending contribution than 4, by nearly 20kJ/mol. This is due to the higher bond and angle strain experienced by dihydro derivative 3 (bond angle ~108°), having a double bond in the five-membered ring with a bridge, straining the system which becomes more rigid. In contast, derivative 4 has a more flexible 5-membered ring with a bridge (without any C=C constraints), with the double bond being in the 6-membered ring which does not affect the overall system much. And thus, strain is released from the system. Its bond angle is ~113°, closer to the ideal sp2 120° angle. Whereas the bond angle in 3 is about 108°, deviating much more from the ideal 120°. Hence, these rationalisation explains the lower bending energy and stability of dihydro derivative 4.
Stereochemistry of Nucleophilic additions to a pyridinium ring
N-Methyl Pyridoxazepinone with Grignard Reagent
N-methyl pyridoxazepinone 5 undergoes nucleophilic addition (reaction scheme shown below), by nucleophilic Grignard reagent methyl magnesium iodide which alkylates the pyridine ring at the C4 position, leading to highly selective product 6 [5].
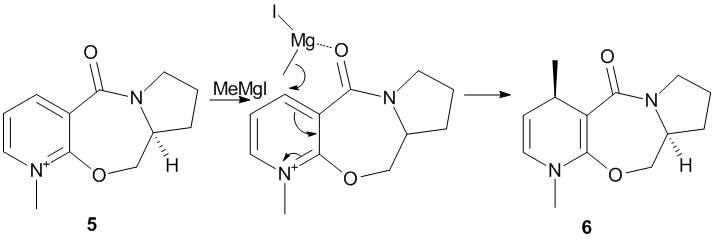
It is not possible to view the interaction of compound 5 with MeMgI in ChemBio3D due to the element Magnesium not recorded/not recognized in the programme. However, it is known from Schultz et al[6] that the incoming Grignard reagent coordinates to the electronegative carbonyl oxygen, due to Mg being electropositive, thus spatially facilitating the attack of nucleophile Me- anion to the C4 position on pyridine ring. It is illustrated by the transition state structure in the above reaction scheme. Hence, it is necessary to know the geometry of carbonyl group, if it is above or below the plane of the rings, which in turn determines the position of nucleophilic attack and hence dictates the geometry and stereochemistry of final product.
An analysis of the dihedral angle (between the C=O and the pyridine ring) was performed by geometry minimization with MM2 method on ChemBio3D-11.0. (Note to marker: The short calculations have been done on my personal computer, which has the old version of 11.0, thus no "bug" problems with N+ was experienced) The dihedral angle was fixed and the optimized energy was recorded, as shown in Graph 1.

From these analyses, it is apparent that the minimum energy conformation occurs when the dihedral angle between the carbonyl C=O and the pyridine ring is 24° above the plane of the ring. It is further noted that it does not reach a low energy conformation when C=O is below the plane of ring (i.e. negative dihedral angle). The incoming Grignard coordinates to the electronegative carbonyl oxygen (as illustrated by reaction scheme) above the plane of ring, due to C=O being above the ring, leading to nucleophilic addition occurring at the top of the ring at the C4 position of the pyridine. Hence, it results in the product 6 having the geometry of methyl group above the plane of the ring.
The geometrically optimized jmol molecule 5 can be viewed as well by clicking the button below.
N-methyl Quinolinium Salt with Aniline
Again, N-methyl quinolinium salt 7 reacts with aniline in a nucleophilic addition reaction, but without any coordination of the nucleophile to the carbonyl (unlike with compound 5). The reaction mechanism is shown here:
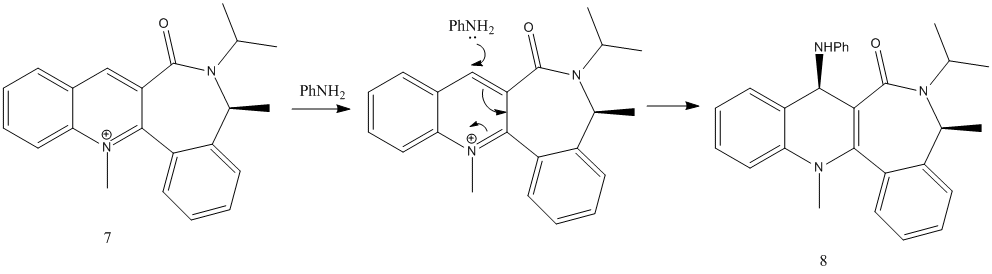
Similarly, a relationship between the dihedral angle (between carbonyl C=O and the conjugated aromatic rings)and their corresponding relative energies was investigated. Results are shown in table 4 and graph 2 below:
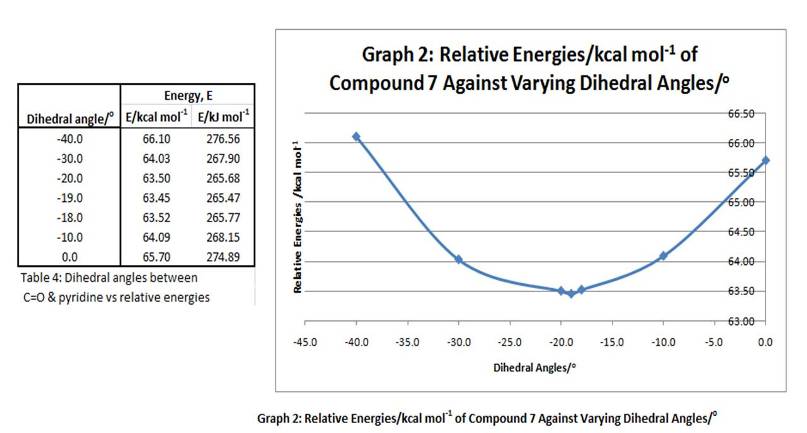
From here, it can be seen that the most stable (minimum energy) conformation occurs at a dihedral angle of -19°, with C=O below the plane of the rings. Again, no stable conformations was found with C=O above plane of rings. With such a steric barrier below the rings, the nucleophile aniline would approach the C4 position and add the methyl group from the top. Hence, it leads to the resulting stereochemistry of product 8, with the added Me group above plane of rings.
This rationalisation and calculations are in sync with findings reported by Leleu et al[7], that due to steric control, the incoming nucleophile reacts on the opposite face from the carbonyl group.
The geometrically optimized molecule 7 jmol can be viewed from this button:
Possible Improvements
MM2 (or MMFF94) is a purely mechanical molecular model, while MOPAC would be an improvement as it shows electronic aspects of reactivity. A more thorough and intensive mode of calculation would be to use Gaussian DFT. Also, a system with recorded elements like Mg would be useful as it would help visualise and predict the energy changes as nucleophilic Grignard approaches and coordinates to derivative 5.
Intermediate in the Synthesis of Taxol
In the synthesis of the drug Taxol, intermediates 9 and 10, shown below together with jmol presentations, are key structures with high alkene stability. On standing, the compound isomerises between 9 and 10, which are alternative carbonyl isomers, with C=O either pointing up or down, forming atropisomers with chirality about the axis.
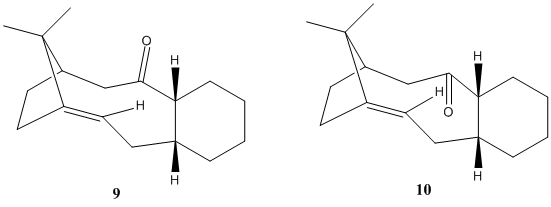
The energetic stability of these two structures are analysed using Chem3D 11.0, by the MM2 method, and the results are shown below in table 5. MMFF94, another molecular mechanical modelling method more suitable for modelling biological systems was tried out, and the trend of results follow as MM2, though absolute values are higher by ~10-20kcal/mol.(results not shown).

As shown from the analysis, Intermediate 9 is less energetically favourable, having adopted a twist-boat cyclohexane conformation with C=O pointing up. The favourable staibilising σ-π* conjugation between σ(C-H) and π*(C=O) interactions is offset and upset by the larger transnnular strain between the C=O and other H's point upward, rendering the overall system as unfavourable and less stable (total energy 226 kJ/mol). On the other hand, the more energetically favourable intermediate 10 adopts a more stable chair cyclohexane conformation, and the C=O points downward, away from steric constraints posed by neighbouring hydrogens pointing upward. The release of the steric strain makes intermediate 10 the lower-energy conformation (185 kJ/mol). These are in agreement with literature findings[8], where the intermediate spontaneously isomerizes to structure 10.
Hyperstable alkene, i.e. extra stable bridgehead alkenes, is seen here in these two bicyclic systems, as was reported by McEwent et al[9]. The negative olefin strain energies (i.e. less strained) on the hyperstable olefins can lower thermodynamic driving forces of the reaction, and thus the structure of lowest olefin strain would have the trans-cycloalkene in the bigger ring.
Due to the steric hindrance that inhibits incoming reactants, these hyperstable olefins react less readily and slowly, allowing other groups to be reduced while leaving these alkenes untouched in the synthesis of Taxol[10].
Modelling Using Semi-empirical Molecular Orbital Theory
Regioselective Addition of Dichlorocarbene
Orbital Control of Reactivity
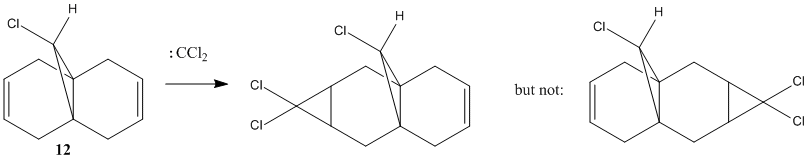
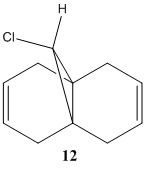
The reaction scheme below shows the reaction of 9-Chloro-1,4,5,8-tetrahydro-4a,8a-methanonaphthalene 12 and dichlorocarbene, which adds to the syn alkene C=C and leading to the endo product. It does not add to the anti C=C and thus no exo product is observed.[11] This result is rationalised by molecular orbital analysis, done by MOPAC/PM6 on Chembio3D-11.0.
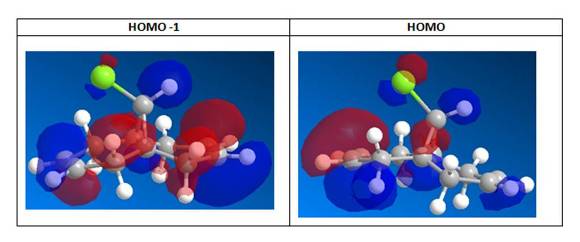
From the figures of HOMO shown, it can be seen that a far larger electron cloud resides over the syn C=C bond (i.e. the C=C nearer to the Cl) than anti C=C, rendering syn C=C much more nuleophilic. The presence the proximal electronegative Cl, which is electron-withdrawing in nature, further adds electron density to this side of the compound, adding to the nucleophilicity of the syn C=C. Hence, the syn C=C is more susceptible to electrophilic attack from CCl2 carbene, resulting in the major endo product (72%) and not the exo (present only in minor amount, 23%)[11] .
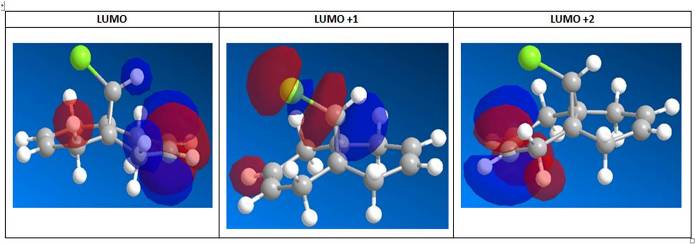
From the LUMO figures, the LUMO and LUMO+2 are π* orbitals while LUMO+1 is the the C-Cl σ* orbital. LUMO+1 σ*(C-Cl) interacts with HOMO-1 π(C=C) of the anti-alkene orbital, to show an antiperiplanar stabilisation. It thus agrees literature[12] that the σ*(C-Cl) interacts with the π(C=C) to lead to a stabilising interaction that lowers the energy of the molecular orbitals for anti-alkene, which ultimately lead to a more reactive syn-alkene. It is to be noted that the Rzepa et al[12] used the PM3 method of MOPAC instead of the PM6 employed here in this experiment, thus explains the differences in shapes and structures of the molecular orbitals. However, it is observed that the general trend of electron density and direction of electron clouds are similar, and thus makes a relevant comparison with values obtained in this experiment.
Vibrational Frequencies
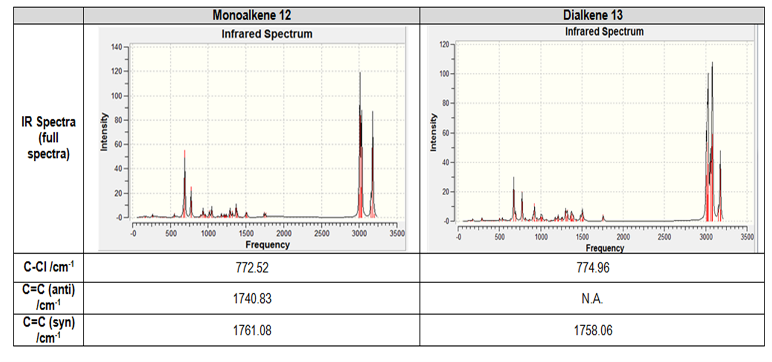
The influence of C-Cl bond on C=C infrared (IR) vibrational frequency is investigated in compound 12 and its hydrogenated form, the monoalkene 13, where only the anti-C=C is reduced while retaining syn C=C. Using Gaussian geometry optimisation and B3LYP/6-31G(d,p) modelling, their respective IR frequencies are recorded as follow in table 6:
Table 6: Comparison of IR values between dialkene 12 and monoalkene 13.
Data for compound 12: DOI:10042/to-5650
Data for compound 13: DOI:10042/to-5649
The general full spectra of these compounds are shown above in the table -- their spectra look similar, due to the same functional groups present in both. A closer look is taken at key functional groups, C-Cl bonds and C=C(syn) and/or C=C(anti), and their differences are apparent. Both C-Cl vibration frequency values (773 and 775cm-1 respectively) correspond closely to reported data of 780cm-1[13]. In dialkene 12 two C=C are present, having two IR peaks at 1741cm-1 (anti) and 1761cm-1 (syn). In monoalkene 13, only one syn C=C is present, thus the peak at 1758cm-1. No recorded IR spectrum of these two compounds was found from literature; but general IR knowledge usually accepts a typical value of around 1600-1700cm-1 for alkene bonds[13]. Therefore, C=C frequencies in compounds 12 and 13 are higher than normal, most likely due to the influence of the nearby electronegative Cl. From the LUMO digrams above, the antiperiplanar stabilisation caused by the favourable interaction of σ*(C-Cl) with the π(C=C), which lowers the energy of the anti-alkene π orbital, ultimatively leading to a stronger bond and higher vibration frequency than usual. Similarly, such orbital interactions exist for syn-alkene, resulting in its stabilisation than the usual C=C.
Anti C=C is seen to have lower stretching frequency than syn C=C, implying the former being a weaker bond (i.e. easier to break/react). This might explain the reason for hydrogenating only the anti C=C and not syn C=C, but it contradicts prior findings from MO analysis, where HOMO orbital is shown to favour the reactivity of syn C=C with dichlorocarbene. This discrepency could have resulted from inherent limitations posed by the computational modelling used. Another modelling method perhaps would lead to a different result.
Structure-Based Mini-Project
Introduction: Diels Alder Enantioselectivity
The Diels-Alder reaction between cyclopentadiene and cinnamaldehyde, catalysed by amine derivatives (NHR2.HCl), as documented by Ahrendt et al[14] is investigated in this structure-based section. The endo/exo selectivty (enantioselectivity) of this reaction is illustrated in the scheme below, with preference over endo-product -- endo:exo 1.3-2.6:1 depending on catalyst used.
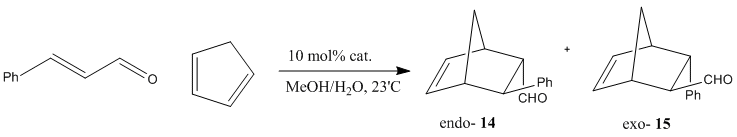

Catalyst structure diagram taken from reference by Ahrendt et al[14]
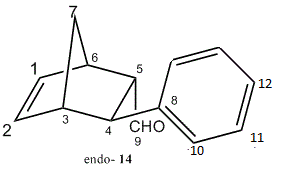
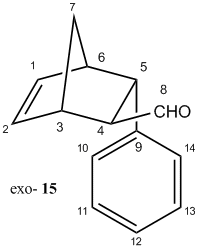
Computational modelling and calculations were employed to differentiate spectroscopically between the enantiomeric products, namely, (1S,2R,3R,4R)-3-Phenylbicyclo[2,2,1]hept-5-ene-2-carboxaldehyde as the endo product (14) and (1R,2R,3R,4S)-3-Phenylbicyclo[2,2,1]hept-5-ene-2-carboxaldehyde as the exo product (15).
Mechanistic Analysis
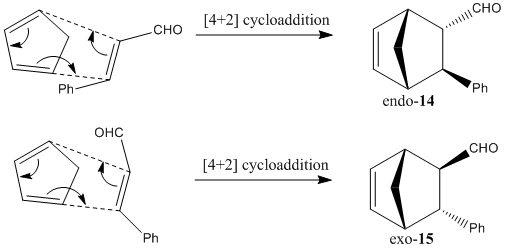
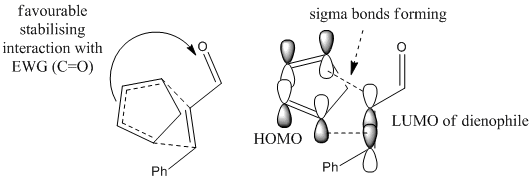
The mechanisms above shows the pathways of endo- and exo- products formation. As mentioned in the first part of this module under cyclopentadiene dimerization (Diels Alder reaction), endo selection rule usually applies, favouring endo products formation. It can be explained by frontier orbital interactions. In the transition state models commonly proposed (shown below), while new σ-bonds form between HOMO of electron-rich diene (cyclopentadiene) and LUMO of electron-deficient dienophile (cinnamaldehyde) due to compatible symmetry and phase, a favourable stabilising interaction is also occuring at the back of the diene, where the forming pi-bond forms bonding interaction with electron-withdrawing carbonyl group. This conformation stabilises the energy of the transition state, and hence encourages the formation of endo product.[15]
Both products, it is to be noted, adopt the A1,3 eclipsed conformation, and its steric repulsions experienced by the axial components (between lone pair on C=O and C-H bond) is minimized by the favourable interaction betweenσ(C-H) and π*(C=O). Upon geometry optimization by MM2, the relative energy calculated for endo and exo products are predicted to be 30.79 and 32.91 kcal/mol respectively. It indicates that endo product is slightly more energetically stable, i.e. interaction between σ(C-H) and π*(C=O) is more favourable.
13C NMR
Spectroscopic methods were used to attempt differentiating the endo (14) and exo (15) products below. Since both products exhibit exactly the same functional groups, thus IR spectrum would not be useful to tell them apart. 13C NMR was calculated, using Gaussian mpw1pw91/6-31(d,p), and the results are shown in the table below, along with literature values[14] for comparison.
Data for endo 14:DOI:10042/to-5656
Data for exo 15:DOI:10042/to-5655
The NMR spectra demonstrate extreme similarities, and the assignments and values correspond to literature very well. The slight differences between predicted and literature values (not more than 4ppm) could be due to inherent limitations of the computational method, creating a simulated real-life molecule and environment/solvent. But it provides reliable enough a trend to agree with literature. The vast extent of similarities make differentiation hard, though not impossible through the small differences in values when two isomers are compared. However, if given any one unknown enantiomer, it would be impossible to tell which product it is.
Optical Rotation
Since IR and NMR could not provide enough information, optical rotation was tried. Under real synthesis environment, this could only be done after the racemic mixture of enantiomers are separated by physical means -- from literature, both enantiomeric excess can achieve up to 93% ee[14] .
Again, the calculation was performed on Gaussian mpw1pw91/6-31(d,p). The optical rotation [α] obtained was -176.0° for exo product 15 and -90.2° for endo product 14. Unfortunately, optical rotation data has not been experimentally determined or recorded in past literature, but it seems a promising way to differentiate and identify the isomers.
Conclusion
In this particular example of Diels Alder stereoselectivity, IR and NMR spectra prediction using computational analysis yields useful results that agree with literature records, and further usage of optical rotation analysis can provide meaningful differentiation between the stereoisomeric products though literature documentation does not exist. This example provides meaningful evidence that computational DFT-based MO modelling can aid organic synthesis, in terms of predicting products through geometrical and energetical means, and predict properties through spectroscopic means (IR, NMR, etc).
Prior exercises before the mini project also provide ample evidence that molecular mechanics and semi-empirical molecular orbital theory are useful tools in organic synthesis prediction/hypothesis, as they yield results comparable to literature empirical findings.
References
- ↑ W.C. Herndon, C.R. Grayson, J.M. Manion, J. Am. Chem. Soc.., 2002, 124, 1130: DOI:10.1021/jo01278a003
- ↑ R. Hoffman, R. Woodward, J. Chem. Soc., 1965, 87, 4388-4389: DOI:10.1021/ja00947a033
- ↑ K. Alder, G. Stein, Angew. Chem, 1937, 50, 514: DOI:10.1002/ange.19370502804
- ↑ D. Skála, J. Hanika, Pet. Coal, 2003, 45, 105: PDF
- ↑ A. G. Schultz and L. Flood, J. Org. Chem., 1986, 51, 838-841. DOI:10.1021/jo00356a016
- ↑ A. G. Shultz, L. Flood and J. P. Springer, J. Org. Chemistry, 1986, 51, 838.DOI:10.1021/jo00356a016
- ↑ Leleu, Stephane; Papamicael, Cyril; Marsais, Francis; Dupas, Georges; Levacher, Vincent. Tetrahedron: Asymmetry, 2004, 15, 3919-3928.DOI:10.1016/j.tetasy.2004.11.004
- ↑ S. W. Elmore and L. A. Paquette, Tet. Letters, 32, 3. pp 319-322, 1991, DOI:10.1016/S0040-4039(00)92617-0 10.1016/S0040-4039(00)92617-010.1021/ja00274a016 /10.1016/S0040-4039(00)92617-0 10.1016/S0040-4039(00)92617-0 10.1016/S0040-4039(00)92617-010.1021/ja00274a016
- ↑ A. B. McEwent and P.V.R. Schleyer, J. Am. Chem. SOC., 1986, 108, 3951-3960. DOI:10.1021/ja00274a016
- ↑ H. Kusama, R. Hara, S. Kawahara, T. Nishimori, H. Kashima, N. Nakamura, K. Morihira and I. Kuwajima, J. Am. Chem. Soc., 2000, 122, 3811-3820. DOI:10.1021/ja9939439
- ↑ 11.0 11.1 B. Halton, S.G.G. Russell, J. Org. Chem., 1991, 56, 5553: DOI:10.1021/jo00019a015
- ↑ 12.0 12.1 B. Halton, R. Boese and H. S. Rzepa., J. Chem. Soc., Perkin Trans 2, 1992, 447. DOI:10.1039/P29920000447
- ↑ 13.0 13.1 G. Socrates, Infrared and Raman Characteristic Group Frequencies, Third Edition, 2001, Pg. 65
- ↑ 14.0 14.1 14.2 14.3 K.A. Ahrendt, C.J. Borths, D.W.C. Macmillan, J. Am. Chem. Soc., 2000, 122, 4243: DOI:10.1021/jo00019a015
- ↑ J. Clayden. N. Greeves, S. Warren and P. Wothers, Organic Chemistry, 2000, First Edition, Pg. 913