Rep:Mod:leoboon
Module 1
All optimisations are done with the MM2 method unless noted otherwise.
Dimerisation of cyclopentadiene and hydrogenation
Cyclopentadiene dimerises readily at room temperature to produce one of either 1 or 2, depeneding whether the substituents of the transition state are exo (1) or endo (2). The endo product is almost exclusively produced. [1]
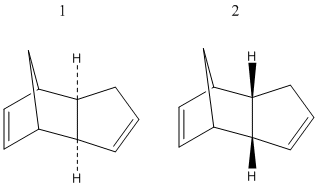
In order to determine whether the Diels-Alder mechanism that leads to this product is kinetically or thermodynamically controlled, the structures of 1, 2 and the respective transition states leading to them were built using ChemBio3D, and their energies minimised using MM2.
| Molecule | Energy /hartree |
|---|---|
| Transition state leading to 1 | 0.4275 |
| Transition state leading to 2 | 0.4273 |
| Dimer 1 | 0.050 |
| Dimer 2 | 0.054 |
 |
 |
 |
 |
After analysis, it is clear that the dimerisation mechanism is most likely kinetically controlled. While the energy of 1 is lower than the energy of 2, the energy of the transition state leading to 2 is lower than the one leading to 1.
In a similar fashion, the hydrogenation of the endo product was investigated. Only one of two alkene bonds is initially hydrogenated, yielding either 3 or 4. In order to assess which, the two molecules and the transition states leading to them were built and analysed.
| Molecule | Energy /hartree |
|---|---|
| Transition state leading to 3 | 0.693 |
| Transition state leading to 4 | 0.715 |
| Dimer 3 | 0.057 |
| Dimer 4 | 0.049 |
 |
 |
 |
 |
4 seems to be the preferred product of hydrogenation, if we assume the pathway to be thermodynamically controlled.
| Mode | Contribution in 3 /hartree | Contribution in 4 /hartree |
|---|---|---|
| Stretch | 1.24 | 1.09 |
| Bend | 18.99 | 14.50 |
| Stretch-Bend | -0.76 | -0.54 |
| Torsion | 12.03 | 12.51 |
| Non-1,4 VDW | -1.46 | -1.05 |
| 1,4 VDW | 5.72 | 4.50 |
| Dipole/Dipole | 0.16 | 0.14 |
The crucial difference between the two molecules, as gathered from the breakdown of the energy contributions, is the bend contribution. We must asusme therefore 3 to be more rigid and hence more energetic.
Stereochemistry of Nucleophilic additions to a pyridinium ring (NAD+ analogue)
The nucleophilic addition to a pyridinium ring was investigated. The reactions in question involve the methylation using a Grignard reagent of compound 5 and the addition of aniline to compound 7. In both cases the result is surprising at first glance, as the additions appear to add rather bulky groups onto the same face of the carbonyl oxygen, and one might expect the steric clash to favour the addition on the opposite side. Molecular modelling allows us to visualize the preferred geometry of the molecules 5 and 7, based upon the model with the lowest energy after the MM2 optimisation. In the same way, 6 and 8 were also analysed, as well as the alternate enantiomers where the addition occurs from the opposite face. In both cases, the enantiomer has lower energy. Therefore, there must be other factors that influence the additions.

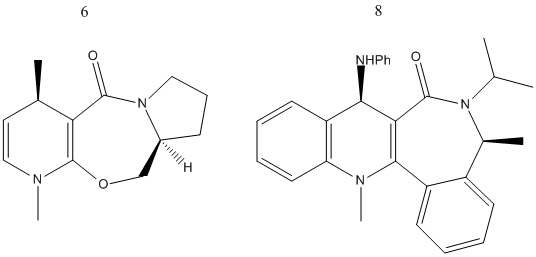
| Molecule | Energy /hartree |
|---|---|
| Molecule 5 | 0.069 |
| Molecule 6 | 0.0597 |
| Enantiomer of 6 | 0.0596 |
| Molecule 7 | 0.101 |
| Molecule 8 | 0.1025 |
| Enantiomer of 8 | 0.1018 |
The first reaction, the methylation with a Grignard reagent, involves the addition of a quite bulky MeMgI from the top face, where it supposedly clashes with the carbonyl oxygen. However, this unfavourable interaction is overshadowed by the chelating effect of the oxygen with the magnesium, that favours the addition on that side. Although that leads to the enantiomer with the highest energy, the pathway is therefore more favourable, and we can consider this as a kinetically controlled reaction.[2]
The second reaction, while at a first look appears to add a bulky aniline on the same side of the oxygen, actually adds it on the opposite side. A correct model of molecule 7 will reveal that the oxygen is slightly bent downwards, away from the plane of the quinoline fragment and hence the addition from the top is actually sterically favoured over the addition from the bottom.[3]
 |
 |
 |
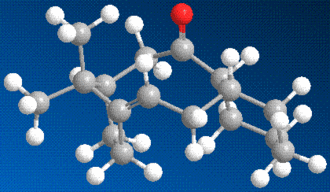
Stereochemistry and Reactivity of an Intermediate in the Synthesis of Taxol
The molecule shown presents atropisomerism, where the two isomers are only different in the rotation of one of the bonds, which is locked due to the overall structure. In this molecule, an intermediate in the synthesis of taxol, the bond in question is the carbonyl group, which can either point up (9) or down (10).

Using the MM2 method, the two isomers were investigated and their energies were approximated. Due to the good degree of flexibility of the rings involved, it took some tinkering in order to reach the minimum energy forms.
| Molecule | Energy /hartree |
|---|---|
| Isomer 9 | 0.078 |
| Isomer 10 (initial) | 0.085 |
| Isomer 10 (best) | 0.071 |
Initially it was believed that 9 was the most stable isomer, but after a consultation with literature that claimed 10 to be instead the more stable one, [4], the structures were modified in order to account for this. In particular the structure of the terminal, non-bridging cyclohexane was modified. This gave a structure that has an energy in good accordance with the literature value.
 |
 |
 |
 |
 |
Being an intermediate in the synthesis of taxol, 10 then undergoes several functionalisation reactions to reach the final product. The alkene however is very unreactive. The reasons for this was found to be its location near a bridgehead[5] which is particularly stable (hyperstable) due to similarity to a trans-cycloalkene unit[6]
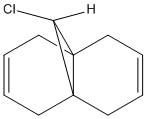
Regioselective Addition of Dichlorocarbene
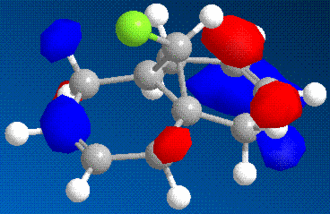
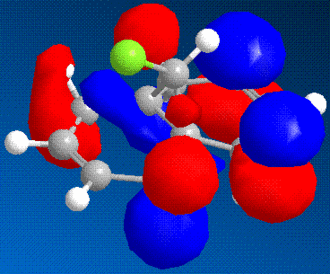
It is possible to use molecular modelling to predict the reactivity of molecules. In the previous examples, the basis for the reasonings were mainly based on energy and strain, by comparing the internal energy of the molecules and using this to rationalise the products of certain reactions. However, sometimes the answer lies within the molecular orbitals of the molecule, and hence the calculation must become more sofisticated. The molecule in question is 9-chloromethanonaphthalene. Using the MM2 method to obtain a first rough minimisation of the energy, the MOPAC calculation (PM6 and RM1 methods) was used to gain a reasonable approximation of the surfaces of the molecular orbitals. These should give us enough tools to determine at which alkene should an electrophilic addition of dichlorocarbene, CCl2, whether on the side with the chlorine or the opposite.
 |
 |
 |
 |
 |
 |
 |
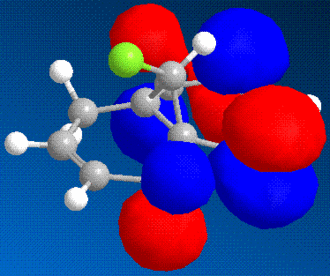 |
As it can bee seen from the diagrams, the HOMO seems to clearly reside on the alkene bond opposite the chlorine (here in green).
Further proof of the location of the reactive site comes from IR calculations. We have determined the alkene bond opposite the chlorine to be the location of the HOMO, and hence we expect this bond to be weaker. If it is weaker, it will stretch at a lower frequency than the alkene bond on the other ring. Using the PM6 optimised geometry, the Vibrational IR spectrum of 9-chloromethanonaphthalene and its monoalkene related form where the alkene opposite the chlorine has been hydrogenated was calculated by Gaussian. This gave the expected results as the alkene close to the chlorine stretches consistently in the 1753-1757 cm-1 region, while the other alkene stretches lower at 1737 cm-1, confirming that that bond is indeed weaker, and electrophilic addition should happen at that site. Experimental results confirm this.[7] The chlorine-carbon bond stretching frequency is in the 528-540 cm-1 region.
Project
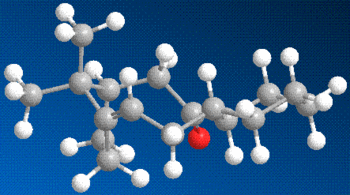
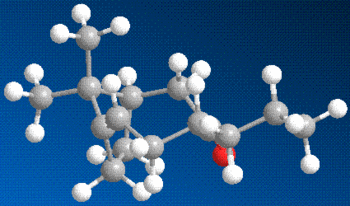
Molecular modelling is a powerful tool that allows us to calculate and predict several properties of molecules. Using a combination of methods, we are able to rationalise certain reactions and approximate reality with a good degree of closeness. For example, the ketone 1 is reduced using the Birch Reduction method to one of the alcohols 2 or 3. This reaction is highly stereoselective to give alcohol 2 as the main product.[8]

In order to rationalise this observation, the models of the three molecules were built, minimised using MM2 and further optimised using Gaussian. The NMR and the optical rotations (where applicable) were calculated. Underneath you can see the three molecules in question, reactant, preferred product and unpreferred product, in that order.
Reactant |
Preferred product |
Unpreferred product |
The
13C NMR was predicted using the DFT=MPW1PW91 method and the 6-31G(d,p) basis set. This was compared with the literature values reported in[9].
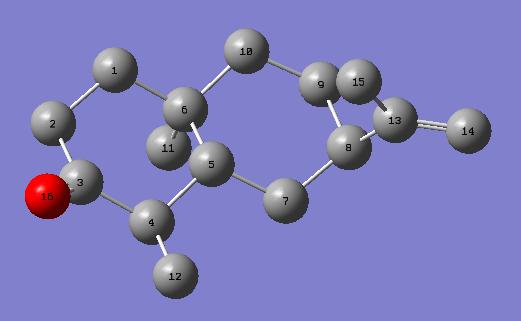

| Carbon Atom in reference | Shift of reference /ppm | Carbon atom in calculation | Shift of calculation /ppm |
|---|---|---|---|
| 3 | 213.25 | 3 | 207.95 |
| 11 | 146.28 | 13 | 150. 4 |
| 13 | 111.06 | 14 | 110.17 |
| 5 | 45.66 | 5 | 47.53 |
| 4 | 45.24 | 4 | 47.04 |
| 1 | 41.74 | 1 | 42.34 |
| 7 | 38.32 | 8 | 41.17 |
| 2 | 38.20 | 10 | 39.89 |
| 9 | 36.32 | 2 | 38.82 |
| 10 | 33.99 | 6 | 34.05 |
| 6 | 27.54 | 7 | 30.41 |
| 8 | 23.02 | 9 | 27.58 |
| 12 | 22.71 | 15 | 24.23 |
| 15 | 16.10 | 11 | 16.5 |
| 14 | 11.18 | 12 | 13.67 |
| Carbon Atom in reference | Shift of reference /ppm | Carbon atom in calculation | Shift of calculation /ppm |
|---|---|---|---|
| 11 | 147.11 | 13 | 151.1 |
| 13 | 110.67 | 14 | 109.96 |
| 3 | 76.86 | 3 | 74.7 |
| 5 | 43.22 | 5 | 45 |
| 1 | 39.93 | 4 | 41,31 |
| 7 | 39.19 | 8 | 41,31 |
| 4 | 38.88 | 1 | 40.16 |
| 9 | 37.10 | 10 | 39.74 |
| 10 | 33.78 | 6 | 34.21 |
| 2 | 30.92 | 7 | 32.52 |
| 6 | 26.05 | 2 | 30.03 |
| 8 | 23.08 | 9 | 24.62 |
| 12 | 22.82 | 15 | 24.35 |
| 15 | 16.68 | 11 | 17.2 |
| 14 | 14.87 | 12 | 15.32 |
As you can see, there is a general degree of accordance between the calculated 13C NMR and the experimental one. The best matches appear at both ends of the table, and the values in the middle are a bit worse in terms of similarity. This is all under the assumption that while the carbons were labeled in different ways by Gaussian and the literature, they still identify the same carbon. The NMR is fairly typical, with the same range of values one would expect from a cyclic compound with an oxygen.
The optical rotation analysis will be added once the job on SCAN finishes. The prediction is that the two products will have identical but opposite in sign rotation that will be the best instrument to distinguish between them.
In the end, the preferred product is favoured over the other probably due to steric reasons. In it, the alcohol is in an equatorial position while in the unpreferred form it is in axial, where it will experience 1-3 diaxial strain.
References
- ↑ Alder, K.; Stein, G. Liebigs Ann. Chem. 1933, 504, 210−257
- ↑ A. G. Shultz, L. Flood and J. P. Springer, J. Org. Chemistry, 1986, 51, 838
- ↑ Leleu, S.; Papamicael, C.; Marsais, F.; Dupas, G.; Levacher, V. Tetrahedron: Asymmetry, 2004, 15, 3919-3928
- ↑ Paquette, L. A.; Combrink, K. D.; Elmore, S. W.; Rogers, R. D. J. Am. Chem. Soc. 1991, 113, 1335−1344
- ↑ W.F. Maier and P.v.R. Schleyer. J. Am. Chem. Soc. 1981 103, 1891–1900
- ↑ A.B. McEwen and P.v.R. Schleyer. J. Am. Chem. Soc. 1986 103 3951–3960
- ↑ Halton, B.; Russell, S. G. G.; J. Org. Chem., 1991, 56, 5553
- ↑ Castellanos, L; Duque, C.; Rodriguez, J; Jimenez, C. Tetrahedron, 1991, 63, 12
- ↑ Castellanos, L; Duque, C.; Rodriguez, J; Jimenez, C. Tetrahedron, 1991, 63, 12