Rep:Mod:leh2313
Introduction
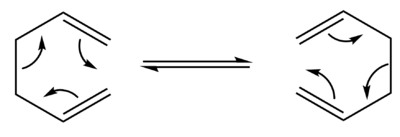
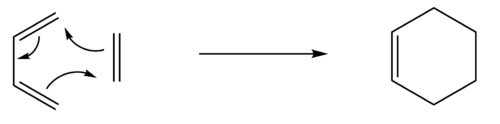
The transition state is a particular point along a reaction coordinate for a chemical reaction, where the configuration coincides with the highest potential energy. If the reaction is said to be perfectly irreversible, the reactant will always go on to form the product.[1] Owing to the quantum nature of the transition state, it cannot be studied directly; its lifetime is essentially zero.[2] Spectroscopic techniques, such as Femtochemical IR, have been developed to probe as close to the transition state as is possible within the restrictions of the timescale. Hammond's postulate provides an alternative method of studying the transition state. This hypothesis states that the transition state will resemble either the reactants or products, determined by whichever is higher in energy.[3] These methods are limited in their ability to provide physical data, however, which has led to the wide use of computational methods.
The [3,3]-sigmatropic shift rearrangement of 1,5-hexadiene has been subject to many computational studies endeavouring to discover its mechanism. The now generally accepted conclusion is that the rearrangement takes place via the "chair" or higher energy "boat" transition states.[4] We will use employ such computational methods using the example of 1,5-hexadiene to show how they can give statistical data that is in agreement with experimental studies. Using the GaussView software, we will construct and optimise the reactants and products at the HF/3-21G and more advanced B3LYP/6-31G* level. This will give us information about the point group, vibrational frequencies and the potential energy, allowing us to compare these to experimental data.
Using three methods, we will characterise the transition states and locate the low-energy minima on the potential energy surface of the Cope rearrangement. For the most basic of these methods, will we use the aforementioned Hammond's postulate to optimise the assumed transition state at the HF/3-21G level. We will then use the frozen coordinate method, also at the HF/3-21G level before, finally, using the QTS2 technique. The QTS2 method allows us to state the reactant and product and interpolate between the two to determine the transition state. We will then show it is possible to characterise the transition states of Diels-Alder reactions by utilising the same methods as for the Cope rearrangement.
Nf710 (talk) 09:47, 16 December 2015 (UTC) Excellent understanding of the experimental techniques used when studying this reaction in the lab however you could have gone into more detail when talking about the computational methods.
Cope Rearrangement
The Cope rearrangement is a pericyclic and concerted [3,3]-sigmatropic rearrangement of 1,5-dienes, first developed by Arthur C. Cope. This rearrangement can proceed via the "chair" or "boat" transition states.
The example we will be using is the thermal isomerisation of 1,5-hexadiene.
Optimising the reactants and products
A first molecule of 1,5-hexadiene was drawn with an "anti1" linkage and optimised at the HF/3-21G level. A summary is provided below and the .log file can be found here.
| anti1 | |||||
|---|---|---|---|---|---|
| File Name | anti_opt | ||||
| File Type | .chk | ||||
| Calculation Type | FOPT | ||||
| Calculation Method | RHF | ||||
| Basis Set | 3-21G | ||||
| Charge | 0 | ||||
| Spin | Singlet | ||||
| Total Energy | -231.69260235 | a.u. | |||
| RMS Gradient Norm | 0.00001824 | a.u. | |||
| Imaginary Freq | |||||
| Dipole Moment | 0.2021 | Debye | |||
| Point Group | C2 |
The level of optimisation gives a C=C bond length of 1.316 Å and a central C-C bond length of 1.552 Å. The simplicity of this basis set optimisation is highlighted by the discrepancy to a literature value of 1.535 Å for the central C-C bond. The torsional angle TC1-C2-C3-C4, however, is calculated to be 115.2°, which compares favourably to literature value of 116.0° while the TC2-C3-C4-C5 angle is 176.9°, compared to the 176.8° literature value.[5]
The "gauche4" linkage of 1,5-hexadiene was the next to be constructed and optimised, again at the HF/3-21G level. The .log file can be found here.
| gauche4 | |||||
|---|---|---|---|---|---|
| File Name | gauche_opt | ||||
| File Type | .chk | ||||
| Calculation Type | FOPT | ||||
| Calculation Method | RHF | ||||
| Basis Set | 3-21G | ||||
| Charge | 0 | ||||
| Spin | Singlet | ||||
| Total Energy | -231.69153032 | a.u. | |||
| RMS Gradient Norm | 0.00001866 | a.u. | |||
| Imaginary Freq | |||||
| Dipole Moment | 0.1281 | Debye | |||
| Point Group | C2 |
At -231.69153 hartrees, the "gauche4" is, as expected, higher in energy that the "anti1" configuration. Due to rotation around the sp3 hybridised carbon-carbon sigma bond, the two ethene substituents find themselves in closer proximity to each other. There is a steric hindrance between the two substituents and as a result, the potential energy is lifted relative to the "anti1" configuration. The optimisation of "gauche4" at this level yields a C=C bond length of 1.316 Å and a central C-C bond length of 1.555 Å. Again, as with "anti1", there is disparity with the literature value of 1.539 due to the simple optimisation. Meanwhile TC1-C2-C3-C4 is 109.4° and TC2-C3-C4-C5 is 63.7°, confirming its gauche nature. The literature provides values of 111.5° and 60.6° respectively.[5]
In accordance with the above explanation, it is to be expected that "anti1" would be lowest in energy but the "gauche3" linkage was optimised and found to be marginally lower in energy. The .log can be found here.
| gauche3 | |||||
|---|---|---|---|---|---|
| File Name | gauche3_opt_lh2313 | ||||
| File Type | .chk | ||||
| Calculation Type | FOPT | ||||
| Calculation Method | RHF | ||||
| Basis Set | 3-21G | ||||
| Charge | 0 | ||||
| Spin | Singlet | ||||
| Total Energy | -231.69266120 | a.u. | |||
| RMS Gradient Norm | 0.00001176 | a.u. | |||
| Imaginary Freq | |||||
| Dipole Moment | 0.3406 | Debye | |||
| Point Group | C1 |
This surprisingly low energy for "gauche3" may be due to an attractive interaction between the vinyl proton and π orbital.[6] After optimisation, the central C-C bond length is 1.553 Å, compared to a length of 1.538 Å provided by the literature. The torsion angle of 120.9° for TC1-C2-C3-C4 and 67.7° for TC2-C3-C4-C5 support its gauche form but do not lie as close to literature data as the previous examples, at 117.9° and 64.8°.[5]
Comparison of HF/3-21G and B3LYP/6-31G* theory levels
Nf710 (talk) 09:51, 16 December 2015 (UTC) Well done in the below section for finding all the literature values.
We then used the example of the "anti2" linkage to compare the physical data obtained at the HF/3-21G and B3LYP/6-31G* levels of theory. The HF/3-21G level was the first used to optimise the "anti2" conformation. The .log file can be found here.
| anti2 | |||||
|---|---|---|---|---|---|
| File Name | anti2_opt_lh2313 | ||||
| File Type | .chk | ||||
| Calculation Type | FOPT | ||||
| Calculation Method | RHF | ||||
| Basis Set | 3-21G | ||||
| Charge | 0 | ||||
| Spin | Singlet | ||||
| Total Energy | -231.69253528 | a.u. | |||
| RMS Gradient Norm | 0.00001339 | a.u. | |||
| Imaginary Freq | |||||
| Dipole Moment | 0.0003 | Debye | |||
| Point Group | Ci |
The "anti2" configuration was then run at the B3LYP/6-31G* theory level. The .log file can be found here.
| anti2 | |||||
|---|---|---|---|---|---|
| File Name | anti2_opt631_lh2313 | ||||
| File Type | .chk | ||||
| Calculation Type | FOPT | ||||
| Calculation Method | RHF | ||||
| Basis Set | 6-31G(D) | ||||
| Charge | 0 | ||||
| Spin | Singlet | ||||
| Total Energy | -231.61171166 | a.u. | |||
| RMS Gradient Norm | 0.00001227 | a.u. | |||
| Imaginary Freq | |||||
| Dipole Moment | 0.0000 | Debye | |||
| Point Group | Ci |
A comparison of the physical data obtained from the different levels of theory is shown below:
| HF/3-21G | B3LYP/6-31G* | ||
|---|---|---|---|
| Geometry/ ° | TC1-C2-C3-C4 | 114.7 | 118.6 |
| TC2-C3-C4-C5 | 180.0 | 180.0 | |
| TC3-C4-C5-C6 | -114.7 | -118.6 | |
| Bond Length/ Å | C1-C2 | 1.316 | 1.334 |
| C2-C3 | 1.509 | 1.504 | |
| C3-C4 | 1.553 | 1.548 | |
On changing the theory level from the HF/3-21G to B3LYP/6-31G*, the C=C bond length increases from 1.316 Å to 1.334 Å.[7] This is in very good agreement with the literature value of 1.340 Å. The other bond lengths change minimally. This shows the benefit of the higher level of theory, despite the increased amount of time taken. The torsion angle also increases when optimised under the the B3LYP/6-31G* level.
Nf710 (talk) 10:06, 16 December 2015 (UTC) good geom comparison and also your energies here are correct.
Frequency analysis
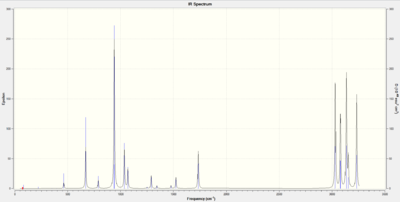
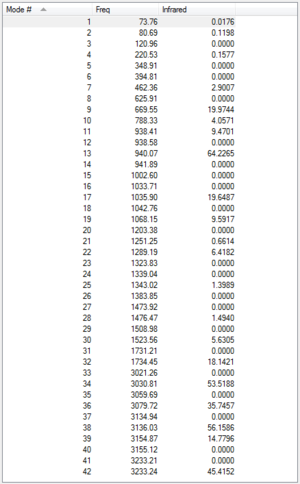
Following the optimisation at the B3LYP/6-31G*, a frequency analysis was performed at the same theory level. This gave us a list of vibrational frequency modes, of which there were no imaginary, and an infra-red spectrum as shown. In the .log file (which can be found here) the below list of thermal energies can be found:
| Value/ Hartree per particle | |
|---|---|
| Sum of electronic and zero-point Energies | -234.469215 |
| Sum of electronic and thermal Energies | -234.461866 |
| Sum of electronic and thermal Enthalpies | -234.460922 |
| Sum of electronic and thermal Free Energies | -234.500800 |
The first of these values corresponds to the potential energy at 0 K, with the zero-point vibrational energy included, while the second gives the same energy but at 298 K and 1 atm. There are contributions from the vibrational, translational and rotational modes. The third includes a correction for RT and the final energy adds the entropic contribution.
Optimising the "chair" and "boat" transition structures
In this section we optimise the transition state of the Cope rearrangement using three different methods. For the first two of these methods, where we compute the force constants at the start of the calculation then use the frozen coordinate method, we use a presumed transition state. Therefore, before we could do this, we optimised an allyl fragment at the HF/3-21G level of theory. This fragment is shown below and the .log file is available here.
As an optimisation calculation needs to know where the negative direction of curvature lies, transition state optimisations are not as simple as minimisations. With a reasonably accurate depiction of the transition state, this information can be acquired by computing the force constant matrix in the first step of optimisation. This was done by constructing a rough "chair" transition state formed from two allyl fragments such that the terminal ends were 2.2 Å apart. This structure was optimised and one imaginary frequency was produced at -817.88 cm-1 corresponding to the Cope rearrangement. This is animated in Figure 5, while the optimised transition state is shown below and the .log file of the optimisation is available here.
Nf710 (talk) 10:10, 16 December 2015 (UTC) Good understanding of how the frequency analysis works
A better proposition for the transition structure can be created by freezing the reaction coordinates and minimising the rest of the molecule. The result of this is shown and the .log file is available here.
The reaction coordinate is then unfrozen once the molecule is completely relaxed then a transition state optimisation can be undertaken. This was the next method to be performed and the .log file provided here.
Using the first technique, a distance of 2.02 Å was produced between the terminal ends of the allyl fragments after optimisation, while in the frozen coordinate method they are set to exactly 2.2 Å.
The final method is the QTS2 technique. Using this method, we optimised the "boat" transition structure. The process by which this method optimises the transition structure is to provide the reactants and products and the calculation will interpolate between the two of them to find the transition structure. The "anti2" structure provided our starting point for our reactant and product. The central torsional angle was altered to 0° and the two central bond angles were set to 100°. The QTS2 calculation was run, producing the "boat" transition structure shown below. An animation of the Cope rearrangement is provided in Figure 6 and the .log file is available here.
Nf710 (talk) 10:14, 16 December 2015 (UTC) in future put the vibrations in the script, i will let you off as you have have linked the log file.
A technique called the Intrinsic Reaction Coordinate (IRC) method allows us to transcend the minimum energy path from the transition structure down to its local minimum on a potential energy surface. It does this by taking a series of steps in the direction where gradient is steepest. This allows us to discover the conformer that the transition structure connects. Using the first "chair" transition state we optmised, it produces the below structure after 50 steps with the .log file available here.
Nf710 (talk) 10:15, 16 December 2015 (UTC) You should have put the graph in.
This structure was then minimised to give us the conformer of 1,5-hexadiene. The produced conformer was the "anti4" configuration due to its C1 point group, shown in the .log file here.
The IRC can be run to its completion, negating the need to minimise the structure given after 50 steps but this can take a very long time and does not always give the correct structure. Alternatively, the IRC can be run while computing force constants at every step. This gives the most reliable result but again this is time consuming and hardware intensive.
By reoptimising the "chair" and "boat" transition structures at the B3LYP/6-31* theory level we can get an accurate prediction of the potential energy. We can then compare these to the optimised reactants, in order to work out an estimate for the activation energy. The "chair" structure was reoptimised first and the .log file is available here. The "boat" transition structure was optimised next and the .log for that is available here.
We have already optimised the "anti2" conformer at the B3LYP/6-31G* level so we can use that as a reference in comparison to the transition structures. The potential energy of this reactant minus that of the transition structures will give us the activation energy for that particular transition structure. The potential energies are summarised below:
| HF/3-21G | B3LYP/6-31G* | |||||
|---|---|---|---|---|---|---|
| Electronic energy | Sum of electronic and zero-point energies at 0 K | Sum of electronic and thermal energies at 298.15 K | Electronic energy | Sum of electronic and zero-point energies at 0 K | Sum of electronic and thermal energies at 298.15 K | |
| "Chair" TS | -231.619322 | -231.466701 | -231.461341 | -234.556984 | -234.414932 | -234.409011 |
| "Boat" TS | -231.602802 | -231.450928 | -231.445299 | -234.543079 | -234.402363 | -234.396017 |
| Reactant ("anti2") | -231.692535 | -231.539539 | -231.532566 | -234.611710 | -234.469215 | -234.461866 |
1 hartree is equal to 627.509 kcal/mol, so activation energies are shown below in kcal/mol:
| HF/3-21G | B3LYP/6-31G* | Experimental[4] | |||
|---|---|---|---|---|---|
| 0 K | 298.15 K | 0 K | 298.15 K | 0 K | |
| ΔE ("Chair") | 45.71 | 44.69 | 34.06 | 33.17 | 33.5 ± 0.5 |
| ΔE ("Boat") | 55.60 | 54.76 | 41.95 | 41.32 | 44.7 ± 2.0 |
The higher theory level produces results that lie much closer to the literature. Therefore, we can conclude from these results that, as expected, the "boat" transition state provides a higher energy pathway for the Cope rearrangement. It also shows us that the activation energy is smaller for the rearrangement at a higher temperature. This is because the initial energy of the reactant is closer to the transition state energy at higher temperatures.
Nf710 (talk) 10:21, 16 December 2015 (UTC) your energies are correct. however you didn't deduce that geometries are well approximated for lower basis sets. This is a well formatted wiki, however you should have included some of the data in the report and also gone into more detail on the theory.
The Diels-Alder Cycloaddition
The Diels-Alder reaction is a organic pericyclic reaction between a substituted alkene and a conjugated diene. Specifically knows as a [4+2]-cycloaddition, the π orbitals on the alkene, or the dieneophile, are used to form σ bonds with the diene to form a substituted cyclohexene.
Whether a reaction is allowed or forbidden depends on how many π electrons are involved. A reaction is allowed if the HOMO of one reactant can interact with the LUMO of the other. If the interacting HOMO-LUMO have different symmetry properties, then a significant overlap density is not possible and the reaction is forbidden. A π orbitals on the substituent of the dienophile can stabilise the regiochemistry by interacting with the new double bond that is formed in the product. As before, we will study the nature of the transition state for the basic Diels-Alder reaction, a case where both reactants have substituents and where secondary orbital effects are possible.
Optimisation of the transition state
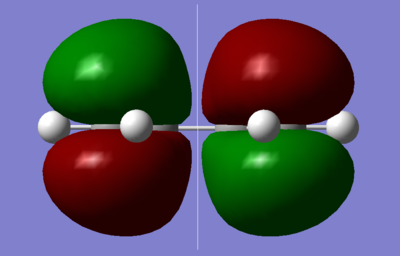
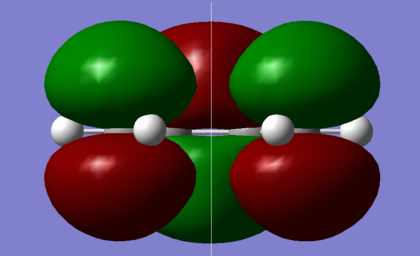
The π-π* orbitals of ethene and the HOMO-LUMO of butadiene are the major orbital interactions in a Diels-Alder reaction. The cis configuration of butadiene was optimised under the semi-empirical AM1 level, in order to visualise the molecular orbitals. The .log file is available here.
| HOMO | LUMO |
|---|---|
|
|
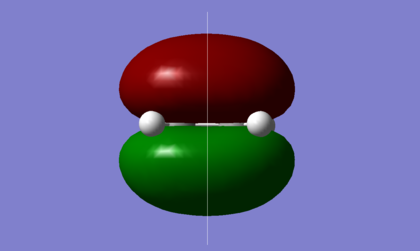
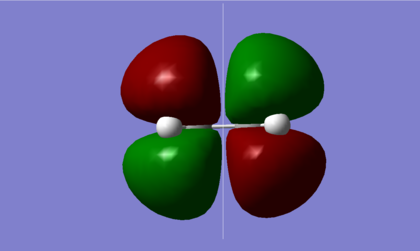
As shown in the diagrams above, the LUMO of butadiene is symmetric, s, with respect to the plane shown, while the HOMO of butadiene is asymmetric, a. An ethene molecule was then optimised, as shown below with the .log file available here.
| HOMO | LUMO |
|---|---|
|
|
In ethene, however, it is the HOMO that is symmetric, s, and the LUMO is asymmetric, therefore it is the opposing HOMO-LUMO pairs that interact.
(This is true, but which MO pairs form the HOMO and LUMO of the TS? Tam10 (talk) 12:05, 10 December 2015 (UTC))
The transition structure for the most basic Diels-Alder reaction can then be optimised by placing the ethene molecule 2.1 Å away from the optimised cis butadiene molecule. The .log file is available here and upon optimisation, the below structure is produced:
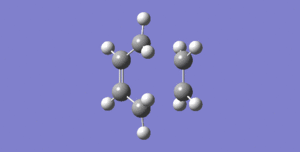

This shows that an envelope conformation maximises the overlap between the ethene π orbitals and the π orbitals of cis butadiene. The partially formed C-C σ bond has bond length of 2.2 Å, much longer than a typical C-C bond, which is to be expected for a transition structure. A frequency was run simultaneously, allowing for the visualisation of the synchronous reaction path, as is shown in Figure 7, and the lowest postitive vibrational mode in Figure 8.
(What are the values for these vibrations? You should also state the typical C-C lengths with a reference Tam10 (talk) 12:05, 10 December 2015 (UTC))
| HOMO | LUMO |
|---|---|
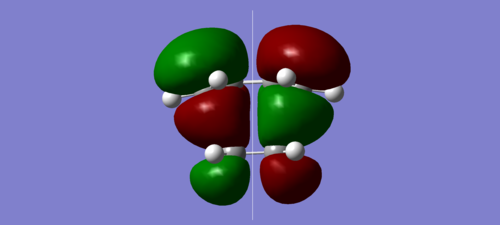
|
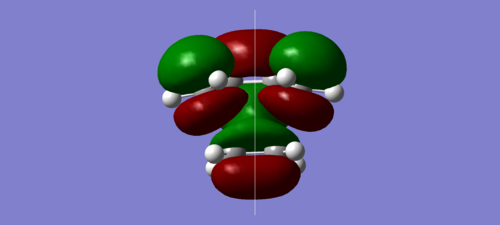
|
It can be seen above that the HOMO of the transition structure is asymmetric, while the LUMO is symmetric.
The regioselectivity of the Diels-Alder reaction can be studied by using the example of cyclohexa-1,3-diene and maleic anhyride.
This reaction is kinetically controlled, which means the exo form is the higher in energy. We can show this by optimising the endo and exo forms of the transition state. Before we could do this, we had to optimise cyclohexa-1,3-diene and maleic anhydride at the semi-empirical AM1 level. The .log files for that can be found here and here respectively. We could then optimise the endo form which is shown below with the .log file available here.
| endo | |||||
|---|---|---|---|---|---|
| File Name | maleic_ts_endo_lh2313 | ||||
| File Type | .chk | ||||
| Calculation Type | FREQ | ||||
| Calculation Method | RAM1 | ||||
| Basis Set | ZDO | ||||
| Charge | 0 | ||||
| Spin | Singlet | ||||
| Total Energy | -0.05150471 | a.u. | |||
| RMS Gradient Norm | 0.00001588 | a.u. | |||
| Imaginary Freq | |||||
| Dipole Moment | 6.1665 | Debye | |||
| Point Group | C1 |
The exo form was then constructed and optimised as shown below. The summary table is shown and the .log file is available here.
| exo | |||||
|---|---|---|---|---|---|
| File Name | maleic_exo_ts_lh2313 | ||||
| File Type | .chk | ||||
| Calculation Type | FREQ | ||||
| Calculation Method | RAM1 | ||||
| Basis Set | ZDO | ||||
| Charge | 0 | ||||
| Spin | Singlet | ||||
| Total Energy | -0.05041983 | a.u. | |||
| RMS Gradient Norm | 0.00001144 | a.u. | |||
| Imaginary Freq | |||||
| Dipole Moment | 6.1665 | Debye | |||
| Point Group | C1 |
This optimisation demonstrates the expected result, that the exo conformation is higher in energy by 0.00108 hartrees. The endo product is the more thermodynamically stable because there is less steric hindrance between the 5- and 6-membered rings. This means, as the reaction is reversible, it will eventually form the major product. The exo form is the kinetic product, however, so is formed much quicker than the endo form. This is due to a secondary orbital overlap effect between the carbonyl groups of the dienophile and the developing π bond.[8]
(Differences in energy can be converted into kj/mol or kcal/mol Tam10 (talk) 12:05, 10 December 2015 (UTC)) (You said the exo TS is higher in energy, so wouldn't that make it less kinetically favourable? In addition, secondary orbital overlap would only occur in the endo TS. I'm assuming this is a typo? Tam10 (talk) 12:05, 10 December 2015 (UTC))
| exo | endo |
|---|---|
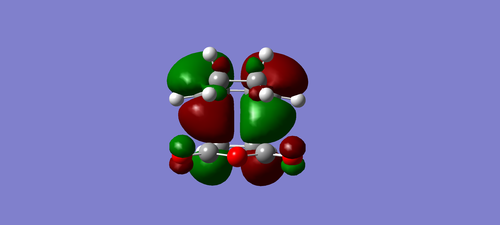
|
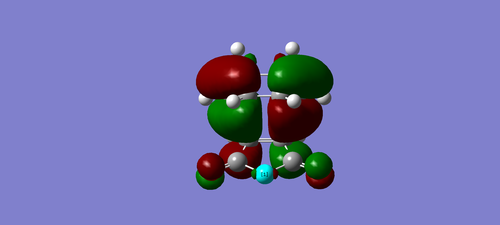
|
Conclusion
This study has shown the power of computational chemistry in a variety of ways, such as enabling us to show how different conformations have compared in potential energies and tallied with experimental data even at low theory levels. We have obtained data such as point groups and performed frequency analyses to display vibrational modes. We have been able to predict transition states and the reactants that formed it, using the information to calculate activation energies that lie very close to experimental values. These are sophisticated calculations that can help us to visualise molecular orbitals and take into account secondary orbital effects.
References
- ↑ Solomons, T.W. Graham & Fryhle, Craig B. Organic Chemistry (8th ed.). 2004. John Wiley & Sons, Inc. ISBN 0-471-41799-8.
- ↑ Lewars, G. E. Computational Chemistry: Introduction to the Theory and Applications of Molecular and Quantum Mechanics (2nd ed.). 16. 2011. Springer. ISBN 978-9048138609.
- ↑ Hammond, G. S. "A Correlation of Reaction Rates". J. Am. Chem. Soc. 1955. 77: 334–338. DOI:10.1021/ja01607a027
- ↑ 4.0 4.1 Wiest, O., Black, A. K., Houk, K. N. "Density Functional Theory Isotope Effects and Activation Energies for the Cope and Claisen Rearrangements". J. Am. Chem. Soc. 1994. 116 (22), pp 10336–10337. DOI:10.1021/ja00101a078 Cite error: Invalid
<ref>tag; name "ja00101a078" defined multiple times with different content - ↑ 5.0 5.1 5.2 Rocque, G. B., Gonzales, J. M and Schaefer III, H. F. "An analysis of the conformers of 1,5-hexadiene". Molecular Physics. 2002. 100: 441–446. DOI:10.1080/00268970110081412
- ↑ Nishio, M., Hirota, M. "CH/π interaction: Implications in organic chemistry". Tetahedron. 1989. 45: 7201–7245. DOI:10.1016/S0040-4020(01)89185-7
- ↑ Graner, G., Hirota, E., Iijima, T., Kuchitsu, K., Ramsay, D. A., Vogt, N., Vogt, J. Molecules containing five or more carbon atoms. 2003. 257 DOI:10.1007/b75952
- ↑ Clayden, J., Greeves, N., Warren, S., Wothers, P. Organic Chemistry (2nd ed.). 2012. OUP Oxford. ISBN 978-0199270293.