Rep:Mod:lateralus
Year 3 Computational Lab: Transition States
Harry Wilkinson
Introduction
This computational experiment examines the transition states of two pericyclic reactions. Firstly, the Cope Rearrangement of 1,5-hexadiene and then, a Diels-Alder Cycloaddition reaction. Transition states are the point of a reaction at which energy is the highest, therefore they have zero lifetime and cannot be studied directly by spectroscopy or any other method. Therefore they must be either predicted qualitatively, by use of the Hammond postulate, or calculated, as is done in this experiment. The program that we are using, GaussView can calculate transition states in a few different ways. The simplest is by using an input geometry close to that of the transition state and then iterating to a maximum energy. The second method is by selecting inputting the product and reactant molecules and labeling the corresponding atoms in each. The program can then go through the geometries linking the two structures to find that which has the highest energy.
Nf710 (talk) 16:14, 3 December 2015 (UTC)Nice intro, but some understanding of the theory here would have been nice
The Cope Rearrangement of 1,5-hexadiene
Background
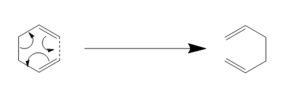
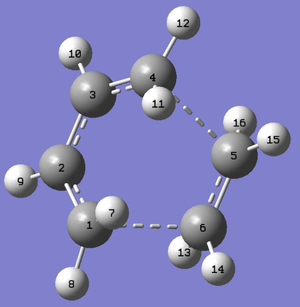
The Cope Rearrangement is an example of a sigmatropic rearrangement, this is a category of pericyclic reaction involving 1,5-dienes in which one sigma bond is formed and another is broken with electrons travelling through the pi system of the diene. In the specific case covered here, that of 1,5-hexadiene, the product formed is the same as the reactant which allows for ease of analyzing the transition state.
Optimising The Reactant
Conformers
Anti2
Firstly, 1,5-hexadiene was drawn in GaussView with an anti linkage, meaning the dihedral angle of the 4 central carbon atoms was set at 180 degrees. It was then optimised under the HF/3-21G level of theory.
Energy: -231.69253530 Hartrees
Point Group: C1
Corresponds to anti2 conformer in appendix of script.
Gauche2
A different conformer of 1,5-hexadiene was then drawn with a gauche linkage (dihedral angle=60 degrees) and optimised under the HF/3-21G level of theory.
Energy: -231.69167 Hartrees
Point Group: C2
Identified as gauche2 conformer
Gauche3
Energy: -231.69266 a.u
Point Group: C1
Identified as Gauche3 conformer.
Anti2 Reoptimisation
Energy: -231.69253530 Hartrees
Point Group: C1
Close to energy from table in Appendix 1.
It was then recalculated with DFT 6-31G* in order to compare the two methods.
Energy: -234.61171 a.u
The energy cannot be compared between the two structures as the two methods have different 'zero points' in terms of energy.
Nf710 (talk) 16:18, 3 December 2015 (UTC) This energy is correct, you didn't give a valid reason fro why the gauche 3 is the lowest in energy, its to do with secondary orbital interactions between the pi groups.
The geometries are compared in terms of bond lengths of the Carbons marked in the picture below in the table below.
| Bond Lengths (Å) | ||
|---|---|---|
| Atoms | B3LYP | HF |
| C1-C2 | 1.33352 | 1.31615 |
| C2-C3 | 1.50421 | 1.50888 |
| C3-C4 | 1.54808 | 1.55289 |
The 4-5 and 5-6 bond lengths are equal to 2-3 and 1-2 respectively by symmetry.
The central dihedral angle of both structures is exactly 180o as is expected but the outer differs between the two. For the B3LYP structure it is 118.59o but for the HF structure it is 114.67o.
Frequency Calculation
Sum of:- Electronic and zero-point energies: 234.469203
-Electronic and Thermal Energies: 234.461857
-Electronic and Thermal Enthalpies: 234.460913
-Electronic and Thermal Free Energies: 234.500777
Optimizing the "Chair" and "Boat" Transition Structures
Chair
TS Berny Method
Allyl fragment Formed and optimised
To do this method of transition state optimisation, a structure must first be formed that is close in geometry to the real transition state for the reaction. This structure is then optimised to the correct geometry using the TS Berny method under HF/3-21G level of theory. The structure formed had a vibration corresponding to the Cope Rearrangement.
Vibration at imaginary frequency of -817.93cm-1
The presence of an imaginary frequency shows the structure is at a maximum of energy and therefore that the structure is a transition state. The fact that the structure has only 1 imaginary frequency confirms that it is a true transition state rather than a saddle point. The mathematical meaning of a negative frequency demonstrates that a vibration is taking the structure to a lower energy conformation, therefore the force constant of the vibration is negative.[1]
Nf710 (talk) 16:27, 3 December 2015 (UTC) Perhaps there is some confusion here its only a negative frequency because gaussian prints it that way. its imaginary because the second derivative of the PES at at maxiumum is negative. this force constant is therefore needed in the quantum harmonic oscillator where it is square rooted and therefore becomes imaginary
Frozen Coordinate Method
Optimised again with frozen coordinate method
Bond forming length = 2.02033 Angstroms, this extremely close to the length of 2.02036 Angstroms which was found in the result structure of under the TS Berny method so we can see that both methods produce similar results.
COMPARE TO PREVIOUS OPTIMISATION STRUCTURE
Boat
QSTR1 Method
The next method used was the QSTR1 calculation, used to find the boat transition structure. This method works by drawing in the reactant and product molecules (in this case, they are the same thing) and numbering the corresponding atoms in each structure, the program then finds an intermediate structure between the two that has the highest energy, thereby generating the transition state.
The reactant and product molecules are numbered for QSTR2 calculation
The calculation failed as the conformers of each molecule were too far from the boat structure that was to be found, instead generating the structure below.
The numbering was then repeated on conformers more closely resembling the transition state.
This gave the boat transition state below.
One imaginary frequency at -839.75cm-1
Nf710 (talk) 16:35, 3 December 2015 (UTC) All your frequencies are correct for your TS structures
IRC Calculation
In order to predict which conformers are connected by a given transition state, a Intrinsic Reaction Coordinate (IRC) calculation can be done. This iterates from the transition structure, taking geometry steps down the steepest gradient in order to find a local minimum.
The calculation was done, finishing at n=44. It shows that the boat structure links gauche2 conformers.
Activation Energies
Chair
Chair TS energy=-234.55693100 Hartrees (=615,829 kJ/mol)
Ground State Energy=-234.61132602 Hartrees (=-615,972 kJ/mol)
Chair Activation Energy = 143 kJ/mol = 34.18 kcal/mol
This is close to the experimental value of 33.5±0.5 kcal/mol indicating a fairly successful calculation.
Boat
Boat TS Energy=-234.54307872 Hartrees (=-615792 kJ/mol)
Ground State Energy = -234.61132602 Hartrees (=-615,972 kJ/mol)
Boat Activation Energy = 180kJ/mol = 43.02kcal/mol
This is within the experimental range for the activation energy of 44.7±2.0 kcal/mol indicating a successful calculation
Nf710 (talk) 16:41, 3 December 2015 (UTC) you havent shown the frequencies of the B3LYP, or compared the geoms. your electronic energies are correct but you have worked out your activation energy wrong. In general a good report but you missed a few key things and you lacked knowledge of the theory.
The Diels-Alder Cycloaddition
Background
The Diels-Alder Reaction is a type of pericyclic reaction known as a cycloaddition. Cycloadditions involve the interaction of a Diene and a dienophile in which the pi orbitals on both molecules interact to form 2 new sigma bonds between the two in a concerted, stereospecific reaction.
(This isn't strictly true - there are many types of cycloaddition, which includes the Diels-Alder class of reactions Tam10 (talk) 17:38, 1 December 2015 (UTC))
The facility of this reaction is determined by the extent to which the HOMOs and LUMOs of the molecules can interact, this is determined by the closeness of the energy of the orbitals, and the overlap density, if the symmetry does not match, no reaction can occur.
The reaction of Ethene and Butadiene
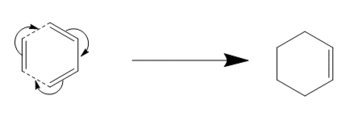
This is the simplest version of the Diels-Alder reaction. Classified as a [4s+2s] reaction[2] as the butadiene has 4 pi orbitals involved and ethene has 2. The s refers to the symmetry of those orbitals. In reality, this reaction is not particularly facile due to the fact that the butadiene must adopt the s-cis conformer, a fairly high energy conformation in order for the reaction to occur.
(The fact that butadiene has to adopt the cis conformer is not the biggest issue. The activation energy is a bit higher than the thermal energy at room temperature. The real issue is the energy of the orbitals don't match so well, which is why adding EWGs to the dienophile and EDGs to the diene help Tam10 (talk) 17:38, 1 December 2015 (UTC))
Building and optimising reactants
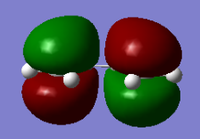
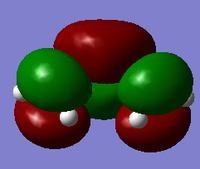
Cis-butadiene was built in GaussView and optimised under the HF/3-21G level of theory
| HOMO orbital | LUMO orbital |
|---|---|
 |
|
| Symmetric with respect to the plane | Antisymmetric with respect to the plane |
Reaction TS
Attempted to find TS by QSTR2 but did not work so done by TS Berny under SE/AM1 level of theory.
Vibration = -956.44cm-1
This vibration shows a synchronous bond formation.
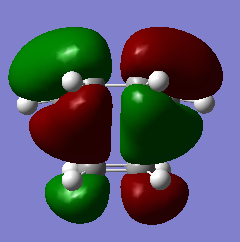
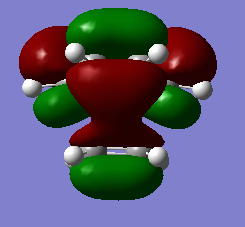
| HOMO orbital | LUMO orbital |
|---|---|
 |
|
| Anti symmetric with respect to the plane | Symmetric with respect to the plane |
By inspecting and comparing with the reactant MOs, it can be seen that the HOMO of the transition state was formed by the LUMO of Ethene and HOMO of Butadiene and the LUMO was formed by the HOMO of ethene and the LUMO of butadiene. These matches make sense as an allowed reaction as the symmetry matches for each pair as A is paired with a and S if paired with S, meeting the Woodward-Hoffman Rules for pericyclic reactions.
The Bond lengths in the transition state can be inspected to compare with typical C-C bond lengths and understand the transition structure.
The bond lengths are listed in the table below along with typical bond lengths for sp2 and sp3 C-C bonds.[3]
| Atoms | Bond Lengths (Å) |
|---|---|
| C1-C2 | 1.38185 |
| C2-C3 | 1.39740 |
| C1-C6 | 2.11932 |
| C5-C6 | 1.38293 |
| C-C | ~1.54 |
| C=C | ~1.47 |
The bonds at which a pi bond are being made or broken in the course of reaction have a bond length even shorter than that of a typical C-C pi bond, indicating some contraction of the bond in the transition state. As the Van Der Waals radius is 1.70 Angstroms, and the C1-C6 length is much less than twice that length, it can be seen that there is an interaction between these Carbons, indicating the formation of a sigma bond.
The Reaction of Maleic Anhydride and Cyclohexadiene
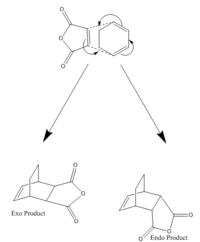
This Diels-Alder is a much more feasible reaction to carry out in real life compared to the simpler, ethene/butadiene reaction. This is due to 2 main factors, the conformation of the cyclohexadiene fixes the diene group into a cis formation which allows reaction to occur, and the electron withdrawing anhydride group on maleic anhydride increases the dienophilicity of the C-C pi bond.
The increased complexity of the reactants also allows the possibility of two reactants to be formed depending on if the maleic anhydride approaches from the top or the bottom face of the cyclohexadiene. The two products are designated as endo or exo. The endo product tends to predominate under kinetic conditions due to its lower energy transition state.[2]
Reactants
Maleic Anhydride
| HOMO orbital | LUMO orbital |
|---|---|
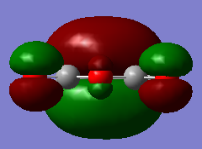 |
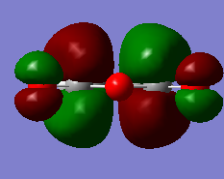
|
| Symmetric with respect to the plane | Antisymmetric with respect to the plane |
Cyclohexadiene
| HOMO orbital | LUMO orbital |
|---|---|
 |

|
| Antisymmetric with respect to the plane | Symmetric with respect to the plane |
Transition States
Exo
Energy:-0.05041968 Hartrees
Vibration=-811.99cm-1
Formed C-C sigma bond lengths, 2.17A
| HOMO orbital | LUMO orbital |
|---|---|
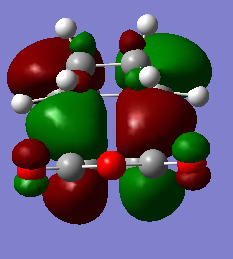 |
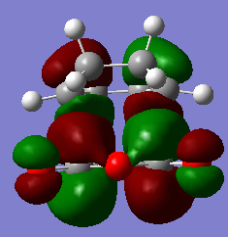
|
By inspection it can be found that the HOMO is formed by LUMO of Maleic anhydride and the HOMO of cyclobutadiene and the LUMO is formed by the HOMO of maleic anhydride and the LUMO of cyclobutadiene. Once again, this fits with expectation as the symmetries match for an allowed reaction.
Endo
Energy: -0.05150473 Hartrees
Vibration=-806.26cm-1
Formed C-C Sigma Bond lengths, 2.16A
| HOMO orbital | LUMO orbital |
|---|---|
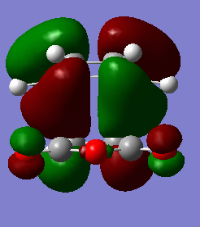 |
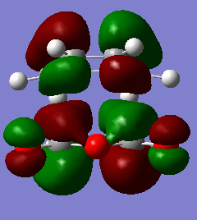
|
The HOMO and LUMO of the endo product are formed by the same MOs of the reactant molecules as the HOMO and LUMO of the exo product.
Comparison
As both were computed with SE/AM1 level of theory, the energies of the transition states can be compared . The exo transition state is 0.00108505 Hartrees higher in energy than than of the endo, this is agrees with experimental evidence that, when this reaction is done under Kinetic conditions, the endo product dominates.
One possible explanation for the higher energy of the exo transition state could be the slight increase in steric repulsion in its approach trajectory. In the exo transition state, the -(C=O)-O-(C=O)- fragment of the maleic anhydride approaches parallel to the -(CH2-CH2)- fragment on the cyclohexadiene as opposed to the -(CH-CH)- fragment it approaches in the endo transition state. The increased bulk of the extra hydrogens, as well as the fact that 2 of the hydrogens are pointed more towards it in this transition state increased its energy, therefore the activation energy of this reaction pathway.
It can be seen, in the diagram above, that in the transition state for the endo product, that the -(C=O)-O-(C=O)- fragment approaches close to the forming C-C pi bond, it is possible that there could be some favourable orbital overlap between these two systems as the maleic anhydride fragment has a great deal of pi bonding around it. This could also be an additional factor in lowering the energy of this transition state over that for the exo product. This is described as the Secondary Orbital Overlap Effect.[2]
References
- ↑ Trapp, C. A et al. Atkins' Physical Chemistry. New York, NY: W.H. Freeman and Company, 2010. Print.
- ↑ 2.0 2.1 2.2 Clayden, Jonathan. Organic Chemistry. Oxford: Oxford University Press, 2001. Print.
- ↑ http://www.masterorganicchemistry.com/2010/10/13/sigma-bonds-come-in-six-varieties-pi-bonds-come-in-one/