Jump to content

Rep:Mod:kwlittle2

From ChemWiki

Cope Rearrangement

Optimising reactants and products

In Gaussview, a molecule of 1,5-hexadiene in the 'anti' conformation was drawn by placing an ethyl fragment and replacing anti-periplanar hydrogen atoms with vinyl fragments, then optimised using the Hartree-Fock method, 3-21G basis set[1]. A 'gauche' molecule was drawn by replacing a benzene ring fragment's atoms with methyl and vinyl fragmets, then optimised[2].

I predicted that the lowest-energy conformer would be similar to the gauche conformer but with the central dihedral angle at 180 ('anti3' in the appendix table); both this and 'anti2' were drawn and optimised[3][4]. The energies and symmetries of all these molecules are:

Conformation Point Group Energy / au
gauche C2 -231.68771613
anti C2h -231.69253525
anti2 Ci -231.69253529
anti3 C2h -231.68907062

The anti2 molecule was re-optimised[5] using the B3LYP method and 6-31G* basis set, to give an energy of -234.61171035 au and slightly larger C-C-C angles. This optimised molecule was submitted for frequency analysis at STP[6] and at absolute zero[7] (actually at 0.01K, as Gaussian would not calculate 0K) to give specific energy terms:

Energies of 'anti2' 1,5-hexadiene in Hartrees
Energy type 298.15K 0K
Sum of electronic and zero-point Energies -234.469204 -234.469204
Sum of electronic and thermal Energies -234.461857 -234.469203
Sum of electronic and thermal Enthalpies -234.460913 -234.469203
Sum of electronic and thermal Free Energies -234.500777 -234.469203

Gaussian output files

  1. ↑ File:ANTIHF.LOG
  2. ↑ File:GAUCHEHF.LOG
  3. ↑ File:ANTI3HF.LOG
  4. ↑ File:ANTI2HF.LOG
  5. ↑ File:ANTI26-31G.LOG
  6. ↑ File:ANTI2FREQ.LOG
  7. ↑ File:ANTI2FREQ0K.LOG

Optimising the chair and boat transition structures

The chair transition state.
The boat transition state.

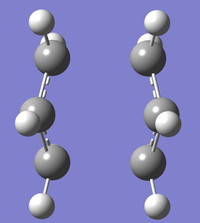
Chair

An allyl fragment was drawn in GaussView and optimised with the HF/3-21G method[1]. This was duplicated, and one of the fragments rotated to make an approximation of the chair transition state. The true transition structure was found from this via two different methods, each using the HF/3-21G method:

First, the approximate structure was simply optimised to a Berny Transition State with the HF/3-21G method[2], calculating force constants once, to give a molecule with a single imaginary vibration a -818cm-1.

The approximate structure was also optimised to a minimum, but with modified 'redundant coordinates'. Two coordinate systems were set: each with two carbon atoms at the end of either allyl fragment as a 'Frozen Bond' coordinate, and 'opt=ModRedundant' was added to the keywords. This failed initially as only a single frozen coordinate was set, making an asymmetrical molecule. This was corrected to give a true optimised molecule[3]. This was then optimised to a transition state[4] without calculating force constants, but with the redundant coordinates changed to 'Bond Add' type.

These two methods produce equivalent transition structures, both with forming/breaking bond lengths of 2.02A and C-C bond lengths of 1.39A.

Boat

The boat structure was found by the QST2 method, which interpolates between a reactant and product. In this case, the two are the same but with different atom numbering representing the changed bond structure. The optimised 'anti2' conformer was opened, then copied and pasted as a second molecule in the same group. The atom labelling of the second molecule was changed, and the group submitted for optimisation to a QST2 transition state with HF/3-21G method[5].

This first optimisation failed, giving a structure similar to the chair transition state. The original molecule group was opened, then the central dihedral angle of each molecule changed to 0 and the central C-C-C angles changed to 100, making them similar to the 'gauche2' conformer. This was optimised but failed, giving a twist-boat-like structure[6]. The optimisation was repeated, this time calculating force constants once, which went to completion to produce the boat transition state[7].

Intrinsic reaction coordinate

By inspection, the chair transition structure looks as if it will form the gauche conformer of 1,5-hexadiene. This was tested by the Intrinsic Reaction Coordinate method, which follows the reaction from the transition state to its products or reactants. The chair structure as calculated by the TS(Berny) force constants method was opened and submitted for IRC, calculating force constants once and setting the maximum cycles to 100[8]. This calculation failed, stating "Maximum number of corrector steps exceded"; however, the final molecule produced looked close to the gauche2 conformer.

This was confirmed in two ways: by optimising this outputted molecule to a minimum[9] at the B3LYP/6-31G* level, and also by repeating the IRC method, calculating force constants at each step[10] and then optimising the final molecule as above[11]. Both methods produced equivalent gauche2 conformers.

Activation energies

The activation energies of the reaction for the anti2 conformer were calculated by taking the difference between its energy and that of each transition state at both the HF/3-21G and B3LYP/6-31G* levels of theory.

All energies in Hartrees
Theory anti2 chair Ea(chair) boat Ea(boat)
HF/3-21G -231.69253529 -231.61932232 0.073213 -231.60280203 0.089733
HF/3-21G (electronic and thermal free energies) -231.570913 -231.495206 0.075707 -231.479773 0.09114
B3LYP/6-31G* -234.61171035 -234.55698303 0.054727 -234.54309307 0.068617
B3LYP/6-31G* (electronic and thermal free energies) -234.500777 -234.443814 0.056963 -234.431752 0.069025

These activation energies in kcal/mol are:

Theory Ea(chair) Ea(boat)
HF/3-21G 0K 45.94183193 56.30847033
HF/3-21G 298.15K 45.94183193 57.19121300
B3LYP/6-31G* 0K 34.34191151 43.05799294
B3LYP/6-31G* 298.15K 35.74482188 43.31384110
Experimental 33.5 ± 0.5 44.7 ± 2.0

Thus, the computationally-calculated energies closest to experiment are those using the B3LYP method, 6-31G* basis set and with thermal corrections.

Gaussian output files

  1. ↑ File:ALLYL.LOG
  2. ↑ File:CHAIRFORCE.LOG
  3. ↑ File:CHAIRFROZEN3.LOG
  4. ↑ File:CHAIRFROZENTS.LOG
  5. ↑ File:CHAIRQST2.LOG
  6. ↑ File:CHAIRQST2MOD.LOG
  7. ↑ File:CHAIRQST2MOD3.LOG
  8. ↑ File:CHAIRIRCONCE.LOG
  9. ↑ File:CHAIRIRCOPT.LOG
  10. ↑ File:CHAIRIRCALWAYS.LOG
  11. ↑ File:CHAIRIRCALWAYSOPT.LOG

The Diels-Alder cycloaddition

Cisbutadiene

A cis-butadiene molecule was drawn in Gaussview and optimised using the AM1 molecular orbital method,[1], giving a planar structure (interestingly, optimising with B3LYP/6-31G* breaks symmetry and distorts the molecule from planarity). The molecular orbitals were visualised and the HOMO and LUMO plotted:

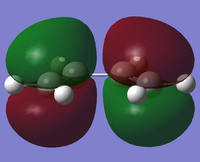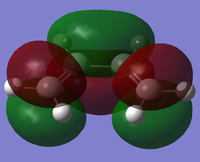The two pi bonds are distinct, not forming a single delocalised system across the whole molecule at the HOMO. The HOMO is antisymmetric with respect to both the plane of the molecule and the central σv plane; the LUMO is symmetric with respect to the plane of the molecule but not the σv plane.

Cisbutadiene ethene reaction

Click to see an animation of the reaction.

Cis-butadiene undergoes a Diels-Alder reaction with ethene to form cyclohexene. A guess transition state for this reaction was drawn by placing a bicyclo[2.2.2]octane fragment in GaussView, removing two CH2 fragments and removing two hydrogens to create the double bond. The redundant coordinate method was used to find the optimised transition state, which was then further optimised with the HF/3-21G method[2][3], giving a transition structure with a single imaginary frequency of -818. Note that using a different method from cisbutadiene means that energies and exact sizes and shapes of the molecular orbitals cannot be compared; however, the symmetries and general shape of these simple molecular orbitals can be compared. The HOMO and LUMO of the transition state are:

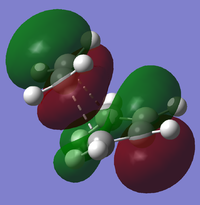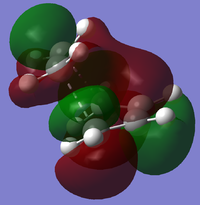The forming/breaking bonds have a length of 2.20A, and the other C-C bonds in the transition structure are 1.37-1.39A. Typical C-C bond lengths are around 1.54A for sp3 bonds and 1.35A for sp2.

The HOMO of the transition structure is symmetrical with respect to the σv plane and to the bond planes of each reactant molecule, whereas the LUMO is asymmetrical with respect to the bonding planes. This suggests that the HOMO of ethane is interacting with the LUMO of cisbutadiene to form the transition state HOMO, showing the fact that reactions in which a HOMO and LUMO of the same symmetry interact are allowed.

Cyclohexa-1,3-diene maleic anhydride reaction

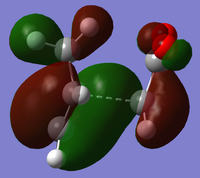
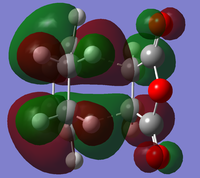
The optimised transition state for the cisbutadiene ethene reaction was modified to form guess structures for both the exo and endo transition states for the cyclohexa-1,3-diene maleic anhydride reaction. These were optimised to the transition state using the redundant coordinates method, as simple optimisation calculating force constants failed: for the exo transition state, the minimum was found using AM1 and then optimised to a transition state using HF/3-21G[4][5]. Its HOMO and LUMO are:

HOMO
HOMO
LUMO
LUMO

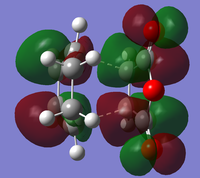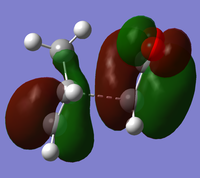
The endo minimisation initially failed. Measuring the bond forming/breaking lengths of around 2.2A in the endo transition state and fixing the redundant coordinate bonds at this length allowed the minimisation to complete; the transition state optimisation then had to be carried out using AM1 before reoptimisation using HF/3-21G[6][7][8], to give these HOMO and LUMO:

HOMO
HOMO
LUMO
LUMO

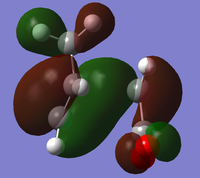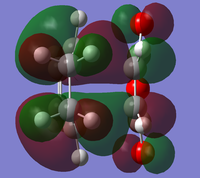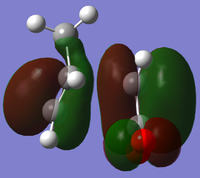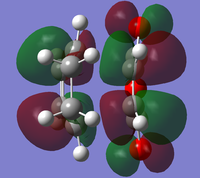At the HF/3-21G level, the energy of the exo form is -605.60359125 a.u. and of the endo form is -605.61036734 a.u. This suggests that under thermodynamic control, the endo product will dominate. To understand this energy difference, the structural differences and electronic differences in the HOMOs between the two transition states must be considered:

All distances in Angstrom
Transition State Breaking/forming bond distance Through-space distance Maleic C=C distance Cyclohexadiene C=C distance Cyclohexadiene C-C distance
exo 2.26 2.92 1.37 1.37 1.40
endo 2.23 2.85 1.37 1.37 1.40

Note that 'through space distance' above refers to that between the maleic anhydride carbonyl carbon atoms, and the carbon atoms on the opposing -CH2-CH2- or -CH=CH- group; the 'cyclohexadiene C-C distance' refers to the single bond between the two central sp2 carbons, where a new double bond is forming.

There is no difference in the lengths of the existing bonds which are changing, but the exo form has longer forming bonds, which are thus further from the ideal length and require more energy to create. The 'through-space distance' between carbon atoms is further, but not to the hydrogen atoms on the -CH2-CH2- fragment (2.43A), this it is possible that there is more repulsion here; however, this is difficult to draw a conclusion from, so the HOMOs must be considered.

The HOMOs of the two forms are very similar, with the pi systems of the cyclohexa-1,5-diene and maleic anhydride C=C interacting and a nodal plane down the molecule's central plane of symmetry. The most significant difference is that the pi system of the -(C=O)-O-(C=O)- has a bonding interaction with the opposite pi system in the exo form, whereas in the endo form there is a close antibonding interaction. From the structures it is difficult to determine why the endo form is favoured.

Gaussian output files

  1. ↑ File:BUTADIENE.LOG
  2. ↑ File:ETHENEBUTADIENEFREEZE.LOG
  3. ↑ File:ETHENEBUTADIENEFREEZETSHF.LOG
  4. ↑ File:MALEICEXOFREEZE.LOG
  5. ↑ File:MALEICEXOFREEZETS3.LOG
  6. ↑ File:MALEICENDOFREEZEAM1.LOG
  7. ↑ File:MALEICENDOFREEZETSAM1.LOG
  8. ↑ File:MALEICENDOFREEZETSHF.LOG
Retrieved from "https://chemwiki.ch.ic.ac.uk/index.php?title=Rep:Mod:kwlittle2&oldid=819984"