Rep:Mod:ks4817
NH3
Information about the molecule
| Name | Ammonia |
| Calculation Method | RB3LYP |
| Basis Set | 6-31G(d.p) |
| Final Energy (au) | -56.55776873 |
| RMS Gradient(au) | 0.00000485 |
| Point Group | C3V |
| Optimized Bond Distance (au) | 1.01798 |
| Optimized Bond Angle (degrees) | 105.741 |
Item Table
Item Value Threshold Converged? Maximum Force 0.000004 0.000450 YES RMS Force 0.000004 0.000300 YES Maximum Displacement 0.000072 0.001800 YES RMS Displacement 0.000035 0.001200 YES
Image
Optimized Ammonia Molecule Structure |
Vibrations
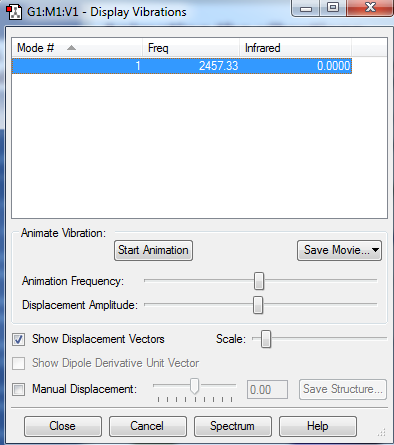
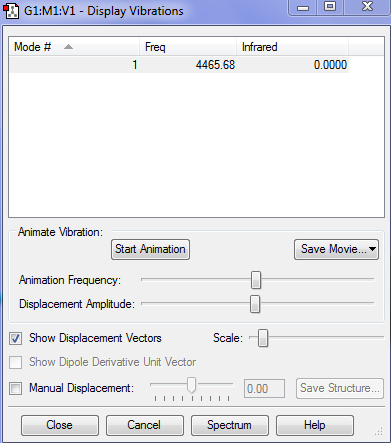
There are 6 different Vibrations, with the 3N-6 rule for vibrations which we use for non linear molecules we expect 6 since there are 4 atoms. These vibrations can be seen in the image and table bellow:
| Vibration # | Image | Type of Vibration |
|---|---|---|
| 1 | 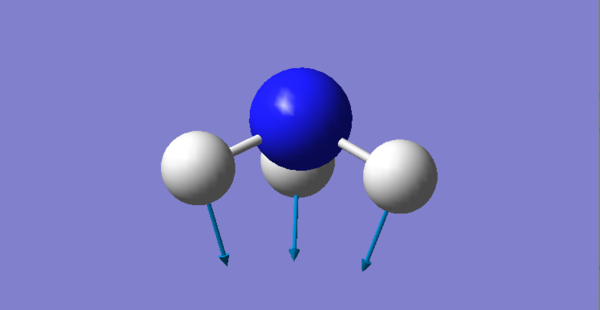 |
Bending |
| 2 |  |
Bending |
| 3 | 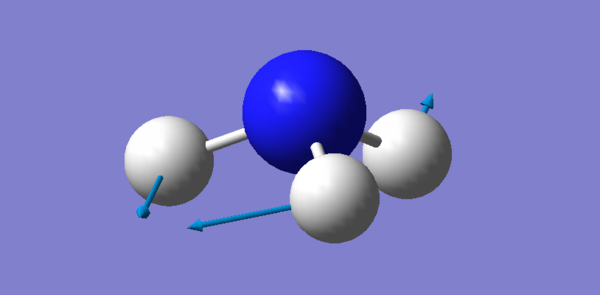 |
Bending |
| 4 | 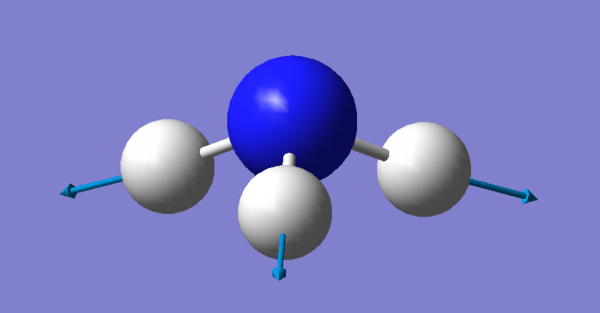 |
Stretching |
| 5 | 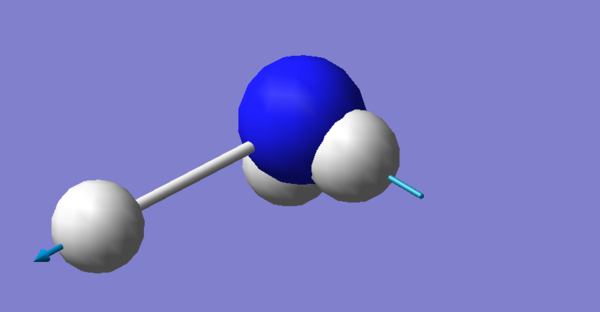 |
Stretching |
| 6 |  |
Stretching |
There are two pairs which have the same energy: Modes 2 and 3 have the same energy, as they have the same frequency, and Mode 5 and 6. The highly symmetric mode is 4. The umbrella mode is 1. In an experimental spectrum of gaseous ammonia you would expect 4 bands.
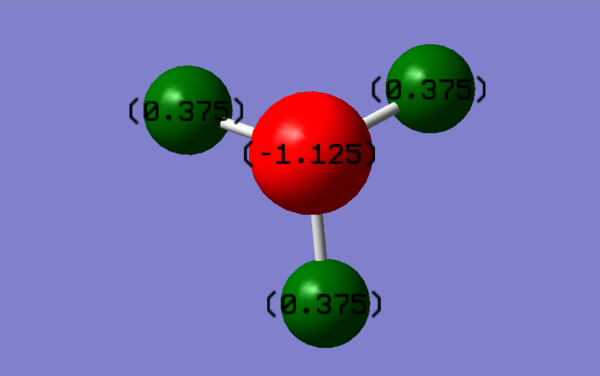
Charge Distribution
The charges can be seen in the picture bellow. The charge on the N is -1.125 and the charge on the H's is 0.375. This is expected because the Nitrogen is more electronegative compared to the Hydrogen's therefore it would have a slightly negative charge as it pulls the electron density closer to itself.
N2
Information about the molecule
| Name | Nitrogen |
| Calculation Method | RB3LYP |
| Basis Set | 6-31G(d.p) |
| Final Energy (au) | -109.52412868 |
| RMS Gradient(au) | 0.00000060 |
| Point Group | D∞h |
| Optimized Bond Distance (au) | 1.10550 |
| Optimized Bond Angle (degrees) | 180 |
Item Table
Item Value Threshold Converged? Maximum Force 0.000001 0.000450 YES RMS Force 0.000001 0.000300 YES Maximum Displacement 0.000000 0.001800 YES RMS Displacement 0.000000 0.001200 YES
Image
Optimized Nitrogen Molecule Structure |
Vibrations
Because it is a linear molecule, Nitrogen (according to the 3N-5 rule for linear molecules) only has one vibration. This vibration is a stretch vibration and is not IR active because during the stretch there is no change in dipole moment.

H2
Information about the molecule
| Name | Hydrogen |
| Calculation Method | RB3LYP |
| Basis Set | 6-31G(d.p) |
| Final Energy (au) | -1.17853936 |
| RMS Gradient(au) | 0.00000017 |
| Point Group | D∞h |
| Optimized Bond Distance (au) | 0.74279 |
| Optimized Bond Angle (degrees) | 180 |
Item Table
Item Value Threshold Converged? Maximum Force 0.000000 0.000450 YES RMS Force 0.000000 0.000300 YES Maximum Displacement 0.000000 0.001800 YES RMS Displacement 0.000001 0.001200 YES
Image
Optimized Hydrogen Molecule Structure |
Vibrations
Similarly to nitrogen: hydrogen only has one vibration, it is a stretch vibration and it's not IR active because during the stretch there is no change in dipole moment.

Energy Calculations for NH3
N2 + 3H2 => 2NH3
The values in the table bellow are shown in au.
| E(NH3) | -56.55776873 |
| 2xE(NH3) | -113.11553746 |
| E(N2) | -109.52412868 |
| E(H2) | -1.17853936 |
| 3xE(H2) | -3.53561808 |
| ΔE=2xE(NH3)-(E(N2)+3xE(H2)) | -0.0557907 |
The ΔE in kJmol-1 is -146.464535175 which can be simplified to -146.46 kJmol-1 (2 d.p.). This is the energy for converting nitrogen and hydrogen into ammonia gas. As the change in energy is negative this would imply that the ammonia is more stable compared to the hydrogen and nitrogen.
ClF
Information about the molecule
| Name | Chlorine Monofluoride |
| Calculation Method | RB3LYP |
| Basis Set | 6-31G(d.p) |
| Final Energy (au) | -559.94269578 |
| RMS Gradient(au) | 0.00014211 |
| Point Group | C∞V |
| Optimized Bond Distance (au) | 1.66434 |
| Optimized Bond Angle (degrees) | 180 |
Item Table
Item Value Threshold Converged? Maximum Force 0.000246 0.000450 YES RMS Force 0.000246 0.000300 YES Maximum Displacement 0.000433 0.001800 YES RMS Displacement 0.000613 0.001200 YES
Image
Optimized ClF Molecule Structure |
Vibrations
There is one vibration, this corresponds to the theory as the number of vibrations for a linear molecule is 3N-5, so if there are 2 atoms there is only 1 vibration. This vibration is a stretch and seeing as how there is a change in dipole moment the molecule is IR active. The Cl has a smaller vector of vibration than the F because it is a heavier atom.

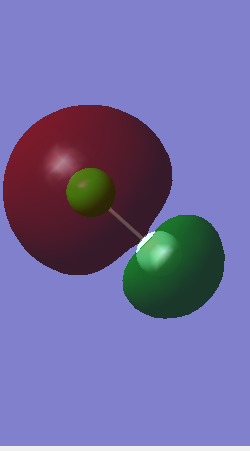
Charge Distribution
The atom shown in red with the negative charge is Fluorine and the atom shown in green with the positive charge is Chlorine. The linear molecule overall has no charge however there is a negative dipole generated on fluroine. Although both atoms are very electronegative, Fluorine because of its smaller size and less shielding of its positive charge is more electronegative therefore it pulls the electron density towards itself.The positive and negative values are equal because whatever negative electron density fluorine gains, chlorine looses.

Molecular Orbitals
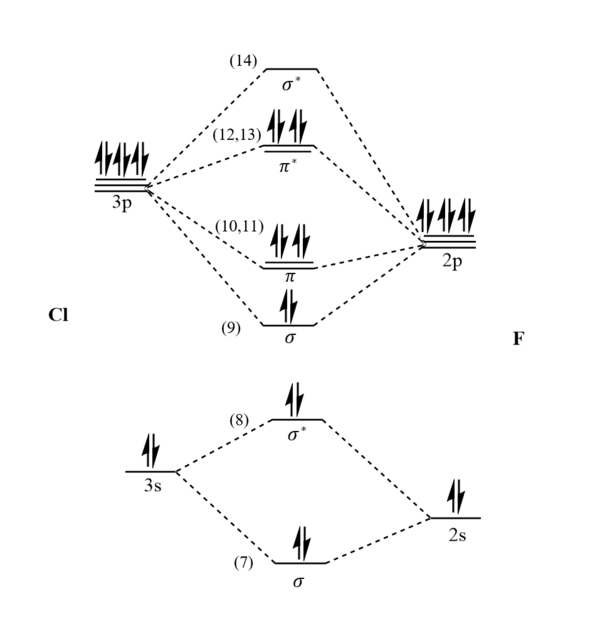
The list of orbitals generated by Gaussview can be seen bellow:

Only Orbitals 1-14 were examined as they represent the lowest energy orbitals, orbitals of higher energy did not contain electrons and there was large uncertainty in their shapes. Orbitals 1-6 were determined to be the shapes of the core atomic orbitals, which do not participate in bonding. Starting from Orbital 7 the molecular orbitals began to appear, these were then examined more closely. In all the screenshots of the molecular orbitals bellow the Cl is shown as the green molecule on the left and F is the blue molecule on the right. A molecular orbital diagram can be drawn from theory which can help identify the molecular orbitals seen bellow:
Orbital 7

Looking at the molecular orbital diagram this appears to be an in-phase overlap (bonding orbital) of the 3s orbital on the Cl and the 2s orbital on the F because it is the molecular orbital with the lowest energy. Moreover it appears to have a combined shape of two spherical s orbitals. This overlap would form a σ bond between the molecules if the corresponding anti-bonding orbital was not occupied (however the anti-bonding orbital does contain electrons: Orbital 8). The orbital according to Gaussview and the molecular orbital theory wold be occupied with two electrons. This orbital is deep in energy but not as deep compared to the atomic Orbital 1.
Orbital 8
The next molecular orbital which has the lowest energy appears to be the out of phase overlap (anti-bonding orbital) of the 3s orbital and the 2s orbital on the Cl and F respectively. There is an angular node in the center of the orbitals where the two wave equations would cancel each other out. This orbital according to Gaussview and the molecular orbital theory would be occupied with 2 electrons therefore orbital 8 (it's corresponding bonding orbital) has little effect on the final outcome of the bonding. It is also much higher in energy according to Gaussview than orbital 7.
Orbital 9
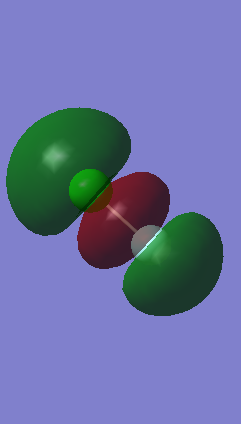
Orbital 9 is the in phase orbital overlap of the 3pz and 2pz orbitals. The two orbitals are face each other and therefore when they overlap the two in phase lobes form a larger electron density surface in the center of the two atoms. This would correspond to a σ bonding orbital which according to both theory and Gaussview is occupied with two electrons. Moreover its corresponding anti-bonding orbital (Orbital 14) is unoccupied meaning that this orbital contributes to the final bonding structure. This is why there is only one sigma bond between the two atoms. This atomic orbital is again higher in energy than Orbital 8 as we can see on the Gaussview generated list and on the sketch of the molecular orbital energies however the difference between the two energies decreases as we go up and the energy levels converge. It is lower in energy than the other p molecular orbitals because it is orientated along the bond.
Orbitals 10 and 11


Orbitals 10 and 11 are degenerate orbitals as can be seen in the energies calculated by Gaussview. They both have the same shape but a different orientation in space. According to theory one is the in phase overlap 3px and 2px the other of 3py and 2py, depending on what orientation in space these axes were assigned. However these overlaps are not a direct overlaps, it is caused by the orbitals being next to each other. They are both occupied with 2 electrons each. This would make them bonding orbitals corresponding to π bonds, nevertheless they have no effect on the final bonding because their anti bonding orbitals (Orbitals 12 and 13) also contain electrons. These are higher in energy than all the orbitals that came before it and once again the difference between energy levels decreases.
Orbitals 12 and 13


Orbitals 12 and 13 both are also degenerate orbitals, again only differing in orientation in space. They are the anti-bonding orbitals corresponding to the orbitals 10 and 11, formed through the out of phase interaction between a 3px and a 2px or a 3py and a 2py. With the out of phase orbitals being placed next to each other an angular node between them is formed. They are both occupied with 2 electrons each. These orbitals are also the HOMOs.
Orbital 14

Orbital 14 is the anti-bonding orbital corresponding to orbital 9. The two out of phase lobes overlap directly in the center of the bond creating two small lobes in the center of the bond. However this orbital is unoccupied, according to both Gaussview and Molecular orbital theory, which means that its corresponding bonding orbital 9 contributes to the bond. This is why the two atoms are bonded with one sigma bond. This molecular orbital would also be the LUMO of the molecule.
Energy Calculations for ClF
Cl2
Information about the molecule
| Name | Chlorine |
| Calculation Method | RB3LYP |
| Basis Set | 6-31G(d.p) |
| Final Energy (au) | -920.34987886 |
| RMS Gradient(au) | 0.00002511 |
| Point Group | D∞h |
| Optimized Bond Distance (au) | 2.04174 |
| Optimized Bond Angle (degrees) | 180 |
Item Table
Item Value Threshold Converged? Maximum Force 0.000043 0.000450 YES RMS Force 0.000043 0.000300 YES Maximum Displacement 0.000121 0.001800 YES RMS Displacement 0.000172 0.001200 YES
Image
Optimized ClF Molecule Structure |
Vibrations
Again this is a linear molecule with 1 stretch vibration and it's not IR active.


F2
Information about the molecule
| Name | Fluorine |
| Calculation Method | RB3LYP |
| Basis Set | 6-31G(d.p) |
| Final Energy (au) | -199.49825218 |
| RMS Gradient(au) | 0.00007365 |
| Point Group | D∞h |
| Optimized Bond Distance (au) | 1.40281 |
| Optimized Bond Angle (degrees) | 180 |
Item Table
Item Value Threshold Converged? Maximum Force 0.000128 0.000450 YES RMS Force 0.000128 0.000300 YES Maximum Displacement 0.000156 0.001800 YES RMS Displacement 0.000221 0.001200 YES
Image
Optimized ClF Molecule Structure |
Vibrations
Again this is a linear molecule with 1 stretch vibration and it's not IR active.

Energy Calculations
Cl2 + F2 => 2ClF
The energies shown in the table bellow are in au:
| E(ClF) | -559.94269578 |
| 2xE(ClF) | -1119.88539156 |
| E(Cl2) | -920.34987886 |
| E(F2) | -199.49825218 |
| ΔE=2xE(ClF)-(E(Cl2)+E(F2)) | -0.03726052 |
The change in energy in kJmol-1 is -97.82749526 and when simplified this would be -97.83 kJmol-1 (2 d.p.). This would make the products more stable than the reactants because of the negative value.
