Rep:Mod:knt11miniproject
Third year Inorganic Computational Laboratory - Mini Project
Name: Kai Ni Teh
CID: 00697229
Title: Ionic Liquids and Designer Solvents
Introduction
Ionic liquids are ions which exist in the liquid form at room temperature. They are usually made up of a bulky and charged delocalised organic cation and inorganic anion. Given their vast applicability in scientific research, for instance as versatile solvents, their chemical and physical properties are of great interest. However, it is impractical and impossible to synthesise them all due to a large number of possible combinations. Hence, this computational study aims to investigate selected properties of some related cations. The first part of the study compares selected 'onium' cations and the second part investigates the influence of functional groups.
All calculations are performed based on DFT RB3LYP/6-31G(d,p) with the keyword "nosymm" as the initial optimisation and frequency computations were not converged without the keyword "nosymm".
Data and Analysis of [N(CH3)4]+
Optimisation, frequency, population and NBO analysis were performed for [N(CH3)4]+ and the data then analysed.
Optimisation
The data from the optimisation calculation are shown below.
| File type | .log |
| Calculation type | FOPT |
| Calculation method | RB3LYP |
| Basis set | 6-31G(d,p) |
| Charge | 1 |
| Spin | Singlet |
| Final energy /au | -214.1812726 |
| RMS Gradient /au | 0.00002102 |
| Dipole moment /D | 17.64 |
| Point group | C1 |
| Calculation time | 3 minutes 24.6 seconds |
Table 1. Optimisation (6-31G;d,p) data of [N(CH3)4]+.
The optimisation job is complete as the RMS gradient obtained is 0.00002102, which is less than 0.001 and close to 0. The final energy obtained is -214.1812726 au.
Item Value Threshold Converged?
Maximum Force 0.000074 0.000450 YES
RMS Force 0.000017 0.000300 YES
Maximum Displacement 0.001351 0.001800 YES
RMS Displacement 0.000368 0.001200 YES
Predicted change in Energy=-5.616101D-08
Optimization completed.
-- Stationary point found.
The optimisation job is converged. The force and displacement values are within the threshold.
Frequency
The data from the frequency calculation are shown below.
| File type | .log |
| Calculation type | FREQ |
| Calculation method | RB3LYP |
| Basis set | 6-31G(d,p) |
| Charge | 1 |
| Spin | Singlet |
| Final energy /au | -214.1812726 |
| RMS Gradient /au | 0.00002103 |
| Dipole moment /D | 17.64 |
| Point group | C1 |
| Calculation time | 7 minutes 58.9 seconds |
Table 2. Frequency (6-31G;d,p) data of [N(CH3)4]+.
The frequency job is complete as the RMS gradient obtained is 0.00002103, which is less than 0.001 and close to 0; it is also very close to that obtained from the optimisation job. The final energy obtained is -214.1812726 au, which is identical to the value obtained from the optimisation job. The dipole moment of 17.64 D is also identical to that obtained from the optimisation job.
Item Value Threshold Converged? Maximum Force 0.000073 0.000450 YES RMS Force 0.000021 0.000300 YES Maximum Displacement 0.000771 0.001800 YES RMS Displacement 0.000262 0.001200 YES Predicted change in Energy=-5.036454D-08 Optimization completed. -- Stationary point found.
The frequency job is converged. The force and displacement values are within the threshold.
Low frequencies --- -13.0360 0.0002 0.0006 0.0010 6.1792 12.0051 Low frequencies --- 179.9126 278.8725 285.7233
The first line of "low frequencies" have values within ± 26 cm-1. Although the range is larger than expected, it is acceptable as the method and basis set used are not sufficient. To obtain a smaller range of "low frequencies", a better basis set or additional keywords, such as "int=ultrafine scf=conver=9", and tighter convergence criteria can be used. The second line of "low frequencies" have only positive values, which are about one order of magnitude larger than the first line values. Overall, the frequency job is complete.
Population analysis
The data from the population analysis are shown below.
| File type | .log |
| Calculation type | SP |
| Calculation method | RB3LYP |
| Basis set | 6-31G(d,p) |
| Charge | 1 |
| Spin | Singlet |
| Final energy /au | -214.1812726 |
| RMS Gradient /au | - |
| Dipole moment /D | 17.64 |
| Point group | C1 |
| Calculation time | 1 minute 27.8 seconds |
Table 3. MO (6-31G;d,p) data of [N(CH3)4]+.
The final energy and dipole moment obtained are -214.1812726 au and 17.64 D respectively, which are identical to those of the optimisation and frequency jobs.
Further MO analysis is presented below.
| Image of MO | (Number) Energy of MO | Nature of MO | Description | |
|---|---|---|---|---|
| 1 |  |
(6) -1.19637 | Highly bonding | The hydrogen atoms do not participate in bonding or anti-bonding interactions in this MO. The C-N bonding interactions are formed through s AO interactions between the nitrogen atom and C1, C5, C9 and C13. The through bond interactions between s AOs are strong and the MO is highly delocalised throughout the entire structure. This means that the through space interactions are also relatively strong. There is no node in the structure and this MO is highly bonding in nature. |
| 2 |  |
(10) -0.80743 | Bonding | Within each methyl group, the hydrogen s AO interacts with the carbon p AO to form a strong, delocalised bonding structure, for example, the green structure between H14, H15 and H16. The p AO of each carbon interacts with the nitrogen s AO and this gives rise to a bonding interaction and there is a node between each carbon and nitrogen atoms, so there are 4 nodes in total. Through space interaction within each methyl group is relatively strong but that between the methyl groups are weak, and hence the "green" parts of the MO are not delocalised throughout the structure. Overall, there are more and stronger bonding interactions than there are anti-bonding interactions, so the structure is predominantly bonding in nature. |
| 3 |  |
(14) -0.62247 | Non-bonding | In this MO, the nitrogen atom participates in neither the bonding nor anti-bonding interactions and there is a node on the nitrogen atom. Since [N(CH3)4]+ is a tetrahedral and symmetrical molecule, the s AO of one hydrogen in each methyl group, for example, H4 or H6, forms a strong bonding interaction with the p AO of the carbon atom. The s AOs of H4, H6, H11 and H15 interact through-space to form a small delocalised structure (red). The s AOs of the remaining two hydrogen in each methyl group, for example, H7 and H8, form a strong bonding interaction with the other lobe of the p AO of the carbon atom, for example, C5. Two hydrogen atoms in each methyl group form a relatively strong through space bonding interaction with 2 hydrogen atoms from another methyl group, for instance between H7, H8 and H10, H12. There is a large node at the nitrogen atom where the possibility of finding electron density is 0. There are 4 other nodes in this MO, one each on the carbon atoms. The through space anti-bonding interactions are rather strong due to the proximity of the red and green bonding structures or groups. Overall, there is about the same amount of bonding interactions as there are anti-bonding ones. |
| 4 |  |
(17) -0.58035 | Anti-bonding | The nitrogen atom, H6 and H11 do not participate in bonding or anti-bonding interactions in this MO. For the two methyl groups containing H6 and H11, the p AO of the carbon atom forms 2 separate bonding interactions with the s AO of the two hydrogen atoms. This then results in strong through-space anti-bonding interactions due to the proximity of the hydrogen atoms within a methyl group. For the other two methyl groups containing H4 and H15, the p AO of the carbon atom forms a bonding interaction with the s AO of two hydrogen atoms using the same lobe of the p AO and a bonding interaction with the s AO of the last hydrogen atom (H4 or H15). In general, the through bond interactions in this MO are rather strong but the through space bonding interactions are very weak or negligible. In contrast, the through space anti-bonding interactions are quite strong due to the proximity of the hydrogen atoms within a methyl group. Since there are more and stronger through space anti-bonding interactions, this MO is anti-bonding in nature. |
| 5 |  |
(21) -0.57929 | Highly anti-bonding | The s AO of each of H6, H7 and H8 forms a relatively strong bonding interaction with the p AO of C5. The other lobe of the p AO of C5 then forms a bonding interaction with the p AO of nitrogen. The other lobe of this p AO of nitrogen forms bonding interactions with p AO of C1, C9 and C13. And the p AO of C1, C9 and C13 then forms bonding interactions with s AO of H3, H4, H10, H12, H15 and H16. The bonding interactions between nitrogen, carbons and hydrogens form a delocalised bonding group (red). The through space interactions within this delocalised structure are rather strong. The remaining 3 hydrogen atoms, H2, H11 and H14, form bonding interactions, using their s AO, with the p AO of carbon atoms to form a strong delocalised structure (green) with strong through space interactions. There is one node on each carbon atom and one on the nitrogen atom; thus, there are 5 nodes in total. Due to the use of many p orbitals and many phase changes, this MO is highly anti-bonding in nature. |
Table 4. MO description of [N(CH3)4]+.
Data and Analysis of [P(CH3)4]+
Optimisation, frequency, population and NBO analysis are performed for [P(CH3)4]+ and the data then analysed.
Optimisation
The data from the optimisation calculation are shown below.
| File type | .log |
| Calculation type | FOPT |
| Calculation method | RB3LYP |
| Basis set | 6-31G(d,p) |
| Charge | 1 |
| Spin | Singlet |
| Final energy /au | -500.8270031 |
| RMS Gradient /au | 0.00002556 |
| Dipole moment /D | 17.64 |
| Point group | C1 |
| Calculation time | 5 minutes 33.0 seconds |
Table 5. Optimisation (6-31G;d,p) data of [P(CH3)4]+.
The optimisation job is complete as the RMS gradient obtained is 0.00002556, which is less than 0.001 and close to 0. The final energy obtained is -500.8270031 au.
Item Value Threshold Converged?
Maximum Force 0.000148 0.000450 YES
RMS Force 0.000033 0.000300 YES
Maximum Displacement 0.000899 0.001800 YES
RMS Displacement 0.000305 0.001200 YES
Predicted change in Energy=-1.785018D-07
Optimization completed.
-- Stationary point found.
The optimisation job is converged. The force and displacement values are within the threshold.
Frequency
The data from the frequency calculation are shown below.
| File type | .log |
| Calculation type | FREQ |
| Calculation method | RB3LYP |
| Basis set | 6-31G(d,p) |
| Charge | 1 |
| Spin | Singlet |
| Final energy /au | -500.8270031 |
| RMS Gradient /au | 0.00002559 |
| Dipole moment /D | 17.64 |
| Point group | C1 |
| Calculation time | 7 minutes 40.4 seconds |
Table 6. Frequency (6-31G;d,p) data of [P(CH3)4]+.
The frequency job is complete as the RMS gradient obtained is 0.00002559, which is less than 0.001 and close to 0; it is also very close to that obtained from the optimisation job. The final energy obtained is -500.8270031 au, which is identical to the value obtained from the optimisation job. The dipole moment of 17.64 D is also identical to that obtained from the optimisation job.
Item Value Threshold Converged? Maximum Force 0.000066 0.000450 YES RMS Force 0.000026 0.000300 YES Maximum Displacement 0.006479 0.001800 NO RMS Displacement 0.002121 0.001200 NO Predicted change in Energy=-3.388912D-07
The frequency job is not converged. The force values are within the threshold but the displacement values are not and this could be due to the presence of a very gentle potential energy surface. As a result, it can be hard to distinguish whether the displacement values have converged. However, to further confirm the validity of this frequency job, the "low frequencies" values need to be assessed.
Low frequencies --- -16.5089 0.0027 0.0028 0.0029 4.9757 16.2276 Low frequencies --- 153.3862 183.0567 191.0051
The first line of "low frequencies" have values within ± 33 cm-1, which is rather large a range. This is due to an insufficient basis set for a rather complex molecule. The second line of "low frequencies" have only positive values, which are about one order of magnitude larger than the first line values.
Firstly, the maximum and RMS displacement values do not differ by too large a value compared to the threshold. Secondly, there are only positive vibrational frequencies, which means that the optimised structure is at ground state and the job is successful. From these, it can be concluded that the frequency job is acceptable.
Population analysis
The data from the population analysis are shown below.
| File type | .log |
| Calculation type | SP |
| Calculation method | RB3LYP |
| Basis set | 6-31G(d,p) |
| Charge | 1 |
| Spin | Singlet |
| Final energy /au | -500.8270031 |
| RMS Gradient /au | - |
| Dipole moment /D | 17.64 |
| Point group | C1 |
| Calculation time | 53.1 seconds |
Table 7. MO (6-31G;d,p) data of [P(CH3)4]+.
The final energy and dipole moment obtained are -500.8270031 au and 17.64 D respectively, which are identical to those of the optimisation and frequency jobs.
Data and Analysis of [S(CH3)3]+
Optimisation, frequency, population and NBO analysis are performed for [S(CH3)3]+ and the data then analysed.
Optimisation
The data from the optimisation calculation are shown below.
| File type | .log |
| Calculation type | FOPT |
| Calculation method | RB3LYP |
| Basis set | 6-31G(d,p) |
| Charge | 1 |
| Spin | Singlet |
| Final energy /au | -517.6832785 |
| RMS Gradient /au | 0.00001074 |
| Dipole moment /D | 10.03 |
| Point group | C1 |
| Calculation time | 4 minutes 23.0 seconds |
Table 8. Optimisation (6-31G;d,p) data of [S(CH3)3]+.
The optimisation job is complete as the RMS gradient obtained is 0.00001074, which is less than 0.001 and close to 0. The final energy obtained is -517.6832785 au.
Item Value Threshold Converged?
Maximum Force 0.000039 0.000450 YES
RMS Force 0.000009 0.000300 YES
Maximum Displacement 0.000582 0.001800 YES
RMS Displacement 0.000169 0.001200 YES
Predicted change in Energy=-1.548565D-08
Optimization completed.
-- Stationary point found.
The optimisation job is converged. The force and displacement values are within the threshold.
Frequency
The data from the frequency calculation are shown below.
| File type | .log |
| Calculation type | FREQ |
| Calculation method | RB3LYP |
| Basis set | 6-31G(d,p) |
| Charge | 1 |
| Spin | Singlet |
| Final energy /au | -517.6832785 |
| RMS Gradient /au | 0.00001070 |
| Dipole moment /D | 10.03 |
| Point group | C1 |
| Calculation time | 4 minutes 32.3 seconds |
Table 9. Frequency (6-31G;d,p) data of [S(CH3)3]+.
The frequency job is complete as the RMS gradient obtained is 0.00001070, which is less than 0.001 and close to 0; it is also very close to that obtained from the optimisation job. The final energy obtained is -517.6832785 au, which is identical to the value obtained from the optimisation job. The dipole moment of 10.03 D is also identical to that obtained from the optimisation job.
Item Value Threshold Converged? Maximum Force 0.000033 0.000450 YES RMS Force 0.000011 0.000300 YES Maximum Displacement 0.006031 0.001800 NO RMS Displacement 0.002237 0.001200 NO Predicted change in Energy=-1.770380D-07
The frequency job is not converged. The force values are within the threshold but the displacement values are not and this could be due to the presence of a very gentle potential energy surface and soft vibrational modes. Thus, it can be hard to distinguish whether the displacement values have converged. However, to further confirm the validity of this frequency job, the "low frequencies" values need to be assessed.
Low frequencies --- -13.3674 -11.3519 -0.0047 -0.0030 -0.0018 22.9063 Low frequencies --- 158.5408 194.0652 198.4901
The first line of "low frequencies" have values within ± 35 cm-1, which is rather large a range. The second line of "low frequencies" have only positive values, which are about one order of magnitude larger than the first line values, and this means that the optimised structure is at ground state and the job is successful. Moreover, the maximum and RMS displacement values do not differ by too large a value compared to the threshold. Overall, this means that the frequency job is acceptable.
Population analysis
The data from the population analysis are shown below.
| File type | .log |
| Calculation type | SP |
| Calculation method | RB3LYP |
| Basis set | 6-31G(d,p) |
| Charge | 1 |
| Spin | Singlet |
| Final energy /au | -517.6832785 |
| RMS Gradient /au | - |
| Dipole moment /D | 10.03 |
| Point group | C1 |
| Calculation time | 35.0 seconds |
Table 10. MO (6-31G;d,p) data of [S(CH3)3]+.
The final energy and dipole moment obtained are -517.6832785 au and 10.03 D respectively, which are identical to those of the optimisation and frequency jobs.
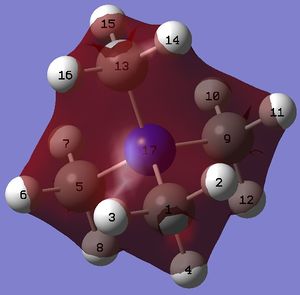
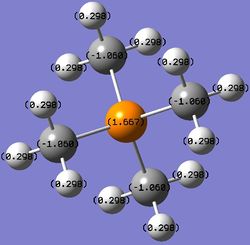
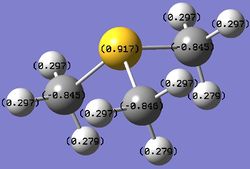
Geometries of 'onium' cations
The geometries, bond angles and bond distances, of 'onium' cations are compared and contrasted in the following section.
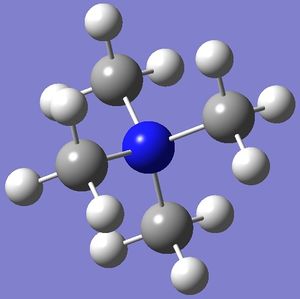
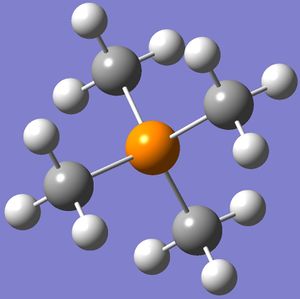
The optimised structures of 'onium' cations are shown on the right.
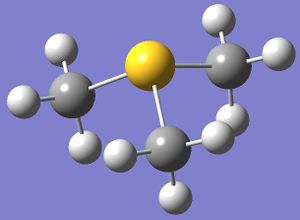
The bond angles and bond distances are listed in Tables 11 and 12 below.
| Compound | C-X-C Bond angles where X = N, P, S /° | |||||
|---|---|---|---|---|---|---|
| [N(CH3)4]+ | 109.4528 | 109.4529 | 109.4775 | 109.4813 | 109.4814 | 109.4814 |
| [P(CH3)4]+ | 109.4368 | 109.4370 | 109.4626 | 109.4666 | 109.5120 | 109.5122 |
| [S(CH3)3]+ | 102.7403 | 102.7410 | 102.7424 | |||
Table 11. Comparison of bond angles of 'onium' cations; more decimal places included to show difference in values.
From Table 11, it is clear that [N(CH3)4]+ and [P(CH3)4]+ have similar structures as they have almost identical bond angles. The almost identical C-X-C bond angles (where X = N or P) indicate that these two compounds are highly symmetrical with respect to the central heteroatom. In fact, the bond angles for these compounds are extremely close to 109.5°, which means that their structures are approximately tetrahedral.
These results are not surprising as nitrogen and phosphorus in [N(CH3)4]+ and [P(CH3)4]+ respectively both have 4 valence electrons which each participates in X-C bonding to form 4 X-C bonds. Hence, in the absence of an extra electron or a lone pair of electrons, the structures should be tetrahedral, which is confirmed by computations.
From Figure 3, [S(CH3)3]+ is seen to occupy a trigonal pyramidal structure similar to NH3. This is due to the presence of a lone pair of electron on sulfur in [S(CH3)3]+ after 3 valence electrons of sulfur each participates in S-C bonding to form 3 S-C bonds. According to VSEPR theory, lone pair-bond pair repulsion is larger than bond pair-bond pair repulsion. Hence, the C-S-C bond angle is predicted to be smaller than the ideal tetrahedral bond angle of 109.5°, which is confirmed by the computation.
| Compound | X-C bond distance where X = N, P, S /Å | Literature value for X-C bond distance /Å | ||||||
|---|---|---|---|---|---|---|---|---|
| [N(CH3)4]+ | 1.5095 | 1.5095 | 1.5095 | 1.5096 | 1.496(2) in [N(CH3)4][BrO3F2][1] |
1.490-1.501 in [N(CH3)4][(UO2)(NO3)3][2] |
1.458 in (CH3)3N[3] | |
| [P(CH3)4]+ | 1.8166 | 1.8166 | 1.8166 | 1.8169 | 1.830(5)-1.833(4) in [Co(CCH){P(CH3)3}4][4] | 1.847 in (CH3)3P[3] | ||
| [S(CH3)3]+ | 1.8226 | 1.8228 | 1.8228 | - | 1.837-1.839 (using B3LYP/6-31G(d)) in [Se(SCH3)2][5] | |||
Table 12. Comparison of bond distances of 'onium' cations; more decimal places included to show difference in values.
Nitrogen and phosphorus are in the same group in the periodic table of elements. Since nitrogen is a smaller element, it has a larger effective nuclear charge and its electrons are held closer to the nucleus and hence, a smaller electron-electron repulsion is expected between nitrogen and carbon atoms which are directly bonded. This leads to a shorter bond length. Furthermore, nitrogen, being a very electronegative element, attracts electrons to itself to a larger extent compared to phosphorus. Thus, the N-C bond is strengthened, leading to shorter bond length as well. Additionally, nitrogen and carbon are next to each other in the periodic table of elements. This means that their atomic orbitals are of similar sizes and therefore can overlap better to form molecular orbitals, leading to larger bond strength and shorter bond length.
Phosphorus and sulfur are next to each other in the periodic table of elements, having similar electronegativity and size. In other words, the bond distance of P-C and S-C should be very similar. This is indeed the case as shown in Table 12.
From Table 12, the N-C bond distances are in good agreement with literature values. The N-C bond lengths are longer than those in the neutral trimethylamine molecule because the greater steric hindrance due to an additional methyl group experienced by the small nitrogen atom lengthens the N-C bond distance to minimise steric repulsion.
The P-C bond distances are also in good agreement with literature values. They are very slightly shorter than those in [Co(CCH){P(CH3)3}4] because the much larger cobalt-containing group lengthens the P-C bond distance to minimise steric repulsion. However, the P-C bond distances are slightly shorter than those in the neutral trimethylphosphine molecule possibly because the steric effect is less significant in phosphorus, which is much bigger than nitrogen.
The S-C bond distances in [S(CH3)3]+ are quite similar to those found in [Se(SCH3)2], which is the most similar compound searched for.
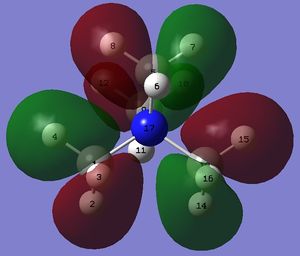
Charge distribution of 'onium' cations
The charges on each atom of the 'onium' cations are compared in the following section.
| Compound | Charge distribution without actual charges | Charge distribution with actual charges | Charge range | Charges | ||
|---|---|---|---|---|---|---|
| N/P/S | C | H | ||||
| [N(CH3)4]+ |  |
 |
-1.667 to 1.667 Green: positive Red: negative |
-0.295 | -0.483 | 0.269 |
| [P(CH3)4]+ |  |
 |
1.667 | -1.060 | 0.298 | |
| [S(CH3)3]+ |  |
 |
0.917 | -0.845, -0.845, -0.846 |
0.279 or 0.297 | |
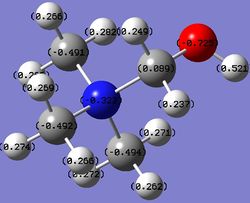
Table 13. Charges of atoms in 'onium' cations.
From Table 13, the carbon atoms in the different 'onium' cation compounds have different charges. This is because they are attached to different heteroatoms with different extent of electronegativity (electronegativity values shown in Table 14). Nitrogen is the most electronegative element out of the three, followed by sulfur and phosphorus. As a result, the carbon attached to nitrogen will have the most positive charge, followed by that attached to sulfur and phosphorus. This trend is seen in Table 13.
Due to different charges on the carbon atoms in the three compounds, the hydrogen atoms directly attached to the carbon atoms also have different charges. The hydrogen atoms attached to the carbon atoms bearing the most positive charge will have the most negative charge and vice versa.
In each case, the overall charge of the compound is +1. The carbon atoms bear a negative charge because they are adjacent to many electropositive hydrogen atoms and it is also to satisfy the overall charge of the compound.
Traditionally, nitrogen in [N(CH3)4]+ is always drawn with a formal positive charge. This formal positive charge means that nitrogen is not electron-deficient. Instead of the original 5 valence electrons that nitrogen possesses, it has only four now and each valence electron participates in C-N bonding to form 4 C-N bonds. From Table 13, it is clear that nitrogen in [N(CH3)4]+ does not possess a positive charge due to its electronegativity. Instead, the atoms bearing positive charge are the hydrogen atoms which are the most electropositive elements in the molecule.
Nature of the Carbon-Heteroatom bond
The data from the NBO analysis are shown in the table below.
| Compound | Relative contribution of atoms to C-X bond where X = N/P/S /% |
Electronegativity[6] | Electronegativity difference between atoms |
Nature of covalent bond | ||
|---|---|---|---|---|---|---|
| C | X | C | X | |||
| [N(CH3)4]+ | 33.65 | 66.35 | 2.55 | 3.04 | 0.49 | Highest ionic character |
| [P(CH3)4]+ | 59.56 or 59.57 | 40.44 or 40.43 | 2.19 | 0.36 | Some ionic character | |
| [S(CH3)3]+ | 48.67 | 51.33 | 2.58 | 0.03 | Pure covalent bond | |
Table 14. Contribution of atoms to the C-X bond where X = N/P/S.
The electronegativity of the atoms increase in the following order: P < C~S < N and the electronegativity difference increases in the following order: C-S < C-P < C-N. A more electronegative atom has a larger relative contribution to a bond because it attracts the electron pair to itself to a larger extent and this explains the trend in Table 14, where the more electronegative element in the pair is seen to have a larger relative contribution to the C-X bond. For [S(CH3)3]+, since carbon and sulfur have very similar electronegativities with sulfur being very slightly more electronegative, the sulfur atom has a very slightly higher relative contribution to the C-S bond. The larger the electronegativity difference between the atoms in a bond, the larger the relative contribution of the more electronegative atom to the C-X bond, for instance, nitrogen has the largest relative contribution of 66.35 % comparing the atoms in the three 'onium' cations.
The electronegativity difference between carbon and nitrogen is the largest and this should manifest in large positive and negative charges on carbon and nitrogen respectively due to their electronegativity values. However, this is not the case as shown in Table 13. Both carbon and nitrogen atoms possess negative charges and the negative charge on the carbon atom is larger in magnitude than that on the nitrogen atom. This is due to the following reasons. Firstly, as a result of the overall 1+ charge of [N(CH3)4]+, a valence electron on nitrogen is removed. Due to this electron deficiency, nitrogen has a smaller negative charge than expected. Secondly, nitrogen, being a very electronegative atom, does not have the positive charge localised onto itself. Instead, the 1+ charge is delocalised more throughout the whole compound and as a result, the charge of each atom becomes slightly more positive than in a neutral molecule to make up an overall charge of the compound of 1+. Thirdly, carbon and nitrogen atoms are in the same period of the periodic table of elements; thus, there is a large extent of orbital overlap between the two atoms, forming large bonding interaction between carbon and nitrogen atoms. Consequently, the electronegativity of nitrogen atom can be also spread over to the carbon atom, leading to a more negative charge for the carbon atom than expected. Lastly, since nitrogen and hydrogen atoms have 'fixed' negative and positive charges by virtue of their electronegativities being on two different ends of the electronegativity scale, the only way to make up an overall 1+ charge is to have a negative charge on each carbon atom. This is despite the fact that carbon directly attached to the electronegative atom is predicted to have a positive charge.
The electronegativity difference between carbon and phosphorus is slightly smaller. One of the valence electrons on phosphorus is removed and as the phosphorus atom is much more electropositive than the carbon atom, the 1+ charge of [P(CH3)4]+ is localised on the phosphorus atom, resulting in a large positive charge of 1.667. With a small change of charge for hydrogen atoms compared to [N(CH3)4]+, to make up an overall charge of 1+, each carbon atom has a large and negative charge. Like [N(CH3)4]+, [P(CH3)4]+ also has a relatively large electronegativity difference between the carbon and heteroatom. Therefore, both compounds have covalent C-X bonds with ionic characters.
The electronegativity difference between carbon and sulfur is very small. Therefore, the C-S bond is (almost) purely covalent with little or no ionic character. The 1+ charge is localised on the sulfur atom, contrary to the prediction on the basis of electronegativity. This is most probably due to the fact that the sulfur atom is electron deficient due to the removal of one valence electron. Given 'fixed' negative and positive charges of sulfur and hydrogen atoms, to make up an overall charge of 1+, the remaining carbon atoms each possesses a negative charge.
Data and Analysis of [N(CH3)3(CH2OH)]+
Optimisation, frequency, population and NBO analysis are performed for [N(CH3)3(CH2OH)]+ and the data then analysed.
Optimisation
The data from the optimisation calculation are shown below.
| File type | .log |
| Calculation type | FOPT |
| Calculation method | RB3LYP |
| Basis set | 6-31G(d,p) |
| Charge | 1 |
| Spin | Singlet |
| Final energy /au | -289.3947234 |
| RMS Gradient /au | 0.00001068 |
| Dipole moment /D | 2.03 |
| Point group | C1 |
| Calculation time | 31 minutes 38.7 seconds |
Table 15. Optimisation (6-31G;d,p) data of [N(CH3)3(CH2OH)]+.
The optimisation job is complete as the RMS gradient obtained is 0.00001068, which is less than 0.001 and close to 0. The final energy obtained is -289.3947234 au.
Item Value Threshold Converged?
Maximum Force 0.000035 0.000450 YES
RMS Force 0.000008 0.000300 YES
Maximum Displacement 0.001789 0.001800 YES
RMS Displacement 0.000372 0.001200 YES
Predicted change in Energy=-2.926706D-08
Optimization completed.
-- Stationary point found.
The optimisation job is converged. The force and displacement values are within the threshold.
Frequency
The data from the frequency calculation are shown below.
| File type | .log |
| Calculation type | FREQ |
| Calculation method | RB3LYP |
| Basis set | 6-31G(d,p) |
| Charge | 1 |
| Spin | Singlet |
| Final energy /au | -289.3947234 |
| RMS Gradient /au | 0.00001070 |
| Dipole moment /D | 2.03 |
| Point group | C1 |
| Calculation time | 11 minutes 45.5 seconds |
Table 16. Frequency (6-31G;d,p) data of [N(CH3)3(CH2OH)]+.
The frequency job is complete as the RMS gradient obtained is 0.00001070, which is less than 0.001 and close to 0; it is also very close to that obtained from the optimisation job. The final energy obtained is -289.3947234 au, which is identical to the value obtained from the optimisation job. The dipole moment of 2.03 D is also identical to that obtained from the optimisation job.
Item Value Threshold Converged? Maximum Force 0.000038 0.000450 YES RMS Force 0.000011 0.000300 YES Maximum Displacement 0.001402 0.001800 YES RMS Displacement 0.000404 0.001200 YES Predicted change in Energy=-2.601505D-08 Optimization completed. -- Stationary point found.
The frequency job is converged. The force and RMS displacement values are within the threshold.
Low frequencies --- -3.6883 -0.0009 -0.0004 -0.0001 8.7274 24.9377 Low frequencies --- 132.6063 216.2056 255.8028
The first line of "low frequencies" have values within 28 cm-1, which is rather large a range. The second line of "low frequencies" have only positive values, which are about one order of magnitude larger than the first line values. This means that the frequency job is complete.
Population analysis
The data from the population analysis are shown below.
| File type | .log |
| Calculation type | SP |
| Calculation method | RB3LYP |
| Basis set | 6-31G(d,p) |
| Charge | 1 |
| Spin | Singlet |
| Final energy /au | -289.3947234 |
| RMS Gradient /au | - |
| Dipole moment /D | 2.03 |
| Point group | C1 |
| Calculation time | 3 minutes 47.0 seconds |
Table 17. MO (6-31G;d,p) data of [N(CH3)3(CH2OH)]+.
The final energy obtained is -289.3947234 au, which is identical to that of the optimisation and frequency jobs. The dipole moment obtained is 2.03 D, which is identical to that of the optimisation and frequency jobs.
Data and Analysis of [N(CH3)3(CH2CN)]+
Optimisation, frequency, population and NBO analysis are performed for [N(CH3)3(CH2CN)]+and the data then analysed.
Optimisation
The data from the optimisation calculation are shown below.
| File type | .log |
| Calculation type | FOPT |
| Calculation method | RB3LYP |
| Basis set | 6-31G(d,p) |
| Charge | 1 |
| Spin | Singlet |
| Final energy /au | -306.3937693 |
| RMS Gradient /au | 0.00000757 |
| Dipole moment /D | 19.88 |
| Point group | C1 |
| Calculation time | 8 minutes 28.8 seconds |
Table 18. Optimisation (6-31G;d,p) data of [N(CH3)3(CH2CN)]+.
The optimisation job is complete as the RMS gradient obtained is 0.00000757, which is less than 0.001 and close to 0. The final energy obtained is -306.3937693 au.
Item Value Threshold Converged?
Maximum Force 0.000024 0.000450 YES
RMS Force 0.000006 0.000300 YES
Maximum Displacement 0.001337 0.001800 YES
RMS Displacement 0.000295 0.001200 YES
Predicted change in Energy=-1.416893D-08
Optimization completed.
-- Stationary point found.
The optimisation job is converged. The force and displacement values are within the threshold.
Frequency
The data from the frequency calculation are shown below.
| File type | .log |
| Calculation type | FREQ |
| Calculation method | RB3LYP |
| Basis set | 6-31G(d,p) |
| Charge | 1 |
| Spin | Singlet |
| Final energy /au | -306.3937693 |
| RMS Gradient /au | 0.00000736 |
| Dipole moment /D | 19.88 |
| Point group | C1 |
| Calculation time | 11 minutes 30.0 seconds |
Table 19. Frequency (6-31G;d,p) data of [N(CH3)3(CH2CN)]+.
The frequency job is complete as the RMS gradient obtained is 0.00000736, which is less than 0.001 and close to 0; it is also close to that obtained from the optimisation job. The final energy obtained is -306.3937693 au, which is identical to the value obtained from the optimisation job. The dipole moment of 19.88 D is also identical to that obtained from the optimisation job.
Item Value Threshold Converged? Maximum Force 0.000018 0.000450 YES RMS Force 0.000007 0.000300 YES Maximum Displacement 0.002206 0.001800 NO RMS Displacement 0.000620 0.001200 YES Predicted change in Energy=-1.227308D-08
The frequency job is converged. The force RMS and displacement values are within the threshold but the maximum displacement value is not. To further confirm the validity of this frequency job, the "low frequencies" values need to be assessed.
Low frequencies --- -12.0356 -0.0008 -0.0005 -0.0003 5.4930 13.4027 Low frequencies --- 91.4857 153.9894 210.0778
The first line of "low frequencies" have values within ± 25 cm-1. Although the range is larger than expected, it is acceptable as the method and basis set used are not sufficient and there could be soft vibrational modes. The second line of "low frequencies" have only positive values, which are about one order of magnitude larger than the first line values, and this means that the optimised structure is at ground state and the job is successful. Overall, the frequency job is acceptable.
Population analysis
The data from the population analysis are shown below.
| File type | .log |
| Calculation type | SP |
| Calculation method | RB3LYP |
| Basis set | 6-31G(d,p) |
| Charge | 1 |
| Spin | Singlet |
| Final energy /au | -306.3937693 |
| RMS Gradient /au | - |
| Dipole moment /D | 19.88 |
| Point group | C1 |
| Calculation time | 1 minute 41.9 seconds |
Table 20. MO (6-31G;d,p) data of [N(CH3)3(CH2CN)]+.
The final energy obtained is -306.3937693 au, which is identical to that of the optimisation and frequency jobs. The dipole moment obtained is 19.88 D, which is identical to that of the optimisation and frequency jobs.
Influence of functional groups on bond length
The C-N bond length of the nitrogen-containing onium cations are compared in the following section.
| [N(CH3)4]+ | [N(CH3)3(CH2OH)]+ | [N(CH3)3(CH2CN)]+ | |
|---|---|---|---|
| C-N Bond length for C atom attached to OH or CN /Å | - | 1.55 | 1.53 |
| C-N Bond length for other C atoms /Å | 1.51 | 1.50 or 1.51 | 1.51 |
Table 21. C-N bond length of 'onium' cations.
From Table 21, the C-N bond length for the carbon atoms not attached to either CN or OH is the same (a negligible difference for the C-N bond length in [N(CH3)3(CH2OH)]+. This is because the electron donating and withdrawing effect of the OH and CN group respectively does not spread through the structure to affect the other carbon atoms that are far away.
It might be expected that the C-N bond length for the carbon attached to CN is shorter than that in [N(CH3)4]+ due to the electron withdrawing effect of CN and a longer C-N bond length than that in [N(CH3)4]+ due to the electron donating effect of OH. However, this is not the trend observed. As a result, it can be concluded that the nature of substituents plays a small or minimal role in determining C-N bond length. On the other hand, the longer C-N bond lengths observed in [N(CH3)3(CH2OH)]+ and [N(CH3)3(CH2CN)]+ could be attributed to the larger size of OH and CN groups compared to the hydrogen atom if no substituents were present. The OH and CN groups are much larger and have more electrons than a hydrogen atom, and this leads to a larger electronic repulsion, lengthening the C-N bond. Since OH is a slightly larger group than CN, the C-N bond length for the carbon attached to OH in [N(CH3)3(CH2OH)]+ is longer.
Influence of functional groups on charge distribution
The charges of each atom of the nitrogen-containing compounds are compared in the following section.
| Compound | Charge distribution without actual charges | Charge distribution with actual charges | Charge range | Charges | ||||
|---|---|---|---|---|---|---|---|---|
| N | C* (adjacent to OH or CN) |
H (attached to C*) |
C (Others) | H (Others) | ||||
| [N(CH3)4]+ | |
|
-0.725 to 0.725 Green: positive Red: negative |
-0.295 | - | - | -0.483 | 0.269 |
| [N(CH3)3(CH2OH)]+ |  |
 |
-0.322 | 0.089 | 0.237 or 0.249 |
-0.491, -0.492, -0.494 |
0.262 to 0.282 | |
| [N(CH3)3(CH2CN)]+ |  |
 |
-0.289 | -0.358 | 0.309 | -0.485, -0.489, -0.489 |
0.269 to 0.282 | |
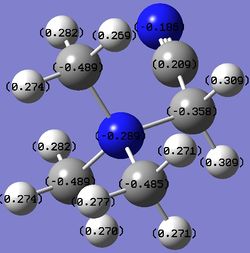
Table 22. Charges of atoms in 'onium' cations.
In [N(CH3)3(CH2OH)]+, the carbon atom adjacent to both the nitrogen atom and the OH group has a more positive charge, and it is in fact a slightly positive value, compared to the carbon atoms in the tetrahedral, symmetrical [N(CH3)4]+. This is because the carbon atom is adjacent to two very electronegative atoms, which change the charge on carbon to a large extent such that it becomes a small positive value. As OH is an electron donating group, it donates its electrons over the C-N framework and most of the electron density donated ends up on nitrogen since it is very electronegative. This is shown by a more negative charge on nitrogen compared to the nitrogen atom in [N(CH3)4]+. The hydrogen atoms attached to the carbon atom between the nitrogen atom and the OH group have charges of 0.237 or 0.249, and these are less positive than the charges of hydrogen atoms in [N(CH3)4]+ because OH donates electron density through the C-N framework and this reduces the charge on the hydrogen atoms as well.
In [N(CH3)3(CH2CN)]+, the carbon atom between the nitrogen atom and the CN group has a negative charge but it has a smaller magnitude compared to the carbon atoms in the tetrahedral, symmetrical [N(CH3)4]+. This is because the electron-withdrawing effect of the CN group withdraws electron through the C-N framework, resulting in a smaller electron density and a less negative charge on the central nitrogen atom. The carbon atom directly attached to the central nitrogen atom also has its electron density withdrawn towards the CN group, leading to a less negative charge. The hydrogen atoms attached to this carbon atom have charges of 0.309, and it is more positive than the hydrogen atoms in [N(CH3)4]+ because CN withdraws electron density through the C-N framework and this increases the charge on the hydrogen atoms as well.
In each case, the overall charge of the compound is +1. The other carbon and hydrogen atoms are far away from either the OH or CN group to be able to experience a large change in charge. Therefore, their charges are similar to the carbon atoms in the tetrahedral, symmetrical [N(CH3)4]+.
Comparison of HOMO and LUMO
The HOMO and LUMO of [N(CH3)4]+, [N(CH3)3(CH2OH)]+ and [N(CH3)3(CH2CN)]+ are compared in the following section.
| Compound | HOMO | Energy /au |
LUMO | Energy /au |
HOMO-LUMO gap /au |
|---|---|---|---|---|---|
| [N(CH3)4]+ |  |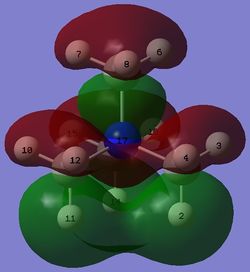
-0.57929 |  |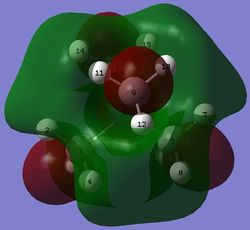
-0.13305 | 0.44624 |
| [N(CH3)3(CH2OH)]+ |  |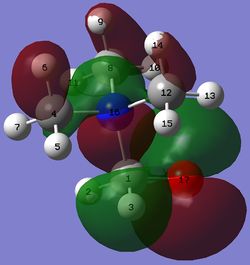
-0.48759 |  |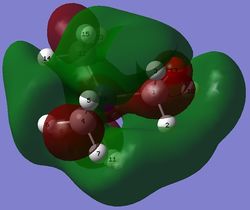
-0.12463 | 0.37296 |
| [N(CH3)3(CH2CN)]+ |  |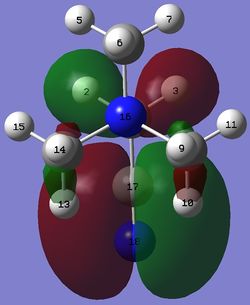
-0.50048 |  |
-0.18183 | 0.31865 |
Table 23. HOMO and LUMO of 'onium' cations.
Shape of the HOMOs
The HOMO of the compounds changes to a large extent.
In the HOMO of [N(CH3)4]+, all atoms participate in either bonding or anti-bonding interaction. However, this is not the case in the HOMO of [N(CH3)3(CH2OH)]+ where atoms, such as H5, H7, C12 and others, do not participate in any form of interactions. As a result of the electronegative oxygen of the OH group, there is a large amount of electron density localised on the OH group. Moreover, as the OH group donates electrons onto neighbouring atoms, a large increase in electron density on the neighbouring carbon and hydrogen atoms is observed, as seen in large lobes of electron density on these atoms. However, the addition of the OH group has also led to the loss of many strong through bond and through space bonding interactions between atoms, such as the green structure between H2, H11 and H14 and red structure between H6, H7 and H8 in [N(CH3)3(CH2OH)]+ as compared to [N(CH3)4]+. This might be because the oxygen atom is very electronegative and withdraws electron density throughout the entire carbon framework despite the fact that the OH group is electron donating.
In the HOMO of [N(CH3)3(CH2CN)]+, the addition of the electron withdrawing CN group has led to the loss of an even larger amount of electron density on many atoms in [N(CH3)3(CH2CN)]+. For instance, there is only some electron density on the -CH2 group adjacent to the CN group and a very small amount of electron density on two of the three methyl groups. It is interesting to note the huge effect of the electron withdrawing CN. As a result, most of the electron density is localised on the bonding orbital of the CN group with huge lobes on each of the carbon and nitrogen atoms.
Shape of the LUMOs
The LUMO of the compounds remains roughly similar.
In the LUMO of [N(CH3)4]+, there is a large anti-bonding interaction between the s AO of nitrogen and p AO of carbon atoms, resulting in a red structure for nitrogen embedded in the MO. The large delocalised green structure throughout the MO can be explained by the large and strong through-space bonding interaction between the p AO of carbon atoms. Hydrogen atoms do not participate in either bonding or anti-bonding interactions in this MO.
In the LUMO of [N(CH3)3(CH2OH)]+, the s AO of the nitrogen atom forms a bonding interaction with the p AO of the carbon in the -CH2OH group and this p AO of carbon then forms a bonding interaction with the p AO of the oxygen atom. As a result, there is a red bonding structure across the nitrogen, carbon and oxygen atoms. The three other methyl groups look very similar to the LUMO of [N(CH3)4]+. The bonding interactions in this MO are slightly enhanced due to the electron donating nature of the OH group.
In the LUMO of [N(CH3)3(CH2CN)]+, there is a large anti-bonding interaction between carbon and nitrogen in the CN group and there is a node between these atoms. Due to the electron withdrawing nature of the CN group, it withdraws electron density from the carbon framework and consequently, there is minimal electron density on each hydrogen atom. The three other methyl groups look very similar to the LUMO of [N(CH3)4]+. The anti-bonding interactions in this MO are enhanced due to the electron withdrawing nature of the CN group.
However, as the LUMO is not occupied by electrons, it can be hard to determine the actual structure of the LUMO. The computations performed are usually just guesses of the structure of the LUMO.
Energy level of the HOMO and LUMO
The energies of the HOMO and LUMO of [N(CH3)3(CH2OH)]+ and [N(CH3)3(CH2CN)]+ have changed with respect to [N(CH3)4]+. However, the energy levels of the HOMO and LUMO cannot be compared in this way as the orbitals involved in each case looks quite different, and this is especially so for the HOMOs. In fact, the HOMOs of [N(CH3)3(CH2OH)]+ and [N(CH3)3(CH2CN)]+ have raised energies as there are smaller bonding interactions and increased anti-bonding interactions compared to [N(CH3)4]+.
To do a proper comparison of the orbitals, there is a need to look at MOs of [N(CH3)3(CH2OH)]+ and [N(CH3)3(CH2CN)]+ that resemble the HOMO and LUMO of [N(CH3)4]+. This will be done in the next section.
The energy of the HOMO of [N(CH3)3(CH2OH)]+ and [N(CH3)3(CH2CN)]+ has increased, whereas the energy of the LUMO of [N(CH3)3(CH2OH)]+ and [N(CH3)3(CH2CN)]+ has increased and decreased respectively. The increase in energy of the HOMO means that the HOMO of these compounds is now closer in energy to the LUMO of compounds that they might interact in. In other words, assuming that they interact with the same compound X with a LUMO at energy level -0.2, they will both form larger interaction and interact at a higher rate compared to [N(CH3)4]+ since the HOMO-LUMO gap between the reagents is now smaller. On the other hand, a LUMO lower in energy means that the compound will be closer to HOMO of the compound it reacts with, hence leading to larger interaction and more facile interaction due to the proximity of the HOMO and LUMO.
As [N(CH3)3(CH2CN)]+ has a raised HOMO energy and lowered LUMO energy, resulting in a smaller HOMO-LUMO gap, it will be more reactive than [N(CH3)4]+. Similarly, [N(CH3)3(CH2OH)]+ is also expected to be more reactive than [N(CH3)4]+ as the former has a greatly increased HOMO energy and a slightly decreased LUMO energy, also resulting in a smaller HOMO-LUMO gap. [N(CH3)3(CH2OH)]+ and [N(CH3)3(CH2CN)]+ with smaller HOMO-LUMO gaps are 'softer' than [N(CH3)4]+. This means that if they act as nucleophiles or bases, they are more likely to donate electrons to electrophiles or acids and they do so more readily.[7]
MOs that resemble the HOMO of [N(CH3)4]+
The MOs from [N(CH3)3(CH2OH)]+ and [N(CH3)3(CH2CN)]+ that resemble the HOMO of [N(CH3)4]+ are shown below.
| [N(CH3)4]+ | [N(CH3)3(CH2OH)]+ | [N(CH3)3(CH2CN)]+ | ||
|---|---|---|---|---|
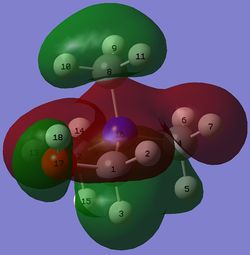
| MO | |
 |
 |
|
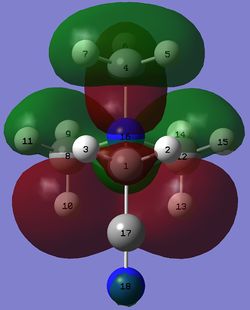
| Level of MO | 21 | 15 | 15 | 23 |
| Energy of MO /au | -0.57929 | -0.69723 | -0.72365 | -0.59176 |
Table 24. MOs that resemble the HOMO of [N(CH3)4]+.
The three MOs that resemble the HOMO of [N(CH3)4]+ have a larger degree of bonding interaction and a smaller degree of anti-bonding interaction. As a result, they all have lower energy than the HOMO of [N(CH3)4]+.
The 15th MO of [N(CH3)3(CH2OH)]+ has all atoms participating in bonding or anti-bonding interactions. It is interesting to note that H11 and H15 of the 15th MO of [N(CH3)3(CH2CN)]+ and a large part of the CH2CN fragment of the 23rd MO of [N(CH3)3(CH2CN)]+ do not participate in any bonding or anti-bonding interaction.
Conclusion
The computations were all complete with the data and analysis presented above. Where a comparison with literature values was made, the values obtained from the computations mostly agree with the literature values. Computational methods have proved useful to ascertain the structure of the MOs, the nature of bonding within compounds and the charge distribution of atoms in compounds. The properties of selected 'onium' cations were compared and contrasted, and the effects of functional groups explained. To improve the experiment, a larger set of compounds could be included and their vibrational frequency data analysed to confirm the trends observed.
References
- ↑ J. F. Lehmann, G. J. Schrobilgen, "Synthesis and characterization of salts containing the BrO(3)F(2)(-) anion; a rare example of a bromine(VII) species", J. Am. Chem. Soc., 2005, 127, 9416–27. DOI:10.1021/ja0402607
- ↑ K. M. Ok, M. B. Doran, D. O’Hare , "[N(CH3)4][(UO2)2F5]: A new organically templated open-framework uranium oxide fluoride (MUF-2) (Electronic Supplementary Information)", J. Mater. Chem., 2006, 16, 3366–3368. DOI:10.1039/b609525a
- ↑ 3.0 3.1 D. R. Lide, "Section 9: Molecular Structure and Spectroscopy", CRC Handbook of Chemistry and Physics, CRC Press, 2005, 41.
- ↑ G. Stringer, N. J. Taylor, T. B. Marder, "Ethynyltetrakis(trimethylphosphine)cobalt(I), [Co(CCH){P(CH3)3}4]", Acta Crystallogr., Sect. C: Cryst. Struct. Commun., 1996, 52, 80-82. DOI:10.1107/S0108270195010304
- ↑ H. Fleischer, D. A. Wann, S. L. Hinchley, K. B. Borisenko, J. R. Lewis, R. J. Mawhorter, E. Robertson , D. W. H. Rankin, "Molecular structures of Se(SCH3 )2 and Te(SCH3) 2 using gas-phase electron diffraction and ab initio and DFT geometry optimisations", Dalton Trans., 2005, 3221–3228. DOI:doi:10.1039/B505287B
- ↑ P. W. Atkins, T. L. Overton, J. P. Rourke, M. T. Weller, F. A. Armstrong, "Chapter 1: Atomic Structure", Shriver & Atkins' Inorganic Chemistry, 5th edition, Oxford University Press, 2010, 30.
- ↑ F. A. Carey, R. J. Sundberg, "Chapter 1: Chemical Bonding and Structure", Advanced Organic Chemistry: Part A: Structure and Mechanisms (4th edition), Kluwer Academic/Plenum Publishers, 2000, 21.