Rep:Mod:knt11backup

Third year Inorganic Computational Laboratory

Name: Kai Ni Teh
CID: 00697229

CITE!!!
label tables + caption
Be sure to summarize the details of the calculation, such as basis set and method, also show on your wiki that the optimisation is converged, that the low frequencies are low and that there are no negative frequencies.
comment that same basis set to be used; meaningless to compare energies..
IR rocking?

Optimisation Analysis

Data

The relevant optimisation data for BH₃, GaBr₃ and BBr₃ are shown in Table 1.


	BH₃ (3-21G)	BH₃ (6-31G;d,p)	GaBr₃ (LanL2DZ)	BBr₃ (Gen)
File	KNT BH₃ optimisation (3-21G)	KNT BH₃ optimisation (6-31G;d,p)	KNT GaBr₃ optimisation (LanL2DZ)	KNT BBr₃ optimisation (Gen)
File type	.log	.log	.log	.log
Calculation type	FOPT	FOPT	FOPT	FOPT
Calculation method	RB3LYP	RB3LYP	RB3LYP	RB3LYP
Basis set	3-21G	6-31G(d,p)	LanL2DZ	Gen
Charge	0	0	0	0
Spin	Singlet	Singlet	Singlet	Singlet
Final energy /au	-26.4622634	-26.6153236	-41.7008278	-64.4364530
RMS Gradient /au	0.00020672	0.00000235	0.00000016	0.00000382
Dipole moment /D	0.00	0.00	0.00	0.00
Point group	D_3h	D_3h	D_3h	D_3h
Calculation time	1 minute 0.0 seconds	44.0 seconds	27.7 seconds	36.9 seconds
Bond distance /Å	1.19	1.19	2.35	1.93
Bond angle /°	120.0	120.0	120.0	120.0
Total energy /au	-26.4622634	-26.6153236	-41.7008278	-64.4364530

Table 1. Optimisation data for various compounds.

BH₃ optimisation (3-21G)

 Item                     Value        Threshold    Converged?
 Maximum Force            0.000413     0.000450     YES
 RMS     Force            0.000271     0.000300     YES
 Maximum Displacement     0.001610     0.001800     YES
 RMS     Displacement     0.001054     0.001200     YES
 Predicted change in Energy=-1.071764D-06
 Optimization completed.
    -- Stationary point found.

BH₃ optimisation (6-31G;d,p)

 Item                     Value        Threshold    Converged?
 Maximum Force            0.000005     0.000450     YES
 RMS     Force            0.000003     0.000300     YES
 Maximum Displacement     0.000019     0.001800     YES
 RMS     Displacement     0.000012     0.001200     YES
 Predicted change in Energy=-1.305135D-10
 Optimization completed.
    -- Stationary point found.

GaBr₃ optimisation (LanL2DZ)

 Item                     Value        Threshold    Converged?
 Maximum Force            0.000000     0.000450     YES
 RMS     Force            0.000000     0.000300     YES
 Maximum Displacement     0.000003     0.001800     YES
 RMS     Displacement     0.000002     0.001200     YES
 Predicted change in Energy=-1.282681D-12
 Optimization completed.
    -- Stationary point found.

BBr₃ optimisation (Gen)

 Item                     Value        Threshold    Converged?
 Maximum Force            0.000008     0.000450     YES
 RMS     Force            0.000005     0.000300     YES
 Maximum Displacement     0.000036     0.001800     YES
 RMS     Displacement     0.000023     0.001200     YES
 Predicted change in Energy=-4.026916D-10
 Optimization completed.
    -- Stationary point found.

For each compound, the optimisation is shown to converge. The force and displacement values were within the threshold. The bond lengths and bond angles are also shown.

The optimisations are accurate as the correct point group and bond angle are shown for each molecule.

Analysis: Comparison of bond distances


Compounds	Computed bond distances /Å	Literature values for bond distances /Å
Compounds	DFT/6-31G(d;p)	HF/6-31G	DFT/NLSD
BH₃	1.19	1.190 01 (1) from the ground state rotational constant B₀
BBr₃	1.93	1.893 - 1.916 BP86 PBE0 MP2 CCSD(T)
GaBr₃	2.35	2.277 (CASSCF) / 2.265 (MRSDCI + Q)

Table 2. Bond distances for various compounds.

What difference does changing the ligand have?
How are H and Br similar, how are they different?
What difference does changing the central element make?
How are B and Ga similar, how are they different?

Bond distance is dependent on bond strength which is in turn dependent on size of atoms, extent of orbital overlap between atoms, electronegativity and polarity difference between atoms.

From Table 2, as the size of the ligand increased, the bond distance increased. This is due to a large extent of increase in electron-electron repulsion when hydrogen was replaced by bromine as bromine has a much larger number of electrons as compared to hydrogen, which only has one. Also, boron is electropositive whereas hydrogen is electronegative; this leads to a strong attraction between the two atoms, resulting in a stronger and shorter bond. Hydrogen and bromine atoms are similar in that they are both atoms which contribute electrons based on their valence shell electron count; however, the large increase in number of electrons produced a large effect, hence leading to the large increase in B-H bond distance.

As the central element was changed from boron to gallium, an expected increase in bond distance was observed. This is due to the above mentioned reason where a larger atom has a larger number of electrons, and hence a larger electronic repulsion and bond distance. Gallium is the element below boron and hence is less electropositive than boron due to its larger size and more diffuse nuclear charge. This means a smaller force of attraction between gallium and bromine, and hence a longer bond. Also, gallium and bromine atoms are larger than boron and hydrogen respectively; this means that their orbitals are more diffuse and the Ga-Br orbital overlap will be poorer. This leads to a weaker bond strength and longer bond. Even though boron and gallium are in the same group in the periodic table of elements and they both have 3 valence electrons each to bond with 3 one-electron donor ligands, it was the increase in number of electrons of the central element that led to the increase in bond distance.

A comparison of the computed and literature values for the various bond distances revealed an agreement between the values and the accuracy of the computation. However, as the method and basis set used were different for this and others' computations, no more attempt at comparison could and should be made, apart from noting that they are sufficiently similar.

In some structures gaussview does not draw in the bonds where we expect, does this mean there is no bond? Why?
What is a bond?

A bond is an interaction formed between two atoms which hold them together in place. Depending on the nature of the atoms, there can be various types of bond, for instance, ionic bond, covalent bond, metallic bond and agostic bonding. The strength of a bond is usually dependent on the extent or strength of electrostatic force of attraction between the two atoms. For example, a pure ionic bond is strong as the ions are oppositely charged, leading to a large electrostatic force of attraction.

In the computational software used, Gaussview, some bonds are not drawn where we expect. However, this does not mean that there is no bond. Instead, the bond distance exceeds a pre-defined value and therefore, it cannot be shown or drawn in Gaussview.

Frequency Data and Analysis

The frequency data and analysis of BH₃ and GaBr₃ are presented in the following sections.

BH₃ frequency (6-31G;d,p)

Data


	BH₃ (6-31G;d,p)
File	KNT BH₃ frequency (6-31G;d,p)
File type	.log
Calculation type	FREQ
Calculation method	RB3LYP
Basis set	6-31G(d,p)
Charge	0
Spin	Singlet
Final energy /au	-26.6153236
RMS Gradient /au	0.00000237
Dipole moment /D	0.00
Point group	D_3h
Calculation time	13.0 seconds
Bond distance /Å	1.19
Bond angle /°	120.0
Total energy /au	-26.6153236

Table 3. Optimisation (6-31G;d,p) data for BH₃

 Item                     Value        Threshold    Converged?
 Maximum Force            0.000005     0.000450     YES
 RMS     Force            0.000002     0.000300     YES
 Maximum Displacement     0.000019     0.001800     YES
 RMS     Displacement     0.000009     0.001200     YES
 Predicted change in Energy=-1.323376D-10
 Optimization completed.
    -- Stationary point found.

The computation is shown to converge with force and displacement values within the threshold.

3N-6 vibrational frequencies

Low frequencies ---   -0.9033   -0.7343   -0.0055    6.7375   12.2491   12.2824
Low frequencies --- 1163.0003 1213.1853 1213.1880

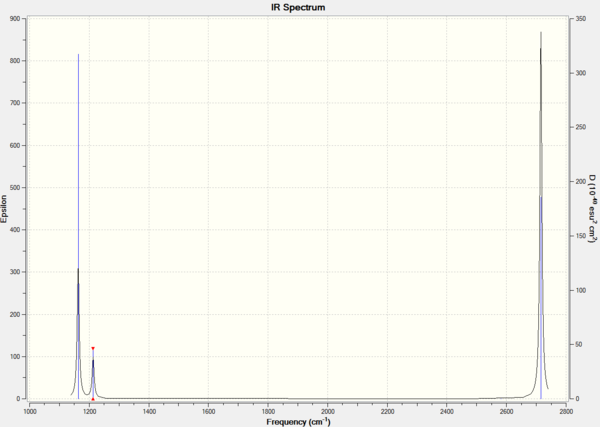
Every molecule has 3N-6 modes of vibration where N is the number of atoms in the molecule. For BH₃, there are 6 modes of vibration as N is 4. The first line of "low frequencies" shows the 6 frequencies that are removed from the 3N-6 operation. They correspond to the motion of the center of the mass of the molecule and the values should be much smaller than the second line of "low frequencies". The second line shows only three of the six remaining vibrational frequencies. Out of the 6 vibrational modes, only 3 produce a change in dipole moment upon vibration and this is reflected in the IR spectrum, which will be explained later.

The first line of "low frequencies" are low and close to zero and the second line of "low frequencies" are positive. There are also no negative frequencies. It is usually acceptable for the first line of "low frequencies" to have a range within 15 cm^-1 and the second line of "low frequencies" to differ from the first by about an order of magnitude. The frequency data fits the requirement and is hence a good computation.

In this case, the lowest normal mode of vibration is at 1163 cm^-1.

IR vibrational frequencies

Figure 1. IR spectrum of BH₃.


No.	Form of the vibration	Frequency /cm^-1	Intensity	Symmetry (D_3h point group)
1	The H atoms move up and down in a concerted fashion, whereas the B atom is stationary.	1163	93	A₂"
2	2 H atoms movie in a scissoring fashion, whereas the last H atom and B atom are stationary.	1213	14	E'
3	2 H atoms move outwarsd in a scissoring fashion, and the last H atom moves perpendicularly to the axis it is lying along.The B atom is stationary.	1213	14	E'
4	All 3 H atoms stretch symmetrically by moving outwards along their respective axis.	2582	0	A₁'
5	Two H atoms stretch asymmetrically, whereas the last H atom and B atom are stationary.	2715	126	E'
6	2 H atoms, stretching symmetrically outwards, are moving asymmetrically with respect to the remaining H atom; the B atom is stationary.	2715	126	E'

Table 4. IR data for BH₃.

explain why are there less than six peaks in the spectrum, when there are obviously six vibrations.
Six vibrational frequencies are computed, meaning that six peaks should be observed in the IR spectrum. However, only 3 peaks are observed in Figure 1. This is because the symmetric stretch at 2582 cm^-1 leads to no change in dipole moment upon vibration; hence, this peak is not IR active and has an intensity of 0. Furthermore, vibrational modes 2 and 3 at 1213 cm^-1 and 5 and 6 at 2715 cm^-1 are degenerate and produce peaks at the same frequency; therefore, for each of 2 and 3, and 5 and 6 degenerate vibrational modes, only one peak is observed.

GaBr₃ frequency (LanL2DZ)

Data


	GaBr₃ (LanL2DZ)
File	KNT GaBr₃ frequency (LanL2DZ)
File type	.log
Calculation type	FREQ
Calculation method	RB3LYP
Basis set	LanL2DZ
Charge	0
Spin	Singlet
Final energy /au	-41.7008278
RMS Gradient /au	0.00000011
Dipole moment /D	0.00
Point group	D_3h
Calculation time	16.4 seconds
Bond distance /Å	2.35
Bond angle /°	120.0
Total energy /au	-41.7008278

Table 5. Frequency (LanL2DZ) data for GaBr₃.

 Item               Value     Threshold  Converged?
 Maximum Force            0.000000     0.000450     YES
 RMS     Force            0.000000     0.000300     YES
 Maximum Displacement     0.000002     0.001800     YES
 RMS     Displacement     0.000001     0.001200     YES
 Predicted change in Energy=-6.142862D-13
 Optimization completed.
    -- Stationary point found.

The computation is shown to converge with force and displacement values within the threshold.

3N-6 vibrational frequencies

Low frequencies ---   -0.5252   -0.5247   -0.0024   -0.0010    0.0235    1.2010
Low frequencies ---   76.3744   76.3753   99.6982

The GaBr₃ frequency data prove that this computation is good as the "low frequencies" data are acceptable. This means that the frequencies are low and close to zero, the second line of frequencies has positive values, and there are no negative frequencies.

In this case, the lowest normal mode of vibration is at 76 cm^-1.

IR vibrational frequencies

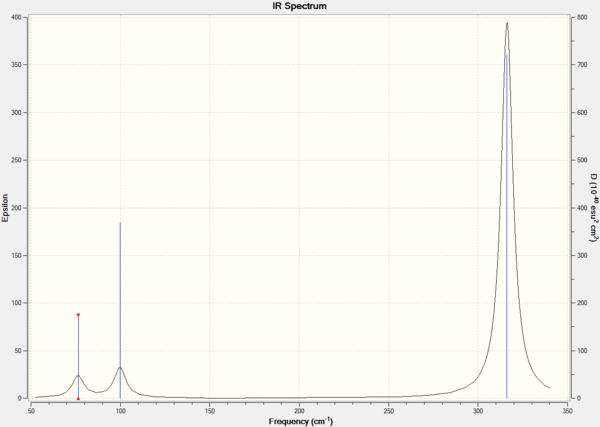
Figure 2. IR spectrum of GaBr₃.


No.	Form of the vibration	Frequency /cm^-1	Intensity	Symmetry (D_3h point group)
1	2 Br atoms move in a scissoring fashion; the remaining Br and Ga atoms also move.	76	3	E'
2	2 Br atoms move in a scissoring fashion, whereas the remaining Br and Ga atoms move outwards, opposite to that of the 2 Br atoms.	76	3	E'
3	The Ga atom moves up and down, and the Br atoms move along with the motion of the Ga atom.	100	9	A₂"
4	The Br atoms stretch outwards symmetrically, whereas the Ga atom is stationary.	197	0	A₁'
5	Two Br atoms stretch asymmetrically and the Ga atom moves downwards. The last Br atom is stationary.	316	57	E'
6	One of the Br atoms and the Ga atom move towards each other, stretching the remaining Ga_br bonds.	316	57	E'

Table 6. IR data for GaBr₃.

explain.
Only 3 peaks are observed as vibrational mode 4 is a symmetric stretch, which is IR-inactive. Vibrational modes 1 and 2, and 5 and 6 produce peaks are degenerate and hence, produce one peak for each group.

Analysis of Vibrational Frequencies

The vibrational frequencies of BH₃ and GaBr₃ are analysed and compared in the following section.


Compounds	Vibrational frequencies /cm^-1 (Symmetry label)
BH₃	1163 (A2")	1213 (E')	2582 (A1')	2715 (E')
GaBr₃	76 (E')	100 (A2")	197 (A1')	316 (E')

Table 7. Comparison of vibrational frequencies.

Why must you use the same method and basis set for both the optimisation and frequency analysis calculations?
What is the purpose of carrying out a frequency analysis?
What do the "Low frequencies" represent?

A frequency analysis is the second derivative of the potential energy surface and the sign of frequencies obtained shows the nature of the optimised structure, whether it is at ground state, a transition state or it shows the fact that the optimisation is unsuccessful. If the frequencies obtained are positive, the structure is at ground state. If one negative frequency is obtained, the structure is a transition state. If there is more than one negative frequency, the optimisation has failed. In all cases in this experiment, the frequencies obtained are all positive, indicating that the optimisations were successful as all optimised structures were at ground state, and hence most stable.

The same method and basis set for both optimisation and frequency analysis calculations have to be used as each method and basis set will lead to a different result. For instance, when a more complicated basis set for optimisation is used, the final energy of the molecule is obtained and more accurate; however, if the basis set is then changed to a simpler one for frequency analysis calculation, the energy obtained will be different from that of the optimisation. This means that the calculations are on slightly different molecules, and the difference could be in final energy, bond angle or bond distance to name a few.

What difference does changing the ligand have?
What does the large difference in the value of the frequencies for BH3 compared to GaBr3 indicate?
Has there been a reordering of modes?
How are these spectra similar?
For both spectra two modes lie fairly closely together, the A2 and E' modes and then the other two modes also lie fairly close together, the A1' and E' modes, but higher in energy. Why is this?

Vibrational frequencies are proportional to force constant and inversely proportional to the reduced mass of the molecule. The Ga-Br bond is weaker than the B-H bond as the former consists of larger atoms with more diffuse orbitals, leading to poorer overlap and weaker bond. Furthermore, Ga and Br atoms are certainly heavier than B and H atoms, leading to a larger reduced mass. As a result, BH₃ will produce vibrations at larger frequencies compared to GaBr₃. This is also shown in the computation summarised in Table 7.

Molecular Orbitals (MOs) of BH₃

The data for MO computation of BH₃ is shown below.


File	KNT BH₃ MOs
File type	.log
Calculation type	SP
Calculation method	RB3LYP
Basis set	6-31G(d,p)
Charge	0
Spin	Singlet
Final energy /au	-26.6153236
RMS Gradient /au	-
Dipole moment /D	0.00
Point group	D_3h
Calculation time	3.0 seconds

Table 8. MO data for BH₃.

MO diagram

The MO diagram of BH₃ is shown below.

Figure 3. MO diagram of BH₃
in chemdraw create your own MO diagram of trigonal planar D3h BH3 make sure to draw the LCAOs for each energy level.
using the screen capture application of your laptop take snap-shots of the occupied and LUMO orbitals that feature in your MO diagram.
place the snapshots of the "real" MOs next to the "LCAO" MOs on your diagram

Are there any significant differences between the real and LCAO MOs?
What does this say about the accuracy and usefulness of qualitative MO theory?

There are no significant differences between the real and LCAO MOs as they look highly similar in terms of shape and size. While this is especially true for the first 6 real MOs, the 7th and 8th real MOs look a little different from the predicted ones. This might be due to the limitation of LCAO ...

Overall, this means that the qualitative MO theory is sufficiently useful and accurate in this instance. However, it is only useful for prediction of interaction between atoms, and subsequently MOs, of small molecules. As the molecule gets larger, coupled with various effects such as mixing, computational methods will be required to predict the form of interaction between atoms and the real MOs.

NBO analysis of NH₃

The optimisation, frequency and charge distribution data are shown in the following section.

NH₃ optimisation (6-31G;d,p)

Data


File	KNT NH₃ optimisation (6-31G;d,p)
File type	.log
Calculation type	FOPT
Calculation method	RB3LYP
Basis set	6-31G(d,p)
Charge	0
Spin	Singlet
Final energy /au	-56.5577686
RMS Gradient /au	0.00000289
Dipole moment /D	1.85
Point group	C_3v
Calculation time	9.0 seconds
Bond distance /Å	1.02
Bond angle /°	105.7
Total energy /au	-56.5577686

Table 9. Optimisation data of NH₃.

 Item               Value     Threshold  Converged?
 Maximum Force            0.000005     0.000450     YES
 RMS     Force            0.000003     0.000300     YES
 Maximum Displacement     0.000010     0.001800     YES
 RMS     Displacement     0.000007     0.001200     YES
 Predicted change in Energy=-7.830081D-11
 Optimization completed.
    -- Stationary point found.

For NH₃, the optimisation is shown to converge. The force and displacement values were within the threshold.

NH₃ frequency

Data


File	KNT NH₃ frequency (6-31G;d,p)
File type	.log
Calculation type	FREQ
Calculation method	RB3LYP
Basis set	6-31G(d,p)
Charge	0
Spin	Singlet
Final energy /au	-56.5577686
RMS Gradient /au	0.00000281
Dipole moment /D	1.85
Point group	C_3v
Calculation time	4.0 seconds
Bond distance /Å	1.02
Bond angle /°	105.7
Total energy /au	-56.5577686

Table 10. Frequency data of NH₃.

 Item               Value     Threshold  Converged?
 Maximum Force            0.000005     0.000450     YES
 RMS     Force            0.000003     0.000300     YES
 Maximum Displacement     0.000011     0.001800     YES
 RMS     Displacement     0.000006     0.001200     YES
 Predicted change in Energy=-8.407566D-11
 Optimization completed.
    -- Stationary point found.

The computation is shown to converge with force and displacement values within the threshold.

3N-6 vibrational frequencies

Low frequencies ---  -11.6223  -11.5869   -0.0032    0.0244    0.1403   25.5604
Low frequencies --- 1089.6629 1694.1734 1694.1737

The first line of "low frequencies" shows that the vibrational frequencies differed with a range larger than ± 15 cm^-1, and this means that the computational method and basis set used were insufficient. If an improved method was used, for example as suggested by the demonstrator to include "int=ultrafine scf=conver=9" as additional keywords and to tick the option "use tight convergence criteria", the first line of "low frequencies" should vary within the acceptable range of 15 cm^-1. However, there was no need to re-perform the calculation as the demonstrator said so.

However, the second line of frequencies has positive values, and there are no negative frequencies.

MO data of NH₃

Data


File	KNT BH₃ MOs
File type	.log
Calculation type	SP
Calculation method	RB3LYP
Basis set	6-31G(d,p)
Charge	0
Spin	Singlet
Final energy /au	-56.5577686
RMS Gradient /au	-
Dipole moment /D	1.85
Point group	C_3v
Calculation time	3.0 seconds

Table 11. MO data of NH₃.

NH₃ Charge Distribution

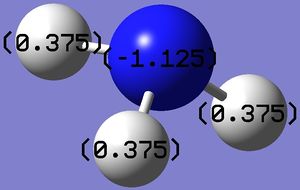
Figure 4: Charge range: -1.000 to 1.000; Figure 5: Charge on Nitrogen: -1.125, Charge on (each) Hydrogen: 0.375

Figure 4 shows the charge on each atom by showing either red or green colour for each atom. While red indicates a negative charge, green indicates a positive charge. Figure 5 shows the exact charge on each atom. The computation is good as it is commonly known that nitrogen, being an electronegative atom, possesses a negative charge. As the hydrogen atoms are directly attached to nitrogen, they are in turn electropositive and hence each possesses a positive charge.

Additionally, it is known that the total charge of a neutral compound is zero. The computation shows this as a value of zero is obtained after adding up charges on each atom.

Analysis of NH₃BH₃

NH₃BH₃ was included in this exercise to determine the reaction energy for a reaction between NH₃ and BH₃.

NH₃BH₃ optimisation (6-31G;d,p)

Data


File	KNT NH₃BH₃ optimisation (6-31G;d,p)
File type	.log
Calculation type	FOPT
Calculation method	RB3LYP
Basis set	6-31G(d,p)
Charge	0
Spin	Singlet
Final energy /au	-83.2246901
RMS Gradient /au	0.00006839
Dipole moment /D	5.57
Point group	C₁
Calculation time	24.0 seconds
B-N bond distance /Å	1.67
N-H bond distance /Å	1.02
B-H bond distance /Å	1.21
H-N-B bond angle /°	111.0
H-B-N bond angle /°	104.6
H-N-H bond angle /°	107.9
H-B-H bond angle /°	113.9
Total energy /au	-83.2246901

Table 12. Optimisation data of NH₃BH₃.

 Item                     Value        Threshold    Converged?
 Maximum Force            0.000139     0.000450     YES
 RMS     Force            0.000063     0.000300     YES
 Maximum Displacement     0.000771     0.001800     YES
 RMS     Displacement     0.000338     0.001200     YES
 Predicted change in Energy=-2.028054D-07
 Optimization completed.
    -- Stationary point found.

The optimisation is shown to converge with force and displacement values within the threshold.

A C₁ point group is revealed through the computation.

NH₃BH₃ frequency

Data


File	KNT NH₃BH₃ frequency (6-31G;d,p)
File type	.log
Calculation type	FREQ
Calculation method	RB3LYP
Basis set	6-31G(d,p)
Charge	0
Spin	Singlet
Final energy /au	-83.2246900
RMS Gradient /au	0.00006831
Dipole moment /D	5.57
Point group	C₁
Calculation time	14.0 seconds

Table 13. Frequency data of NH₃BH₃.

 Item                     Value        Threshold    Converged?
 Maximum Force            0.000127     0.000450     YES
 RMS     Force            0.000068     0.000300     YES
 Maximum Displacement     0.000828     0.001800     YES
 RMS     Displacement     0.000544     0.001200     YES
 Predicted change in Energy=-2.130705D-07
 Optimization completed.
    -- Stationary point found.

The computation is shown to converge with force and displacement values within the threshold. The final energy from the frequency computation is highly similar to the optimisation data for NH₃BH₃.

3N-6 vibrational frequencies

Low frequencies ---   -0.0007   -0.0007   -0.0006   19.0166   23.6650   42.9730
Low frequencies ---  266.5856  632.3785  639.4477

The first line of "low frequencies" again varies with a larger than expected range. To improve the result, a better method and basis should be used as outlined above.

Association and dissociation energies of NH₃BH₃

The association energy is the energy released when a bond between NH₃ and BH₃ is formed to obtain NH₃BH₃. It is determined by manipulating the final energies of NH₃BH₃, NH₃ and BH₃ as shown below. The dissociation energy is the opposite of association energy when the B-N bond in NH₃BH₃ breaks to give NH₃ and BH₃.

Association energy

E(NH₃) = -56.5577686 au
E(BH₃) = -26.6153236 au
E(NH₃BH₃) = -83.2246901 au
ΔE = E(NH₃BH₃) - [E(NH₃) + E(BH₃)] = -83.2246901 + 56.5577686 + 26.6153236 = -0.0515979 au = -135.47 kJmol^-1

Dissociation energy

ΔE = 135.47 kJmol^-1

Comparison with literature values

The final and association energies are compared with literature values below.

Compound	Computed final energies /au	Literature values of final energies /au		Calculated association energy /kJmol^-1	Literature values of association energy /kJmol^-1
Compound	DFT/6-31G(d;p)	HF/6-31G	DFT/NLSD	DFT/6-31G(d;p)	HF/6-31G	DFT/NLSD
NH₃	-56.5577686	-56.18436	-56.628757	-	-	-
BH₃	-26.6153236	-26.39001	-26.643 585	-	-	-
NH₃BH₃	-83.2246901	-82.61182	-83.331114	-135.47	-98.32	-154.39

Table 14. Comparison of energies of various compounds.

From Table 14, it is clear that the final energies of optimised structures of NH₃, BH₃ and NH₃BH₃ are highly similar to literature values regardless of the method and basis set used. This is surprising as it is commonly known that different method and basis set would lead to rather different results. However, the close agreement means that the optimised structures are most likely accurate.

However, the calculated association energy is quite different from the literature values. Given that the final energies of optimised structures are almost identical, this means that a simple manipulation of final energies to determine NH₃BH₃, as performed above, is insufficient. Instead, it is always better and recommended to compute the binding energy using Gaussian or similar softwares.

Third year Inorganic Computational Laboratory

Optimisation Analysis

Data

BH3 optimisation (3-21G)

BH3 optimisation (6-31G;d,p)

GaBr3 optimisation (LanL2DZ)

BBr3 optimisation (Gen)

Analysis: Comparison of bond distances

Frequency Data and Analysis

BH3 frequency (6-31G;d,p)

Data

3N-6 vibrational frequencies

IR vibrational frequencies

GaBr3 frequency (LanL2DZ)

Data

3N-6 vibrational frequencies

IR vibrational frequencies

Analysis of Vibrational Frequencies

Molecular Orbitals (MOs) of BH3

MO diagram

NBO analysis of NH3

NH3 optimisation (6-31G;d,p)

Data

NH3 frequency

Data

3N-6 vibrational frequencies

MO data of NH3

Data

NH3 Charge Distribution

Analysis of NH3BH3

NH3BH3 optimisation (6-31G;d,p)

Data

NH3BH3 frequency

Data

3N-6 vibrational frequencies

Association and dissociation energies of NH3BH3

Association energy

Dissociation energy

Comparison with literature values

BH₃ optimisation (3-21G)

BH₃ optimisation (6-31G;d,p)

GaBr₃ optimisation (LanL2DZ)

BBr₃ optimisation (Gen)

BH₃ frequency (6-31G;d,p)

GaBr₃ frequency (LanL2DZ)

Molecular Orbitals (MOs) of BH₃

NBO analysis of NH₃

NH₃ optimisation (6-31G;d,p)

NH₃ frequency

MO data of NH₃

NH₃ Charge Distribution

Analysis of NH₃BH₃

NH₃BH₃ optimisation (6-31G;d,p)

NH₃BH₃ frequency

Association and dissociation energies of NH₃BH₃