Rep:Mod:knobcreek
Physical Computational Chemistry - Experiment 3: The Transition State
Cope Rearrangement Tutorial
Introduction
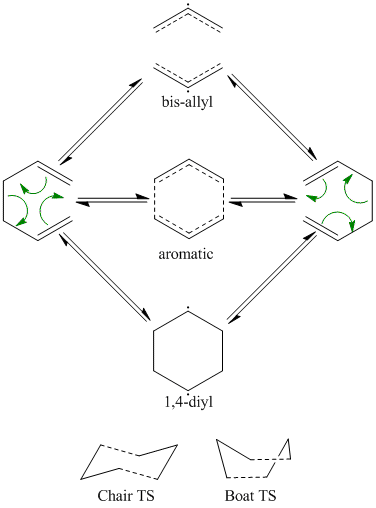
The cope rearragement is a [3,3] sigmatropic shift (3 atom group, "migrating" along another 3 atom group), that occurs in a concerted fashion, although for a time it was disputed as to whether it could be dissociative or stepwise.
Gaussian's capability in studying chemical reactivity will be explored and investigated using the Cope Rearrangement, specifically of 1,5 hexadiene, by probing the reaction pathway for low energy minima and transition structures (higher energy boat and chair), which should give a indication of the preferred reaction mechanism.
Optimizing the Reactants and Products
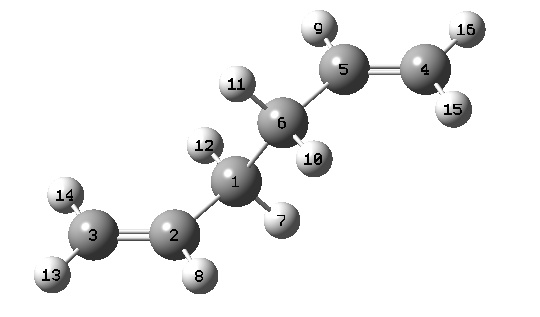
TThe structure of 1,5-Hexadiene was drawn in Gaussview in the anti and the gauche conformations for the central 4 atoms, with the expectation that gauche would have a higher energy conformation, "cleaned" and optimised using HF/3-21G (Hartree-Fock Method/3-21G Basis Set). The symmetries and energies of these were recorded, and are shown in the table below.
Upon inspection of Mod:phys3#Appendix_1, these were matched to the gauche 2 and anti 1 conformers, and the gauche conformation was indeed lower in energy.
An attempt was then made to find the lowest energy conformer of the molecule, and it was hypothesised that this would be the one with all the bonds anti and the double bound app to each other. This molecule was drawn, optimised using HF/3-21G and the energy and symmetry recorded. This was matched to the anti2 conformer in appendix 1. Suprisingly this was not the lowest energy conformer, and so a further 7 conformers were drawn and optimised, to give the remaining conformers to match the symmetry and energies of the given conformers in appendix 1.
The table below is laid out with the same referencing system as the above instructional link, but with JMol applet button embedded instead of image files:
| Conformer | Energy/ Hartrees (Max Decimal Places per Gaussview) | Energy/Hartrees (5dp) | Point Group | JMol Applet |
| Gauche 1 | -231.68771616 | -231.68772 | C2 | |
| Gauche 2 | -231.69166698 | -231.69167 | C2 | |
| Gauche 3 | -231.69266121 | -231.69266 | C1 | |
| Gauche 4 | -231.69153053 | -231.69153 | C2 | |
| Gauche 5 | -231.68961572 | -231.68962 | C1 | |
| Gauche 6 | -231.68916014 | -231.68916 | C1 | |
| Anti 1 | -231.69260214 | -231.69260 | C2 | |
| Anti 2 | -231.69253526 | -231.69254 | Ci | |
| Anti 3 | -231.68907063 | -231.68907 | C2h | |
| Anti 4 | -231.69097054 | -231.69097 | C1 |
It was suprising to see that the lowest energy conformer was in the gauche3 conformation as (based purely on a steric arguement) the anti conformer would be the one we would expect to be more stable. Base on this it is hypothesised that there must be other stabilising stereoelectronic interactions involving the π/π* double bond orbitals and the methylene C-H σ/σ* orbitals.
Another arguement is that the anti2 conformer is indeed lower energy, but as has been stated in the instructional, that the B3LYP/6-31G(d) method is a more accurate agreement with literature, perhaps if both molecules were calculated using that method, the anti2 would give a lower energy?
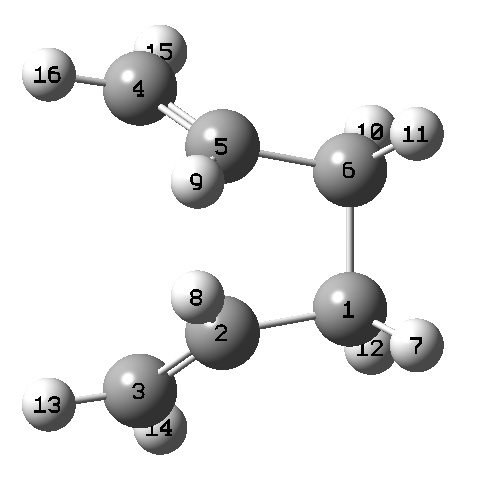
The anti2 conformer was then further optimised using the DFT B3LYP/6-31G(d) method and basis set. The energy of the molecules using the new method is -234.61127 Hartree cf. -231.69354 for HF/3-21G and both have the Ci point group.
The overall geometries were also compared to the HF/3-21 method. The following bond lengths and geometries have been extracted from the .LOG files, and can be correlated using the labelled diagram of the molecules:
----------------------------
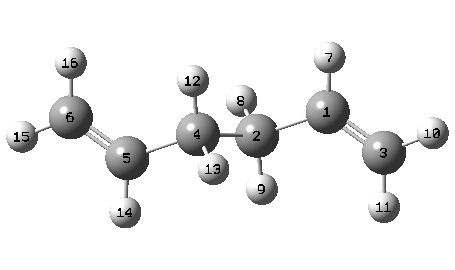
! Optimized Parameters !
! (Angstroms and Degrees) !
-------------------------- --------------------------
! Name Definition Value Derivative Info. !
--------------------------------------------------------------------------------
! R1 R(1,2) 1.5089 -DE/DX = 0.0 !
! R2 R(1,3) 1.3161 -DE/DX = 0.0 !
! R3 R(1,7) 1.0769 -DE/DX = 0.0 !
! R4 R(2,4) 1.5531 -DE/DX = -0.0001 !
! R5 R(2,8) 1.0855 -DE/DX = 0.0 !
! R6 R(2,9) 1.0848 -DE/DX = 0.0 !
! R7 R(3,10) 1.0734 -DE/DX = 0.0 !
! R8 R(3,11) 1.0747 -DE/DX = 0.0 !
! R9 R(4,5) 1.5089 -DE/DX = 0.0 !
! R10 R(4,12) 1.0848 -DE/DX = 0.0 !
! R11 R(4,13) 1.0855 -DE/DX = 0.0 !
! R12 R(5,6) 1.3161 -DE/DX = 0.0 !
! R13 R(5,14) 1.0769 -DE/DX = 0.0 !
! R14 R(6,15) 1.0734 -DE/DX = 0.0 !
! R15 R(6,16) 1.0747 -DE/DX = 0.0 !
! A1 A(2,1,3) 124.8118 -DE/DX = 0.0 !
! A2 A(2,1,7) 115.505 -DE/DX = 0.0 !
! A3 A(3,1,7) 119.6752 -DE/DX = 0.0 !
! A4 A(1,2,4) 111.3402 -DE/DX = 0.0 !
! A5 A(1,2,8) 109.9816 -DE/DX = 0.0 !
! A6 A(1,2,9) 109.9781 -DE/DX = 0.0 !
! A7 A(4,2,8) 108.3295 -DE/DX = 0.0 !
! A8 A(4,2,9) 109.3983 -DE/DX = 0.0 !
! A9 A(8,2,9) 107.7268 -DE/DX = 0.0 !
! A10 A(1,3,10) 121.8691 -DE/DX = 0.0 !
! A11 A(1,3,11) 121.8226 -DE/DX = 0.0 !
! A12 A(10,3,11) 116.308 -DE/DX = 0.0 !
! A13 A(2,4,5) 111.3402 -DE/DX = 0.0 !
! A14 A(2,4,12) 109.3983 -DE/DX = 0.0 !
! A15 A(2,4,13) 108.3295 -DE/DX = 0.0 !
! A16 A(5,4,12) 109.9781 -DE/DX = 0.0 !
! A17 A(5,4,13) 109.9816 -DE/DX = 0.0 !
! A18 A(12,4,13) 107.7268 -DE/DX = 0.0 !
! A19 A(4,5,6) 124.8118 -DE/DX = 0.0 !
! A20 A(4,5,14) 115.505 -DE/DX = 0.0 !
! A21 A(6,5,14) 119.6752 -DE/DX = 0.0 !
! A22 A(5,6,15) 121.869 -DE/DX = 0.0 !
! A23 A(5,6,16) 121.8226 -DE/DX = 0.0 !
! A24 A(15,6,16) 116.308 -DE/DX = 0.0 !
! D1 D(3,1,2,4) 114.6683 -DE/DX = 0.0 !
! D2 D(3,1,2,8) -125.2447 -DE/DX = 0.0 !
! D3 D(3,1,2,9) -6.7609 -DE/DX = 0.0 !
! D4 D(7,1,2,4) -64.2951 -DE/DX = 0.0 !
! D5 D(7,1,2,8) 55.7919 -DE/DX = 0.0 !
! D6 D(7,1,2,9) 174.2757 -DE/DX = 0.0 !
! D7 D(2,1,3,10) -179.0998 -DE/DX = 0.0 !
! D8 D(2,1,3,11) 1.1023 -DE/DX = 0.0 !
! D9 D(7,1,3,10) -0.1766 -DE/DX = 0.0 !
! D10 D(7,1,3,11) -179.9746 -DE/DX = 0.0 !
! D11 D(1,2,4,5) 180.0 -DE/DX = 0.0 !
! D12 D(1,2,4,12) 58.2335 -DE/DX = 0.0 !
! D13 D(1,2,4,13) -58.9415 -DE/DX = 0.0 !
! D14 D(8,2,4,5) 58.9415 -DE/DX = 0.0 !
! D15 D(8,2,4,12) -62.825 -DE/DX = 0.0 !
! D16 D(8,2,4,13) 180.0 -DE/DX = 0.0 !
! D17 D(9,2,4,5) -58.2336 -DE/DX = 0.0 !
! D18 D(9,2,4,12) 180.0 -DE/DX = 0.0 !
! D19 D(9,2,4,13) 62.8249 -DE/DX = 0.0 !
! D20 D(2,4,5,6) -114.6682 -DE/DX = 0.0 !
! D21 D(2,4,5,14) 64.2951 -DE/DX = 0.0 !
! D22 D(12,4,5,6) 6.761 -DE/DX = 0.0 !
! D23 D(12,4,5,14) -174.2757 -DE/DX = 0.0 !
! D24 D(13,4,5,6) 125.2448 -DE/DX = 0.0 !
! D25 D(13,4,5,14) -55.7919 -DE/DX = 0.0 !
! D26 D(4,5,6,15) 179.0998 -DE/DX = 0.0 !
! D27 D(4,5,6,16) -1.1023 -DE/DX = 0.0 !
! D28 D(14,5,6,15) 0.1767 -DE/DX = 0.0 !
! D29 D(14,5,6,16) 179.9746 -DE/DX = 0.0 !
--------------------------------------------------------------------------------
----------------------------
! Optimized Parameters !
! (Angstroms and Degrees) !
-------------------------- --------------------------
! Name Definition Value Derivative Info. !
--------------------------------------------------------------------------------
! R1 R(1,2) 1.5041 -DE/DX = 0.0001 !
! R2 R(1,3) 1.3335 -DE/DX = 0.0 !
! R3 R(1,7) 1.0919 -DE/DX = 0.0 !
! R4 R(2,4) 1.5481 -DE/DX = 0.0 !
! R5 R(2,8) 1.0997 -DE/DX = 0.0 !
! R6 R(2,9) 1.098 -DE/DX = 0.0 !
! R7 R(3,10) 1.0868 -DE/DX = 0.0 !
! R8 R(3,11) 1.0885 -DE/DX = 0.0 !
! R9 R(4,5) 1.5041 -DE/DX = 0.0001 !
! R10 R(4,12) 1.098 -DE/DX = 0.0 !
! R11 R(4,13) 1.0997 -DE/DX = 0.0 !
! R12 R(5,6) 1.3335 -DE/DX = 0.0 !
! R13 R(5,14) 1.0919 -DE/DX = 0.0 !
! R14 R(6,15) 1.0868 -DE/DX = 0.0 !
! R15 R(6,16) 1.0885 -DE/DX = 0.0 !
! A1 A(2,1,3) 125.2999 -DE/DX = 0.0 !
! A2 A(2,1,7) 115.74 -DE/DX = 0.0 !
! A3 A(3,1,7) 118.9559 -DE/DX = 0.0 !
! A4 A(1,2,4) 112.6805 -DE/DX = 0.0 !
! A5 A(1,2,8) 109.7755 -DE/DX = 0.0 !
! A6 A(1,2,9) 109.7445 -DE/DX = 0.0 !
! A7 A(4,2,8) 108.1978 -DE/DX = 0.0 !
! A8 A(4,2,9) 109.6113 -DE/DX = 0.0 !
! A9 A(8,2,9) 106.64 -DE/DX = 0.0 !
! A10 A(1,3,10) 121.8628 -DE/DX = 0.0 !
! A11 A(1,3,11) 121.6602 -DE/DX = 0.0 !
! A12 A(10,3,11) 116.4764 -DE/DX = 0.0 !
! A13 A(2,4,5) 112.6805 -DE/DX = 0.0 !
! A14 A(2,4,12) 109.6113 -DE/DX = 0.0 !
! A15 A(2,4,13) 108.1978 -DE/DX = 0.0 !
! A16 A(5,4,12) 109.7445 -DE/DX = 0.0 !
! A17 A(5,4,13) 109.7755 -DE/DX = 0.0 !
! A18 A(12,4,13) 106.64 -DE/DX = 0.0 !
! A19 A(4,5,6) 125.2999 -DE/DX = 0.0 !
! A20 A(4,5,14) 115.74 -DE/DX = 0.0 !
! A21 A(6,5,14) 118.9559 -DE/DX = 0.0 !
! A22 A(5,6,15) 121.8628 -DE/DX = 0.0 !
! A23 A(5,6,16) 121.6602 -DE/DX = 0.0 !
! A24 A(15,6,16) 116.4764 -DE/DX = 0.0 !
! D1 D(3,1,2,4) 118.5983 -DE/DX = 0.0 !
! D2 D(3,1,2,8) -120.742 -DE/DX = 0.0 !
! D3 D(3,1,2,9) -3.8468 -DE/DX = 0.0 !
! D4 D(7,1,2,4) -60.6403 -DE/DX = 0.0 !
! D5 D(7,1,2,8) 60.0194 -DE/DX = 0.0 !
! D6 D(7,1,2,9) 176.9146 -DE/DX = 0.0 !
! D7 D(2,1,3,10) -179.5939 -DE/DX = 0.0 !
! D8 D(2,1,3,11) 0.6885 -DE/DX = 0.0 !
! D9 D(7,1,3,10) -0.3777 -DE/DX = 0.0 !
! D10 D(7,1,3,11) 179.9046 -DE/DX = 0.0 !
! D11 D(1,2,4,5) 180.0 -DE/DX = 0.0 !
! D12 D(1,2,4,12) 57.4801 -DE/DX = 0.0 !
! D13 D(1,2,4,13) -58.4407 -DE/DX = 0.0 !
! D14 D(8,2,4,5) 58.4407 -DE/DX = 0.0 !
! D15 D(8,2,4,12) -64.0792 -DE/DX = 0.0 !
! D16 D(8,2,4,13) 180.0 -DE/DX = 0.0 !
! D17 D(9,2,4,5) -57.4801 -DE/DX = 0.0 !
! D18 D(9,2,4,12) 180.0 -DE/DX = 0.0 !
! D19 D(9,2,4,13) 64.0792 -DE/DX = 0.0 !
! D20 D(2,4,5,6) -118.5983 -DE/DX = 0.0 !
! D21 D(2,4,5,14) 60.6403 -DE/DX = 0.0 !
! D22 D(12,4,5,6) 3.8468 -DE/DX = 0.0 !
! D23 D(12,4,5,14) -176.9146 -DE/DX = 0.0 !
! D24 D(13,4,5,6) 120.742 -DE/DX = 0.0 !
! D25 D(13,4,5,14) -60.0194 -DE/DX = 0.0 !
! D26 D(4,5,6,15) 179.5939 -DE/DX = 0.0 !
! D27 D(4,5,6,16) -0.6885 -DE/DX = 0.0 !
! D28 D(14,5,6,15) 0.3777 -DE/DX = 0.0 !
! D29 D(14,5,6,16) -179.9046 -DE/DX = 0.0 !
--------------------------------------------------------------------------------
As we can see, there are only minor changes in the geometry of the molecules.
This new optimised structure was then run through Gaussian again, but instructed to calculate frequency vibrations as well. Upon completion of the calculation, the vibrations were inspected to ensure that there were no negative frequencies (implying an unoptimised structure). This addition to the calculation gave further thermochemistry data, as extracted from the .LOG file:
Sum of electronic and zero-point Energies= -234.469212 Sum of electronic and thermal Energies= -234.461854 Sum of electronic and thermal Enthalpies= -234.460910 Sum of electronic and thermal Free Energies= -234.500840
The first two values are in very good agreement to the available values in Mod:phys3#Results_Table, as is the electronic energy of -234.61127 Hartree stated earlier (this value is viewed in results summary).
As a side note, the energies were calculated at 0 Kelvin using the advanced gaussview tutorial to yield:
Sum of electronic and zero-point Energies= -234.468775 Sum of electronic and thermal Energies= -234.461427 Sum of electronic and thermal Enthalpies= -234.460483 Sum of electronic and thermal Free Energies= -234.500391
Optimizing the "Chair" and "Boat" Transition Structures
The sections shows different methods in calculating trasition structure optimisations, namely:
- computing the force constants at the beginning of the calculation.
- using the redundant coordinate editor.
- using QST2.
- as an advance, using QST3 method.
The reaction co-ordinate will also be followed by using an IRC calculation, and then calculting activation energies for the Cope rearrangement via both the chair and boat TSs.
Drawing and Optimising the Allyl Fragment
Firstly an allyl fragment (C3H5) was drawn and optimised using the HF/3-21G level of theory to give:
The optimised energy was 115.823 Hartree.
Optimising The Chair TS Using TS(Berny)
This fragment was then copied twice in to a new MolGroup, and arranged in an approximation of the chair TS with the terminal carbons of each molecule 2.2Å from each other (achieved using the modify bond tool):
A Opt+Freq Transition State calculation was carried out to a TS(Berny) (NOT A MINIMUM) at the HF/3-21g level of theory. A search for a TS implies that the program is seeking a maximum cf. a minimum for an energy minima optimisation. As a result, negative frequencies are possible and so the Opt=NoEigen is additionally added to the input code, stopping the calculation terminating unsuccessfully due to the calculation of more than one negative frequency.
The energy of the optimised TS is -231.619 Hartree and has a negative vibration -817.946cm-1 with terminal carbon to terminal carbon bond lengths of 2.01948Å and 2.02008Å. The Jmol for the optimised structure and the negative vibrational mode is shown:
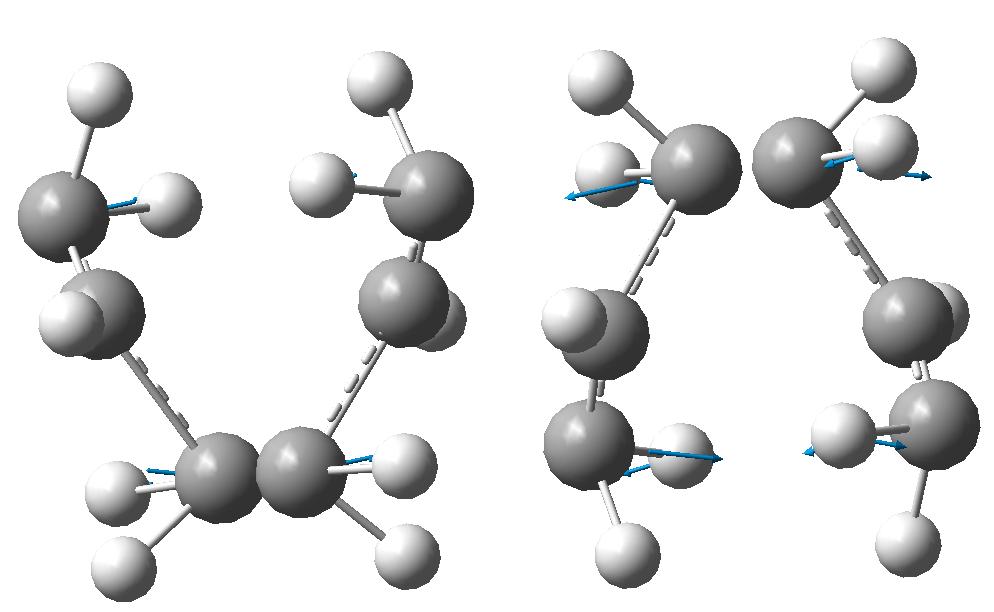
Optimising The Chair TS Using Frozen Co-Ord Method
Using the same starting guess TS structure as earlier, the "redundant coord editor" from the edit menu was used to select two corresponding terminal carbons on the allyl fragements that are breaking/forming during the rearrangement, these co-ordinates are then frozen as bonds. This structure was then optimised as a minimum using HF/3-21G.
The structure achieved is similar to the earlier method and has boond lengths 2.21259Å and 2.20000Å and energy -231.61493 Hartree. This structure is then optimised further using the same process, but "freeze derivative" instead of "freeze bond" and using TS(berny):
With bond lengths 2.02083Å and 2.02159Å, energy -231.61932Å Hartree and an imaginary frequency of -817.9cm-1, which animates in a very similar manner to the the one illustrated earlier.
It is interesting to note that with "# opt freq hf/3-21g geom=connectivity" instead of "# opt=(ts,modredundant,noeigen) freq hf/3-21g geom=connectivity" in the .gjf input file, the TS optimises as shown here:
With energy -231.69167 Hartree and one "terminal" bond length of 1.55065Å and the other 4.39047Å, this is very similar to the product in terms of bond lengths and shows it is a minimum (optimisation) not TS by the fact that it has no negaitve vibration frequencies. However the energy is still similar!
Optimising the Boat TS Using QST2 Method
The QTS2 method is very interesting since it has the ability to look at a starting point and an end point, and by interpolating between then, calculate the TS. The anti2 conformer was pasted twice into the same file as two separate molgroups. It was necessary to number the "reactant" and "product". This is carried out in the "view"->"labels" window to give:
|
|
|
| Reactant | Product |
The job type was selected as opt+freq and optimised to a TS(QTS2). This job failed, and the resultant molecule was given:
This occured due to the calculation method's inability to consider rotation around the central C-C bond, and working by simply translating the allyl fragments. This resulted in an output similar to the Boat TS, but further apart and with the terminal acrbons linking to the terminal carbons at the opposite end of each molecule! (4.52205Å and 3.52460Å).
This resulted in the need to modify the reactant and product to bring them closer to the boat TS. The 4 central carbon dihedral angles are changed to 0° and the two inside C-C-C angles to 100°, to give the following:
|
|
|
| Reactant | Product |
The QTS2 calculation was run again with the new conformations, and gave the following output:
With an energy of -231.60280 Hartree and a imaginary vibration of -840.166cm-1 shown as:
Intrinsic Reaction Co-ordinate
This method is able to connect conformers of reactant and product, via the chair or boat TS. It follows the steepest paths along the PES using small geometry changes. The TS(Berny) optimised chair TS was used to follow the reaction path.
The job type selected was IRC following the reaction forwards only (due to reaction symmetry)with the HF/3-21G methods over n=50 points. This gave the following:
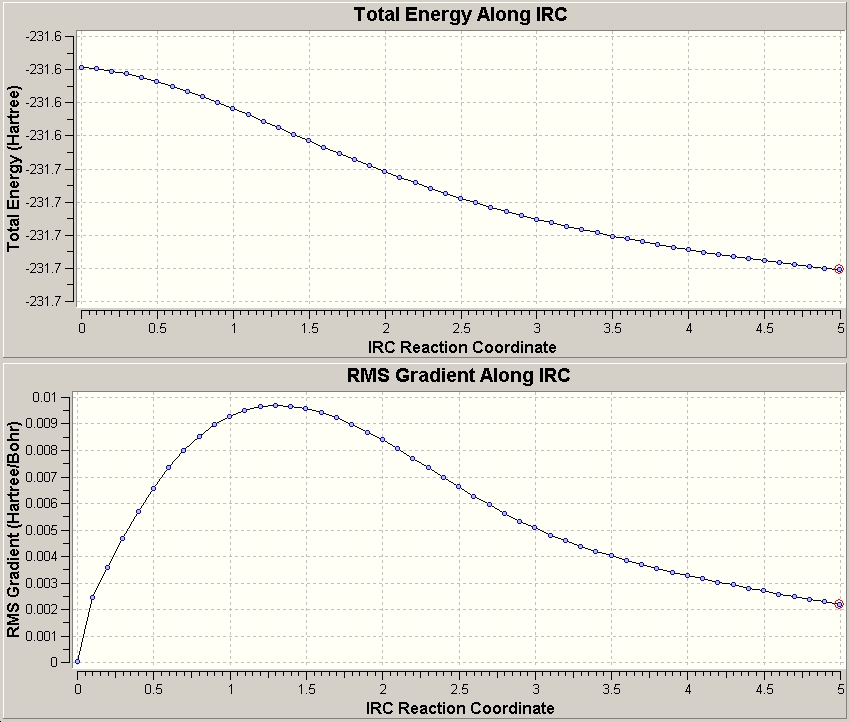
We can see here that at the 50th point the RMS gradient≠0, signifying that the calculation has not reached a minimum. This can however be achieved in three ways:
- Take last IRC point, and run an ordinary optimisation.
- Take more steps.
- Calculate force constants at every step rather than just the start.
The ordinary HF/3-21G optimisation gave the following structure with energy-231.69167 Hartree and C2 symmetry:
Taking more steps (n=200) gave the following, which seemed to optimise (according to the molgroup number) at n=100, since there were no more frames:
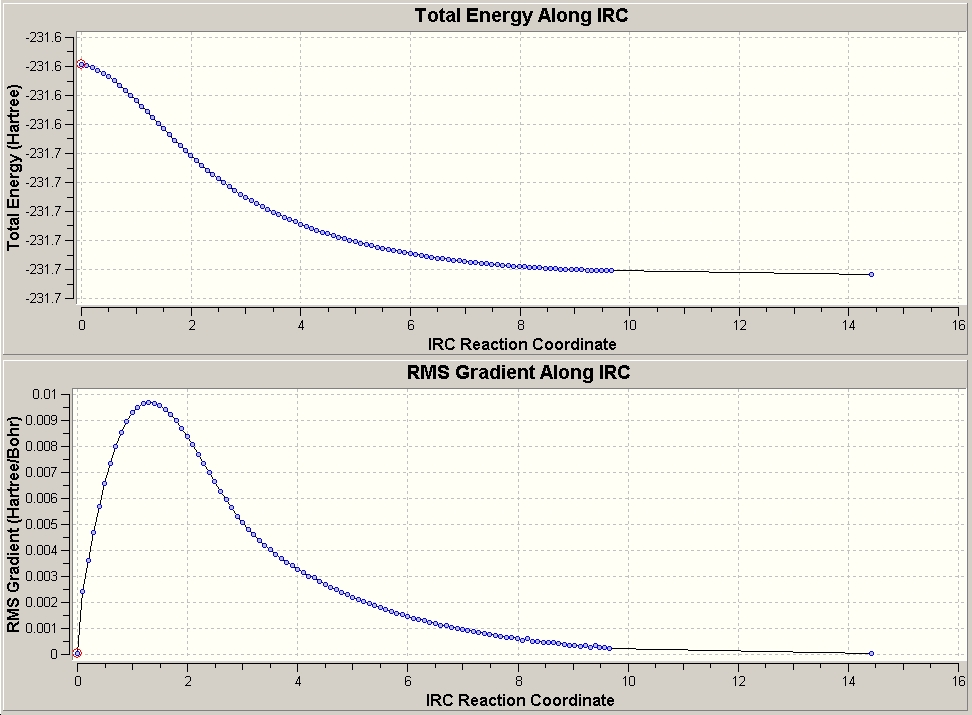
This had the energy -231.69163 Hartree with a symmetry of C1, but with looser tolerances (and by qualitative vidual analysis) would be a C2. Also, we can see from the graph that this has reached a minimum.
Finally, the method of calculating the force constants at every step gave:
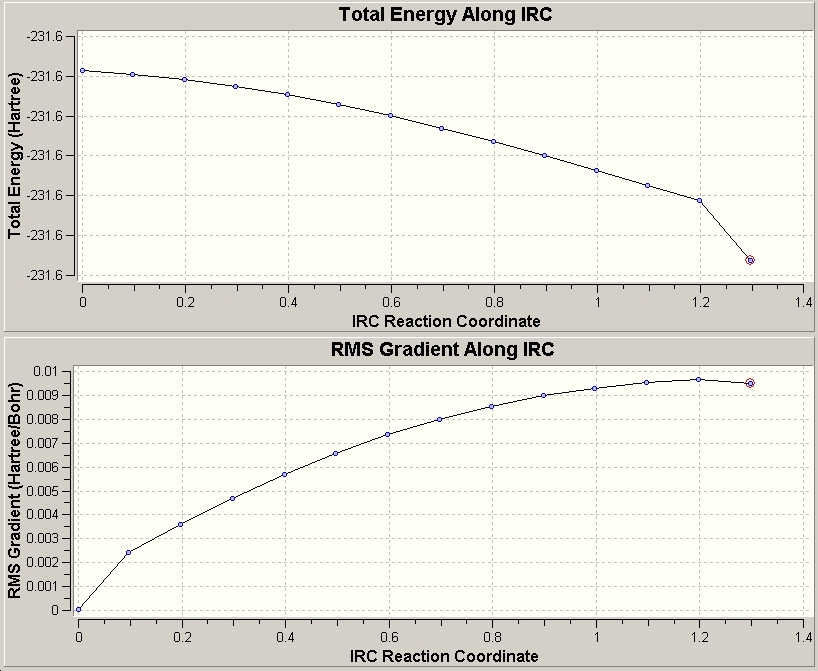
This had an energy of -231.643140 Hartree, with a C2 symmetry. However the graphs indicate that the molecule has not optimsied due to the increasing RMS gradient value! However, strangely, the energy is decrease. This would imply that the energy of succesive structures is decreasing at an accelerating rate. Also, the calculation seemed to stop at 14 points, rather than the 50 specified. This could warrant further work (time permitting).
Calculating the Activation Energies
The transition states optimised with HF/3-21G were taken and reoptimised to the higher level B3LYP/6-31G*:
A comparison of the energies and some key bond angles is shown below:
| Chair | Boat | |||
|---|---|---|---|---|
| HF/3-21G | B3LYP/6-31G* | HF/3-21G | B3LYP/6-31G* | |
| Energy (Hartree) | -231.61932 | -234.55698 | -231.60280 | -234.54309 |
| Fragment Distance/Å | 2.01948,2.02008 | 1.96757, 1.96757 | 2.14001 | 2.20663 |
| C-C-C Bond Angles/° | 120.491,120.492 | 119.954 | 121.681 | 122.270 |
| Imaginary Vibration/cm-1 | -817.946 | -565.545 | 840.166 | -530.362 |
We can see that the geometries have not changed significantly, however the energies have! To put this in perspective, for the Chair TS the energy has lowered 7712.8 kJ/Mol and the Boat TS has lowered by 7722.7kJ/Mol.
The energies below were extracted from .LOG files, the Results Summaries, and zero point corrections made using OptFreq:
| HF/3-21G | HF/3-21G | HF/3-21G | B3LYP/6-31G* | B3LYP/6-31G* | B3LYP/6-31G* | |
|---|---|---|---|---|---|---|
| Electronic Energy | Sum of Electronic and Zero Point Energies | Sum of Electronic and Thermal Energies | Electronic Energy | Sum of Electronic and Zero Point Energies | Sum of Electronic and Thermal Energies | |
| at 0K | at 298.15K | at 0K | at 298.15K | |||
| Chair TS | -231.619322 | -231.466694 | -231.461336 | -234.556983 | -234.414930 | -234.409009 |
| Boat TS | -231.602802 | -231.450924 | -231.445294 | -234.543093 | -234.402339 | -234.396008 |
| Reactant (anti2) | -231.692535 | -231.539541 | -231.532567 | -234.611715 | -234.469211 | -234.461427 |
The activation energies at 0 Kelvin and 1 atm and at 298.15K were calculated and compared to the literature values. Values at 0K were calculated using the OptFreq method through Gaussian 03W.
| HF/3-21G | HF/3-21G | B3LYP/6-31G* | B3LYP/6-31G* | Expt | |
|---|---|---|---|---|---|
| at 0K | at 298.15K | at 0K | at 298.15K | 0K | |
| ΔE (Chair) | 45.71 | 44.70 | 34.06 | 32.89 | 33.5+/-0.5 |
| ΔE (Boat) | 55.61 | 54.76 | 41.96 | 41.05 | 44.7+/-0.5 |
It is clear that the activation energies are a much better match using the B3LYP/6-31G(d) method and basis set. The Boat activation energy at 0K is much further away from the experimental values however, suggesting that the boat structure is not in line with the actual real boat structure seen experimentally.
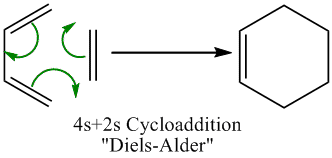
The Diels Alder Cycloaddition
The diels alder cycoaddition for ethene and butadiene proceeds as follows:
Optimising Butadiene
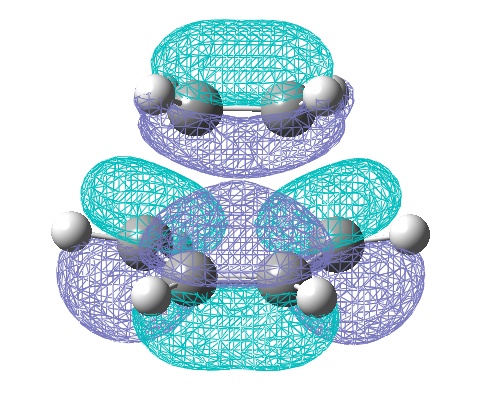
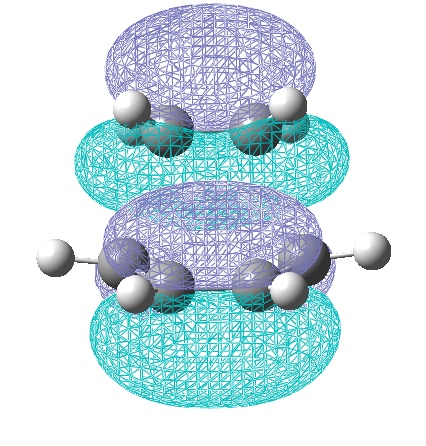
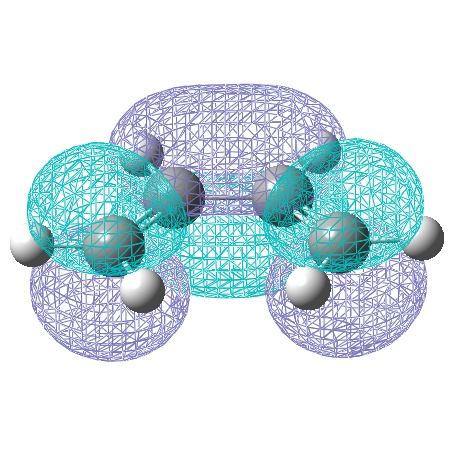
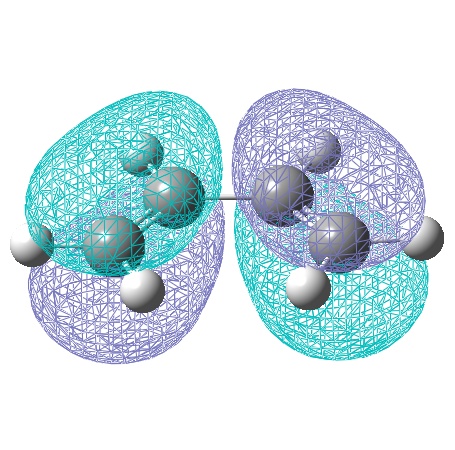
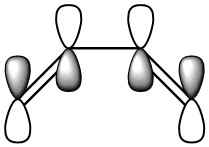
The cis-butadiene molecule was drawn in gaussview and optimised using the semi-empirical AM1 method, generating the following MOs:
| LUMO | HOMO |
|---|---|
 |
 |
 |
 |
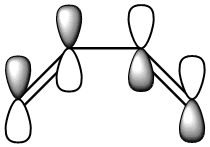| Symmetric with respect to a vertical plane. | Anti-Symmetric with respect to a vertical plane. |
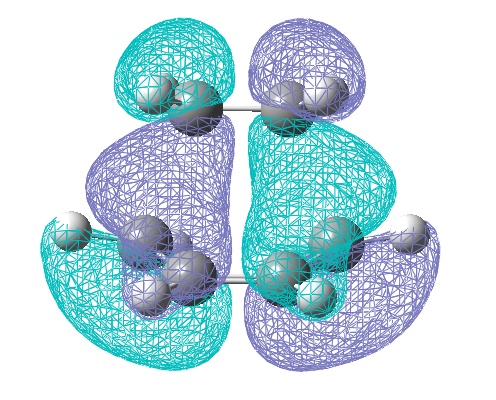
And the same calculation was carried out for ethylene:
| LUMO | HOMO |
|---|---|
 |
 |
|
|
| Anti-Symmetric with respect to a vertical plane. | Symmetric with respect to a vertical plane. |
The anti-symmetric and symmetric is assigned based on whether there is phase change upon reflection in the plane. Anti-symmetric shows a phase change, symmetric does not.
The Transition State and The Nature of the Reaction Path
To guess a tarnsition structure, the cyclohexene structure was drawn with a bridging -CH2-CH2- to create a bicyclo sysytem and optimised to the HF/3-21G level to give. One of the -CH2-CH2- bridges was then removed from the structure, and the bonds linking the remaining bridge to the molecule replaced with hydrogens. The distance between the two fragments was then set to 2.2Å. To confirm that this is indeed a transition state, the above guessed TS was optimised using HF/3-21G, TS(Berny) and "opt=noeigen". This gave the following optimised structure and negative vibration at -955.779 cm-1:
The was then reoptimised at the HF/3-21G to give a optimised TS with a negative vibration of -818.292cm-1 and the following structure:
The vibrations are both synchronous with respect to the vibration, and hence synchronous bond formation. The first real vibration is asymmetric.
A comparison of the bond distances and energies was carried out:
| Interfragment Distances/Å | sp2 bond lengths/Å | sp3 bond lengths (C2H4 Frag)/Å | sp3 bond lengths (C4H6)/Å | Energies (Hartree) | |
|---|---|---|---|---|---|
| Unoptimised Structure | 2.2, 2.09867 | 1.31925 | 1.55975 | 1.51385,1.51385 | N/A |
| Semi-Empirical AM1 | 2.11924, 2.11918 | 1.39746 | 1.38296 | 1.38190,1.38189 | 0.11162894 |
| HF/3-21G | 2.20959, 2.20969 | 1.3945 | 1.37589 | 1.37029,1.36991 | -231.6032084 |
The van der waals radius of the carbon atom is 1.70Å [1]. The forming bond lengths are very similar in each method, (and between the methods as well), highlighting the synchronous nature of bond formation. The forming σ bonds have lengths much greater than other sp3 bond lengths in the structure, but are still less than 2x1.70Å implying a weak bonding interaction (as expected in a TS).
There is an extremely large difference in Energies, but a fairly good match in geometries.
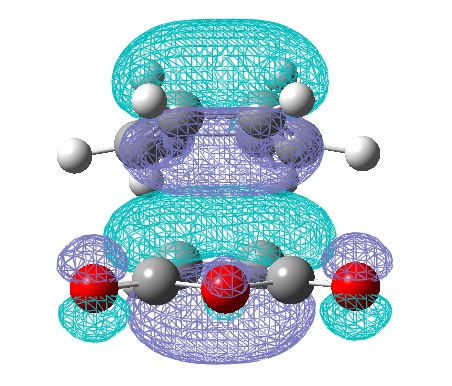
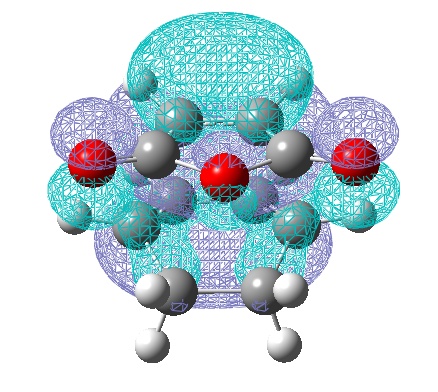
To begin with the AM1 generated MOs are illustrated and analysed below:
| LUMO | HOMO |
|---|---|
 |
 |
| Symmetric with respect to a vertical plane. | Anti-symmetric with respect to the plane. The two fragments show an interaction by an area of shared electron density, seemingly between the HOMO of butadiene and the LUMO of ethene, both of which have the same symmetry; a requirement for overlap. |
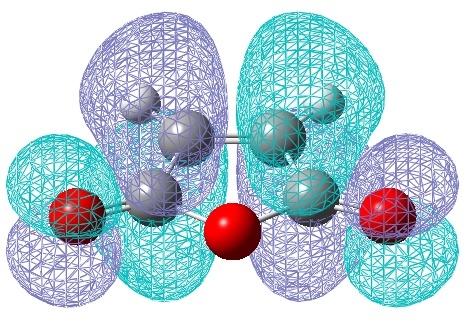
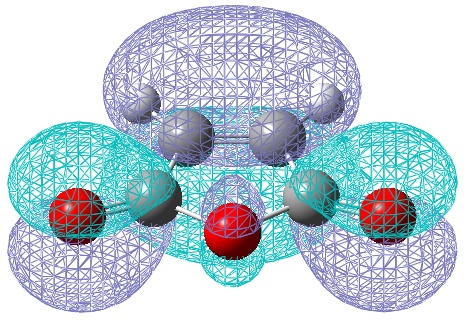
However, the calculations from the HF/3-21G method gave a much better (electronic) energy value, and would indicate more accurate electronic (and hence MO) analysis. Therefore the HOMO and LUMO via this method are also shown:
| LUMO | HOMO |
|---|---|
 |
 |
| Symmetric with respect to a vertical plane. | Anti-symmetric with respect to the plane. The two fragments show an interaction by an area of shared electron density, seemingly between the HOMO of butadiene and the LUMO of ethene, both of which have the same symmetry, a requirement for overlap. |
One of the most obvious changes is the change in symmetry of the HOMO to symmetric, however there is no change in symmetry for the LUMO. There is a small change in the LUMO, whereby it shows a constructing interaction, between the HOMO of ethene and the LUMO of butadiene! Once again symmetry rules have been obeyed.
Studying the regioselectivity of the Diels Alder Reactio - Maleic Anhydride
With substituted dienes and dienophiles, the diels alder reaction begins to show changes in selectivity, sometimes towards the thermodynamically less stable endo product (depending on the orientation of the approaching reactants). This is shown in the dimerisation of cyclopentadiene Mod:woodfordreserve#The_Hydrogenation_of_the_Cyclopentadiene_Dimer, where a favourable secondary orbital interaction occurs between the non-reacting п double bond in the dienophile cyclopentadiene, and the p orbitals of the C2 and C3 p orbitals on the diene. This lowers the energy of the transition state, making it the more easily accessible reaction pathway, the kinetic pathway.
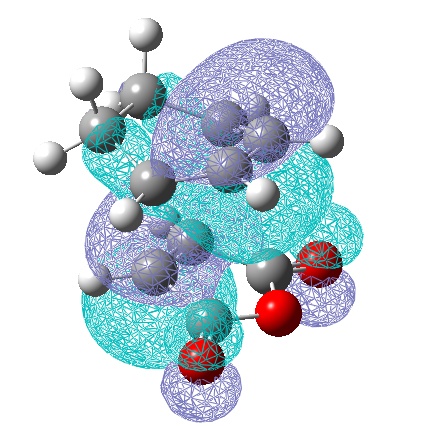
Here we shall look at the cycloaddition reaction of the diene 1,3-hexadiene and the dienophile maleic anhydride. First a rough guess of the transition states was carried out by drawing the two fragments and optimising them to HF/3-21G separately, giving the following MOs:
| LUMO | HOMO |
|---|---|
 |
 |
| LUMO | HOMO |
|---|---|
 |
 |
These were then putting them togther in one molgroup at a 2.2Å distance where the new bonds will form. This was done in an approximation to the endo and exo TS:
These two fragment transition states were then optimised to the Semi-Emprirical AM1 level to give the following molecules:
Deeming this level of optimisation to be indsufficient, further calculations were carried out at the HF/3-21G level:
A comparison of the bond lengths, energies and vibrations:
| Endo/Exo? | Forming C-C Bond Distances | Imaginary Frequency/cm-1 | Energies (Hartree) | |
|---|---|---|---|---|
| Unoptimised Structure | Endo | 2.24322, 2.20000 | ||
| Exo | 2.08431, 2.20000 | |||
| Semi-Empirical AM1 | Endo | 2.16252, 2.16236 | -805.609 | -0.0515943 |
| Exo | 2.17045, 2.17043 | -811.486 | -0.05050324 | |
| HF/3-21G | Endo | 2.23101, 2.23093 | -643.561 | -605.6103682 |
| Exo | 2.26065, 2.26081 | -647.464 | -605.6035912 |
It was deemed unnecessary to reproduce images of the imaginary vibrations, sufficed to say that the vibrations were along the newly forming σ bond and were synchronous in the same fashion as the bond formation.
The above values agree with the theory in that all the newly forming bond lengths are similar (within each calculation set) supporting evidence of a concerted reaction. The energies also show some good agreement from a qualitative perspective, in that the lower energy TS (the TS for the kinetic pathway) in each calculation set is the TS for the endo product.
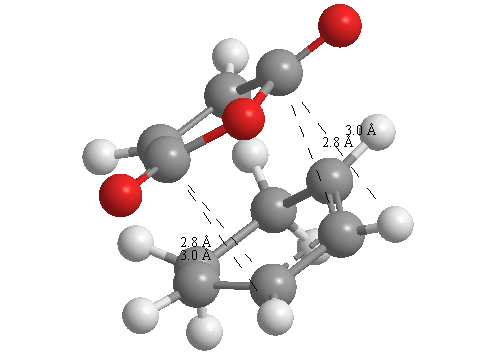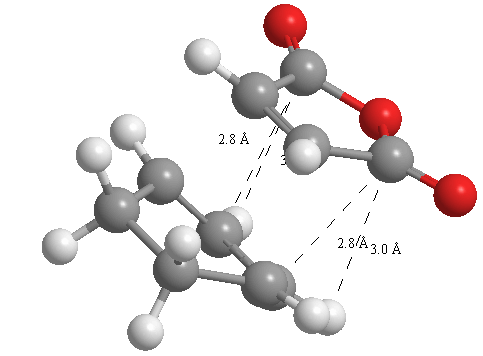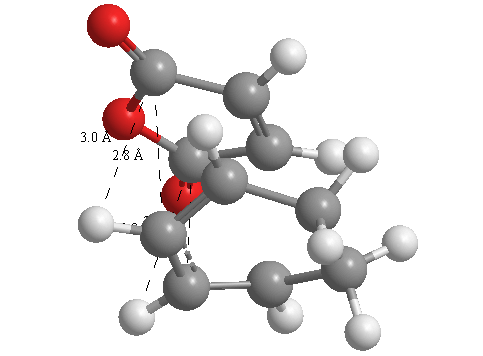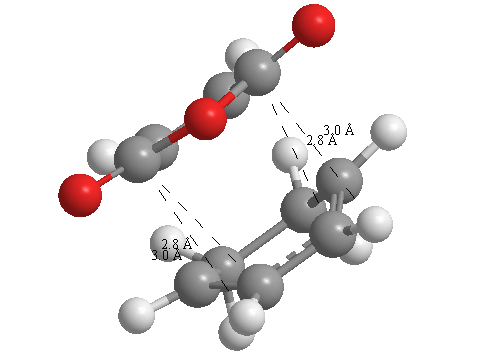
A further set of interfragment throughspace measurements (albeit only to 2 sf) were measured and are illustrated below. In each case there are two pairs of values. In the case of the exo TS, the larger measurements correspond to measurements from O=C-O-C=O carbons to the carbons on the opposite -CH2-CH2- section and the shorter pair of values correspond to a throughspace measurement from the O=C-O-C=O carbons to the hydrogens on the opposite -CH2-CH2- section.
| Endo | Exo |
|---|---|
 |
 |
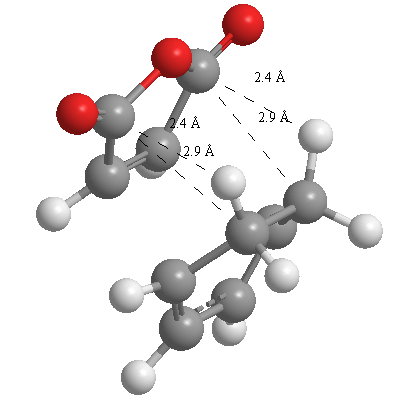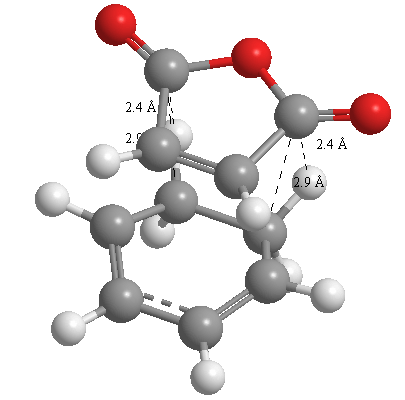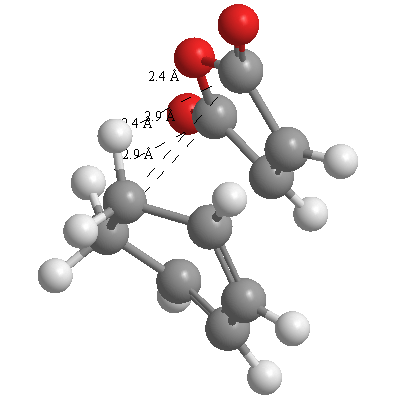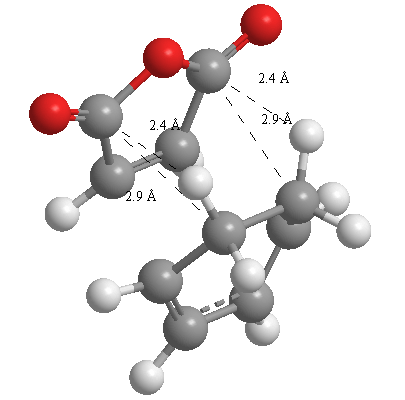| 2.8478Å, 2.8478Å, 2.9700Å and 2.9698Å | 2.9163Å, 2.9164Å, 2.4259Å and 2.4260Å |
In the endo TS the larger measurements correspond to the O=C-O-C=O carbons to the hydrogens on the opposite -CH-CH- section and the smaller measurements to the distance from the the O=C-O-C=O carbons to the carbons on the opposite -CH-CH-.
These measurements highlight the higher strain on the exo TS cf. the endo TS, even though the maleic anhydride sits closer to the main body of the opposite fragment ring in the the endo TS, due to the non-planarity of the "opposite" structure section in the exo TS, causing (albeit small) clash with the very nearby hydrogens. There is also
Now a set of frontier orbitals were generated for boths the exo and endo transition state, for both methods
| LUMO | HOMO |
|---|---|
 |
 |
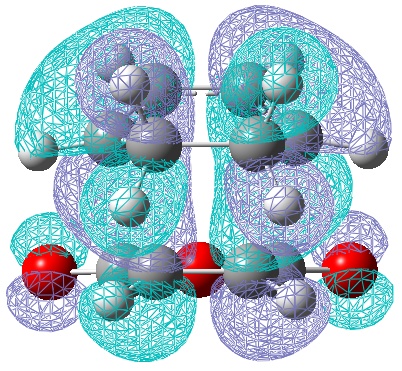| Anti-Symmetric with respect to a vertical plane. | Anti-symmetric with respect to the plane. |
| LUMO | HOMO |
|---|---|
 |
 |
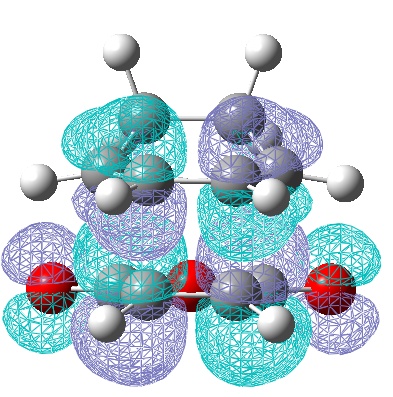| Anti-Symmetric with respect to a vertical plane. | Anti-symmetric with respect to the plane. |
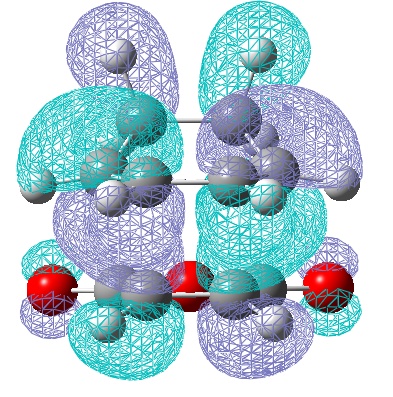
| LUMO | HOMO |
|---|---|
 |
 |
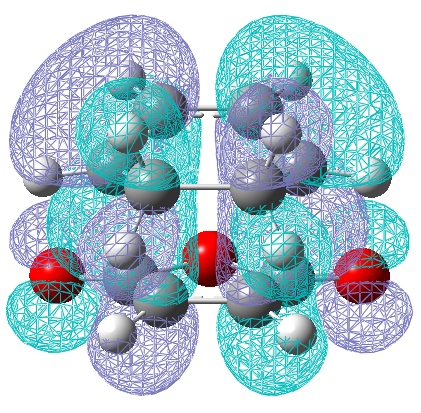| Anti-Symmetric with respect to a vertical plane. | Anti-symmetric with respect to the plane. |
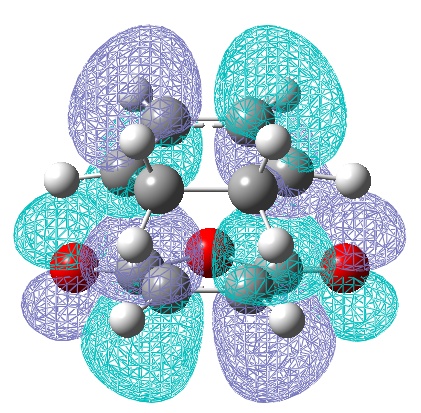
| LUMO | HOMO |
|---|---|
 |
 |
| Anti-Symmetric with respect to a vertical plane. | Anti-symmetric with respect to the plane.
|
The change in calculation method suprisingly showed very little change in the the visual structure of the MOs! This is in stark contrast (and hence suprising) when compared to the earlier excercise for butadiene and ethene where one of the HOMOs changed symmetry and shape!
The overall symmetry and shape of the MOs is also suprising in one other respect; the frontier orbitals do not show the secondary overlap (explained in the introduction to this section) that would stabilise the approach to the endo TS and final structure,in fact they show the presence of a node! It appears that in the case of the calculated MOs this stabilisation theory (discussed here Mod:woodfordreserve#The_Hydrogenation_of_the_Cyclopentadiene_Dimer) breaks down!
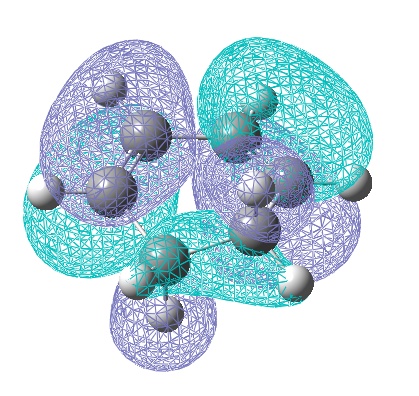
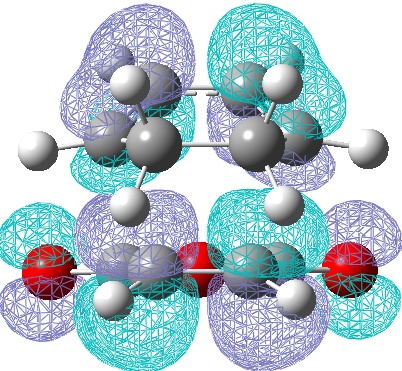
However the theory suggest this secondary orbital overlap is still present, as do the experimental outcomes. So the HOMO-1 orbitals of the transition states were computed:
| AM1 | HF/3-21G |
|---|---|
 |
 |
| AM1 | HF/3-21G |
|---|---|
|
 |
These clearly show a greater area of electron density between the diene and the EWG O=C-O-C=O area on the dienophile, giving some support to the secondary overlap theory.
References
- ↑ Bondi, A. (1964). "Van der Waals Volumes and Radii". J. Phys. Chem. 68 (3): 441–51 DOI:10.1021/j100785a001