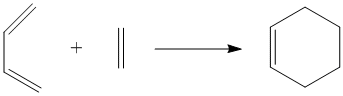Rep:Mod:kmt07233

The Cope Rearrangement of 1,5-hexadiene

The Cope Rearrangement of 1,5-hexadiene is an example of a [3,3]-sigmatropic shift rearrangement and is shown in the diagram below. The starting reactant and product of the rearrangement, 1,5-hexadiene , can have two possible forms: the anti and the gauche form. Both these forms are optimised in this computational experiment and their energy levels are compared. The possible transition states (boat or chair) involved in this rearrangement are also optimised and their energy levels calculated. After that, the activation energies for the Cope Rearrangement via these transition states are calculatd and compared to determine the preferred reaction mechanism for the rearrangement.

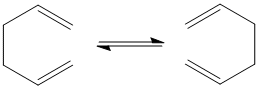
Optimisation of Reactants and Products

The Anti and Gauche Form of 1,5-hexadiene

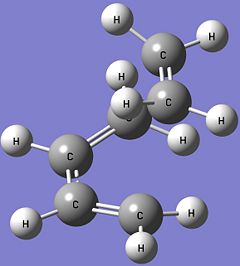
The anti form of 1,5-hexadiene (antiperiplanar conformation at the central four C atoms) is constructed in Gaussview and optimised using the Hartree Fock method with the 3-21G basis set. The optimised structure of this anti 1,5-hexadiene has the C₂ point group and its energy is calculated to be -231.69260235 Hartrees. Comparing this optimised structure with the structures given in Appendix 1, it is found that the optimised structure obtained is in fact the anti1 form (the obtained structure is actually the mirror image of the one structure given). There is a very good match between the calculated energy of the optimised structure with the one given in Appendix 1 (-231.69260 Hartrees) and the point groups are the same. This confirms that the optimised structure obtained is the anti1 form. The anti1 optimised structure is shown below. Anti1: https://www.ch.imperial.ac.uk/wiki/images/c/cb/KHAIMING_REACT_ANTI.LOG

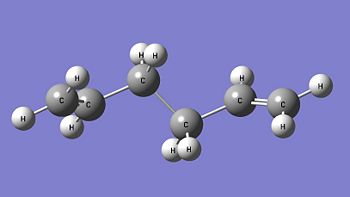
Another 1,5-hexadiene molecule, now with a gauche linkage at the central four C atoms, is drawn and optimised using the same method and basis set (HF/3-21G). This gauche form of 1,5-hexadiene is expected to have a higher energy level than the anti form that is optimised earlier as the gauche form is expected to be less stable due to the steric repulsion between the two R groups (-CHCH₂) when looking at the C₃-C₄ bond. After optimisation, the gauche form is calculated to have an energy of -231.69153035 Hartrees and its point group is found to be C₂. Using Appendix 1, the optimised gauche form obtained is determined to be the gauche4 form (the obtained structure is actually the mirror image of the structure in the appendix) with a very good match between their calculated energies (-231.69153 Hartrees) and point group. Comparing the energies between the anti1 form and the gauche4 form, it is found that the gauche4 form has higher energy (more positive value) than the anti1 form and this is in agreement with the earlier prediction. The gauche4 optimised structure is given below. Gauche4: https://www.ch.imperial.ac.uk/wiki/images/8/80/KHAIMING_REACT_GAUCHE.LOG

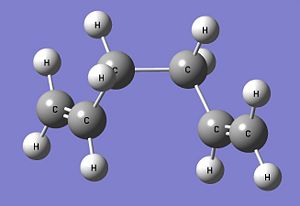
The lowest energy conformation of 1,5-hexadiene is predicted to be in the anti form as the two R groups (-CHCH₂) when looking at the C₃-C₄ bond are directed away from each other with an angle of about 180°, hence, reducing the amount of steric repulsion present in the anti form. This stabilises the anti form, causing the anti form to have a lower energy level. The gauche form as mentioned earlier is expected to experience a significant amount of steric repulsion between the R groups, hence, it is expected to be higher in energy. To prove this prediction, some possible anti and gauche forms are optimised at the HF/3-21G theory level and their energies and compared. The results are shown in the table below.

Energy Comparison between Some Anti and Gauche Forms of 1,5-hexadiene

Conformer/Form	Structure	Energy (Hartrees)	Point Group
Anti1		-231.69260235	C2
Anti2		-231.69253514	Ci
Anti3		-231.68907065	C2h
Anti4		-231.69097052	C1
Gauche1		-231.68771613	C2
Gauche3		-231.69266120	C1
Gauche4		-231.69153035	C2

Anti2: https://www.ch.imperial.ac.uk/wiki/images/c/cd/KHAIMING_REACT_CI_ANTI2.LOG, Anti3: https://www.ch.imperial.ac.uk/wiki/images/3/3e/KHAIMING_REACT_ANTI3.LOG, Anti4: https://www.ch.imperial.ac.uk/wiki/images/5/5b/KHAIMING_REACT_ANTI4.LOG, Gauche1: https://www.ch.imperial.ac.uk/wiki/images/4/4e/KHAIMING_REACT_GAUCHE_TRY.LOG, Gauche3: https://www.ch.imperial.ac.uk/wiki/images/0/01/KHAIMING_REACT_GAUCHE3.LOG

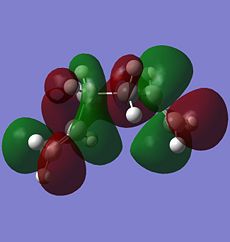
From the table, it is observed that the anti forms (anti1 and anti2) are generally more stable and have lower energies than the gauche forms (gauche1 and gauche 4) which is quite consistent with the prediction. The only exception to this is the unusual anti3 and anti4 forms which have the alkene group pointing upwards or downwards instead of the more stable pointing sideways direction (as observed in anti1 and anti2). It can be said that the more alkene groups found pointing in the axial (up/down) direction will result in more destabilisation in the anti form as the anti3 form with two axial pointing akene groups is less stable than the anti4 form which has only 1 alkene group in the axial direction. Surprisingly, one of the gauche form, gauche3, is found to have an even lower energy level than the anti forms, making it more stable than the anti forms, unlike the other gauche conformers. The reason for this can be explained from the molecular orbitals of the gauche3 form of 1,5-hexadiene. MO: https://www.ch.imperial.ac.uk/wiki/images/c/c0/KHAIMING_REACT_GAUCHE3_MO_ANALYSIS.LOG

There is considerable orbital overlap between the σ C-H bonding orbital and the π* C=C antibonding orbital due to the approximately periplanar relationship between the two orbitals. The bonding pair of electrons in the σ C-H bond is donated into the empty π* C=C antibonding orbital and this gives some stabilisation effect. In the structure of the gauche3 form, there is one possible σ_C-H→π*_C=C for each of the alkene bond, giving it a total of two stabilisations due to the σ_C-H→π*_C=C interaction. The orbital interactions are shown in the molecular orbitals below, with the σ C-H bonding orbital as MO 22 (HOMO-1) and the π* C=C antibonding orbital as MO 24 (LUMO). The two σ_C-H→π*_C=C interactions can happen due to the right phase overlap between the two orbitals (marked red for one of the double bonds and green for the other one).

Selected Molecular Orbitals of Gauche3 1,5-hexadiene

MO 22	MO 24	MO 15	MO 25

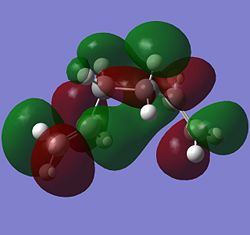Another possible orbital overlap interaction is between MO 15 and MO 25. For the empty MO 25, there seems to be some combination between the two π*_C=C orbitals causing the space between the two orbitals to have an orbital (marked green in colour). This orbital can accept electron density from one of the filled orbitals of the C-H bond (marked green in MO 15) giving rise to stability in the gauche3 form.

C_i Anti2 Conformer of 1,5-hexadiene

The energy of the anti2 conformer of 1,5-hexadiene is calculated to be -231.69253514 Hartrees, which is the same as the value given in Appendix 1. Its point group is C_i, again consistent with the one given in Appendix 1. This anti2 form is only slightly destabilised than the anti1 form by an approximated value of 0.18 kJ/mol, which means that the stability of both anti forms are essentially the same. The only difference between the two is their point groups. The anti2 conformer is then reoptimised using a higher level of theory (B3LYP/6-31G*) and its energy is now found to be more negative (-234.61170586 Hartrees) although its point group remains as C_i. Comparing this energy value with that given in Appendix 2, it is found that the calculated value is approximately the same as the one given (-234.611710 Hartrees), proving that the optimisation calculation is correct. A comparison between the optimised structures of the anti2 conformer obtained from the different levels of theory is shown in the table below. Anti2(HF/3-21G): https://www.ch.imperial.ac.uk/wiki/images/c/cd/KHAIMING_REACT_CI_ANTI2.LOG, Anti2(B3LYP/6-31G*): https://www.ch.imperial.ac.uk/wiki/images/7/7a/KHAIMING_REACT_CI_ANTI2_B3LYP.LOG

Comparison of the Optimised Structures of the Anti2 Conformer at Different Levels of Theory

Parameter	HF/3-21G	B3LYP/6-31G*
Structure	Anti2 HF/3-21G	Anti2 B3LYP/6-31G*
Energy (Hartrees)	-231.69253514	-234.61170586
Point Group	Ci	Ci
C=C Bond Length (Å)	1.32	1.33
C2-C3 & C4-C5 Bond Length (Å)	1.51	1.50
C3-C4 (Centre) Bond Length (Å)	1.55	1.55
C1C2C3 & C4C5C6 Bond Angle (°)	124.8	125.3
C2C3C4 & C3C4C5 Bond Angle (°)	111.3	112.7
C1C2-C3C4 & C3C4-C5C6 Dihedral Angle (°)	114.6	118.8
C2C3-C4C5 Dihedral Angle (°)	180.0	180.0

The energy of the anti2 form of 1,5-hexadiene is found to be different using the two levels of theory with the B3LYP/6-31G* giving a more negative energy value. However, this does not mean that the optimised structure from the B3LYP/6-31G* level of theory is more stable than the one from the HF/3-21G as different levels of theory uses different methods and basis sets in their calculations and the energies given by them cannot be compared directly for the determination of stability. Both structures still retain their C_i point group but their carbon-carbon bond lengths changes slightly. Only the centre C-C bond length is the same for both optimised structures. The bond angles between any three C atoms are slightly larger in the optimised structure using the B3LYP/6-31G* level of theory than the one for the HF/3-21G level of theory. The dihedral angle at the centre C-C bond between the two R groups (-CHCH₂) is the same for the two optimised structures, which is 180°, indicating that the four central C atoms still have the antiperiplanar conformation. However, there is a considerable difference in the dihedral angles between C₁C₂-C₃C₄ & C₃C₄-C₅C₆ with the B3LYP/6-31G* optimised structure having a much larger angle. This means that the B3LYP/6-31G* level of theory will give an anti2 structure which has the C atoms more spread out from each other. Overall, the use of two different levels of theory for the optimisation of the anti2 form of 1,5-hexadiene will give two structures which have the same point groups but the bond and dihedral angles of the optimised structure using the B3LYP/6-31G* level of theory is larger than the one using HF/3-21G.

Frequency Calculations of C_i Anti2 Conformer of 1,5-hexadiene

After obtaining an optimised structure for the anti2 conformer at the B3LYP/6-31G* level of theory, a frequency calculation is performed at the same level of theory to check that the optimised structure is in fact a minimum point and not a transition state. This can be done by comparing the energy of the optimised structure given by the optimisation and frequency calculations and looking at the vibrational frequencies of the structure. For this optimised anti2 conformer, the energy is found to be the same (-234.61170586 Hartrees) from both the optimisation and frequency calculation, and there is no imaginary or negative vibrational frequencies. This confirms that the optimised structure obtained at the B3LYP/6-31G* level of theory is indeed a minimum point which is not a transition state. Frequency Calculations: https://www.ch.imperial.ac.uk/wiki/images/0/0a/KHAIMING_REACT_CI_ANTI2_B3LYP_FREQ.LOG

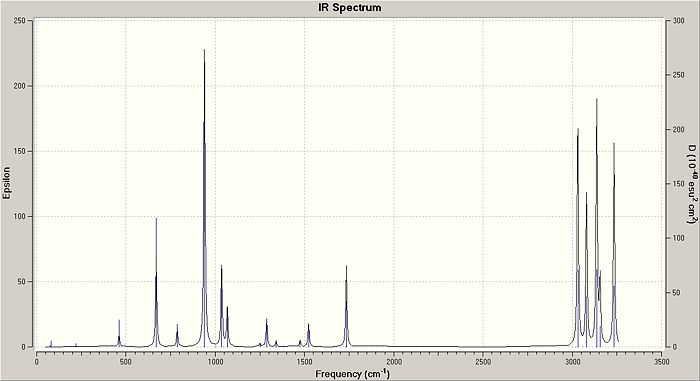
Other information obtained from the frequency calculations are the infrared spectrum and the vibrational frequencies of the anti2 form of 1,5-hexadiene, which are shown below.

Stretching Frequencies of Anti2 Conformer of 1,5-hexadiene

Vibrational Frequencies (cm-1)	Intensity	Assignment
3234	45	C-H Stretch (Alkene)
3156	15	C-H Stretch (Alkene)
3137	56	C-H Stretch (Alkene)
3080	36	C-H Stretch (Alkane)
3031	54	C-H Stretch (Alkane)
1734	18	C=C Stretch

The Gaussian output file (.log) from the frequency calculations can be opened to find out some energies of the anti2 conformer at 298.15K (Thermochemistry section) and they are listed below, together with the reference values given in the results table of Appendix 2. It is found that there is a good agreement between the calculated energy values with the one given in Appendix 2, indicating that the frequency calculations have been performed correctly. It is also noticed that the sum of the electronic and another type of energy (last four entries in the table) are more positive than the electronic energy only, suggesting that the zero-point energy, thermal energy, thermal enthalpy and free energy have a positive value.

Types of Energies of the Anti2 Conformer at 298.15K

Type of Energy	Energy Value (Hartrees)	Reference Value (Hartrees) [from Appendix 2]
Electronic Energy	-234.611706	-234.611710
Sum of Electronic and Zero-Point Energies	-234.469242	-
Sum of Electronic and Thermal Energies	-234.461887	-234.461856
Sum of Electronic and Thermal Enthalpies	-234.460943	-
Sum of Electronic and Thermal Free Energies	-234.500821	-

These energies can be recalculated at 0K by using the Freq=ReadIsotopes option in the Gaussian calculation and adding and editing some lines in the Gaussian input file (DOI:10042/to-4163 ). All these energies are found to be the same (-234.468805 Hartrees) at 0K. When the sum of the electronic and the zero-point energy is compared to the one given in Appendix 2 (-234.469203 Hartrees), a slight difference between these two values is observed, however, the diffference is considerably small. The fact that the four energies are the same at 0K is expected as there is no thermal energy in the molecule at 0K and this means that the four energies are actually the same as the sum of the electronic and zero-point energies.

Optimisation of "Chair" and "Boat" Transition Structures

Optimisation of the Chair Transition State

Firstly, the allyl fragment, CH₂CHCH₂, is optimised at the HF/3-21G level of theory before a guessed chair transition state is drawn using two of the optimised allyl fragments with a distance of 2.2Å between them. The guessed chair transition state will then be optimised at the HF/3-21G level of theory using two different methods. The two methods used and the results are described below.

Method 1: Optimisation using the Force Constant Matrix (Hessian)

The optimisation and frequency calculations are performed on the guessed chair transition state, using the options: Optimisation to a TS(Berny), Calculation of force constants = Once, and Opt=NoEigen. Opt+Freq Calculations: https://www.ch.imperial.ac.uk/wiki/images/7/78/KHAIMING_CHAIR_TS_OPT%2BFREQ.LOG

The optimised chair transition state and its energies are shown below.

Energies of the Chair Transition State

Type of Energy	Energy Value (Hartrees)	Reference Value (Hartress) [from Appendix 2]
Electronic Energy	-231.619322	-231.619322
Sum of Electronic and Zero-Point Energies	-231.466706	-231.466705
Sum of Electronic and Thermal Energies	-231.461346	-231.461346

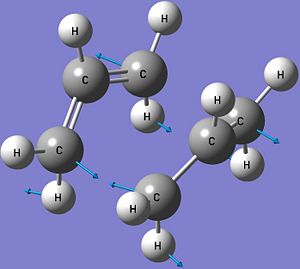
The energies given by the calculations are exactly the same as the one given in Appendix 2. This suggests that the Gaussian calculations are carried out correctly. It is also found that there is an imaginary frequency at -818 cm^-1 and this vibration is shown in the diagram below. This vibration is consistent with the Cope Rearrangement as the vibration shows that the formation of a new σ C-C bond will result in the cleavage of the σ C-C bond opposite it, together with a change in the position of the C=C bonds. As the vibrational frequency is negative, this shows that the optimised structure is a transition state and this proves that the optimised structure is in fact the chair transition state.

Method 2: Optimisation using the Frozen Coordinate Method

The guessed chair transtion state is first optimised as if it was for a minimum with the option Opt=ModRedundant and the distance between C-C bonds forming/breaking fixed at 2.2Å (https://www.ch.imperial.ac.uk/wiki/images/4/4f/KHAIMING_CHAIR_TS_MODREDUNDANT.LOG). Then, the C-C bonds in the optimised structure are unfrozen and a transition state optimisation is performed without calculating the force constants (https://www.ch.imperial.ac.uk/wiki/images/a/a1/KHAIMING_CHAIR_TS_MODREDUNDANT_OPT%2BFREQ.LOG). The second optimised structure of the chair transition state and its energies are shown below.

Energies of the Chair Transition State

Type of Energy	Energy Value (Hartrees)	Reference Value (Hartress) [from Appendix 2]
Electronic Energy	-231.619322	-231.619322
Sum of Electronic and Zero-Point Energies	-231.466699	-231.466705
Sum of Electronic and Thermal Energies	-231.461340	-231.461346

The optimised stucture of the chair transition state looks about the same as the one found using the first method. The electronic energies of the chair transtition states obtained using both methods are exactly the same while the sum of the electronic and zero-point energies and sum of the electronic and thermal energies are approximately equal to each other. The second optimised chair transition state also shows an imaginary frequency at -818 cm^-1 which corresponds to the Cope Rearrangement, just like the one from the first optimisation method. The C-C bond breaking and bond forming bond lengths in both optimised chair transition states are the same (2.02Å) with a very small difference which is below the accuracy of the bond length calculations. All these suggests that the chair transition states calculated using both methods are the same.

Optimisation of the Boat Transition State

The optimised boat transition state is calculated from the reactant and product of the Cope Rearrangement (two different C_i anti2 conformers of 1,5-hexadiene) by interpolating the two structures until the transition state is located. The atoms on both structures must be labelled correctly and some of the dihedral and bond angles are modified before a QST2 calculation at the HF/3-21G level of theory is performed to find the optimised structure of the boat transition state. The optimised boat transition state is shown below. QST2 Calculations: https://www.ch.imperial.ac.uk/wiki/images/1/1e/KHAIMING_BOAT_QST2_MODIFIED.LOG

The C-C bond breaking and bond forming bond lengths in the optimised boat transition state is 2.14Å, which is slightly longer than the bonds in the optimised chair transition state (2.02Å). The optimised boat transition state has the C_2v point group, unlike the optimised chair transition state which is not symmetrical due to the slight difference in the C-C bond breaking and bond forming bond lengths. Some of the energies of the optimised boat transition state are compared with the ones given in Appendix 2 and they are shown in the table below.

Energies of the Boat Transition State

Type of Energy	Energy Value (Hartrees)	Reference Value (Hartress) [from Appendix 2]
Electronic Energy	-231.602802	-231.602802
Sum of Electronic and Zero-Point Energies	-231.450923	-231.450929
Sum of Electronic and Thermal Energies	-231.445290	-231.445300

It is found that the calculated electronic energy of the boat transition state is the same as the one given in Appendix 2 while the other two energies are very close to each other. This means that the QST2 calculations have been done correctly and the optimised structure is a good representation of the boat transition state. There is one negative imaginary vibrational frequency at -840 cm^-1 and this vibration is shown below. The existance of the imaginary frequency confirms that the structure is a transition state, while the vibrational motion is consistent with the Cope Rearrangement. The vibration involves one σ C-C bond being formed while another σ C-C bond is broken with the double bonds in the structure changing places which is observed during a Cope Rearrangement.

IRC Method for the Chair Transition State

The Intrinisic Reaction Coordinate (IRC) method can be used to allow us to observe how the structure of the transition state changes (geometrically) until it becomes the product which is a minimum point in the potential energy surface. The IRC calculations are done at the HF/3-21G level of theory using the chk file of the optimised chair transition state obtained using the frozen coordinate method. Since the reaction coordinate is symmetrical, the IRC calculation is performed in the forward direction only. For the first IRC calculation, it is done with the option of calculating the force constants once and setting 50 points along the IRC. 1^st IRC Calculation: https://www.ch.imperial.ac.uk/wiki/images/6/60/KHAIMING_CHAIR_TS_MODREDUNDANT_OPT%2BFREQ_IRC.LOG

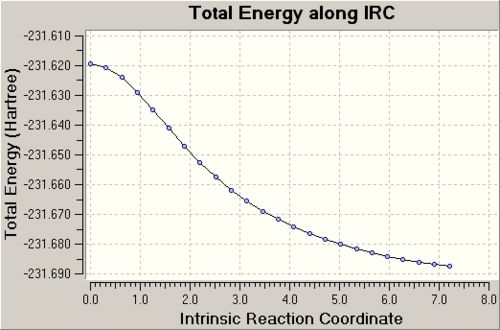
After the 1st IRC calculation, it is found that there is only 24 IRC points considered in the calculation with 24 intermediate geometries. The graph of the total energy along the the IRC path is shown below. It is observed that the IRC calculation is stopped before a geometry with the minimum energy is reached. The reason for this termination is that the gradient of the potential energy graph is assumed to be small enough to be considered as a minimum point (gradient reaches a threshold value) after a certain point. In fact, the real minimum of the graph has not been reached. This can be proven by considering the energy of the 24^th intermediate structure which is -231.68753 Hartrees to the energy of the possible end product of the Cope Rearrangement which is a conformer of 1,5-hexadiene. The least stable form of 1,5-hexadiene is the gauche1 form and this form has the highest energy (-231.68772 Hartrees) among all the other conformers but this is still lower than the one for the 24^th intermediate structure. Thus, it can be said that the 1^st IRC calculation has failed to reached the real minimum point of the potential energy graph where the product is.

The changes in the geometry of the chair transition state are shown in the table below for certain points in the IRC calculation path.

Changes in Geometry of the Chair Transition State at Some Points of the IRC Path

1st Point	5th Point	10th Point	15th Point	20th Point	24th Point

To get the real minimum of the potential graph where the structure of the product can be obtained, three different methods can be used. These methods are described below, together with the results obtained from the application of the methods. The three methods are:

1. Restarting the IRC with more points along the IRC

The IRC calculations are performed on the optimised chair transition state structure but for this one, the number of points on the IRC is increased from 50 to 150. As expected, the IRC calculation is terminated after the 24^th point which is the same as the one for the 1^st IRC calculation. The failure of this method is related to the limitation of the IRC calculation (the options used) where the gradient of the potential energy graph is assumed to be small enough to be a minimum point but in reality, that point is not the minimum point on the potential energy graph. The structure and energy of the 24^th intermediate structure is the same as the 1^st IRC calculation, suggestion that the same IRC paths are taken and terminated at the same point. 2^nd IRC (150 points): https://www.ch.imperial.ac.uk/wiki/images/b/bb/KHAIMING_CHAIR_TS_MODREDUNDANT_OPT%2BFREQ_IRC_%28II%29.LOG

2. Normal minimisation on the 24^th intermediate structure of the 1^st IRC calculation

The second method involves the use of the last point of the 1^st IRC calculation (24^th intermediate) in the optimisation to a minimum calculation. The optimised product structure is shown below. It is found that the calculated electronic energy is given as -231.69166701 Hartrees, which corresponds to the energy of the gauche2 conformer of 1,5-hexadiene. In fact, the optimised structure of the product looks like the gauche2 form and its point group is also the same (C₂). Hence, it can be concluded that the optimised structure of the product of the Cope Rearrangement obtained using this method is the gauche2 form of 1,5-hexadiene. Optimisation: https://www.ch.imperial.ac.uk/wiki/images/f/fe/KHAIMING_CHAIR_TS_MODREDUNDANT_OPT%2BFREQ_IRC_%28I%29.LOG

Optimised Product Structure (Method 1)

3. Restarting the IRC using the option of calculating the force constants at every step

The IRC calculation is performed again on the optimised chair transition state, this time using the options: calculating the IRC in the forward direction only, calculating the force constants at every step along the IRC and setting the number of points along the IRC to 50. The IRC calculation is terminated after the 47^th intermediate structure and the change of the potential energy graph along the IRC is shown below. 2^nd IRC (Always calculate force constants): https://www.ch.imperial.ac.uk/wiki/images/5/50/KHAIMING_CHAIR_TS_MODREDUNDANT_OPT%2BFREQ_IRC_%28III%29.LOG

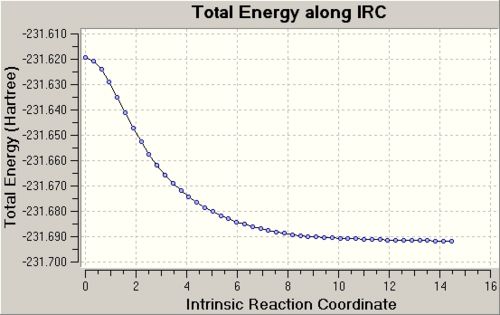
This time, the IRC calculation is able to find the minimum point on the potential energy graph which means that the last point or structure of the IRC path is in fact the optimised structure of the product of the Cope Rearrangement. The electronic energy of the product is calculated to be -231.69166432 Hartrees which is very close to the energy of the gauche2 form of 1,5-hexadiene given in Appendix 1. Inspection of the optimised structure of the product shows that the product of the reaction is in fact the Gauche2 conformer of 1,5-hexadiene, and this is consistent with the result obtained using the second method (described above). This means that the chair transition state will lead to the product with the gauche2 form in the Cope Rearrangement of 1,5-hexadiene. The optimised structure of the product and also the structures of some points along the IRC path are shown below. It is observed that one new σ C-C bond is formed while the other two C ends move away from each other as the transition state changes into the product.

Changes in Geometry of the Chair Transition State at Some Points of the IRC Path

1st Point	8th Point	16th Point	24th Point	32th Point	40th Point	47th Point

IRC Method for the Boat Transition State

The IRC calculation is performed on the optimised boat transition state using the following options: calculating the IRC in the forward direction only, calculating the force constants at every step along the IRC and setting the number of points along the IRC to 50. Boat transition state IRC: https://www.ch.imperial.ac.uk/wiki/images/e/e3/KHAIMING_BOAT_QST2_MODIFIED_IRC.LOG

At the end of the IRC calculation, it is found that there are 47 points along the IRC path and the last structure (47^th intermediate) corresponds to the minimum point on the potential energy graph. This means that the 47^th intermediate structure is in fact the optimised structure of the product of the Cope Rearrangement of 1,5-hexadiene via the boat transition state. The changes in the potential energy of the structure along the IRC path is shown below, together with the structures of some intermediates along the IRC path. As the transition state changes into the product, one new σ C-C bond is formed while the other ends of the 6-membered chain moves away from each other.

Changes in Geometry of the Boat Transition State at Some Points of the IRC Path

1st Point	8th Point	16th Point	24th Point	32th Point	40th Point	47th Point

The energy of the optimised product is calculated to be -231.68302517 Hartrees and this is higher than the energies of all the possible conformers of 1,5-hexadiene given in Appendix 1. The reason for this is that the optimised structure of the product does not fall into any of the types of anti and gauche conformers given in Appendix 1. The optimised structure of the product, which is shown below, has the two R groups (-CHCH₂) in a periplanar relationship when viewed along the central C₃-C₄ bond. The closer distance between the two periplanar R groups will result in considerable steric repulsion between the two groups, which raises the energy of the product. However, this product structure of 1,5-hexadiene is not expected as it is assumed that the product state would exist in a more stable conformer state.

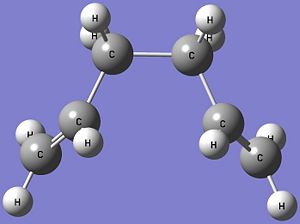
Optimised Product Structure (via Boat TS)

Reoptimisation of the Chair and Boat Transition State Structures

After obtaining the optimised structures of the chair and boat transition states at the HF/3-21G level of theory, these transition states structures are reoptimised using a higher level of theory, B3LYP/6-31G*. Frequency calculations at the B3LYP/6-31G* level are then performed on the optimised structures of the chair and boat transition states. Chair transition state optimisation: DOI:10042/to-4164 , chair transition state frequency: DOI:10042/to-4166 , boat transition state optimisation: DOI:10042/to-4165 , boat transition state frequency: DOI:10042/to-4167 .

The optimised structures of the chair and boat transition states at the B3LYP/6-31G* level of theory, and the table showing the comparison between the optimised structures of the transition states obtained at the HF/3-21G and B3LYP/6-31G* levels of theory are shown below. Both the optimised chair and boat transition states have an imaginary frequency each, confirming that the structures are transition states and the vibrations are also consistent with the Cope Rearrangement.

Optimised Chair Transition State (B3LYP/6-31G*)

Optimised Boat Transition State (B3LYP/6-31G*)

Comparison Between the Optimised Chair Transition States

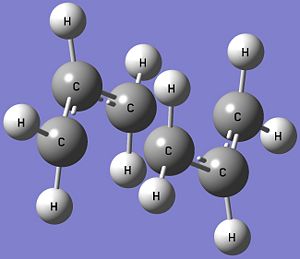
Parameter	HF/3-21G	B3LYP/6-31G*
Electronic Energy (Hartrees)	-231.619322	-234.556983
Sum of Electronic and Zero-Point Energies (Hartrees)	-231.466699	-234.414927
Sum of Electronic and Thermal Energies (Hartrees)	-231.461340	-234.409008
Imaginary Frequency (cm-1)	-818	-565
Point Group	C1	C1
C-C Bond Breaking/Forming Bond Length (Å)	2.02	1.97

Comparison Between the Optimised Boat Transition States

Parameter	HF/3-21G	B3LYP/6-31G*
Electronic Energy (Hartrees)	-231.602802	-234.543093
Sum of Electronic and Zero-Point Energies (Hartrees)	-231.450923	-234.402344
Sum of Electronic and Thermal Energies (Hartrees)	-231.445290	-234.396008
Imaginary Frequency (cm-1)	-840	-530
Point Group	C2v	C2v
C-C Bond Breaking/Forming Bond Length (Å)	2.14	2.21

It is observed that the structures of the chair transition state obtained from the two levels of theory are about the same, with the bond length of the C-C bond being broken/formed slightly longer in the structure obtained using the HF/3-21G level of theory. For the boat transition state, the two optimised structures from the two levels of theory are also about the same with the difference being the bond length of the C-C bond being broken/formed is slightly longer in the structure calculated at the B3LYP/6-31G* level of theory. The point groups for the chair and boat transition states remain the same irrespective of the level of theory used for the optimisation. The imaginary vibrational frequencies for both transition states are different at different levels of theory as the methods used to calculate them are different, but their vibrations are consistent with the Cope Rearrangement of 1,5-hexadiene.

The energies of the boat and chair transition states calculated using the B3LYP/6-31G* level of theory are very different from that given by the HF/3-21G and this is expected as the different methods used for the calculations and optimisations use different considerations and this will definitely affect the energies. However, the boat transition state is still found to have a higher energy level (less stable) for both levels of theory, and this proves that the boat transition state is always less stable than the chair transition state. Comparing the calculated energies from the HF/3-21G and B3LYP/6-31G* levels of theory with those listed in Appendix 2, it is found that there is a very good match for all the energies, suggesting that both calculations have been performed correctly.

Calculation of the Activation Energies

The activation energies for the Cope Rearrangement of 1,5-hexadiene via the chair and boat transition states can be calculated from the difference in energies of the reactant (assumed to be the anti2 conformer) and the transition states. These activation energies for the Cope Rearrangement can be calculated at different temperatures by comparing the sum of electronic and zero-point energies (0 K) and the sum of electronic and thermal energies (above 0 K). The B3LYP/6-31G* level of theory is used to optimise and calculate the energies of the reactant and transition states at different temperatures. The table below lists the energies of the anti2 reactant, chair and boat transition states at different temperatures calculated at the B3LYP/6-31G* level of theory. Anti2(0 K): DOI:10042/to-4163 , Anti2(298.15 K): https://www.ch.imperial.ac.uk/wiki/images/0/0a/KHAIMING_REACT_CI_ANTI2_B3LYP_FREQ.LOG, Anti2(398.15 K): DOI:10042/to-4182 , Chair T.S.(0 K): DOI:10042/to-4168 , Chair T.S.(298.15 K): DOI:10042/to-4166 , Chair T.S.(398.15 K): DOI:10042/to-4173 , Boat T.S.(0 K): DOI:10042/to-4169 , Boat T.S.(298.15 K): DOI:10042/to-4167 , Boat T.S.(398.15 K): DOI:10042/to-4174 .

Energies of the Anti2 Form of 1,5-hexadiene, Chair and Boat Transition States

Structure	Sum of Electronic and Zero-Point Energies - 0 K (Hartrees)	Sum of Electronic and Thermal Energies - 298.15 K (Hartrees)	Sum of Electronic and Thermal Energies - 398.15 K (Hartrees)
Reactant (Anti2)	-234.469242	-234.461887	-234.456781
Chair Transition State	-234.414927	-234.409008	-234.404195
Boat Transition State	-234.402344	-234.396008	-234.391011

The activation energies of the Cope Rearrangement of 1,5-hexadiene via the boat and chair transition states are then calculated and the results at different temperatures are given in the table below.

Activation Energies of the Cope Rearrangement via Chair and Boat Transition States at Different Temperatures

Activation Energy	0 K (kcal/mol)	298.15 K (kcal/mol)	398.15 K (kcal/mol)	Experimental Value at 0 K (kcal/mol)
ΔEA (chair)	34.08	33.18	33.00	33.5 ± 0.5
ΔEA (boat)	41.98	41.34	41.27	44.7 ± 2.0

It is found that the activation energy via the boat transition state for the Cope Rearrangement is always higher than the activation energy via the chair transition state. This means that less energy is required to convert the anti2 reactant to the chair transition state than the boat transition state and hence, the Cope Rearrangement of 1,5-hexadiene proceeds through the chair transition state due to the lower activation energy. The calculated activation energies at 0 K via both transition states are very close to the experimental range, and this means that the B3LYP/6-31G* level of theory can be used to get a very good approximation of the activation energies for the Cope Rearrangement. For ΔE_A (chair), it is within the experimental range whereas the ΔE_A (boat) lies very close to the experimental range. It is also observed that both activation energies (via boat and chair transition states) decreases slightly with the increase of temperature. This is expected as less energy is required to overcome the activation energy at higher temperatures due to the thermal energy present in the structure of the reactant.

The Diels Alder Cycloaddition

The Diels Alder reaction is a type of pericyclic reaction where the π orbitals of the dienophile interact with the π orbitals of the diene to form two new σ bonds between the diene and dienophile. The product of this reaction is a new cylic/ring molecule which can also include a fused ring system, depending on the type of diene and dienophile used in the reaction. Three Diels Alder cycloadditions are studied in this computational experiment, one involving cis-butadiene and ethene, and another two between substituted dienes and dienophiles.

Diels Alder Reaction Between Cis-Butadiene and Ethene

Optimisation and Molecular Orbitals of Cis-Butadiene and Ethene

Cis-butadiene and ethene can react in a Diels Alder reaction to give the cyclic product, cyclohexene. This Diels Alder reaction is a [4+2] cycloaddition as it involves four π electrons on the cis-butadiene and two π electrons on the ethene. The molecular orbitals of the reactants can be viewed and examined after the optimisation of the reactants using the AM1 semi-empirical molecular orbital method. Cis-butadiene Optimisation: https://www.ch.imperial.ac.uk/wiki/images/4/40/KHAIMING_CIS_BUTADIENE_OPT.LOG, Ethene Optimisation: https://www.ch.imperial.ac.uk/wiki/images/c/ca/KHAIMING_ETHENE_OPT.LOG

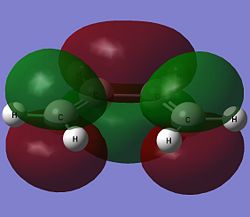
The highest occupied molecular orbital (HOMO) and the lowest unoccupied molecular orbital (LUMO) of both cis-butadiene and ethene are shown below.

HOMO and LUMO of Cis-Butadiene and Ethene

Reactant	HOMO	LUMO
Cis-Butadiene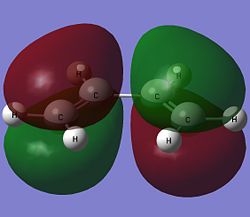
Ethene

The HOMO of cis-butadiene is anti-symmetric with respect to the reflection plane while the LUMO is symmetric. For ethene, the symmetry of the molecular orbitals are the opposite of that for cis-butadiene. The HOMO of ethene is symmetric while the LUMO is anti-symmetric with respect to the reflection plane. As orbitals can only interact when they have the same symmetry, this means that only the HOMO of cis-butadiene can interact with the LUMO of ethene and only the LUMO of cis-butadiene can overlap with the HOMO of ethene.

Transition State of Cis-Butadiene+Ethene

The transition state of this Diels Alder reaction is believed to have an envelope type structure as this helps to maximise the overlap between the π orbitals of cis-butadiene and ethene. The guessed transition state is formed from a bicyclo system with one of the -CH₂CH₂- fragment removed. Two of the σ C-C bonds are removed to form the two cis-butadiene and ethene fragments with the interfragment distance set at 2.20Å. The guessed transition state structure is then optimised using the AMI method. The optimisation and frequency calculations are performed using the option: minimisation to a TS (Berny), calculation of the force constants once and Opt=NoEigen. Optimisation and Frequency Calculations of Transition State: https://www.ch.imperial.ac.uk/wiki/images/f/f6/KHAIMING_TS_METHOD1_OPT%2BFREQ.LOG

The optimised structure of the transition state from the AM1 method is then reoptimised at a higher level of theory. The second optimisation and frequency calculations are performed at the B3LYP/6-31G* level of theory and the optimised structure obtained from this optimisation is compared with the one obtained using the AM1 method. Optimisation (B3LYP/6-31G*): DOI:10042/to-4179 , Frequency Calculations (B3LYP/6-31G*): DOI:10042/to-4180 .

Comparison of the Optimised Structures of the Transition State Obtained at Different Levels of Theory

Parameter	AM1	B3LYP/6-31G*
Structure
Energy (Hartrees)	0.11165478	-234.54389655
C-C bond formed/broken Bond Length (Å)	2.12	2.27
C=C Bond Length (Å)	1.38	1.38 (1.39 for ethene)
C-C (partially C=C) Bond Length (Å)	1.40	1.41
Imaginary Frequency (cm-1)	-956	-525

Comparing the two optimised structures of the transition state, it is observed that both of them are about the same with the ethene fragment approaching the cis-butadiene from the top face. The bond lengths of the partly formed σ C-C bonds are different for the two structures with the one obtained at the B3LYP/6-31G* level of theory having a much longer C-C bond length. The other C=C and C-C bond lengths in the transition state structures are about the same. The calculated energy of the two structures are different and this is expected as they are calculated using different methods and they cannot be used to compare the relative stability of the transition states. The imaginary frequencies are negative for both structures and this confirms that the optimised structures are indeed transition states. They are different for the two transition state structures just like the calculated energies, and this is again expected as the method used to calculate them is different. However, both the vibrational frequencies are consistent with the Diels Alder reaction. The vibration corresponding to the negative frequency is shown below.

The negative frequency vibration is the one that corresponds to the reaction path at the transition state. It is observed that during this vibration, the two new σ C-C bonds are formed at the same time, while the other C-C bonds in the structure change to either a C-C single or C=C double bonds. As the two new C-C bonds are formed at the same time, the formation of the two bonds are synchronous and not a stepwise formation of a single C-C bond. The lowest positive vibrational frequency is at 136 cm^-1 (B3LYP/6-31G* level) and this is much larger than the imaginary negative vibrational frequency. The vibration motion at the lowest positive vibrational frequency is shown below. Its motion seems to be the in-plane rocking of the two fragments with the ethene fragment rocking more strongly than the cis-butadiene fragment. This vibration is very different from that of the negative frequency.

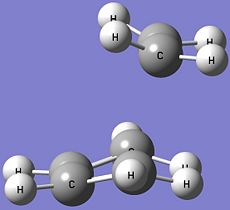
The optimised structure of the transition state at the B3LYP/6-31G* level of theory is shown below.

Side View of Transition State

Optimised Transition State

It is observed that there is a reflection plane across the centre of the two fragments of the transition state. The bond lengths of the two partly formed σ bonds are about the same, 2.27Å. A typical sp³ C-C bond length is about 1.54Å while a sp² C-C bond length is approximately 1.34Å . The C-C bond length of the partly formed σ C-C bonds in the transition state is larger than the bond lengths of a sp³ and sp² C-C bond, but smaller than twice the Van der Waals radius of the C atom, which is about 1.70Å . This means that the C atoms on the two fragments in the transition state are close together but not close enough to form any real σ C-C bonds, hence, the bond is only partially formed. The partially formed C-C bond is much longer and weaker than a formal C-C single bond.

Molecular Orbitals of Transition State of Cis-Butadiene+Ethene

The molecular orbitals of the optimised transition state are viewed using the fck file from the AM1 calculations. The HOMO and LUMO of the transition state and their symmetries are reported in the table below.

HOMO and LUMO of Transition State

HOMO	LUMO
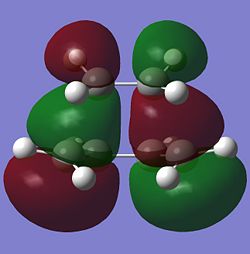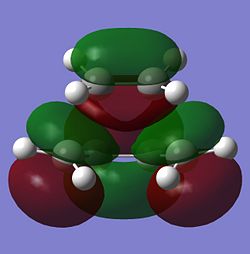
Anti-symmetric	Symmetric

The HOMO at the transition state is very clearly anti-symmetric with respect to the plane. Since the anti-symmetric HOMO of the transition state can only come from the overlap between two anti-symmetric molecular orbitals from cis-butadiene and ethene, it can be concluded that the HOMO of cis-butadiene and the LUMO of ethene have been used to form the HOMO of the transition state. Looking again at the HOMO of the transition state (shown below), it can be seen that there is a large orbital overlap density between the cis-butadiene and ethene fragments and the phases of these orbitals confirm that the HOMO of the transition state must be formed using the HOMO of cis-butadiene and LUMO of ethene. This Diels Alder reaction is allowed because the HOMO of cis-butadiene is able to interact with the LUMO of ethene due to the similar symmetry of the two molecular orbitals and the significant overlap density between the two molecular orbitals.

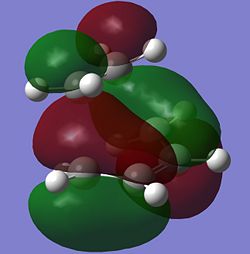
IRC Path for Transition State of Cis-Butadiene+Ethene

The reaction path from the transition state of cis-butadiene+ethene to the cyclohexene product can be studied using the IRC method. The IRC calculation is performed on the optimised structure of the transition state obtained using the AM1 method with the following options: computing the reaction coordinate in the forward direction only, calculating the force constants at every point of the IRC and setting the maximum number of points along the IRC to 100. IRC calculation: DOI:10042/to-4178 .

From the results given by the IRC calculations, it is found that there is 28 points in the IRC path before a structure for the product cyclohexene is found. The change in the potential energy of the intermediate structures along the IRC path is shown below, together with a table showing the structures of some intermediates found along the IRC path. The last point on the IRC path (28^th structure) is the optimised structure of the product as a minimum point has been found on the potential energy graph. To get to the product, the transition state will have the two cis-butadiene and ethene fragments come closer together to form the new σ C-C bonds while adjusting the other C-C bond lengths in the structure. After forming the new C-C bonds, the bond lengths and bond angles in the cyclohexene ring will then be adjusted until a minimum point is found.

Changes in Geometry of the Transition State Cis-Butadiene+Ethene at Some Points of the IRC Path

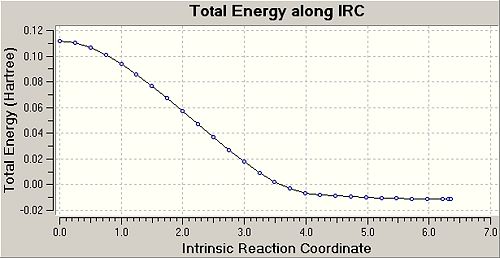
1st Point	7th Point	14th Point	21st Point	28th Point

The optimised structure of the cyclohexene product given by the IRC calculation is shown below.

Optimised Cyclohexene Product

Diels Alder Reaction Between Cyclohexa-1,3-diene and Maleic Anhydride

The Diels Alder reaction between cyclohexa-1,3-diene 1 and maleic anhydride 2 can give two possible products, the exo form 3 or the endo form 4. Experimentally, it has been shown that the endo 4 form is the major product and the reaction is supposed to be under kinetic control. This means that the activation energy for the formation of the endo 4 product is smaller and the endo transition state should be lower in energy while the exo transition state is higher in energy. This will be investigated in this part of the computational experiment.

Optimisation and Structure of the Exo and Endo Transition States

The guessed exo and endo transition states are first formed by removing the σ C-C bonds between the maleic anhydride group and the cyclohexene in the exo 3 and endo 4 products, and setting the distance between the two fragments to 2.2Å. These guessed transition states are then optimised at the AM1 level of theory using the same options as the one listed in the Transition State of Cis-butadiene+Ethene section. Exo transition state Optimisation (AM1): DOI:10042/to-4176 , Endo transition state Optimisation (AM1): DOI:10042/to-4175 . The optimised structures of the exo and endo transition states are shown below, together with a table comparing certain features of the optimised structures.

Comparison of the Exo and Endo Transition States at AM1 Level of Theory

Parameter	Exo Transition State	Endo Transition State
Structure	Optimised Exo TS	Optimised Endo TS
Energy (Hartrees)	-0.05041971	-0.05150475
Imaginary Frequency (cm-1)	-812	-807
Bond Length of Partly Formed σ C-C (Å)	2.17	2.16
C-C Through Space Distance (Å)	2.94	2.89

Bond Lengths in Exo Transition State

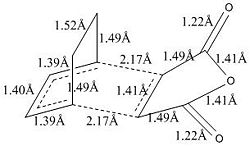
From the optimisation calculation results, it is found that the energy of the endo transition state is lower (more negative) than the energy of the exo transition state. This means that the endo transition state is more stable than the exo transition state, and the activation energy for the formation of the endo 4 product would be lower since the energy level of the reactants are the same but the endo transition state has lower energy than the exo transition state. Both the endo and exo transition states show an imaginary frequency each, with the frequency being more negative for the exo transition state than the endo transition state. The vibrations corresponding to these negative imaginary frequencies are consistent with the Diels Alder reaction and the two new σ C-C bonds are observed to have formed at the same time (concerted reaction).

Bond Lengths in Endo Transition State

The C-C through space distance listed in the table above refers to the distance between the -(C=O)-O-(C=O)- fragment of the maleic anhydride and the C atoms of the “opposite” -CH₂-CH₂- for the exo and the “opposite” -CH=CH- for the endo transition states. It is found that the C-C through distance is smaller in the endo transition state than the exo transition state. This means that the -(C=O)-O-(C=O)- fragment of the maleic anhydride lies closer to the “opposite” -CH=CH- in the endo transition state than it is to the “opposite” -CH₂-CH₂- in the exo transition state. The bond length of the partly formed σ C-C bond is found to be slightly longer in the exo transition state than the endo transition state, but their difference is very small (0.01Å). The bond lengths in the optimised structures of the endo and exo transition states are shown on the right. Besides the difference in the bond length of the partially formed C-C bond and the through space distance, the other bonds have the same bond lengths in both the endo and exo transition states.

Comparing the structures of the exo and endo transition states, it is found that the exo form is slightly more strained than the endo form. The exo form could be more strained because the maleic anhydride group is forced to point upwards towards the 'bridging' -CH₂CH₂ fragment, which is not favourable. Although the -(C=O)-O-(C=O)- fragment of the maleic anhydride is closer to the “opposite” -CH=CH- in the endo transition state, there is only two H atoms on the alkene and they are not pointing towards the -(C=O)-O-(C=O)- fragment of the maleic anhydride. This causes less repulsion between the two fragments and the energy of the endo transition state is lower. For the exo transition state, although the distance between the -(C=O)-O-(C=O)- fragment of the maleic anhydride and the C atoms of the “opposite” -CH₂-CH₂- is larger, there is two H atoms on the -CH₂-CH₂- fragment that are directly pointing to the -(C=O)-O-(C=O)- fragment. This causes considerable steric repulsion in the exo form, resulting in the higher energy of the exo form. Also, the bond angles between the C atoms of the partially formed σ C-C bond and the -(C=O)-O-(C=O)- group and the -CH₂-CH₂- group are smaller in the exo transition state (92.8° and 99.6°) than in the endo transition state (96.7° and 100.0°). This shows that the exo form is more strained than the endo form.

Molecular Orbitals of the Exo and Endo Transition States

The molecular orbitals of the exo and endo transition states can be generated from the chk files obtained from the AM1 optimisation and frequency calculations. The HOMO and HOMO-1 of both the exo and endo transition states are shown in the table below.

HOMO and HOMO-1 of the Exo and Endo Transition States

Molecular Orbital	Exo Transition State	Endo Transition State
HOMO
HOMO-1

The HOMO of both transition states are anti-symmetric with respect to the reflection plane. It is observed that there is a large orbital lobe in the space between the cyclohexa-1,3-diene fragment and the maleic anhydride fragment, and this represents the orbital overlap between the HOMO of the diene and the LUMO of maleic anhydride. In fact, the large lobe is skewed to one side with the larger part of the lobe being the position where the new σ C-C bonds are formed.

On the other hand, the HOMO-1 of both transition states are symmetrical with respect to the reflection plane. For the exo transition state, there is no secondary orbital overlap between the filled p orbitals of the O atoms from the -(C=O)-O-(C=O)- fragment and the -CH₂CH₂- fragment opposite to it as there is a nodal plane between the two fragments. There is also no orbitals present on the -CH₂CH₂ fragment to accept the electron density from the p orbtials of the O atoms in the HOMO-1 of the exo transition state. The situation is different for the HOMO-1 of the endo transition state. Secondary orbital overlap is possible between the filled p orbitals on the O atoms from the -(C=O)-O-(C=O)- fragment and the -CH=CH- fragment opposite to it due to the absence of a nodal plane between these two fragments. The orbital lobes on the O atoms are in the same phase as the orbitals on the -CH=CH- fragment, and this results in a possible orbital overlap between the two fragments. This secondary orbital overlap would result in the stabilisation of the endo transition state but the stabilisation effect is expected to be small due to the large distance between the two interacting orbitals which weakens the secondary orbital overlap. Hence, the secondary orbital overlap plays only a small part in stabilising the endo transition state.

Overall, no secondary orbital overlap effect is observed in the exo transition state but there is a considerable amount of steric repulsion present in the structure due to the -(C=O)-O-(C=O)- and -CH₂CH₂- fragments. All these destabilises the exo transition state, causing it to have higher energy. For the endo transition state, the absence of steric repulsion is more important in stabilising the structure of the endo form than the stabilisation from the the secondary orbital overlap (negligible effect). The absence of steric repulsion stabilises the endo transition state, hence, its energy is lower.

Reoptimisation of the Exo and Endo Transition States and Comparisons

The exo and endo transition states from the AM1 calculations are reoptimised at the B3LYP/6-31G* level of theory using the same options as the one used in the AM1 calculations. The structures and some properties of the newly optimised exo and endo transition states are given in the table below. Exo - Optimisation and Frequency Calculations: DOI:10042/to-4192 , Endo - Optimisation and Frequency Calculations: DOI:10042/to-4191 .

Exo and Endo Transition States at B3LYP/6-31G* Level of Theory

Parameter	Exo Transition State	Endo Transition State
Structure
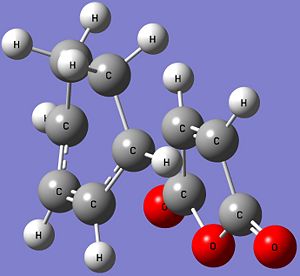
Energy (Hartrees)	-612.67931095	-612.68339703
Imaginary Frequency (cm-1)	-448	-446
Bond Length of Partially Formed σ C-C (Å)	2.29	2.27
C-C Through Space Distance (Å)	3.03	2.99

The endo transition state is found to have a lower energy level than the exo transition state, which is consistent with the results obtained using the AM1 method. The difference in energy between the two transition states is calculated to be approximately 2.56 kcal/mol, hence, it can be said that the endo form is 2.56 kcal/mol lower in energy than the exo form. Since the endo transition state is more stable, its activation energy will be lower, and the endo product will be formed faster and hence, it is the kinetic product. The imaginary frequencies calculated for both transition states are consistent with the Diels Alder reaction, and their negative values confirm that the optimised structures must be a transition state. Just like the trend seen in the AM1 calculations, the imaginary frequency is more negative for the exo transition state than the endo transition state.

The bond length of the partially formed σ C-C bond and the C-C through space distance are considerably longer in both the optimised structures of the transition states at the B3LYP/6-31G* level of theory than that at the AM1 level of theory. However, the same trend is observed when these bond length and distance are compared between the exo and endo forms at different levels of theory. The bond length of the partially formed σ C-C bond is longer in the exo form than in the endo form. The C-C through space distance is also longer in the exo form. This suggests that the structures of the transition states are more or less the same when calculated at different levels of theory, with the only difference being the absolute values of some bond lengths and angles but the general trend (larger for one transition state than the other) will remain the same.

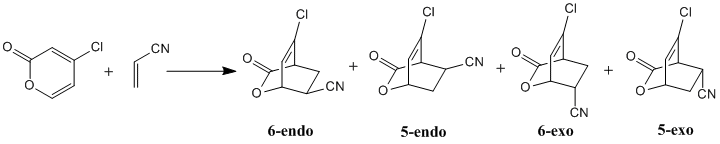
Diels Alder Reaction Between 4-Chloro-2(H)-Pyran-2-one and Acrylonitrile

The reaction shown above is the Diels Alder reaction between 4-chloro-2(H)-pyran-2-one (diene) and acrylonitrile (dienophile) where four possible products can be formed in the reaction. The four possible products are the 6-endo, 5-endo, 6-exo and 5-exo cycloadducts and the percentage yield of the products are reported to be 58%, 25%, 17% and 0% respectively . Computational calculations are performed to rationalise the distribution of yields of the products and to compare the results of the computational method reported in the literature. The use of a lower level of theory (HF/3-21G) is also examined to see whether it is good enough to explain the experimental results.

Optimisation and Structures of Transition States at B3LYP/6-31G* Level of Theory

The structures of the four transition states are guessed by removing the two new σ C-C bonds formed in the Diels Alder reaction from the structures of the four products and setting the distance between the two fragments at 2.2Å. These guessed transition states are then sent for the optimisation and frequency calculations at the AM1 level of theory. The optimised transition state structures will then be reoptimised and their frequencies calculated at the B3LYP/6-31G* level of theory before any analysis is made. 6-endo (AM1): DOI:10042/to-4187 , 5-endo (AM1): DOI:10042/to-4188 , 6-exo (AM1): DOI:10042/to-4189 , 5-exo (AM1): DOI:10042/to-4190 ; 6-endo (B3LYP/6-31G*): DOI:10042/to-4193 , 5-endo (B3LYP/6-31G*): DOI:10042/to-4194 , 6-exo (B3LYP/6-31G*): DOI:10042/to-4195 , 5-exo (B3LYP/6-31G*): DOI:10042/to-4196 .

The optimised structures, energies and imaginary frequencies of the four transition states at the B3LYP/6-31G* level are given in the table below.

Comparison Between the Four Transition States at the B3LYP/6-31G* Level

Parameter	6-endo	5-endo	6-exo	5-exo
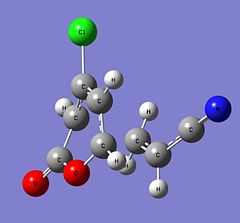
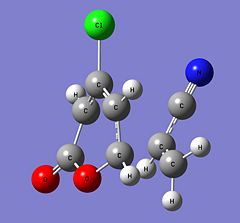
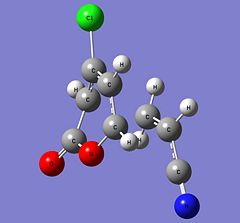
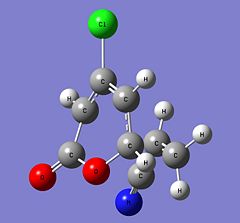
Structure	5-endo TS	5-endo TS	6-exo TS	5-exo TS
Energy (Hartrees)	-973.75516028	-973.75282472	-973.75236783	-973.75025932
Imaginary Frequency (cm-1)	-515	-521	-511	-517

All four transition states have a negative vibrational frequency each, confirming that the optimised structures are really transition states. The vibrations at the imaginary frequency are examined and they are found to be consistent with the motions of bonds during this Diels Alder reaction. The transition state of the 5-endo form has the most negative imaginary frequency, followed by the 5-exo form, 6-endo form and 6-exo form. It appears that the imaginary vibrational frequency is more negative when the -CN group is on the 5 position of the ring and not on the 6 position. The endo form of the transition state also seems to have a more negative imaginary frequency than the exo form.

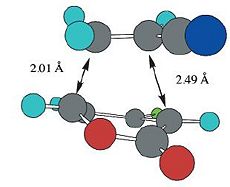
The bond lengths of the two partially formed σ C-C bonds from the optimisation at B3LYP/6-31G* are shown below and they are compared to the reported computational results, also calculated at the B3LYP/6-31G* level of theory .

Comparison of the Bond Lengths of the Partially Formed σ C-C Bonds

	6-endo	5-endo	6-exo	5-exo
Calculated Values (B3LYP/6-31G*)
Reported Values (B3LYP/6-31G*)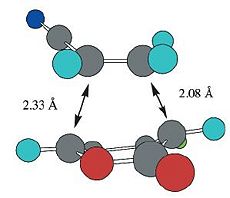

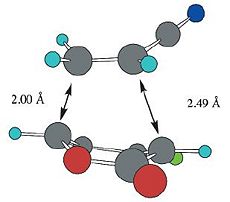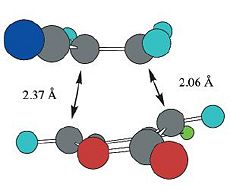From the table above, it is found that the calculated bond lengths of the partially formed σ C-C bonds are the same (some only has a difference of 0.1Å) as the ones reported in the literature. This indicates that the optimisation and frequency calculations of the transition states done in this computational experiment are consistent with the ones reported in the literature. This also means that the optimised structures of the four transition states are about the same as those in the literature, which is expected as the calculations are performed at the same level of theory.

Comparing the energies of the four transition states, the 6-endo form is found to have the lowest (most negative) energy while the 5-exo form is the one with the highest energy. As the 6-endo has the lowest energy, this transition state is the most stable form of the transition state and the stabilities of the other forms are compared to this by computing their relative energy differences. This means that the energy level of the 6-endo transition state is taken as the energy zero. The relative energy levels of the four forms of transition states are given in the following table and these values are compared to literature values .

Relative Energy Levels of the Four Forms of Transition States And The Percentage Yields

Configuration	Relative Energy Levels, ΔHrel (kcal/mol)	Literature Values (kcal/mol)	Reported Percentage Yields
6-endo	0.000	0.000	58%
5-endo	1.466	1.744	25%
6-exo	1.752	1.747	17%
5-exo	3.075	3.085	0%

The calculated relative energy levels are about the same as the ones reported in literature. The only difference is the calculated relative energy level of the 5-endo form, which is found to be smaller than the one reported in the literature, although this difference is not very big. As the 6-endo transition state is the most stable, the activation energy for the reaction producing the 6-endo product will be lower, causing the reaction to take place faster. Hence, in a kinetically-controlled reaction, the 6-endo product will be the major product and this explains the high percentage yield of the 6-endo product compared to the other possible products. The 5-exo transition state has the highest energy relative to the most stable form, and this indicates that the 5-exo form is the most disfavoured cycloadduct of the reaction. Hence, the 5-exo product is only formed in trace amounts, causing its percentage yield to be approximately 0%. The percentage yields of the 5-endo and 6-exo products are about the same as their transition states are destabilised by about the same amount relative to the 6-endo transition state. As their energy levels are between that of the 6-endo and 5-exo forms, the 5-endo and 6-exo transition states are more stable than the 5-exo form but less stable than the 6-endo form. This explains their percentage yields which are between that of the 6-endo and 5-exo products. In fact, the percentage yield of the 5-endo product is slightly higher than that of the 6-exo product as the 5-endo transition state is slightly more stabilised than the 6-exo transition state as shown by the results of this computational experiment.

In conclusion, the results of the B3LYP/6-31G* calculations done in this computational experiment support the results given in the literature and this can be used to explain the percentage yields of the Diels Alder reaction between 4-chloro-2(H)-pyran-2-one and acrylonitrile reasonably well. The only down side of this is that the calculations may take a long time due to the usage of a high level of theory (B3LYP/6-31G*). It is now investigated whether a lower level of theory (HF/3-21G), which gives faster calculations, is sufficient to describe the experimental perecentage yields and its results are compared with the ones obtained using the B3LYP/6-31G*.

Optimisation and Structures of Transition States at HF/3-21G Level of Theory

The optimised structures of the four transition states from the AM1 calculations are reoptimised and their frequencies calculated at the HF/3-21G level of theory. The options used in the calculations are the same as the one used in the B3LYP/6-31G* calculations. 6-endo (HF/3-21G): DOI:10042/to-4197 , 5-endo (HF/3-21G): DOI:10042/to-4198 , 6-exo (HF/3-21G): DOI:10042/to-4199 , 5-exo (HF/3-21G): DOI:10042/to-4200 .

The optimised structures of the four transition states and some of its properties are given in the table below.

Comparison Between the Four Transition States at the HF/3-21G Level

Parameter	6-endo	5-endo	6-exo	5-exo
Structure	5-endo TS	5-endo TS	6-exo TS	5-exo TS
Energy (Hartrees)	-964.94833389	-964.94355123	-964.94471093	-964.94028039
Imaginary Frequency (cm-1)	-757	-777	-751	-769
Bond Length of the Partially Formed σ C-C Bond (Å)	2.19, 2.16	2.08, 2.28	2.22, 2.16	2.10, 2.29

Comparing the optimised structures of the four transition states obtained using the two levels of theory, it is discovered that the optimised structures are about the same for each transition state. The only main difference is the bond length of the partially formed σ C-C bond with different methods giving different bond lengths. However, it is found that the longer bond length within a form of the transition state from the B3LYP/6-31G* calculations is still longer in the same form of transition state in HF/3-21G calculations. This means that the longer partially formed σ C-C bond in any of the four transition states will always be calculated to have a larger bond length value, irrespective of the level of theory used, just that its numerical value could be different.

All the optimised transition states show a negative imaginary frequency each, and the vibrations at these frequencies correspond to this Diels Alder reaction. The values of the imaginary frequencies given by the HF/3-21G method are different from that given by the B3LYP/6-31G* method, but the order of the values (magnitude-wise) is still the same with the 5-endo form having the most negative frequency, followed by the 5-exo form, 6-endo form and 6-exo form. The energies of the four transition states given by the HF/3-21G method are different than that from the B3LYP/6-31G* method, but this is again expected due to the different considerations used in the calculations. However, both calculation methods give the 6-endo form as the most stable form of the transition state as its energy value is the lowest (more negative) than the other forms of transition states. The relative energy levels of the other forms of the transition states when compared to the 6-endo form is given below.

Relative Energy Levels of the Four Forms of Transition States And The Percentage Yields (HF/3-21G)

Configuration	Relative Energy Levels, ΔHrel (kcal/mol)	Reported Percentage Yields
6-endo	0.000	58%
5-endo	3.001	25%
6-exo	2.273	17%
5-exo	5.054	0%

The HF/3-21G level of theory is found to be able to explain the percentage yields of the 6-endo and 5-exo products as the 6-endo transition state is calculated to be the most stable (lowest activation energy) while the 5-exo transition state is calculated to be the least stable (highest activation energy). However, this method is not able to clearly explain the percentage yields for 5-endo and 6-exo products. According to calculations at the HF/3-21 level of theory, the 5-endo transition state is significantly more destabilised than the 6-exo transition state (difference of 0.728 kcal/mol) but this is not consistent with the experimental percentage yields which suggests that the 5-endo transition state has a lower energy than the 6-exo transition state due to the higher percentage yield of the 5-endo product. This shows the failure of the HF/3-21G level of theory in explaining the percentage yields of the 5-endo and 6-exo products.

In conclusion, the B3LYP/6-31G* level of theory is found to be useful in explaining all of the experimental percentage yields but the same cannot be said about the HF/3-21G level of theory. The HF/3-21G level of theory can only be used to explain the percentage yields of the 6-endo and 5-exo products but it predicts the percentage yields of the 5-endo and 6-exo products inaccurately as the relative stabilities of the two forms are different from the ones from the B3LYP/6-31G* level of theory. The B3LYP/6-31G* level of theory is still a better method for the analysis of the products of this Diels Alder reaction.