Rep:Mod:kmt07232

Borane BH₃

Optimisation and Structure

The structure of borane, BH₃, is optimised using the DFT: B3LYP method with the 3-21G basis set with all B-H bond lengths originally set at 1.5Å. After optimisation, all the three B-H bond lengths are the same (1.19Å) and the H-B-H bond angles are all 120.0°. The calculated B-H bond length is found to be consistent with the value reported in literature (B-H bond distance = 1.1867Å ). The optimised structure of BH₃ and the calculation summary of the optimisation are given below.

BH3

BH₃ Optimisation Calculation Summary

File Name	khaiming_bh3_opt
File Type	.log
Calculation Type	FOPT
Calculation Method	RB3LYP
Basis Set	3-21G
Charge	0
Spin	Singlet
E(RB3LYP)	-26.46226338 a.u.
RMS Gradient Norm	0.00020672 a.u.
Imaginary Freq	-
Dipole Moment	0.0000 Debye
Point Group	D3h
Job CPU Time	0 days 0 hours 0 minutes 27.0 seconds

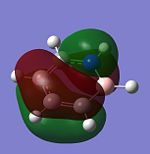
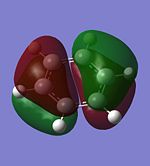
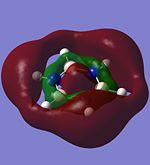
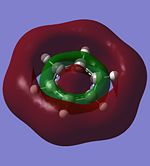
MO Diagram

The molecular orbitals of trigonal planar D_3h BH₃ can be predicted using the LCAO method by considering two fragments, the central element B and the H₃ fragment. The H₃ fragment has 3 fragment orbitals (two degenerate e' and one a₁') while the B atom uses its 1s, 2s, 2p_x, 2p_y and 2p_z atomic orbitals to form the molecular orbitals of BH₃. The relative energy levels and shapes of the molecular orbitals derived from the LCAO method are shown in the MO diagram.

The molecular orbitals of BH₃ can also be calculated from the optimised structure of BH₃. This can be done by selecting the energy option in the Gaussian calculation and the "Full NBO" option in the NBO tab, and also using the additional keywords "pop=full". The results file from the population and MO analysis is shown below. The calculated or the so-called "real" molecular orbitals are shown in the MO diagram, next to their corresponding LCAO molecular orbitals. Population and MO Analysis : https://www.ch.ic.ac.uk/wiki/images/f/ff/KHAIMING_BH3_POP.LOG

BH₃ Population and MO Analysis

File Name	khaiming_bh3_pop
File Type	.log
Calculation Type	SP
Calculation Method	RB3LYP
Basis Set	3-21G
Charge	0
Spin	Singlet
E(RB3LYP)	-26.46226338 a.u.
RMS Gradient Norm	-
Imaginary Freq	-
Dipole Moment	0.0000 Debye
Point Group	D3h
Job CPU Time	0 days 0 hours 0 minutes 16.0 seconds

The energy level of the molecular orbitals of BH₃ can be obtained from the results file and they are listed in the table below, together with the symmetry label and occupancy of the molecular orbitals.

Properties of the Molecular Orbitals of BH₃

No.	Energy Level (kJ/mol)	Symmetry Label	Occupancy
1	- 17 670	1a1'	Occupied
2	- 1 360	2a1'	Occupied
3	- 940	1e'	Occupied
4	- 940	1e'	Occupied
5	- 200	1a2	Vacant
6	500	2e'	Vacant
7	500	2e'	Vacant
8	510	3a1'	Vacant

It is learnt from the calculations that the energy level of the 3a₁' MO is slightly higher than that of the two degenerate 2e' MOs (energy difference approximately 10 kJ/mol). The relative position/ordering of the these orbitals is difficult to determine using the qualitative MO theory as we need to consider the strength of the s-s and s-p interactions, which is not easy to do. However, the computational method can easily give the relative energy level and ordering of the MOs. Comparing the "real" MOs obtained from the calculations with that generated from the LCAO method, it is found that there is a very good match between both MOs. The MOs generated using the LCAO method (qualitative MO theory) look very similar to the real MOs of BH₃. Hence, the qualitative MO theory is very useful in generating the shapes of MOs for molecules but it is not very accurate in determining the relative ordering of some MOs unless additional information about the molecule is given (such as relative strength of orbital interactions).

Vibrational Frequencies and IR Spectrum

The vibrational frequencies of BH₃ and its IR spectrum can be calculated using Gaussian by choosing the "Frequency" option. At the same, the result from this calculation can be used to perform frequency analysis to determine whether the optimised structure is indeed the one with minimum energy. From the calculation results summary, the energy of the structure is found to be the same as the one obtained from the optimisation (-26.46226338 a.u.). Therefore, the optimised structure of BH₃ is correct and it has the lowest energy. The vibrations of BH₃ and their corresponding frequencies and intensities are summarised in the table below. Vibrational Frequency and IR Spectrum: https://www.ch.imperial.ac.uk/wiki/images/9/94/KHAIMING_BH3_FREQ.LOG

Vibrations of BH₃ and Their Frequencies, Intensities and Symmetries

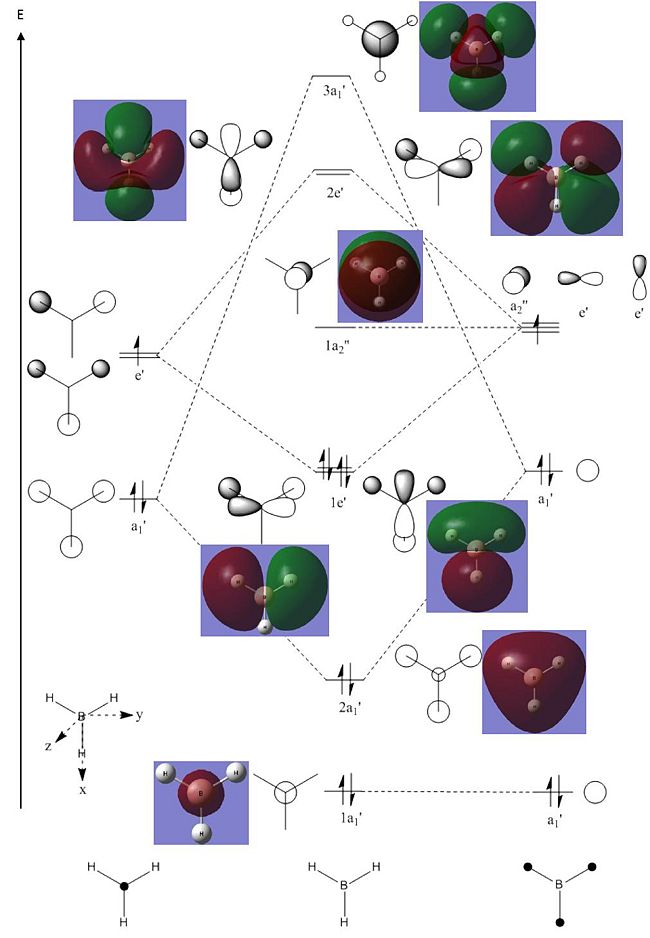
No.	Form of the Vibration	Frequency (cm-1)	Intensity	Symmetry (D3h Point Group)	Literature Frequency (cm-1)
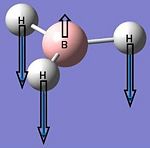1	Bending vibration. All three H atoms are moving up and down the BH3 plane together in a concerted motion, while the centre B atom moves in the opposite direction with a smaller displacement .	1144	93	A2"	1147
2	Bending vibration. Two of the H atoms move towards and away from each other in a scissoring manner in a concerted motion, while the other H atom and the B atom move together along their B-H bond with a smaller displacement.	1204	12	E'	1197
3	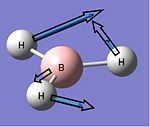Bending vibration. Two of the H atoms and the B atom are moving in a rocking manner in the BH3 plane in a concerted motion, while the other H atom moves in a larger displacement towards and away from one of the H atom doing the rocking motion.	1204	12	E'	1197
4	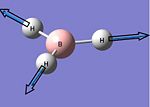Symmetric stretching. All the three H atoms move away and towards the centre B atom together in a concerted motion, while the B atom is stationary.	2598	0	A1'	-
5	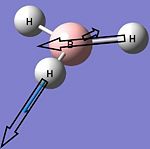Asymmetric stretching. One of the H atom moves towards the B atom while another H atom moves away from the B atom. Both stretchings are along their respective B-H bonds. The B atom moves in a smaller displacement towards the space between two H atoms, while the third H atom is stationary. All these motions are concerted.	2737	104	E'	2502
6	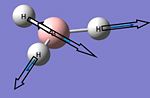Asymmetric stretching. Two of the H atoms move away from (and then towards) the B atom while the other H atom move towards (and then away from) the B atom, while the B atom move in a smaller displacement towards one of the H atom. All the stretches are concerted and are in the BH3.	2737	104	E'	2602

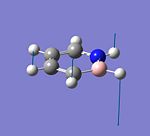
The type of bending and stretching of the BH₃ molecule is determined from Infrared Absoprtion Spectroscopy - Theoretical Principles.

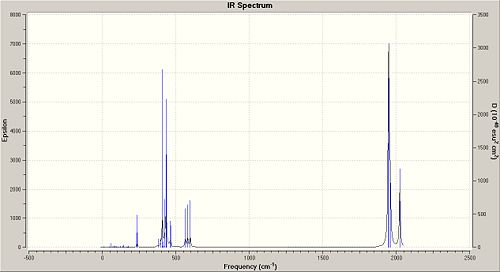
There are 6 vibrations calculated using Gaussian but one of them, the symmetric stretching (A₁') at 2598 cm^-1 has a zero intensity, causing this peak at 2598 cm^-1 to be not observed in the IR spectrum of BH₃. This is because there is no change in dipole moment during this vibration as the stretching is symmetric and the changes in dipole moment due to the B-H stretches are all cancelled out (BH₃ molecule has the D_3h point group). Only three peaks are observed in the IR spectrum and this is consistent with the calculated vibrations and its frequencies. There are two E' bending vibrations that have the same vibrational frequency (1204 cm^-1) and another two E' asymmetric stretches that have the same vibrational frequency (2737 cm^-1). This causes the number of observed peaks in the IR spectrum to be 3 and not 5 (also not 6 as the intensity of the peak at 2598 cm^-1 is zero). Comparing the vibrational frequencies with that given in the literature, it is found that the calculated vibrational frequencies for the first three vibrations are a good match with that in the literature as their difference in wavenumbers is less than 10 cm^-1. The peak due to the symmetric stretch is not reported in literature, and this probably due to its calculated zero intensity. However, there is a very bad match between the reported and calculated vibrational frequencies for the asymmetric stretches as their frequencies differ by more than 100 cm^-1. This could be due to the limitation of the Gaussian calculation used (DFT, B3LYP method with the 3-21G basis set) and also the difference in the method used to get the values in the literature (CBS CCSD(T) + AUX Quartic Force Field).

The corresponding IR spectrum of BH₃ obtained from the Gaussian calculation is given below.

Boron Trichloride BCl₃

Optimisation and Frequency Analysis

The structure of BCl₃ is optimised using the DFT: B3LYP method with the LanL2MB option and the point group of the molecule restricted to the D_3h point group. After optimisation, the three B-Cl bonds are found to have an identical bond length, which is 1.87Å. The optimised Cl-B-Cl bond angle is 120.0° and the point group of the BCl₃ molecule is D_3h (due to the restriction). The optimised bond length is found to be longer than the one reported in literature, 1.74Å and this is probably due to the basis set used to optimise BCl₃. The LanL2MB basis set may not be suitable for the optimisation of this molecule as the Cl atom could still be considered as a "light" element and the pseudo potential consideration is not required. The use of another method, MBPT(2) with the combination of ECP-1/VAL-1 basis set for the optimisation has been shown to give a more accurate B-Cl bond length (1.742Å). On the other hand, the optimised Cl-B-Cl bond angle is exactly the same as the experimental value, 120°. The optimised structure of BCl₃ and the calculation summary are given below.

BCl3

BCl₃ Optimisation Calculation Summary

File Name	khaiming_bcl3_opt
File Type	.log
Calculation Type	FOPT
Calculation Method	RB3LYP
Basis Set	LANL2MB
Charge	0
Spin	Singlet
E(RB3LYP)	-69.43928112 a.u.
RMS Gradient Norm	0.00005905 a.u.
Imaginary Freq	-
Dipole Moment	0.0000 Debye
Point Group	D3h
Job CPU Time	0 days 0 hours 0 minutes 17.0 seconds

The frequency analysis is then performed on the optimised BCl₃ molecule to determine whether the optimised structure is indeed the one at ground state with the minimum potential energy, and not a transition state. In order to determine this, the energies obtained from the optimisation and the frequency calculations need to be compared. As the use of different method and basis set will give completely different energy values (due to the different considerations involved in different methods), in order to accurately compare both energy values from the optimisation and frequency calculations, the same method and basis set must be used for both calculations. In this case, it is found that both energies obtained from the optimisation and frequency calculations are the same (-69.43928112 a.u.). Hence, the optimised structure is indeed the one with the lowest energy. Frequency Calculations: https://www.ch.imperial.ac.uk/wiki/images/5/54/KHAIMING_BCL3_FREQ.LOG

The following table gives the calculated vibrational frequencies of BCl₃ and their corresponding intensities and symmetries. The six vibrations are almost similar to the ones calculated for BH₃ but their frequencies are different than the ones for BH₃. In general, all the vibrational frequencies of BCl₃ are smaller than the equivalent ones in BH₃. This is due to the difference in the atomic mass of the atoms - Cl is much heavier than the H atom, hence, the vibrations are harder for BCl₃ than for BH₃ (easier to bend and stretch the B-H bonds than B-Cl bonds). Besides that, the usage of different basis sets to calculate the vibrations of both molecules may contribute to the difference in the frequencies but this difference may not be very large. A thing to note is that the A₁' symmetric stretch of BCl₃ has a zero intensity. This is similar to the BH₃ case and can be explained using the no change in dipole moment due to the symmetric stretch in BCl₃.

Vibrational Frequencies of BCl₃ and their Intensities and Symmetries

No.	Vibrational Frequency (cm-1)	Intensity	Symmetry (D3h Point Group)
1	214	4	E'
2	214	4	E'
3	377	44	A2"
4	417	0	A1'
5	939	259	E'
6	939	259	E'

The ground state structure of BCl₃ is expected to be a trigonal planar (from VSEPR theory) with the D_3h point group. Gaussian will try to optimise the structure of BCl₃ in all possible symmetry point groups if the point group is not restricted before the Gaussian optimisation calculation. This causes Gaussian to take a slightly longer time (20 seconds for the calculation without point group restriction vs 17 seconds for the one with D_3h restriction) to find the optimised structure of BCl₃ but it will eventually give the D_3h point group in the result.

Discussion on Bonds

"Missing" Bonds in Gaussview

Gaussview can at times omit bonds between two atoms in some optimised structures where we expect to have chemical bonds. Although the bond is not drawn, this does not mean that there is no bond between the two atoms. The bond may exist but its bond length is more than or less than the range of specified bond lengths stored in the Gaussview database. This causes Gaussview to not recognise the presence of the bond, hence, it is not drawn in the optimised structure. As most of the bond length range in the Gaussview database is based on organic compounds, it is very common to have bond "missing" in the structures of inorganic molecules due to the possibility of different bond lengths in inorganic compounds.

Definition of Bond

A chemical bond is a type of attractive force that holds two or more atoms together in a chemical species and can be considered as the interaction between the atoms. These bonds can have different bond strengths, and they can usually be divided into strong bonds and weak bonds. Strong bonds include ionic bonds, covalent bonds and metallic bonds while some examples of weak bonds are the hydrogen bonding, dipole-dipole interactions and the London dispersion forces. Ionic bonds are formed in ionic compounds from the electrostatic attraction between a positively charged cation and a negatively charged anion while the metallic bond is found in metals between the cations and the sea of delocalised electrons around the cations. Covalent bonds are usually found in non-ionic and non-metallic compounds with the two atoms being held by the attractive force between the positively charged nuclei and the shared electrons which have a very high probability of being found in between the two atoms.

Isomers of Mo(CO)₄(PCl₃)₂

The Mo(CO)₄(PCl₃)₂ complex can exist in either the cis or trans-isomer form. The cic-isomer has the two PCl₃ ligands next to each other while the two PCl₃ groups are opposite each other in the trans-isomer. Both isomers are initially optimised using the DFT: B3LYP method with the LANL2MB basis set and the option "loose" to get the rough geometry of the Mo complex. Then, the two PCl₃ ligands are rotated in different ways for both isomers before a second optimisation is performed using the DFT: B3LYP method with the LANL2DZ basis set and a higher electronic convergence. The frequency analysis is then performed on the optimised structures of the cis- and trans-isomers to determine the validity of the minimum point (optimised structure) and the vibrational frequencies of both isomers.

Optimisation and Frequency Analysis of Isomers

The results from the optimisation calculations of both isomers are shown in the table below. Cis-isomer: DOI:10042/to-3791 , trans-isomer DOI:10042/to-3792 .

Cis- and Trans-Mo(CO)₄(PCl₃)₂ Optimisation Calculations Summary

	Cis Mo(CO)4(PCl3)2	Trans Mo(CO)4(PCl3)2
File Name	log_23256	log_23262
File Type	.log	.log
Calculation Type	FOPT	FOPT
Calculation Method	RB3LYP	RB3LYP
Basis Set	LANL2DZ	LANL2DZ
Charge	0	0
Spin	Singlet	Singlet
E(RB3LYP)	-623.57707194 a.u.	-623.57603103 a.u.
RMS Gradient Norm	0.00000618 a.u.	0.00002917 a.u.
Imaginary Freq	-	-
Dipole Moment	1.3101 Debye	0.3049 Debye
Point Group	C1	C1
Job CPU Time	0 days 0 hours 58 minutes 36.7 seconds	0 days 0 hours 44 minutes 18.8 seconds

Frequency analysis gives energy values that are exactly the same as the ones given in the optimisation calculations (cis-isomer: DOI:10042/to-3793 , trans-isomer: DOI:10042/to-3794 ). This confirms that the optimised structures of both isomers are minimum points with the lowest energy values.

Structures of Isomers

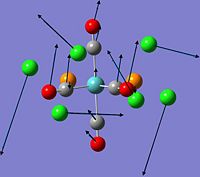
The optimised structures of the cis- and trans-isomer calculated using Gaussian are given below.

Cis Mo(CO)₄(PCl₃)₂

Cis-isomer

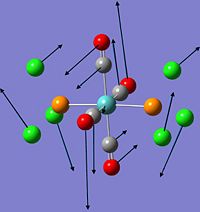
Trans Mo(CO)₄(PCl₃)₂

Trans-isomer

The cis-isomer has a higher dipole moment (1.31D) than the trans-isomer (0.30D) and this is expected from their optimised structures. The dipole moments due to the two PCl₃ and two CO ligands are not cancelled out in the cis-isomer as the same types of ligands are not opposite to each other, hence, the cis-isomer has a high dipole moment. On the other hand, the trans-isomer has an almost zero dipole moment as all the same types of ligands are almost opposite each other, causing the dipole moments to be almost cancelled out. Some of the bond lengths and bond angles in both Mo(CO)₄(PCl₃)₂ isomers are compared with the ones reported in literature for cis and trans Mo(CO)₄(PPh₃)₂ in the table below.

Comparisons of Bond Lengths and Bond Angles in the Mo Complexes

Parameter	Cis Mo(CO)4(PCl3)2	Cis Mo(CO)4(PPh3)2	Trans Mo(CO)4(PCl3)2	Trans Mo(CO)4(PPh3)2
Mo-P Bond Length (Å)	2.51	2.576, 2.577	2.44	2.500
Mo-C Bond Length (Å)	2.01 (for the 2 cis CO), 2.06 (for the 2 trans CO)	1.972, 1.973, 2.022, 2.059	2.06	2.016, 2.005
P-Cl Bond Length (Å)	2.24	-	2.24	-
CO Bond Length (Å)	1.18 (for the 2 cis CO), 1.17 (for the 2 trans CO)	1.158, 1.149, 1.136, 1.137	1.17	1.164, 1.165
P-Mo-P Bond Angle (°)	94.2	104.6	177.4	180.0
P-Mo-C Bond Angle (°)	89.2, 89.4, 91.9, 176.1 (2 equivalent sets)	163.7, 80.6, 94.0, 90.3, 91.7, 173.2, 90.6, 84.4	88.7, 90.0, 90.0, 91.3 (2 equivalent sets)	92.0, 87.2
Mo-C-O Bond Angle (°)	177.8, 177.9	-	179.2, 180.0	-

The Mo-P bond lengths in both Mo(CO)₄(PCl₃)₂ isomers are different from the ones given in literature as the one for literature is for the PPh₃ ligand. However, the Mo-P bond length is significantly shorter in the trans-isomer than it is in the cis-isomer of Mo(CO)₄(PCl₃)₂, and this is consistent with the values given in the literature (shorter Mo-P bond length in trans Mo(CO)₄(PPh₃)₂). All the Mo-C bond lengths of the trans-isomer are the same but there are 2 different Mo-C bond lengths in the cis-isomer. The 2.01Å bond length is for the 2 CO groups that are cis to each other, but for the trans CO groups, their Mo-C bond length is longer (2.06Å). The P-Cl bond lengths are the same for both isomers, suggesting that the P-Cl bonds are unaffected by the change in position of the PCl₃ ligand around the Mo centre. The CO bond length is about the same for both isomers (1.17 - 1.18Å) and this CO bond is between a double and a triple CO bond, as its bond length is between the bond lengths of the C=O (1.23Å) and C≡O (1.13Å).

The Mo-CO bonds in the trans-isomer is almost linear (Mo-C-O angle approximately 180°) but the ones in the cis-isomer is slightly bent (Mo-C-O angle approximately 178°). The P-Mo-P angles in both isomers are larger than the ideal angles in an octahedral but the deviation from octahedral structure is larger in the cis-isomer than the trans-isomer. The P-Mo-P angle is 94.2° in the cis-isomer when the angle is supposed to be 90.0° in a perfect octahedral (4.2° deviation) whereas in the trans-isomer, the P-Mo-P angle is 177.4° instead of 180° (2.6° deviation). All the CO ligands in both isomers are also not in the perfect octahedral arrangement as the bond angles between the ligand-Mo-ligand in both complexes are not equal to 90° (for cis groups) and 180° (for trans groups).

Relative Energies of Isomers

Comparing the energies of both isomers, it is found that the cis-isomer has a slightly lower energy than the trans-isomer with a very small energy difference of 3 kJ/mol. As the cis-isomer is found to have the lower energy level, it is more stable than the trans-isomer. The relative stability of the two isomers depends on the electronic and sterics stabilisation of the complex. The complex is said to be electronically stable if the number of trans CO pairs is minimised in the complex while it is sterically more stable if there are less bulky ligands being close together in the complex. In the cis-isomer, although the two bulky PCl₃ ligands are next/cis to each other, the sterics effect is minimised by increasing the Mo-P bond length (2.51Å vs 2.44Å in trans-isomer) and the Cl atoms are arranged in such a way to minimise contact between the two groups. In addtion to that, there is only one trans CO pair in the cis-isomer (trans-isomer has two trans CO pair), making the cis-isomer more electronically stable. Stabilisation by the electronic effect and the minimisation of the sterics effect make the cis-isomer more stable than the trans-isomer.

Interestingly, if the optimisation process of both Mo(CO)₄(PCl₃)₂ isomers are repeated using the additional extrabasis option which considers the low-lying d orbitals of the P atom, it is found that the trans-isomer is now more stable than the cis isomer as the trans-isomer has a lower energy, with an energy difference of approximately 3 kJ/mol (cis-isomer(with extrabasis): DOI:10042/to-3799 , trans-isomer(with extrabasis): DOI:10042/to-3800 ). This is in fact the reverse of the results obtained using only the LANL2DZ pseudo-potential and its associated basis set. This corresponds well with the report in literature where the trans Mo(CO)₄(PPh₃)₂ is found to be thermodynamically more stable than the cis isomer. In this case, the sterics stablisation seems to be more important than the electronic stabilisation. Also, the consideration of d orbitals is good for the Mo(CO)₄(PPh₃)₂ complex as the d orbitals on the P atoms may be able to interact with the π orbitals and electrons on the phenyl substituent.

Vibrational Frequencies of Isomers

The vibrational frequencies of both the cis and trans isomer of Mo(CO)₄(PCl₃)₂ are obtained from the frequency calculations of the isomers. It is found that the there are two low frequency vibrations for each of the isomers and they are shown in the table below. These low frequency vibrations which are due to the rocking motions, require very low energy to occur, hence, the Mo complex can have sufficient energy at room temperature to undergo these rocking motions.

Low Frequency Vibrations of the Cis- and Trans-isomers and Their Intensities and Symmetries

Complex	Form of the Vibration	Frequency (cm-1)	Intensity	Symmetry
Cis Mo(CO)4(PCl3)2	Rocking motion. The Mo(CO)4 unit moves in a concerted rocking motion, while the other two PCl3 groups also undergo rocking motion, but not in the same phase as the Mo(CO)4 unit.	11	0	A
Cis Mo(CO)4(PCl3)2	Rocking motion. The four CO groups move in a concerted rocking motion but the central Mo atom remains stationary. The other two PCl3 groups also undergo rocking motion, but not in the same phase as the CO groups.	18	0	A
Trans Mo(CO)4(PCl3)2	Rocking motion. The Mo(CO)4 unit moves in a concerted rocking motion, while the Cl atoms of the PCl3 ligands also undergo rocking motion, but not in the same phase as the Mo(CO)4 unit. However, both P atoms remain stationary.	5	0	A
Trans Mo(CO)4(PCl3)2	Rocking motion. Two CO groups which are trans to each other move in a concerted rocking motion but the central Mo atom and the other two CO groups remain stationary. The Cl atoms on both PCl3 ligands also move in a rocking motion but they move in the opposite phase with each other and the P atoms are stationary.	6	0	A

There are four carbonyl ligands around the Mo metal centre and they can have different positions in the Mo complex, as seen in the cis- and trans-isomer. The different positions of the carbonyl group gives rise to different symmetries for the cis- and trans-isomer. Without considering the geometry and symmetry of the PCl₃ ligand, the cis-isomer is ideally of C_2v symmetry while the trans-isomer is ideally of D_4h symmetry. However, the symmetry is reduced after considering the symmetry of the PCl₃ ligands, however, the symmetry of the trans-isomer is still higher than the one in the cis-isomer. This difference in symmetry in the cis and trans Mo(CO)₄(PCl₃)₂ results in the different number of CO stretching frequencies observed in the IR spectrum. The cis-isomer is expected to show four CO peaks while only one CO peak is expected in the trans-isomer. In addition to that, the CO stretching frequencies in both isomers are expected to be different as the CO ligands in the two isomers are in different chemical environments due to different positions of the PCl₃ ligands. The calculated carbonyl stretching frequencies and their intensities in both isomers are compared with the values reported in literature in the tables below.

CO Stretching Frequencies and Intensities in Cis Mo(CO)₄(PCl₃)₂

Calculated CO Stretching Frequency (cm-1)	Intensity	Reported CO Stretching Frequency (cm-1)	Symmetry
1945	763	1986	B2
1949	1498	1994	B1
1958	633	2004	A1
2023	598	2072	A1

Comparing the calculated CO stretching frequencies with that in the literature, it is found that the calculated frequencies given by Gaussian is quite a poor match with the experimental results as all the calculated CO stretching frequencies are much smaller than the ones reported in literature. This is probably due to the fact that Gaussian considers the Mo complex to be in the gas phase when calculating the virational frequencies but the experimental values are obtained from the liquid or solution form of the Mo complex. However, the number of peaks due to CO stretchings obtained from Gaussian is consistent with the one in literature. There are four CO peaks observed in the IR spectrum as all the stretches are IR active due to the absence of symmetric CO stretch in the Mo complex as the CO groups are not symmetrically arranged around the Mo centre.

CO Stretching Frequencies and Intensities in Trans Mo(CO)₄(PCl₃)₂

Calculated CO Stretching Frequency (cm-1)	Intensity	Reported CO Stretching Frequency (cm-1)	Symmetry
1950	1475	1896	Eu
1951	1467	-	-
1977	1	-	-
2031	4	-	-

There are four calculated CO stretching frequencies but two of them (1977 and 2031 cm^-1) are not observed in the IR spectrum as their intensities are very small. Their small intensities are due to the fact that the CO stretches are not IR active as there is no change in dipole moment during these CO symmetric stretches. The other two peaks due to CO stretches are very close to each other (1 cm^-1 difference), causing them to appear as a single peak in the IR spectrum. This means that overall, only one CO stretching peak is observed in the IR spectrum and this is consistent with the result given in the literature. However, there is a poor match in the frequency values between the calculated and experimental results. This is again due to the fact that the vibrational frequency is calculated in the gas phase for Gaussian but recorded in the liquid/solution form in experiments.

Some of the stretching frequencies and the corresponding intensities of cis and trans Mo(CO)₄(PCl₃)₂ are given in the tables below.

Stretching Frequencies and Intensities of Cis Mo(CO)₄(PCl₃)₂

Stretching Frequency (cm-1)	Intensity	Assignment
235	13	Mo-P stretch
236	29	Mo-P stretch
405	2	Mo-C stretch
425	77	Mo-C stretch
432	241	Mo-C stretch
459	46	Mo-C and Mo-P stretches in the equatorial plane
1945	763	CO Stretch (2 CO groups trans to PCl3, out of phase with each other)
1949	1498	CO Stretch (2 CO groups trans to each other, out of phase with each other)
1958	633	CO Stretch (4 CO groups but 2 are out of phase with the other 2)
2023	598	CO Stretch (4 CO groups)

Stretching Frequencies and Intensities of Trans Mo(CO)₄(PCl₃)₂

Stretching Frequency (cm-1)	Intensity	Assignment
240	0	Mo-P stretch (symmetric)
252	38	Mo-P stretch (asymmetric)
389	2	Mo-C stretch (1 pair of trans CO)
389	0	Mo-C stretch (the other pair of trans CO)
401	4	Mo-C stretch (3 CO groups)
407	0	Mo-C and Mo-P stretches (symmetric)
409	728	Mo-P stretch (asymmetric)
423	168	Mo-C stretch (1 pair of trans CO)
426	166	Mo-C stretch (the other pair of trans CO)
458	0	Mo-P stretch (symmetric)
1950	1475	CO Stretch (2 CO groups, out of phase with each other)
1951	1467	CO Stretch (2 CO groups, out of phase with each other)
1977	1	CO Stretch (4 CO groups, symmetric, but 2 are out of phase with the other 2)
2031	4	CO Stretch (4 CO groups, symmetric)

The predicted IR spectrum of cis Mo(CO)₄(PCl₃)₂ is shown below on the left while the one for trans Mo(CO)₄(PCl₃)₂ is on the right.

Miniproject: 1,2-azaborines And Its Derivatives

This mini project is on the hybrid organic/inorganic structure, 1,2-azaborine (C₄H₆BN) which has a cyclic structure that resembles the one in benzene and borazine. 1,2-azaborine compounds were first reported in the 1960s by Dewar and White but their synthesis and isolation, especially that of the parent 1,2-dihydro-1,2-azaborine were difficult to achieve at that time, suggesting that these compounds are reactive and chemically unstable. However, in recent years, research groups such as Marwitz et al and Ashe et al, have devised a series of effective synthetic steps that leads to the successful preparation and isolation of 1,2-azaborines, creating a new interest in the study of these compounds. This mini project aims to study the structure, charge distributions, vibrations and molecular orbitals of the parent 1,2-azaborine and their similarities or differences with borazine and benzene. Then, a reaction involving a 1,2-azaborine derivative is studied and the products of this reaction are compared (population and MO analysis, vibrational frequency analysis and natural bond order analysis).

The method used in the Gaussian calculations is the DFT: B3LYP method for all structures. Structures are first optimised using the LANL2MB basis set before a second optimisation is done using the 6-311G (d,p) basis set with the additional keywords: int=ultrafine and scf=conver=9. Frequency analysis is always performed to check the optimised structure given by Gaussian after the second optimisation.

Optimisation of 1,2-azaborine, Borazine and Benzene

The results from the optimisation calculations of C₄H₆BN, B₃N₃H₆ and C₆H₆ are shown in the table below. C₄H₆BN: DOI:10042/to-3816 , B₃N₃H₆ DOI:10042/to-3815 , C₆H₆: DOI:10042/to-3817 .

C₄H₆BN, B₃N₃H₆ and C₆H₆ Optimisation Calculations Summary

	C4H6BN	B3N3H6	C6H6
File Name	log_23440	log_23438	log_23441
File Type	.log	.log	.log
Calculation Type	FOPT	FOPT	FOPT
Calculation Method	RB3LYP	RB3LYP	RB3LYP
Basis Set	6-311G(d,p)	6-311G(d,p)	6-311G(d,p)
Charge	0	0	0
Spin	Singlet	Singlet	Singlet
E(RB3LYP)	-235.74293299 a.u.	-242.74448809 a.u.	-232.30854448 a.u.
RMS Gradient Norm	0.00013404 a.u.	0.00025339 a.u.	0.00003422 a.u.
Imaginary Freq	-	-	-
Dipole Moment	2.1642 Debye	0.0001 Debye	0.0000 Debye
Point Group	C1	C1	C1
Job CPU Time	0 days 0 hours 13 minutes 21.1 seconds	0 days 0 hours 8 minutes 33.1 seconds	0 days 0 hours 8 minutes 18.0 seconds

Frequency analysis confirms that the optimised structures given after the second optimisation is the ground state with the minimum energy, and not a transition state. The energy values from the frequency calculations are the same with the one from the optimisation calculations. C₄H₆BN: DOI:10042/to-3819 , B₃N₃H₆ DOI:10042/to-3818 , C₆H₆: DOI:10042/to-3820

Structures and Charge Distributions of 1,2-azaborine, Borazine and Benzene

The optimised structures of C₄H₆BN, B₃N₃H₆ and C₆H₆ are given below:

C₄H₆BN

C4H6BN

B₃N₃H₆

B3N3H6

C₆H₆

C6H6

The C-C bond lengths in C₆H₆ are all the same (1.39Å), with the C-C-C bond angles all the same (120.0°). The C-H bond lengths are also the same (1.08Å). For B₃N₃H₆, all the B-N bond lengths are the same (1.43Å), the B-H bond lengths are the same (1.19Å) and the N-H bond lengths are the same (1.01Å). There are 2 different bond angles, with the angle of N-B-N equals to 117.0° and B-N-B equals to 123.0°.

For the 1,2-azaborine, its B-N bond length is 1.44Å, which is about the same as the B-N bond in borazine. This B-N bond length is in between that of a single and double B-N bonds (1.51Å and 1.31Å), suggesting that there is partial delocalisation of the lone pair on N. The C-H (1.08Å), B-H (1.19Å) and N-H (1.01Å) bond lengths in 1,2-azaborine are the same as the ones in benzene and borazine, but there are two very distinct C-C bond lengths (1.37Å and 1.42Å) in 1,2-azaborine. This suggests that there is a difference in the C-C bonds in 1,2-azaborine, with one of the C-C bond being more of a single bond while the other two C-C bonds are more of a double bond. These C-C bonds are different from the one in the benzene, where all the C-C bonds are the same and in between a single and double C-C bond. However, these bond lengths are still between the C-C single and double bond lengths (1.47Å and 1.35Å). This means that there is some delocalisation of the π electrons, but it is not as delocalised as the delocalisation in the benzene ring. The partial delocalisation of the lone pair on N and the π electrons of the C atoms will give some stability to 1,2-azaborine and this explains the substantial aromatic character reported in 1,2-azaborine. The C-N and C-B bond lengths in 1,2-azaborine are calculated to be 1.37Å and 1.51Å.

Comparison of Calculated Bond Lengths in 1,2-azaborines with Literature

Bond	Calculated Bond Length (Å)	Lit. Bond Length (Å)
N-B	1.44	1.43
B-C	1.57	1.52
C3-C4	1.37	1.35
C4-C5	1.42	1.44
C5-C6	1.37	1.35
C-N	1.37	1.36

There is a good match between the calculated bond lengths of 1,2-azaborine with the reported in literature. The slight difference is cause by the use of a different method in the calculations done in the literature (spin-restricted Hartree-Fock SCF-level with the 6-31G* basis set).

For 1,2-azaborine, the ring angle centred at N is 123.5°, which is larger than the one in borazine, while the ring angle centred at B is 114.8°, which is very much smaller than the one calculated for borazine. As C-B and N-B bonds are quite long, the B atom is slightly "pushed" out of the ring and the angle at B is reduced. This causes the 1,2-azaborine molecule to be slightly squeezed with the B atom slightly sticking out of the ring. However, the 6-membered ring of 1,2-azaborine remains planar, just like benzene and borazine.

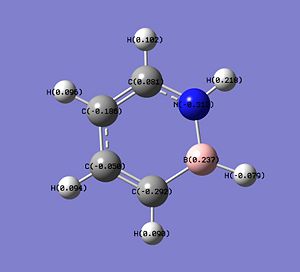
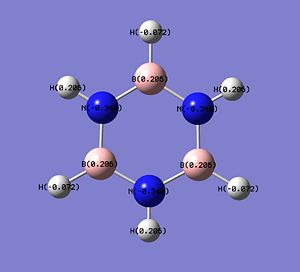
The charge distributions in the molecules of C₄H₆BN, B₃N₃H₆ and C₆H₆ are shown below.

Charge Distributions in C₄H₆BN, B₃N₃H₆ and C₆H₆

C4H6BN	B3N3H6	C6H6

In 1,2-azaborine, the H atom connected to the N atom has a slight positive charge (+0.218: low electron density), making it protic and can act as H⁺ in some reactions. This proton is in fact more protic than the equivalent proton in the borazine (+0.206), making it more useful as a H⁺ source. On the other hand, the H atom connected to the B atom is not very hydridic as it only has a very small negative charge (-0.079) and is only slightly more hydridic than the one in borazine (-0.072). The B atom of 1,2-azaborine has a more positive charge than the one in borazine (+0.237 vs +0.206) suggesting that the B atom in 1,2-azaborine is more susceptible to nucleophilic attack. Another important result from the charge distribution analysis is that the C atoms at the 3 and 5 position have considerably high partial negative charges, -0.292 and -0.186, which is much higher than the one observed on the C atom of benzene (-0.095). This means that 1,2-azoborines are more reactive than benzene. As these two C atoms are more negative than the other two C atoms in 1,2-azoborine, the electrophilic aromatic substitutions occur exclusively at the 3 and 5 position, with the attack at the 3 position more likely due to the higher partial negative charge on the C at the 3 position.

The dipole moment of 1,2-azoborines is also quite high (2.16D) as all the dipole moments in the molecule is not cancelled out due to the asymmetric distribution of charges in the molecule. Structures such as benzene and borazine have the charges on the atoms symmetrically arranged in the molecule, causing all the dipole moments in the molecule to be cancelled out, leaving them to have a dipole moment of 0.00D.

Natural Bond Order Analysis of 1,2-azaborine, Borazine and Benzene

The natural bond order analysis of selected bonds in 1,2-azaborine is summarised in the table below. C₄H₆BN: DOI:10042/to-3819 , B₃N₃H₆ DOI:10042/to-3818 , C₆H₆: DOI:10042/to-3820

Natural Bond Analysis of 1,2-azaborine

Bond	Occupancy	Atomic Contributions	Orbitals Involved	Comment
C-N	2e-	37.93% from C; 62.07% from N	C: 30.04%(s), 69.86%(p), 0.10%(d); N: 34.50%(s), 65.45%(p), 0.05%(d)	d orbitals of the C and N atoms do not contribute much to the bonding, it can be assumed that it is not involved in this bonding. The C and N atoms use their sp2 hybrid orbitals (approximately) to form this bond, with the N atom contributing more to this bond than the C atom. This bond is the σ bond between C and N.
C-B	2e-	65.21% from C; 34.79% from B	C: 37.77%(s), 62.20%(p), 0.03%(d); B: 36.89%(s), 63.08%(p), 0.04%(d)	d orbitals can be assumed to be not involved in this bonding. The C atom contributes more to this bond than the B atom with each atom using a hybrid orbital that looks like the sp2 to form this bond. This is the σ bond between C and N.
N-H	2e-	70.09% from N; 29.91% from H	N: 22.61%(s), 77.34%(p), 0.05%(d); H: 99.93%(s), 0.07%(p)	This is the σ bond between N and H, with the N atom contributing more than the H atom in the bonding. The H atom uses its s orbital to form this bond, with no contribution from the p and d orbitals, while the N atom uses the sp3 hybrid orbital (approximately) with no contribution from the d orbital.
B-H	2e-	46.13% from B; 53.87% from H	B: 35.60%(s), 64.36%(p), 0.04%(d); H: 99.92%(s), 0.08%(p)	This is the σ bond between B and H, with the H atom contributing slightly more than the B atom in the bonding (almost 50:50 contribution). The H atom uses its s orbital to form this bond, with no contribution from the p and d orbitals, while the B atom uses the sp2 hybrid orbital (approximately) with no contribution from the d orbital.
B-N	2e-	23.31% from B; 76.69% from N	B: 27.54%(s), 72.30%(p), 0.15%(d); N: 42.79%(s), 57.19%(p), 0.02%(d)	This is the σ bond between B and N, with the N atom contributing more than the B atom in the bonding. The B atom uses a sp3-like orbital for the bond, with very little contribution from the d orbital (but this is more than the other d orbital countributions in other bonds). The N atom uses more percentage of p orbital than the s orbital to form a hybrid orbital which is between the sp2 and sp orbitals for the B-N bond.
B-N	1.78e-	14.41% from B; 85.59% from N	B: 0.00%(s), 99.79%(p), 0.21%(d); N: 0.00%(s), 100%(p)	This is the π bond between B and N, with the N atom contributing much more than the B atom in the bonding. Both atoms do not use their s orbitals for this bond. For the N atom, it uses only the p orbital while the B atom almost uses only its p orbital as there is very little d orbital contribution (but this is more than the other d orbital countributions in other bonds).
C-C	2e-	50.15% from C; 49.85% from C	C: 40.58%(s), 59.38%(p), 0.04%(d); C: 35.93%(s), 64.02%(p), 0.05%(d)	This is the σ bond between the C atoms, with equal contributions from both C atoms in the bonding. One of the C atom uses the sp2 hybrid orbital for the bonding while the other C atom uses an orbital that looks like an intermediate between the sp2 and sp3 orbitals (41% s orbital, 59% p orbital). d orbitals contribution to the bonding is minimal.
C-C	1.78e-	46.36% from C; 53.64% from C	C: 0.00%(s), 99.95%(p), 0.05%(d); C: 0.00%(s), 99.96%(p), 0.04%(d)	This is the π bond between the two C atoms, with one of the C atom contributing slightly more than the other C atom in the bonding. Both C atoms use its p orbitals for this bond with very little contribution from the d orbitals.

The bond analysis shows that there is a π bond between the B and N atoms, just like the one between the C atoms with an electron occupancy of 1.78. This suggests that there are some delocalisation of electrons in 1,2-azaborine as all the π bonds have the same electron occupancy. The electron occupancy in all the σ bonds is the same, which is 2. Another thing to note is that the more electronegative atom will always contribute more than the more electropositive atom in the bonding between the two atoms. This is shown in the bonds between C-N, C-B, B-N and N-H. If the electronegative difference between the two atoms that form a bond is very small (B-H and C-C), there will be an almost equal contribution from both atoms in the bonding. The d orbitals do not conrtibute much in the bondings between the atoms in the 1,2-azaborine but they could be important in the formation of anti-bonding orbitals.

The bond analysis of the B-N bond in borazine and the C-C bond in benzene is shown below.

Bond Analysis in Benzene and Borazine

Bond	Occupancy	Atomic Contributions	Orbitals Involved
C-C (benzene) σ bond	2e-	50% from C; 50% from C	C: 36.09%(s), 63.86%(p), 0.04%(d); C: 36.07%(s), 63.86%(p), 0.04%(d)
C-C (benzene) π bond	1.66e-	50% from C; 50% from C	C: 99.96%(p), 0.04%(d); C: 99.96%(p), 0.04%(d)
B-N (borazine) σ bond	2e-	75.74% from N; 24.26% from B	N: 38.91%(s), 61.06%(p), 0.03%(d); B: 31.70%(s), 68.17%(p), 0.14%(d)
B-N (borazine) π bond	1.82e-	88.44% from N; 11.56% from B	N: 100%(p); B: 99.65%(p), 0.35%(d)

Comparing the π bond occupancies in 1,2-azaborine, borazine and benzene, it is discovered that the π bond occupancy of 1,2-azaborine (1.78) is between that in benzene (1.66) and borazine (1.82). The π bond occupancy is the lowest in benzene, and we know that the electrons are delocalised in benzene. On the other hand, the π bond occupancy is the highest in borazine, and there is only some partial delocalisation of the lone pair of the N atom in the molecule. Therefore, it can be said that a lower π bond occupancy corresponds to a large degree of delocalisation while a higher π bond occupancy corresponds to a small degree of delocalisation in the molecule. Hence, for 1,2-azaborine, the delocalisation of π electrons is less than the one observed in benzene but more than the partial delocalisation in borazine. This proves the intermediate behaviour of 1,2-azaborine between benzene and borazine. Also, as the aromaticity is related to the delocalisation of electrons, it can be concluded that the 1,2-azaborine has substantial aromatic behaviour, which again puts the behaviour of 1,2-azaborine between that of benzene (aromatic) and borazine (non-aromatic).

Vibrations of 1,2-azaborine, Borazine and Benzene

The result of the vibrational frequency analysis of 1,2-azaborine is shown below. The assignment and form of the vibrations are labelled for some frequencies, and they are compared with the frequencies given in the literature. C₄H₆BN: DOI:10042/to-3819 , B₃N₃H₆ DOI:10042/to-3818 , C₆H₆: DOI:10042/to-3820

Selected Vibrations of 1,2-azaborine

Calculated Frequency (cm-1)	Intensity	Assignment	Form of Vibration	Experimental Value (cm-1)
587	62	Out of plane wagging		579
727	30	Out of plane wagging		715
831	19	Out of plane wagging and twisting		820
917	2	C-B stretch		-
918	51	Out of plane twisting		894
1127	11	In plane scissoring and rocking		1109
1185	2	In plane scissoring		1162
1236	8	In plane scissoring and rocking		1216
1261	2	B-N stretch		-
1383	13	In plane rocking		1350
1463	19	C-N stretch		1427
1488	32	In plane rocking and scissoring		1453
1572	77	C=C stretch		1533
1658	46	C=C stretch		1613
2618	180	B-H stretch		2525
3128	21	C-H stretch		3008
3158	26	C-H stretch		3027
3176	6	C-H stretch		-
3200	15	C-H stretch		-
3603	32	N-H stretch		3398

It is observed that the calculated frequencies are larger than the experimental values with the difference being quite small (10 cm^-1) at lower frequencies but becoming very big (200 cm^-1) at high frequencies. Some correction method needs to be done on the calculated frequencies, as Gaussian tend to overestimate the stretching frequencies and the higher frequency modes, to make the frequencies more realistic when compared to the experimental values. Some of the vibrational frequencies and intensities in benzene and borazine are given below.

Vibrational Frequencies of Benzene and Borazine

Molecule and Assignment	Frequency (cm-1)	Intensity
Benzene: C-H stretch	3180	44
Benzene: C-H stretch	3180	44
Benzene: C=C stretch	1513	9
Benzene: C=C stretch	1513	9
Borazine: N-H stretch	3630	43
Borazine: N-H stretch	3630	43
Borazine: B-H stretch	2611	294
Borazine: B-H stretch	2611	294
Borazine: B-N stretch	1484	477
Borazine: B-N stretch	1484	477

There are many frequencies with zero intensities in the IR spectra of benzene and borazine and this can be explained from the fact that both molecules are of high symmetry. The symmetric stretches in benzene and borazine do not cause a change in the overall dipole moment due to the cancelling out of dipole moments during these stretches, and this causes the symmetric stretches to be IR inactive and not observed in the IR spectra. There is only one C-H stretch peak in the IR spectrum of benzene but four peaks are observed for 1,2-azaborine. This is because all the four H atoms connected to the C atoms in 1,2-azaborine are not eqivalent to each other, and each of them will give a peak due to its own C-H stretch. The vibrational frequencies of these four C-H stretches in 1,2-azaborine are scattered around the frequency of the C-H stretch in benzene. The C=C stretches in 1,2-azaborine have much larger frequencies than the one in benzene, and there are two different C=C stretches instead of one as observed in benzene. This suggests that there are still two types of C=C present in 1,2-azaborine although there is some delocalisation of electrons in the molecule, unlike benzene, which only has 1 C=C stretching frequency due to the equivalent C atoms after delocalisation of electrons. Also, the C=C stretching frequencies in 1,2-azaborine are larger than the one in benzene because the C=C double bonds in 1,2-azaborine still have some double bond character (bond order nearer to 2) unlike the C=C bond in benzene which has a bond order of about 1.5 after the delocalisation of electrons.

The N-H stretching frequency is slightly smaller in 1,2-azaborine than the one in borazine, with only one N-H stretch possible for 1,2-azaborine. Borazine, on the other hand, have 2 types of asymmetric N-H stretches which are degenerate, as there are more H atoms on the N atoms in borazine. The calculated B-H stretching frequencies for 1,2-azaborine and borazine are surprisingly very close to each other, suggesting that the B-H environment in 1,2-azaborine is not that different than the one in borazine. However, the B-N stretch in 1,2-azaborine is much smaller than the one in borazine, and its intensity is also very small when compared to the one in borazine. This seems to suggest that the B-N bond in 1,2-azaborine are weaker than the one for borazine.

NMR Spectrum of 1,2-azaborine

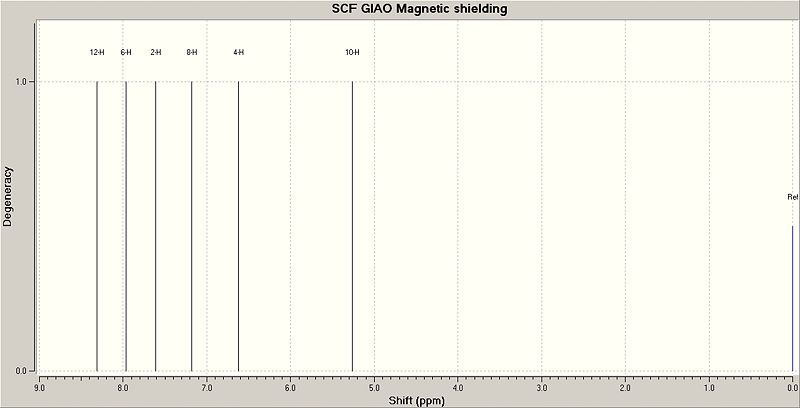
The structure of 1,2-azaborine is first optimised using the DFT: MPW1PW91 method with the 6-311G(d,p) basis set (DOI:10042/to-3840 before the ¹H NMR calculations are performed using the GIAO method (DOI:10042/to-3841 ). The calculated ¹H NMR chemical shifts are then compared with the experimental values given in the experiment in the table below.

Comparison of the Calculated and Experimental ¹H NMR Chemical Shifts

H Assignment	Calculated Chemical Shift (ppm)	Experimental Chemical Shift (ppm)
N - H	8.31	8.44
C(4) - H	7.97	7.70
C(6) - H	7.61	7.40
C(3) - H	7.18	6.92
C(5) - H	6.62	6.43
B - H	5.26	4.9

The calculated ¹H NMR chemical shifts are slightly larger than the experimental values except for the N-H, where the calculated chemical shift is slightly smaller than its experimental value. Overall, the calculated chemical shifts can be assumed to be a rough approximation of the real chemical shifts. Compared to the experimental chemical shifts in borazine (N-H: δ=5.63ppm, B-H: δ=4.4ppm), it is found that the calculated chemical shifts for the N-H and B-H are significantly shifted downfield, which is consistent with the observation in the literatrure. This means that the H atoms on the N and B atoms of 1,2-azaborine are different from the ones in borazine (different chemical environment). The ¹H chemical shifts for all the C-H in 1,2-azaborine are about in the right region with the experimental values. This range of chemical shifts for the C-H (6.5 - 8.0 ppm) in 1,2-azoborine suggests that these H atoms are quite aromatic as their chemical shift range is in that of an aromatic H. The predicted ¹H NMR spectrum is shown below.

Molecular Orbitals of 1,2-azaborine, Borazine and Benzene

The molecular orbitals of 1,2-azaborine, borazine and benzene are calculated using Gaussian. C₄H₆BN: DOI:10042/to-3819 , B₃N₃H₆ DOI:10042/to-3818 , C₆H₆: DOI:10042/to-3820 . The molecular orbitals with energies close to the Highest Occupied MO (HOMO) and Lowest Unoccupied MO (LUMO) of these three molecules are shown below.

Molecular Orbitals of 1,2-azaborine, Borazine and Benzene

Molecular Orbitals	1,2-azaborine	Borazine	Benzene
HOMO-2 (Molecular Orbital 19)
HOMO-1 (Molecular Orbital 20)
HOMO (Molecular Orbital 21)
LUMO (Molecular Orbital 22)
LUMO+1 (Molecular Orbital 23)
LUMO+2 (Molecular Orbital 24)

The HOMO-2 of 1,2-azaborine looks more like the HOMO-2 of borazine than benzene. The HOMO-2 of benzene looks more symmetrical, but this is not observed in the HOMO-2 of 1,2-azaborine. However, HOMO-2 of 1,2-azaborine has two small lobes that are in opposite phase with their neighbouring lobes at two of its ring bonds, just like benzene but not really observed in borazine. There is a lobe with high electron density on the H atom connected to B in both HOMO-2 of 1,2-azaborine and borazine. The HOMO-2 orbitals of these three molecules are mostly the antiboding σ* orbitals of the bonds that make up the ring structure.

The HOMO-1 of 1,2-azaborine, borazine and benzene are the π bonding orbitals (with 1 nodal plane) of the bonds that form the ring. The HOMO-1 of 1,2-azaborine is more similar to the one in benzene, as they seem to have some sort of symmetry, unlike the one in borazine which is totally unsymmetric. There is a higher density of electrons on the N atom of 1,2-azaborine than the B atom as there seems to be no lobe around the B atom.

For the HOMO of the three molecules, only the one for benzene shows symmetry, whereas the one for 1,2-azaborine and borazine do not show any symmetry. This causes the HOMO of 1,2-azaborine to be similar to that of borazine. The N atom of 1,2-azaborine seems to pull the lobe of the orbital towards itself, causing the lobe to be shifted more to one side. The HOMO is also the π bonding orbitals of the bonds that form the ring with 1 nodal plane.

The LUMO of 1,2-azaborine, borazine and benzene are the π* antibonding orbitals (with 2 nodal planes) of the bonds that form the ring. The one for 1,2-azaborine and borazine are not symmetrical but the one for benzene shows some symmetry properties. This means that the LUMO of 1,2-azaborine is more similar to the one in borazine than benzene, with both the LUMO of 1,2-azaborine and borazine having one N atom with a single orbital lobe on it.

The LUMO+1 of 1,2-azaborine, borazine and benzene are also the π* antibonding orbitals (with 2 nodal planes) of the bonds that form the ring. Only the LUMO+1 of benzene has symmetry properties, but the one for 1,2-azaborine looks like it could have some symmetrical properties. There is one very small orbital lobe (compared to the others) on one of the atoms in borazine but the one in 1,2-azaborine does not really show this difference in lobe size, causing the LUMO+1 of 1,2-azaborine to be more similar looking to the one in benzene than borazine.

The LUMO+2 of both borazine and benzene have symmerical properties with the one for benzene more symmetrical than borazine, which is expected as the structure of benzene shows more symmetry than borazine. Surprisingly, the LUMO+2 of 1,2-azaborine does not have any symmetry at all, and does not look like the one for borazine and benzene. The outer ring lobe (outside the H atoms) of LUMO+2 of 1,2-azoborine is disconnected, causing it to not cover the entire molecule, making it different from that in borazine and benzene. The inner lobe (green-coloured) is also disconnected. The only similarity between the LUMO+2 of 1,2-azaborine and borazine is the larger size of the outer ring lobe at positions outside the H atom which is connected to the N atom.

The calculated HOMO of 1,2-azaborine is consistent with the one given in literature. It is also worth nothing that there is no degenerate orbitals with the same energy level in 1,2-azaborine, which is very different from the case in benzene and borazine. Benzene has a lot of molecular orbitals with degenerate energy levels while borazine has a lot of molecular orbitals with an almost degenerate energy levels, but they can be considered as degenerate due to the very small difference in their energy levels (approximately 0.00001 a.u.).

Energy Levels of Selected MOs of 1,2-azaborine, Borazine and Benzene

Molecular Orbitals	Energy Level in 1,2-azaborine (a.u.)	Energy Level in Borazine (a.u.)	Energy Level in Benzene (a.u.)
LUMO+2	0.02931	0.04649	0.04234
LUMO+1	0.01127	0.01156	-0.00943
LUMO	-0.02918	0.01155	-0.00943
HOMO	-0.22995	-0.28501	-0.25637
HOMO+1	-0.28983	-0.28502	-0.25637
HOMO+2	-0.31603	-0.32906	-0.34765

From the table above, it is found that the LUMO of 1,2-azaborine is stabilised (negative energy level). For benzene, both the LUMO and LUMO+1 are stabilised but for borazine, none of the unoccupied orbitals is stabilised as all of them, including the LUMO has a positive energy level. This seems to suggest that a relationship exists between the aromaticity of the molecule and the stabilisation of the unoccupied orbitals. Benzene, which is aromatic, has two stabilised unoccupied orbitals (LUMO, LUMO+1) while borazine, which is not aromatic, has no stabilised unoccupied orbitals. 1,2-azaborine which has 1 stabilised unoccupied orbital, must have aromaticity which is between that of benzene and borazine, hence, it is said to have some aromatic behaviour.

The HOMO of 1,2-azaborine is not degenerate, which makes it different from benzene and borazine which have degenerate orbitals as their HOMO. In fact, the LUMOs of borazine and benzene are also degenerate. The HOMO-LUMO energy gaps in all three molecules are calculated with the following result: 1,2-azaborine = 5.5 eV, borazine = 8.1 eV, benzene = 6.7 eV. This shows that the energy gap in 1,2-azaborine is smaller than those for borazine and benzene, which is consistent with the trend given in literature (1,2-azaborine = 5.32 eV, borazine = 7.91 eV, benzene = 6.55 eV ). This also means that less energy is required to excite the 1,2-azaborine molecule to its first excited state than borazine and benzene.

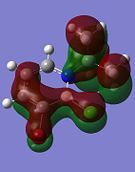
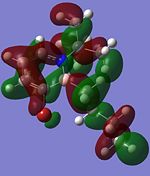
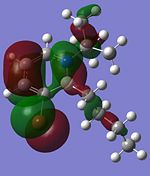
Since 1,2-azaborine is said to have some aromatic behaviour, this means that there is delocalisation of electrons in its structure and this is usually due to the π-type overlap of the p atomic orbitals of the atoms that form the ring, forming π-type molecular orbitals. The following orbitals are π-type MOs that could give rise to the delocalisation of electrons:

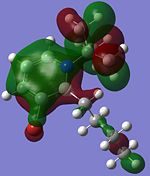
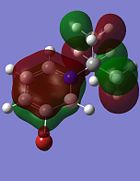
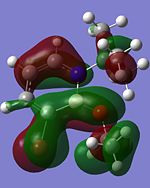
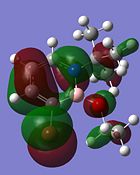
Other interesting molecular orbitals of 1,2-azaborine are shown below.

Molecular Orbital	Diagram	Comment
MO 7		This is from the constructive overlap between the orbitals of all the ring atoms. This can be said to be the σ bonding molecular orbital of the ring. The electron density and the lobe of the orbital is pulled towards the electronegative N atom.
MO 29		This is the completely π* antibonding molecular orbital where every p orbital on each ring atom is out of phase with each other. The p orbital of the N atom is very small, with a very small lobe, consistent with the fact that more electronegative atoms contribute more in the bonding orbitals and less in antibonding orbitals. The p orbital of the B atom is very large (large contribution from B) with a very large lobe which is large enough to interact with the p orbital from the C atom next to N.
MO 31		This is an unusual looking molecular orbital. It seems to consist of the s orbitals from the H atoms, the σ bonding orbitals of the ring and the π orbitals of the ring, with a large lobe outside of the H atom which is connected to B.

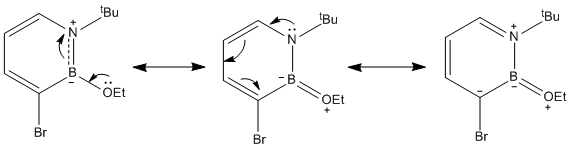
Formation of 1,2-azaborine Derivative

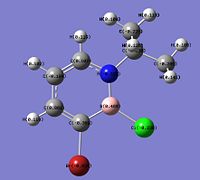
The reaction scheme shown below can be used to form a 1,2-azaborine derivative which can be used to react with nucleophiles. Compound 1 is first dehydrogenated to get compound 2 which has a tertiary butyl protecting group on the N atom and a Cl on the B atom. Compound 2 is then reacted with bromine in a electrophilic aromatic substitution reaction to get compound 3. The change in energy for each step of the reaction can be determined after the calculations of the energies of all the reactants and products involved in the two steps. The energies of compound 1, compound 2, H₂, Br₂, HBr and compound 3 are determined from the optimisation calculations, and checked with frequency analysis. (Compound 1:DOI:10042/to-3821 , Compound 2:DOI:10042/to-3822 , Compound 3:DOI:10042/to-3823 , H₂:DOI:10042/to-3827 , Br₂:DOI:10042/to-3826 , HBr:DOI:10042/to-3828 )

E(compound 1)= -853.89014419 a.u.

E(compound 2)= -852.69314076 a.u.

E(compound 3)= -3426.23435814 a.u.

E(H₂)= -1.17957105 a.u.

E(HBr)= -2574.75262977 a.u.

E(Br₂)= -5148.28402030 a.u.

The change in energy of the reaction is equal to the energies of the products minus the energies of the reactants. Therefore,

For Step 1: ΔE₁ = [E(compound 2) + E(H₂)] - E(compound 1) = 0.01743235 a.u. ≡ 46 kJ/mol

For Step 2: ΔE₂ = [E(compound 3) + E(HBr)] - [E(compound 2) + E(Br₂)] = -0.0098263 a.u. ≡ -26 kJ/mol

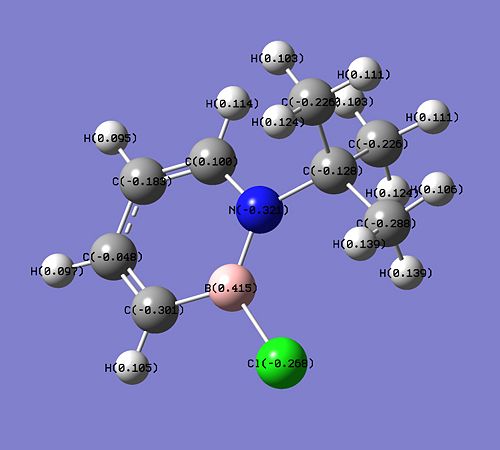
The ΔE₁ of step 1 is positive, suggesting that extra energy is required to drive the dehydrogenation reaction of compound 1. In fact, according to the literature , this step requires the usage of a catalyst, Pd/C and heating at 80°C for 16 hours. On the other hand, the ΔE₂ of the electrophilic aromatic substitution of compound 2 with Br₂ is negative, and this suggests that the reaction is favourable and does not need any extra energy to drive the reaction. The position of the substitution (at carbon of position 3) can be explained from the charge distribution of compound 2 (shown below).

The C atom at the 3 position has the highest negative charge (-0.301) than the other C atoms in compound 2 and this makes it reactive (electron-rich) and can react with Br₂ in an electrophilic substitution reaction. The only other atom to have a more negative charge is the N atom (-0.321) but the substitution cannot take place at this position as the N atom is protected by the bulky ^tBu group. It is also predicted than the electrophilic substitution reaction would happen more readily in compound 2 than in the parent 1,2-azaborine as the negative charge on the C atom at position 3 is higher in compound 2 (-0.301 vs -0.292). The presence of the negative charge on the C atom of position 3 makes the second reaction step very favourable.

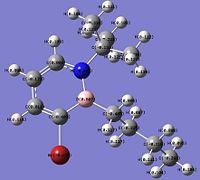
Reaction of 1,2-azaborine Derivative (Compound 3) with Nucleophiles

The charge distribution in compound 3, obtained from the optimisation calculation, is shown below. It is found that the B atom has a high positive charge (+0.489), higher than the ones in compound 2 (+0.415) and the parent 1,2-azaborine (+0.237). This makes the B atom in compound 3 very susceptible to nucleophilic attacks.

As the B atom is electron deficient (partially positive charged), nucleophilic substitutions at the B atom in compound 3 can occur readily as shown in the reaction below . For this computational experiment, some products of the nucleophilic substitution reaction are studied with the nucleophiles involved being ⁿBu^-, H^- and EtO^-.

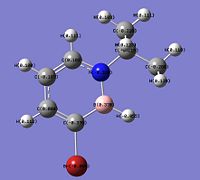
Structures of the Products

The four 1,2-azaborine derivatives studied are labelled compound 3 (Cl substituent on B), compound 4 (ⁿBu substituent on B), compound 5 (H on B) and compound 6 (OEt substituent on B). The optimised structures of these four derivatives, calculated by Gaussian are shown below; and these structures are checked using frequency analysis. The energies from the optimisation calculations match those from the frequency calculations, confirming that these structures are indeed the optimised structure. Optimisation: Compound 3:DOI:10042/to-3823 , Compound 4:DOI:10042/to-3833 , Compound 5:DOI:10042/to-3824 , Compound 6:DOI:10042/to-3834 . Frequency Analysis: Compound 3:DOI:10042/to-3831 , Compound 4:DOI:10042/to-3835 , Compound 5:DOI:10042/to-3832 , Compound 6:DOI:10042/to-3836 .

Optimised Structures of 1,2-Azaborine Derivatives

Compound 3	Compound 4	Compound 5	Compound 6
Compound 3	Compound 4	Compound 5	Compound 6

The bond lengths and bond angles in compounds 3, 4 and 6 are compared with the one in compound 5 as compound 5 is considered as the standard or parent molecule with the other compounds formed by substituting the H atom on the B of compound 5. Some of the bond lengths in the four compounds and the ring angles centred at the B and N atoms are given in the table below.

Comparison of Selected Bond Lengths and Bond Angles in Compounds 3, 4, 5 and 6

Parameter	Compound 3	Compound 4	Compound 5	Compound 6
C-Br Bond Length (Å)	1.92	1.94	1.93	1.94
C-B Bond Length (Å)	1.53	1.54	1.51	1.53
B-N Bond Length (Å)	1.45	1.47	1.44	1.48
C-N Bond Length (Å)	1.38	1.38	1.37	1.37
C-C Bond Lengths (C3 - C4, C4 - C5, C5 - C6) (Å)	1.36, 1.41, 1.36	1.36, 1.41, 1.36	1.37, 1.42, 1.37	1.36, 1.41, 1.36
C-B-N Bond Angle (°)	116.7	113.1	115.8	114.4
C-N-B Bond Angle (°)	117.4	119.4	119.7	119.7

The C-N and C-C bond lengths in all four compounds are about the same, suggesting that this part of the ring structure of 1,2-azaborine is not affected by the change of substituent at the B atom. The C-Br bond length does change with the change of substituent on the B atom. In compound 3 where the substituent is a single Cl atom, the C-Br bond becomes slightly shorter than the one in compound 4, but this bond length is observed to have increased slightly in compounds 4 and 6, where the substituents on the B atom are larger molecules (n-butyl and ethoxy group). The C-B bond length increases with any substituent on the B atom, as long as it is not H (compound 5). It seems that the larger the size of substituent group is, the longer the C-B bond will become. Compound 4, with a large n-butyl group, has the longest C-B bond length, while compound 5 with a small H atom, has the shortest C-B bond. The increase in the C-B bond length with the size of the substituent on B is probably due to the minimisation of steric repulsion between the large substituent at the B atom and the Br atom on the C atom next to the B. A longer C-B bond will help keep the large substituent further away from the Br, reducing the steric repulsion. The B-N bond length also increases when there is a substituent on the B atom. In fact, the increase in the B-N bond length is similar to the observed increase in the C-B bond length, except that compound 6 has the longest B-N bond instead of compound 4 which has the longest C-B bond. The reason for the increase of B-N bond length is probably to minimise steric repulsion between the substituent on B and the t-butyl substituent on the N atom.

The C-N-B bond angles for compounds 4, 5 and 6 are about the same while this angle is smaller in compound 3. There seems to be no direct relationship between the size of the substituent on the B atom and the C-N-B bond angle. For the C-B-N bond angle, the angle is larger for compounds 3 and 5, which have a single atom substituent on the B atom. This angle is smaller in compounds 4 and 6 which has a large substituent on the B atom. Again, there seems to be no clear relationship between the size of the substituent and the C-B-N bond angle. It is perhaps more accurate to describe the sizes of the C-B-N and C-N-B bond angles as dependent on the relative C-B and N-B bond lengths in the 1,2-azaborine derivatives. The bond lengths of C-B and N-B and bond angles of C-B-N and C-N-B are related to each other and they work in such a way to move the substituent on the B atom to a position where the steric repulsion with the Br atom and the t-butyl group is minimised.

Comparing the four 1,2-azaborine derivatives with the parent 1,2-azaborine, it is learnt that the structure of compound 5 is most similar to the structure of 1,2-azaborine. All the bond lengths between the ring atoms in compound 5 are exactly the same as the corresponding bond lengths in 1,2-azaborine, but the C-B-N and C-N-B bond angles are different. The C-B-N bond angle is slightly larger while the C-N-B bond angle is considerably smaller in compound 5 than 1,2-azaborine. The close similarity between the structures of compound 5 and 1,2-azaborine is quite unexpected (especially the bond lengths) as one would assume that the substitution of a Br atom at the C of position 3 and a t-butyl group on N would affect the structure of the ring significantly. However, compound 5 is indeed expected to be more similar to 1,2-azaborine than compounds 3, 4 and 6 as these other three compounds have three substituents on their ring whereas compound 5 only has two substituents.

Charge Distributions of the Products

The charge distributions of the atoms in compounds 3, 4, 5 and 6 are shown below. (Compound 3:DOI:10042/to-3831 , Compound 4:DOI:10042/to-3835 , Compound 5:DOI:10042/to-3832 , Compound 6:DOI:10042/to-3836 )

Charge Distribution of Compounds 3, 4, 5 and 6

Parameter	Compound 3	Compound 4	Compound 5	Compound 6
Diagram
Charge on N	-0.322	-0.342	-0.310	-0.374
Charge on B	+0.489	+0.607	+0.370	+0.620
Charge on C (position 3)	-0.369	-0.403	-0.370	-0.424
Charge on Br	-0.034	-0.079	-0.068	-0.080

It is found that the charge distribution on the B atom is most positive in compound 6. This is probably due to the substituent, -OEt which is connected directly to the B atom. The O atom is very electronegative, and it withdraws electron density from the B atom, causing the B atom of compound 6 to be very electron deficient and very susceptible to nucleophilic attack (most reactive in nucleophilic substitution). The charge on the N and C₃ is also the most negative for compound 6. This is beacuse the ethoxy group is a good electron-donating group due to the lone pair of electrons on the O atom which can be delocalised into the ring. The delocalisation of electron from O to the ring system will give structures where the electron density will be placed on the N (more negative than what it was) and C₃, causing these two atoms in compound 6 to have a higher negative charge density than the other compounds. As the C atom at the 3 position has the highest negative charge density in compound 6, compound 6 will also be the most reactive in the electrophilic aromatic substitution.

For compound 4, the n-butyl substituent can be considered as a weak electron-donating group. Less electron density is donated into the ring, causing the negative charge on the N and C₃ in compound 4 to be not as negative as the one in compound 6. For compound 3, its substituent, Cl is an electronegative and electron-withdrawing atom. The electronegative nature of Cl causes the B atom of compound 3 to have a higher positive charge than the one in compound 5. However, Cl is a very poor electron-donating atom, hence, the negative charge on B and C₃ in compound 3 is about the same as the one in compound 5.

NBO Analysis of the Products

The second order perturbation theory analysis results of the four compounds are examined to see if there is any important interactions from the bonding or filled lone pair orbitals into antibonding or empty orbitals. (Compound 3:DOI:10042/to-3831 , Compound 4:DOI:10042/to-3835 , Compound 5:DOI:10042/to-3832 , Compound 6:DOI:10042/to-3836 ). For all the four compounds, it is learnt that there is significant overlap from the N-B π bonding orbital into the C₅-C₆ π* antibonding orbital, from the C₅-C₆ π bonding orbital into the C₃-C₄ π* antibonding orbital, from the C₃-C₄ π bonding orbital into the C₅-C₆ π* antibonding orbital and from the C₃-C₄ π bonding orbital into the N-B π* antibonding orbital. Compounds 3 and 6 show an additional interaction each, with the overlap between the filled lone pair orbital on Cl into N-B π* antibonding orbital for compound 3 and the overlap between the filled lone pair orbital on O into N-B π* antibonding orbital for compound 6. For compounds 3, 4 and 5, the strongest interaction is the one between the N-B π bonding orbital and the C₅-C₆ π* antibonding orbital, while the strongest interaction for compound 6 is between the filled lone pair orbital on O and the N-B π* antibonding orbital. All thses interactions describe the delocalisation of electrons into and around the ring structure. The strong interaction between the lone pair of electrons on O and the N-B π* antibonding orbital in compound 6 is expected as we know that the ethoxy group is a very good electron-donating group. The surprising part is the presence of the interaction between the lone pair on Cl and the N-B π* antibonding orbital in compound 3, which is not expected as Cl is known as an electronegative atom which likes to hold on to its electrons strongly (non-electron-donating). However, this interaction between the lone pair on Cl and the N-B π* orbital is quite weak and not as strong as the one between the lone pair on O and the N-B π* orbital in compound 6.

The C-N, C-Br, C-B and B-N bond analysis results are shown in the table below.

Selected Bond Analysis in Compounds 3, 4, 5 and 6

Bonding	Compound 3	Compound 4	Compound 5	Compound 6
C-N	C: 37.16%; N: 62.84%	C: 37.42%; N: 62.58%	C: 37.32%; N: 62.68%	C: 37.48%; N: 62.52%
C-Br	C: 48.52%; Br: 51.48%	C: 46.88%; Br: 53.12%	C: 47.63%; Br: 52.37%	C: 46.85%; Br: 53.15%
C-B	C: 66.89%; B: 33.11%	C: 67.71%; B: 32.29%	C: 66.40%; B: 33.60%	C: 67.01%; B: 32.99%
B-N (σ)	B: 22.32%; N: 77.68%	B: 21.57%; N: 78.43%	B: 22.68%; N: 77.32%	B: 22.51%; N: 77.49%
B-N (π)	B: 15.38%; N: 84.62%	B: 13.72%; N: 86.28%	B: 14.87%; N: 85.13%	B: 12.02%; N: 87.98%

The C-N bond is about the same in all four compounds, indicating that the bond is not affected by the change of substituent on the B atom. An electron-donating substituent (compounds 4 and 6) will cause the C atom to contribute less to the C-Br bond while an electron-withdrawing substituent (compound 3) makes the C atom contribute more to the C-Br bonding. However, this change in the C atom contribution to the C-Br bond is very small. For the σ B-N bond, the B atom contribution to the bond remains about the same after the change of substituent on B for compounds 3 and 6. However, for compound 4, the B atom contribute slightly less to the σ B-N bond.

The C-B bond is slightly affected by the presence of substituent on the B atom. For compounds 3, 4 and 6, the C atom contributes slightly more to the C-B bond than it does in compound 5. This change in contribution from the C atom in the C-B bond could be related to the change in the difference in the charge distributions on the C₃ and B atoms. For compounds 3, 4 and 6, the difference in charge distributions between C₃ and Br is larger than the one in compound 5, and this could mean that there is more electronegativity difference between the C₃ and B atoms for compounds 3, 4 and 6. A larger electronegativity difference would mean that the more electronegative atom, which is C in this case, will contribute more to the bonding. Hence, the C atom contribute more in the C-B bond in conmpounds 3, 4 and 6.

For the π B-N bond, the contributions of the B and N atoms to the bonding change significantly with the change in substituent on the B atom. An electron-withdrawing substituent such as Cl (compound 3) seems to cause the B atom to contribute more to the B-N bond while the N atom will contribute less. The reason for this is unknown. On the other hand, a good electron-donating substituent such as ethoxy in compound 6, will result in the N atom contributing more to the B-N π bond. This could be due to the increase in electron density on N due to the donation of electrons from O into the ring. A more negatively charged N atom could result in the N atom contributing more to the B-N π bond as the N atom could be said to be more 'electronegative'. The n-butyl group is a weak electron-donating group, hence the N atom in compound 4 is not as negatively charged as the one in compound 6. This results in the smaller increase of the N atom contribution to the B-N π bond in compound 4, when compared to compound 6.

Vibrational Frequencies of the Products

The stretching frequencies of some common bonds in compounds 3, 4, 5 and 6 are listed in the table below. Compound 3:DOI:10042/to-3831 , Compound 4:DOI:10042/to-3835 , Compound 5:DOI:10042/to-3832 , Compound 6:DOI:10042/to-3836

Selected Vibrational Frequencies of Compounds 3, 4, 5 and 6

Vibration	Compound 3	Compound 4	Compound 5	Compound 6
C=C stretch	1657 cm-1, 1543 cm-1	1661 cm-1, 1544 cm-1	1649 cm-1, 1536 cm-1	1651 cm-1, 1542 cm-1
C-B	1366 cm-1	1372 cm-1	1378 cm-1	1384 cm-1
C-N	1310 cm-1	1307 cm-1	1314 cm-1	1322 cm-1
N-B	1184 cm-1	1180 cm-1	1234 cm-1	1142 cm-1
C-Br	707 cm-1	699 cm-1	724 cm-1	718 cm-1

The two C=C stretching frequencies of the four compounds are considerably close to each other and they are in the right IR spectroscopy region where C=C double bond peaks are found. All the C=C bonds in the four compounds are in an almost equivalent environment, and all of them still show some aromaticity as their peaks are in the same region where the C=C streching frequencies of 1,2-azaborine are found. The C-B stretching frequencies for these four compounds are quite different from each other, with compound 6 having the highest stretching frequency and compound 4 having the lowest frequency. It is also found that the C-B stretching frequencies of these four compounds are much higher than the one reported for 1,2-azaborine. This suggests that the presence of substituents on the C₃ and/or B atom in the structure can change the strength of the C-B bond, and shift its stretching frequency to a higher value.

Compounds 3, 4, 5 and 6 have a quite similar C-N stretching frequency but this value is different from the one reported in 1,2-azaborine. This again suggests that the presence of a substituent, in this case a t-butyl on the N atom, can change the strength of a chemical bond connected to the atom with the substituent. All the N-B stretching frquencies of compounds 3, 4, 5 and 6 are very different from one another, except for compounds 3 and 4 which have stretching frequencies which are quite close to each other. Compound 5 has the highest N-B stretching frequency, and this means that its N-B bond is the strongest among the four compounds. For compound 6, the lone pair of electrons on the O atom can overlap with the π* antibonding orbital of N-B (as shown in the NBO analysis result) and this weakens the N-B bond. As the N-B bond in compound 6 is weaker, its stretching frequency is lower than the other compounds, which is the result given by the frequency calculations. The C-Br stretching frequencies for all four compounds are relatively close to each other and they lie near the expected range of frequencies for the C-Br stretch on an aromatic system (above 690 cm^-1).

Molecular Orbitals of the Products

The total number of filled molecular orbitals in compounds 3, 4, 5 and 6 is different as there are different number of electrons present in the four structures due to the different substituents on the B atom. None of these four compounds has any degenerate molecular orbitals, which is expected as all the molecular orbitals in the parent 1,2-azaborine itself are non-degenerate. The relative energy levels of the LUMO+2, LUMO+1, LUMO, HOMO, HOMO-1 and HOMO-2 obtained from the Gaussian population analysis are given in the table below. MO: Compound 3:DOI:10042/to-3831 , Compound 4:DOI:10042/to-3835 , Compound 5:DOI:10042/to-3983 , Compound 6:DOI:10042/to-3984 .

Energy Levels of Selected Molecular Orbitals in Compounds 3, 4, 5 and 6

Energy Level	Compound 3	Compound 4	Compound 5	Compound 6
LUMO+2	-0.00141	0.00806	0.00664	0.02508
LUMO+1	-0.00226	0.00517	0.00033	0.00108
LUMO	-0.04910	-0.03755	-0.04013	-0.03196
HOMO	-0.22752	-0.21904	-0.22351	-0.20807
HOMO-1	-0.27188	-0.26828	-0.27071	-0.26586
HOMO-2	-0.27699	-0.27078	-0.27456	-0.27029

Comparing the energy levels of the molecular orbitals in each compound, it is discovered that the number of stabilised unoccupied orbitals is different for some compounds. For compounds 4, 5 and 6, only the LUMO is stabilised (negative energy level) while the other molecular orbitals above the LUMO are not stabilised and have positive energy levels. On the other hand, three unoccupied orbitals in compound 3 (LUMO, LUMO+1 and LUMO+2) are stabilised. The HOMOs and LUMOs of compounds 3, 4, 5 and 6 are shown below.

HOMO and LUMO of Compounds 3, 4, 5 and 6

Molecular Orbital	Compound 3	Compound 4	Compound 5	Compound 6
LUMO
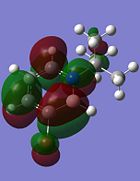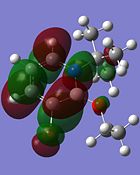
HOMO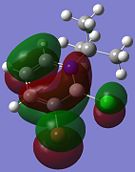

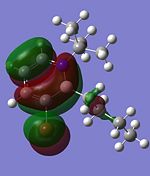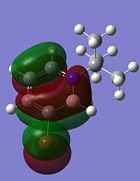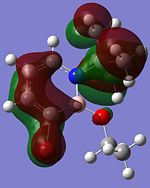
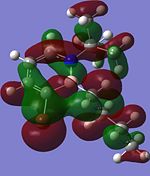
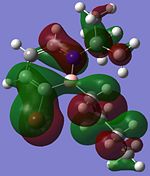
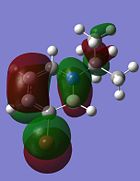
Although the substituents on the B atom are different for the four compounds, their HOMOs and LUMOs are about the same, especially the orbitals around the ring structure and they show some delocalisation of electrons around the ring structure, which gives some aromaticity to the four compounds. Other molecular orbitals which show some delocalisation of electrons around the ring (besides the HOMO and LUMO) are shown in the table below. These molecular orbitals can give some aromatic behaviour to compounds 3, 4, 5 and 6 due to the delocalised electrons in the ring structure.

Selected Molecular Orbitals of Compounds 3, 4, 5 and 6

Compound 3	Compound 4	Compound 5	Compound 6
		-

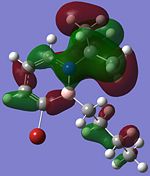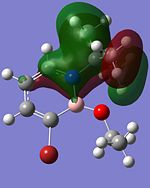
Comparing the molecular orbitals shown above, it is found that some of the molecular orbitals in the four compounds are about the same, with the only difference being the contribution from the different substituents on the B atom. These molecular orbitals prove one thing, that there is indeed delocalisation of electrons around the ring structure, just like the one observed in the parent 1,2-azaborine.

Conclusion

From all the analysis done, it can be concluded that 1,2-azaborine is indeeed an intermediate structure between benzene and borazine with some of its properties between that of benzene and borazine. 1,2-azaborine shows some aromatic behaviour due the delocalisation of electrons in the ring structure, including the partial delocalisation of the lone pair of electron on the N atom into the BN bond. The presence of positive charge on the B atom enables 1,2-azaborine to react in nucleophilic substitutions on the B atom while the high negative charge on the C₃ allows electophilic aromatic substitution to take place on the C₃ of 1,2-azaborine. Derivatives of 1,2-azaborine, such as compounds 3, 4, 5 and 6 also show similar substantial aromaticity behaviour like 1,2-azaborine but the relative aromaticity behaviour of each compound when compared to 1,2-azaborine is unknown and more analysis are required to determine this.