Rep:Mod:klw14

Optimizing the NH₃ Molecule, Frequency and NBO Charge

Optimisation

Method : B3LYP

Basis Set : 6-31G(d,p)

Results

Final Energy a.u. : -56.55776863

R.M.S Gradient : 0.00000478

Point Group : C_3V

N-H Bond Distance : 1.01797 Å

H-N-H Bond Angle : 105.743 °

         Item               Value     Threshold  Converged?
 Maximum Force            0.000004     0.000450     YES
 RMS     Force            0.000004     0.000300     YES
 Maximum Displacement     0.000071     0.001800     YES
 RMS     Displacement     0.000034     0.001200     YES

NH

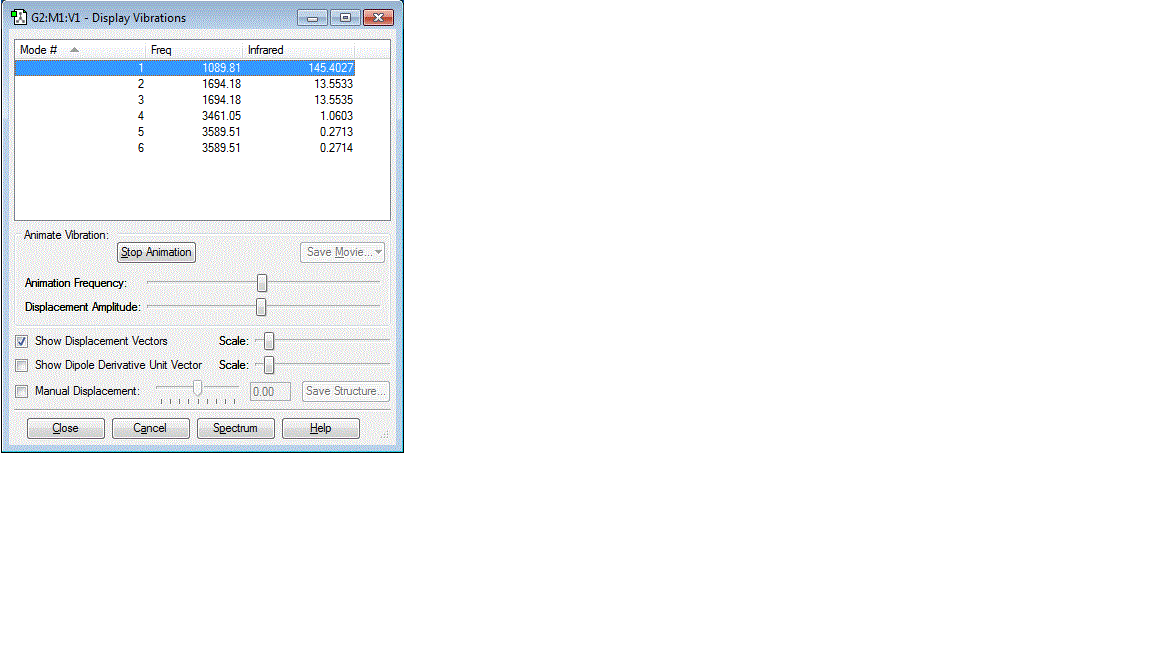
Frequency Analysis

Using the 3N-6 rule for the expected number of vibrational modes

3*4-6=6

The number of computed vibrational modes is also 6. There are 2 sets of degenerate vibraitonal modes. One being with vibraitons of about 1695 cm^-1 and those with vibrations at about 3590 cm^-1 The bending modes of the molecule are those that occur at lower frequency, 1090 cm^-1 and the degenerate modes at 1695 cm^-1. The bond stretching modes are higher frequency, occuring at 3460 cm^-1 and 3590 cm^-1. The vibrational mode at 3460 cm^-1 is the highly symmetric stretching mode and the vibration at 1090 cm^-1 is the highly symmetric bending mode, sometimes referred to as the umbrella mode.

In an experimental gaseous vibrational spectra, 2 peaks would be expected. The vibration at 1090 cm^-1 and the degenerate peaks at 1695 cm^-1 will combine to give a single peak.

NBO Charge Analysis

N Charge = -1.125 H Charge = +0.375

As the nitrogen is more electronegative it is able to pull the electron density away from the Hydrogen atoms, leaving H atoms slightly positive and the Nitrogen with a negative charge.

The Haber-Bosch Procsee

To determine the most stable gasoues species within the Haber-Bosch process the reactants need to be calculated.

H₂

The computational details are the same as those discussed for the NH₃ molecule, so wont be repeated here.

Results

Final energy a.u. : -1.17853934

R.M.S. gradient : 0.00000017

Point Group :D_infH

H-H bond Distance

    Item               Value     Threshold  Converged?
 Maximum Force            0.000000     0.000450     YES
 RMS     Force            0.000000     0.000300     YES
 Maximum Displacement     0.000000     0.001800     YES
 RMS     Displacement     0.000001     0.001200     YES

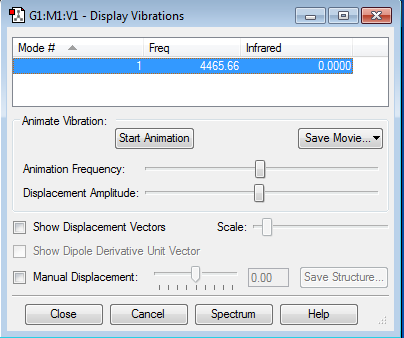
Frequency Analysis

This vibrational mode should not be visible in the gas phase IR.

NBO Charge Analysis

As the H₂ is a homo-diatomic molecule there is no change in electron distribution to affect the charges on the Hydrogen atoms.

N₂

The optimisation method and basis set is the same as for the NH₃ and the H₂ molecules.

Optimisation Results

Final energy a.u. : -109.52412907

R.M.S. gradient : 0.00000059

Point Group :D_infH

N-N bond distance

    Item               Value     Threshold  Converged?
 Maximum Force            0.000001     0.000450     YES
 RMS     Force            0.000001     0.000300     YES
 Maximum Displacement     0.000000     0.001800     YES
 RMS     Displacement     0.000000     0.001200     YES

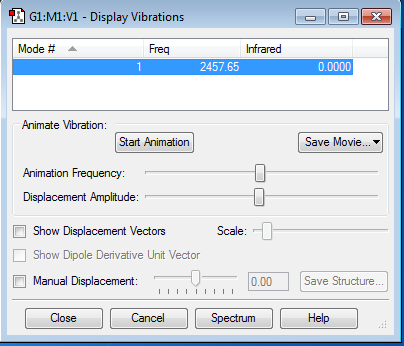
Frequency and NBO Charge Analysis

As was the case with Hydrogen, as this is a homo-diatomic molecule the vibrational mode will not appear in the gas phase IR spectra. The charge of the ions will also not change.

Calculating Energy for the Reaction

N₂ + 3H₂ --> 2NH₃

All energy values in a.u.

E(NH₃)= -56.55776863

2*E(NH₃)= -113.11553726

E(N₂)= -109.52412907

E(H₂)= -1.17853934

3*E(H₂)= -3.53561802

ΔE=2*E(NH₃)-[E(N₂)+3*E(H₂)= -0.05579017

The ΔE value in kJ/mol is -140.89

As the ΔE value is negative, this shows that the products of the reaction (NH₃) is the most stable species in the reaction.