Rep:Mod:kl1713TS

Transition States and Reactivity

Introduction

Figure 1: The Cope Rearrangement of 1,5 hexadiene

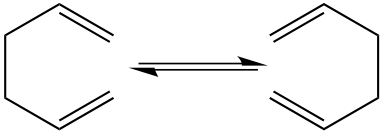
The Cope Rearrangement is a thoroughly studied pericyclic reaction involving a [3,3]-sigmatropic rearrangement of 1,5 dienes. In this report 1,5 hexadiene will be the molecule that will be investigated. 1,5 hexadiene is a symmetrical molecule as shown in Figure 1, therefore it may seem as though no reaction has taken place. However under heating of 1,5 hexadiene it is observed that the concerted rearrangement does occur and goes through a transition state. The idea that the mechanism is a concerted one has been discussed for many years, however, it is now believed to go via a concerted mechanism, this should become clear through this computational experiment.

The transition state is the main focus of this study. For the Cope Rearrangement the transition state can be in a 'chair' or 'boat' conformation. This computational experiment that will be carried out will be to optimize this transition state, and therefore understand why a reaction may prefer one conformation over another. The computation will be carried out using Gaussian + GaussView. A molecule of 1,5 hexadiene with both anti-periplanar (anti) and synclinal (gauche) linkages will be examined. The difference in these conformations is simply the dihedral angle of the central four carbons being rotated by 120°. From literature the anti-conformation is meant to be the most stable by a few kJ mol^-1 relative to the gauche conformation.

Chair structures can take different forms when rotating the dihedral angle. An anti chair structure is most stable due to it having the most favourable orbital interactions. The CH₂CH₂ substituents in the anti conformation are 180° to each other, and hence have no unfavourable interactions. Contrastingly, in the gauche structure where there has been a 60° rotation to the dihedral, it gives rise to 1,3 diaxial interactions which are unfavourable as the CH₂CH₂ groups clash.

Optimization of 1,5-Hexadiene conformers

Optimization of anti conformer

Molecular mechanics calculations were performed using Gaussian 09W and GaussView 5.0. The first step involved drawing an anti conformation of 1,5 hexadiene which will be cleaned and then optimized. In order to ensure the molecule was in an anti periplanar conformation the dihedral angle had to be modified to 180°. An additional requirement was the symmetry of the molecule, and this had to be set using the symmetrize function on GaussView. The level of theory used for this calculation was HF/3-21G.

Optimization log file can be found here

Nf710 (talk) 11:59, 5 November 2015 (UTC) you are not doing molecular mechanics, you are not appling a force field to anything. you are doing HF calculations

Table 1: Summary of anti 1,5 hexadiene conformer

Conformer	Optimized Structure	Results Summary	Point Group	Energy/Hartrees HF/3-21G
Anti	Anti HF/3-21G		C1	-231.69260

The optimized structure can be viewed in Table 1 with the energy recorded. Additionally, the symmetry of the molecule is observed to be C₁ indicating no high order of symmetry.

Optimization of gauche conformer

Following the previous computation, the same process is carried out, however this time drawing a gauche linkage for the central 4 carbon atoms. In order to do this as mentioned in the introduction it requires a 60° dihedral angle. This structure is expected to be higher in energy by a few kJ mol^-1 as mentioned in the introduction.

Optimization log file can be found here

Table 2: Summary of gauche 1,5 hexadiene conformer

Conformer	Optimized Structure	Results Summary	Point Group	Energy/Hartrees HF/3-21G
Gauche	Gauche HF/3-21G		C2	-231.69254

As expected, from the energies found through computation it is observed that the Gauche form is higher in energy by 3.06225 kcal mol^-1. The reasons for it being higher in energy have been explained in the Cope Rearrangement section of this report.

Nf710 (talk) 12:04, 5 November 2015 (UTC) you have only referenced literature, you haven't said that it is due to secondary orbital interactions, you could have even shown this if you had looked at orbitals in the .chk file.

Optimization of anti2 conformer

Finally, the anti2 1,5 hexadiene conformer was analysed using the same technique. The molecule was drawn by reffering to an image on 1,5 hexadiene in the anti2 conformation. Once again the molecule was optimized to a minimum using HF\3-21G.

Optimization log file can be found here

Table 3: Summary of anti2 1,5 hexadiene conformer

Conformer	Optimized Structure	Results Summary	Point Group	Energy/Hartrees HF/3-21G
Anti2	Anti2 HF/3-21G		Ci	-231.69260

The energy difference of anti and anti2 is minimal of 0.037651 kcal mol^-1. From this small difference it can be assumed that the conformers are the same despite having different point groups.

Reoptimization of anti2 conformer

Once confirming the anti2 conformer was optimized, it was then re-optimized using a higher level of theory of B3YLP/6-31G(d). Optimization log file can be found here

Table 4: Summary of 1,5 hexadiene computations anti2 at B3LYP/6-31G(d)

Conformer	Optimized Structure	Results Summary	Point Group	Energy/Hartrees HF/3-21G
Anti2	Anti2 HF/3-21G		Ci	-231.69254

Nf710 (talk) 12:09, 5 November 2015 (UTC)I think you have put the wrong data in here DFT should be around -234

DFT is a higher level of theory due to it being a more expensive but produces more accurate results. Density functional theory takes into account an extra term in its hamiltonion operator which takes into account the exchange - correlation potential due to spin and charge, as well as the basic terms such as kinetic energy of electrons, electron-nuclei interation and coloumb interaction between electron clouds. In the self-consistent field method - Hartree Fock, it runs by using the basic terms mentioned, however it does not take into account the electron correlation due to spin and charge. Hence, why the results show changes in the geometry of the molecule. Additionally, energies are largely different however they cannot be compared due to each level of theory using different approximations and therefore having a different zero point and so the scaling cannot be compared.

Comparing levels of theory

The two theories used in this computation are HF/3-21G and B3YLP/6-31G(d). As explained earlier they both take into account different approximations with the more expensive method being the latter DFT method. The molecule used for comparison is the anti2 molecule.

Table 5: Comparison of using different basis sets for anti2 bond lengths

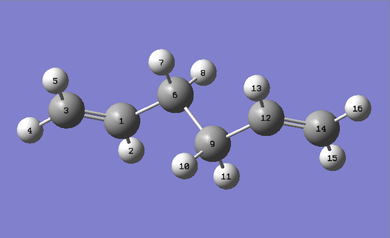
Atoms	HF/3-21G/(Å)	B3YLP/6-31G(d)/(Å)
C1-C3	1.31618	1.33350
C1-C6	1.50882	1.50420
C6-C9	1.55317	1.54816

The image of the molecule shows the labelling of each carbon and hydrogen atom. The table shows a comparison of the bond lengths of the two levels of theory. When using the DFT method the C1-C3 bond length has a distinct increase, C1-C6 is slightly shorter and C6-C9 is also shorter. The bond lengths obtained with the higher level of theory are more comparable to literature values. Using this level of theory is not entirely necessary for simple molecules such as 1,5 hexadiene, however, if a simple molecule such as this can have such a distinct difference in atoms C1-C3, corresponding to a C=C bond then a more complicated molecule with high order bonding will require a more expensive method for reliable results.

Table 6: Comparison of using different basis sets for anti2 dihedral angles

Atoms	HF/3-21G/(°)	B3YLP/6-31G(d)/(°)
C3-C1-C6-C9	114.62608	118.59950
C1-C6-C9-C12	180.00000	-180.00000
C6-C9-C12-C14	-114.62608	-118.59950

Analysis of the dihedral angles also shows distinct differences in the angles between the two different methods. The angles when using the DFT method increase by approximately 4°.

Nf710 (talk) 12:14, 5 November 2015 (UTC)You must have done the optimization because you have the correct results. Good comparisopn and good undertsanding.

Analysis of thermochemistry

Frequency Analysis

In this section the anti2 molecule which had been optimized to B3YLP/6-31G(d) will be analysed through a frequency analysis. This will yield information about structure to confirm whether there are any imaginary frequencies present. The Infrared Spectrum is also recorded and compared to actual data. Optimization log file can be found here

Table 7: Results from frequency analysis of anti2 B3YLP/6-31G(d)

Conformer	Results Summary	IR Spectrum
Anti2

From analysis of the log file produced by the frequency calculation the vibrations found are all real and positive, this confirms that the molecule has been successfully optimized to a minimum. If it were not at a minimum there would be a presence of imaginary frequencies which will be observed later when optimizing transition states. The frequencies which are obtained are calculated through the second derivates of energy. A hessian matrix will give eigenvalues and eigenvectors along its diagonal. A negative eigenvalue means that its harmonic frequency contains an imaginary number. Therefore, when an imaginary frequency is observed the geometry is at an energy maximum on the saddle point.

Nf710 (talk) 12:19, 5 November 2015 (UTC) this is a good understanding much further above what you need to expect, simply the second derivative of the energy is the force constant for that degree of freedom. This is then used to get the vibrational frequency from the vibronic harmonic oscillator equation. which has a root k term. therefore a negative k would give an imaginary frequency.

• Sum of electronic and zero-point Energies= -234.469219 Hartrees
• Sum of electronic and thermal Energies= -234.461869 Hartrees
• Sum of electronic and thermal Enthalpies= -234.460925 Hartrees
• Sum of electronic and thermal Free Energies= -234.500809 Hartrees

The above information can be explained. The sum of electronic and zero point energies (E = E_elec + ZPE) gives a value

The second is the sum of electronic and thermal energies which includes the translational, rotational, and vibrational energy modes at 298.15K (E = E + E_vib + E_rot + E_trans). Next is the sum of electronic and thermal enthalpies which includes an additional term of RT (H = E + RT). Finally, the sum of electronic and thermal free energies which include the entropic contribution (S) to the gibbs free energy (G), (G = H - TS).

Optimizing the "Chair" and "Boat" transition structures

In this section of the report three different methods will be used to optimize the 'chair' and 'boat' transition structures. The level of theory used for each method will be HF/3-21G. The first method used will optimize the chair using TS Berny, the second will optimize the chair by freezing co-ordinates, and the final method will optimize the boat structure to a transition state using the QST2 method.

Optimizing the allyl fragment

To begin this part of the computation an allyl fragment of CH₂CHCH₂ was drawn and optimized to a minimum using HF/3-21G. Optimization log file can be found here

Table 8: Summary of allyl fragment computation

Conformer	Optimized Structure	Results Summary	Point Group	Energy/Hartrees HF/3-21G
Allyl Fragment	Allyl fragment HF/3-21G		C2v	-115.82304

Optimizing to transition state using HF/3-21G (TS Berny)

Using the optimized allyl fragment it will be duplicated and then optimized to a chair transition state. This can be done on guassian by setting up the calculation to run and optimization and a frequency, optimize to a transition state (Berny), and then to calculate the force constants once. In addition to this extra keywords will be used, 'opt=noeigen'. This is used to ensure that the calculation will not break down if many imaginary frequencies are present. Before running the calculation it is important to make sure the allyl fragment has the correct C_i symmetry. Optimization log file can be found here

Table 9: Results of the transition state optimisation using TS Berny

Optimized structure	Results Summary	IR Spectrum	Energy/Hartrees HF/3-21G
Chair TS using TS Berny			-231.61932

The above table shows the information obtained from the log file of the opt+freq. In order to confirm it is a transition state, as explained earlier, it must have an imaginary frequency. When analyzing the log file a negative frequency of -817.96 cm^-1 was observed. Hence, confirming it is a transition state. The animation showing this vibration is shown below.

Imaginary frequency confirming it is a transition structure

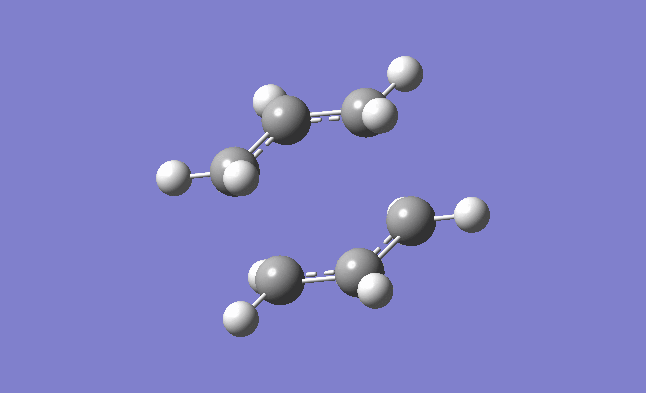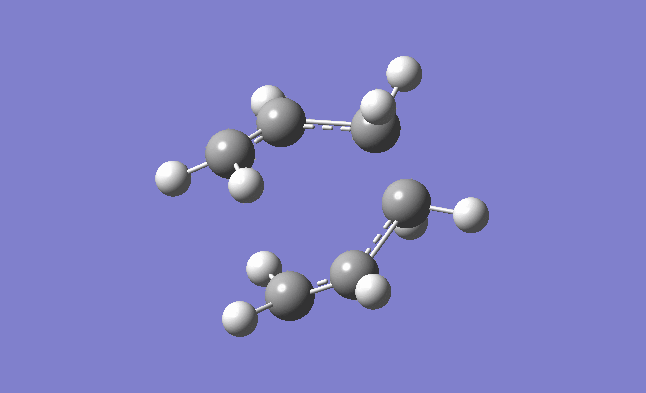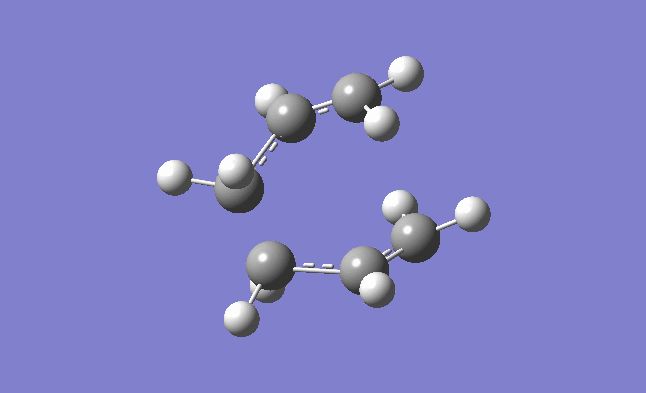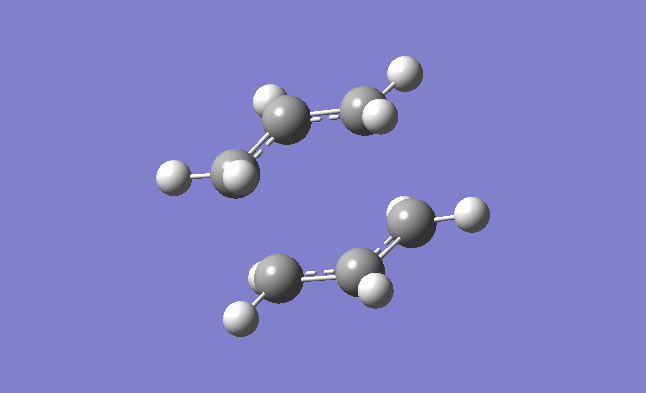
Optimizing to transition state using the Redundant Co-ordinate Editor (frozen co-ordinates)

This method will require the use of the redundant co-ordinate editor. Using the input file for the TS Berny calculation containing the optimized allyl fragment the co-ordinates of the terminal ends of the fragments will be frozen. The first step of the calculation requires the terminal carbons to be frozen to 2.20Å apart. A calculation is then run to optimize the molecule to a minimum, once again, at the HF/3-21G level. By freezing the co-ordinates the rest of the molecule is optimized to a minimum whilst leaving the terminal carbon ends of each fragment 2.20Å apart. In the second step, the terminal ends of each fragment which has not been optimized will now be optimized whilst ensuring the rest of the molecule is frozen. In the second step the calculation is set up to make sure it is optimized to a transition state and the force constants are not calculated.

Optimization log file can be found here

Table 10: Results of the transition state optimisation using frozen co-ordinates

Optimized structure	Results Summary	Energy/Hartrees HF/3-21G
Chair TS using frozen co-ordinates method		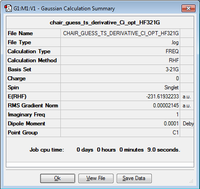-231.61932

Upon analysis of the log file the vibrations show one imaginary frequency at -817.89cm^-1, therefore confirming it is a transition state.

Comparison of using TS Berny and Frozen Co-ordinates Method

Both methods gave a transition state which was confirmed by the presence of a negative frequency. The first method gave a frequency of -817.96 cm^-1 and the second -817.89cm^-1 . These frequencies are very similar and hence both methods seem to work well to optimize to a transition state. In addition, the results summary shows that both methods give the same energy to 5 decimal places, and in reality these energies are only accurate to 1 decimal place due to all the approximations which take place for the calculation to proceed. Therefore, it can be said that both output structures are chair transition states, and both methods yield very similar results.

Table 11: Comparison of using different methods to optimize to a transition state

Atoms	TS Berny/(Å)	Frozen Co-ordinate/(Å)
C3-C14	2.02023	2.02023
C6-C11	2.02073	2.02076

Comparing the geometries of both methods shows that there is very slight difference between the bond lengths of the terminal carbons on each fragment. For that reason for a simple molecule such as the one being analysed both methods are as good as each other.

Nf710 (talk) 12:25, 5 November 2015 (UTC) Good comparisons, you have the correct frequencies.

Optimizing the boat transition structure

The third method used in order to optimize the structure to a transition state was the QST2 method. In contrast to the previous computations, this time a boat transition structure will be optimized. The key advantage of this method is that the whole process is automated, it works by providing the input file with a guess transition structure. If the transition structure is reasonably close to the actual transition structure then the whole process will be automated, and Gaussian will output the optimized transition state.

To begin the calculation the previously optimized C_i reactant molecule is used. This is then copied into a new window. This will be the reactant molecule. The same reactant molecule will then be copied again into the new window, but this time it needs to be in a new window next to the reactant molecule. This will now be the product molecule, as shown in the image below.

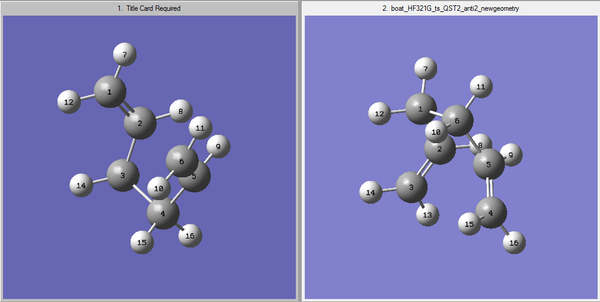
The most important part of the QST2 method is the labeling. It is vital that the labeling in the reactant structure matches with the labeling in the product structure, if it does not Gaussian will not be able to interpolate between the two structures. In addition to the labeling as mentioned before the guess structure needs to be similar to the real transition structure, therefore to give the structure boat conformation dihedral angles were modified. For both the reactant (left) and product (right) C2-C3-C4-C5 atoms dihedral angles were changed to 0°. Additionally, the angle between C2-C3-C4 and C3-C4-C5 were modified to 100°. This resulted in a structure which shows resemblance to the boat conformation. The above structure shows the boat conformation with matching labeling in both structures. Finally the calculation was set up to run an opt+freq. In the first method the optimization was selected to optimize to TS Berny, this time it optimizes to QST2. Once again using HF/3-21G.

Optimization log file can be found  here  

Table 12: Results for optimized boat transition structure using QST2

Optimized structure	Results Summary	Energy/Hartrees HF/3-21G
Optimized boat transition structure		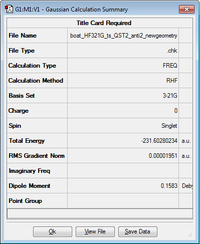-231.60280

In order to confirm the structure obtained is a transition structure, it must have an imaginary frequency. This was found to be present at -839.98 cm^-1. The vibration corresponding to this frequency is shown below.

Imaginary frequency for boat transition structure

Intrinsic Reaction Co-ordinate (IRC)

An intrinsic reaction co-ordinate is a way of gaining the reaction pathway from the transition structure. The idea is that the computation begins at the transition structure which is at a local maximum and it then slides down the hill on a trajectory of steepest decent until it reaches a local minimum. The calculation runs a sequence of constrained optimizations until a minima adjacent to the transition state is located. The number of optimizations can be set and in this computation 75 steps will be used. An IRC can be run in both the forwards and backwards directions as when you are at a transition state (maximum) you can descend either side. However, for a symmetrical reaction co-ordinate it is only necessary to run it in one direction.

The calculation was set up to run an IRC in both directions, whilst calculation force constants always, which is the first derivative of the gradient. Number of steps = 75. The level of theory was HF/3-21G. Optimization log file can be found here

Reaction co-ordinate	IRC for 75 points

The graph shows the reaction pathway in both directions. Analyzing the 'Total Energy along IRC' graph shows how in both the forward and backwards directions the calculation begins from the transition state (maximum) and keeps going until a local minimum is found. In addition, both directions were calculated to show how the reaction co-ordinate is symmetrical, and therefore for future calculations only one direction is necessary. The graph showing the gradient is also consistent with theory as it begins from a point where the gradient is 0 (maximum), it then runs along the trajectory of steepest decent until it reaches a minimum which tends to a gradient of 0.

Nf710 (talk) 12:28, 5 November 2015 (UTC) This is very nice, you have shown the complete reaction.

Activation Energies

In this section the activation energies for both the chair and boat structures will be calculated. In order to do this both structures will need to be reoptimized and a frequency run at a higher level of theory, using the DFT method, B3LYP/6-31G(d). The structures used will be the previously optimized HF/3-21G chair and boat structures. Additionally to these structures the reactant allyl fragment will also be reoptimized to B3LYP/6-31G(d). This is because to calculate activation energies it will be the energy of the transition state - the energy of the reactants.

Table 13: Summary of energies for chair, boat and anti2 (Hartree)

	HF/3-21G			B3LYP/6-31G(d)
	Electronic energy	Sum of electronic and zero-point energies	Sum of electronic and thermal energies	Electronic energy	Sum of electronic and zero-point energies	Sum of electronic and thermal energies
		at 0 K	at 298.15 K		at 0 K	at 298.15 K
Chair TS	-231.619322	-231.466699	-231.461346	-234.556926	-234.414919	-234.408988
Boat TS	-231.602802	-231.450929	-231.445300	-234.543093	-234.402356	-234.395068
Reactant (anti2)	-231.692535	-231.539539	-231.532566	-234.611711	-234.469219	-234.461869

The above table shows the energies obtained from the log file of the corresponding computations. An opt+freq had to be run in order to access this thermochemical data from the log file. In the table below activation energies have been calculated using the electronic energy.

Table 14: Summary of activation energies (in kcal mol^-1)

	HF/3-21G	HF/3-21G	B3LYP/6-31G*	B3LYP/6-31G*	Expt.
	at 0 K	at 298.15 K	at 0 K	at 298.15 K	at 0 K
ΔE (Chair)	45.71	45.94	34.07	34.38	33.5 ± 0.5
ΔE (Boat)	55.60	56.31	41.96	43.06	44.7 ± 2.0

The table above has the activation energies in kcal mol^-1. Analysing the table it is clear that the computation run at the higher, more expensive level of theory is closer to the experimental value. The HF/3-21G computation shows a larger discrepancy from the actual values for the activation energy. Furthermore, from all computations it can be observed that the chair transition state has a lower electronic energy than the boat transition state. For that reason when the reaction occurs, it is most likely to follow through the chair transition state pathway.

Nf710 (talk) 12:34, 5 November 2015 (UTC) You haven't shown the imagery frequencies of the of the optimised TS and furthermore you haven't shown the geometries. Therefore you haven't deduced that geometries tend to not change that much from a small basis set to a large one. where as energy is much more important. In all you have shown a very good understanding of the theory behind this work especially for the optimisations.

The Diels Alder Cycloaddition

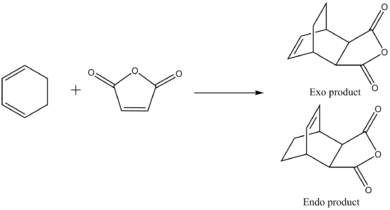
In this part of the computation the Diels Alder Cycloaddition will be discussed. Like the Cope Rearrangement it is also a concerted pericyclic reaction.In the reaction two conjugated π systems react with each other to form a ring and two new σ bonds. The reaction has two reactants, the diene and the dienophile, it is important that there is an electron rich diene and an electron poor dienophile. This is because for the reaction there needs to be a low lying LUMO and a high lying HOMO so that they are close in energy and lead to a good orbital interaction; the smaller the energy gap the better the orbital interaction. In addition to this criteria, the orbitals must have the same symmetry properties, if they are different the reaction is forbidden. This can be explained by the Woodward-Hoffmann Rules.

Woodward Hoffmann rules state that in a thermal pericyclic reaction the total number of (4q + 2)_s and (4r)_a components must be odd. The letters 'q' and 'r' represent any positive integer (1,2,3...) does not include 0. The suffixes 's' and 'a' descriptions of topology standing for suprafacial and antarafacial respectively.

The reaction which will be discussed for this computation will be between maleic anhydride (electron poor dienophile) and cyclohexadiene (electron rich diene). This normal demand reaction should proceed well due to the potentially good orbital interactions of the HOMO and LUMO. From this point onwards the exercise will compute calculations at the AM1 semi-empirical molecular orbital method. The reason for using this method is because a method HF without any approximations would be expensive and have computing time. AM1 uses NDDO (neglect of differential diatomic overlap) and this replaces the HF secular equation with something less complex. The method tries to replace many of the calculations a HF would do from scratch with pre-calculated experimental data (empirical) which are part of the integral. This makes calculations fast even for complex molecules, however, AM1 is only accurate for organic molecules, if an inorganic molecule was to be tested, such as, the presence of a transition metal a more accurate method such as PM5 should be used.

(A fairly good introduction to AM1 and its advantages. PM6 can be applied to a greater set of systems because, besides other reasons, it is more heavily parameterised. These methods are very useful for quickly generating "guess" structures before applying a computationally more expensive method such as B3LYP Tam10 (talk) 12:00, 28 October 2015 (UTC))

Optimization of cis butadiene + ethene

Using GaussView a structure of butadiene was drawn in cis orientation. To give it a cis orientation the dihedral angle had to be changed to 0°. Optimization log file can be found here

Table 15: Results summary for optimization of cis butadiene

Optimized structure	Results Summary	Point Group	Energy/Hartrees HF/3-21G
Optimized cis butadiene		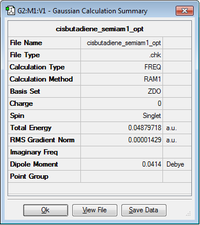C2v	0.048797

The above table shows the results of the cis butadiene optimization. From this optimization the molecular orbitals can be analysed and the HOMO and LUMO orbitals are shown below.

Molecular orbitals for cis butadiene

HOMO for cis butadiene	LUMO for cis butadiene

From the orbitals it can be seen that the LUMO is symmetric with respect to the plane whilst the HOMO is antisymmetric.

Optimizing ethene and computing the transition structure

In this part a molecule of ethene is draw on Gaussian and optimized to the AM1 semi-empirical method. Optimization log file can be found here

Table 16: Results summary for optimization of ethene

Optimized structure	Results Summary	Point Group	Energy/Hartrees HF/3-21G
Optimized structure of ethene		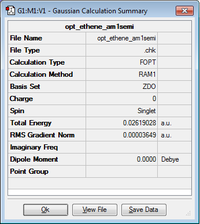D2h	0.026190

Molecular orbitals for cis butadiene

HOMO for ethene	LUMO for ethene

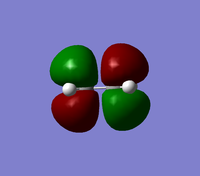
From the orbital description above it can be seen that the HOMO is symmetric with respect to the plane, whilst the LUMO is antisymmetric.

Optimizing to transition state for ethene + cis butadiene

In this section the method that will be used to optimize to a transition state will be the TS Berny method used earlier, however in this case the method used will be the one specified earlier. In the previous sections both ethene and cis butadiene were optimized. Using these optimized structures, a guess transition structure will be inputted into GaussView. The guess structure was given an interfragment distance of 2.26Å. This distance was used as it was found from a report containing information about the transition structure. Optimization log file can be found here

Table 17: Results for optimization of ethene + cis butadiene to a transition structure

Optimized structure	Results Summary	Energy/Hartrees HF/3-21G
Optimized ethene + cis butadiene transition structure		0.111655

The above results show the energy of the transition structure and once again in order to prove this is the transition structure there should be a presence of an imaginary frequency. From checking the log file an imaginary frequency is found at -955.91cm^-1.

Animation of imaginary frequency for ethene + cis butadiene

The animation shows a reasonable imaginary frequency as it is clear that the terminal carbons which will react are moving towards and away from each other and the C--C bond is forming C=C. From this it can be concluded that the formation of the two bonds is synchronous as both fragments move towards and away from each other at the same time. In contrast to this is the animation shown below for the lowest positive frequency at 146.99cm^-1.

Animation of lowest positive frequency for ethene + cis butadiene

The lowest positive frequency does not seem to resemble the forming bonds like the imaginary frequency does, as the fragments are not moving towards or away from each other. This can be explained by understanding that the negative frequency is the only frequency which shows the bond forming. This is because at the top of the 'hill' on the reaction co-ordinate, the reaction can go forwards and form a bond, or move backwards to break the bond, therefore that vibration shows bonds forming and breaking. However, all of the positive frequencies which follow are orthogonal to the imaginary frequency and therefore none of them represent formation of bonds. Although, in some cases there may be slight asynchronous bond forming.

Optimization log file for IRC can be found here

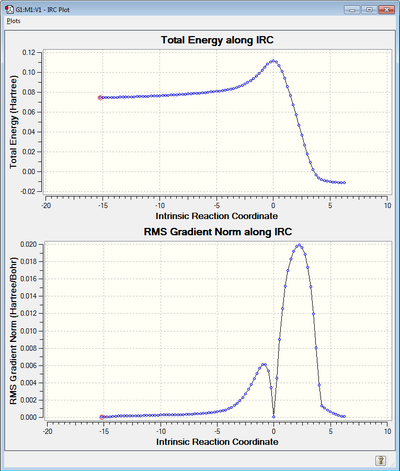
Reaction co-ordinate	IRC for 100 points (both directions)

An IRC calculation was also run in both directions at steps = 100 and force constants calculated always. From the total energy IRC graph the reaction co-ordinate can be seen to go through a maximum energy state which is the transition state and then follow a trajectory until a minimum is reached, this minimum is the product. The graph showing the gradient shows how the trajectory followed is the path of steepest descent due to a steep curve being seen. Additionally at the maximum and minimum the gradient tends to 0.

Molecular orbitals for transition structure of ethene + cis butadiene

HOMO for transition state	LUMO for transition state

AS = Antisymmetric, S = Symmetric, Symmetry described is always with respect to the nodal plane

The molecular orbitals of the transition state show that the HOMO is antisymmetric and the LUMO is symmetric with respect to the plane. Additionally, observing the HOMO and LUMO for the reactants, it can also be seen that the HOMO of cis butadiene (AS) combines with the LUMO of ethene (AS) to form the antisymmetric HOMO for the transition state. Furthermore, to form the symmetric LUMO of the transition state it is the combination of the LUMO of cis butadiene (S) and HOMO of ethene (S).

Analyzing the geometry of the Diels Alder Reaction

Below is the table showing the bond lengths of the corresponding C-C bonds which are labelled in the image on the right.

Table 18: Bond lengths for ethene + cis butadiene transition state

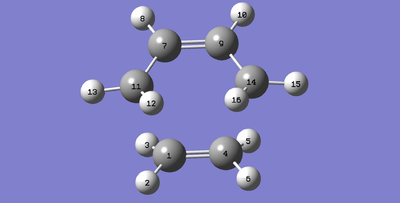
Atoms	Bond Length (Å)
C1-C11	2.11937
C1-C4	1.38290
C4-C14	2.11896
C9-C14	1.38184
C7-C9	1.39755
C7-C11	1.38164

Before discussing the results it is necessary to know that the average bond length for an sp³ C-C bond is 1.54Å and for an sp² C=C bond it is 1.46Å. From the reaction between ethene and cis butadiene we know that a single C-C bond will form between C1-C11 and for that reason it can be seen to have reduced from the set bond length given in the input file (2.26Å). The same can be said for C4-C14. This means there is some attraction between these terminal carbons on each fragment of the product. If there was a repulsive force present then the sum of the van der Waals radii for each carbon atom would be greater than or equal to 3.40Å.

(Perhaps more important is to say that the lengths r_C1-C11 and r_C4-C14 being below 2*r_VdW indicate that bonds are being formed here. In addition - looking at the other bond lengths around the cyclic TS - you can see the bonds are somewhere in between a single and a double (I don't agree with your statement that a C=C bond length is 1.46Å, I'd say somewhere around 1.33-1.35Å). This makes sense as the π bonds are breaking and a new π bond is forming at C7-C9 Tam10 (talk) 12:22, 28 October 2015 (UTC))

The regioselectivity of the Diels Alder reaction

The reaction that will now be discussed will be of maleic anhydride (electron poor dienophile) and cyclohexa-1,3-diene (electron rich diene). A drawing made on ChemDraw was shown in the introduction of the Diels Alder Cycloaddition. The outcome of this particular reaction forms two products, the exo and the endo product. In this computation we will find out which product is preferred, and therefore know what the preferred transition structure is.

Optimization of cyclohexa-1,3-diene

Optimization log file can be found here

Table 19: Optimization of cyclohexa-1,3-diene

Optimized structure	Results Summary	Point Group	Energy/Hartrees HF/3-21G
Optimized structure of cyclohexa-1,3-diene		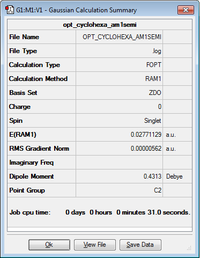C2	0.027711

The above table shows the results summary for the optimization of cyclohexa-1,3-diene.

Molecular orbitals for cyclohexa-1,3-diene

HOMO for cyclohexa-1,3-diene	LUMO for cyclohexa-1,3-diene

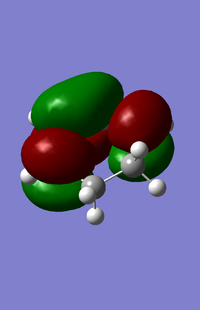
From the above orbitals the HOMO is antisymmetric and LUMO symmetric with respect to the plane.

Optimization of Maleic Anyhydride

Optimization log file can be found here

Table 20: Optimization of maleic anhydride

Optimized structure	Results Summary	Point Group	Energy/Hartrees HF/3-21G
Optimized structure of maleic anhydride		Cs	-0.12182

Molecular orbitals for maleic anhydride

HOMO for maleic anhydride	LUMO for maleic anhydride

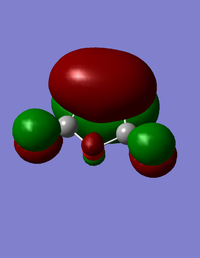
The HOMO for maleic anhydride is symmetric, and the LUMO is antisymmetric with respect to the plane.

Optimization of Exo product

Optimization log file can be found here

Table 21: Optimization of exo product

Optimized structure	Results Summary	Point Group	Energy/Hartrees HF/3-21G
Optimized structure of exo product		C1	-0.21387279

Optimization of Endo product

Optimization log file can be found here

Table 22: Optimization of endo product

Optimized structure	Results Summary	Point Group	Energy/Hartrees HF/3-21G
Optimized structure of endo product		C1	-0.21387259

Optimizing to transition state for Cyclohexa-1,3-diene + Maleic Anhydride

Following the same procedure as we have been, the previously optimized reactants (cyclohexa-1,3-diene and maleic anhydride) will be used to form an exo and endo transition state.

Optimizing to the exo transition state

From studying the tutorial exercise out of the three methods tried, the best one seemed to be QST2. This is because it is fully automated and the input file must only contain a reasonable guess transition structure. For that reason the product also needed to be optimized.

In this method the reactants and products need to be in the same window as shown earlier when optimizing the boat transition strucutre, in addition to this the labels of the atoms need to be the matching so the interpolation can occur.

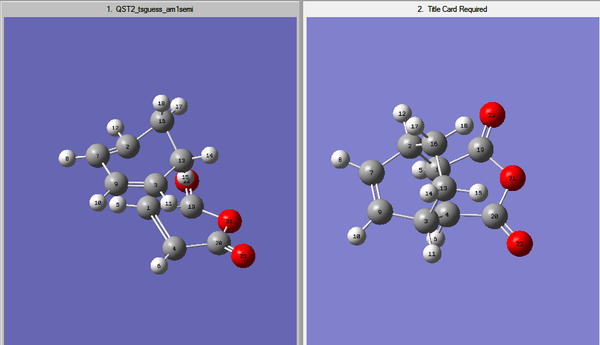
The above image shows the matching labelling.

Optimization log file can be found here

Table 23: Optimization of exo transition state

Optimized structure	Results Summary	Point Group	Energy/Hartrees HF/3-21G
Optimized exo transition state		C1	-0.05041879

A negative frequency was found at -812.20 cm^-1, confirming it is a transition structure.

Animation of imaginary frequency for exo transition state

Molecular orbitals for exo transition state

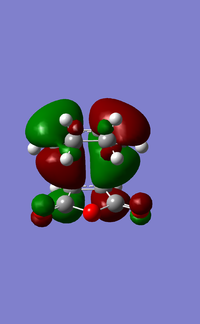
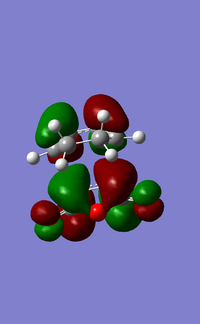
HOMO for exo transition state	LUMO for exo transition state

From the orbitals you can see that the HOMO is antisymmetric and the LUMO is also antisymmetric with respect to the plane.

Optimizing to the Endo transition state

The same method was used for this structure.

Optimization log file can be found here

Table 24: Optimization of endo transition state

Optimized structure	Results Summary	Point Group	Energy/Hartrees HF/3-21G
Optimized endo transition state		C1	-0.21387259

A negative frequency was found at -812.20 cm^-1, confirming it is a transition structure.

Animation of imaginary frequency for endo transition state

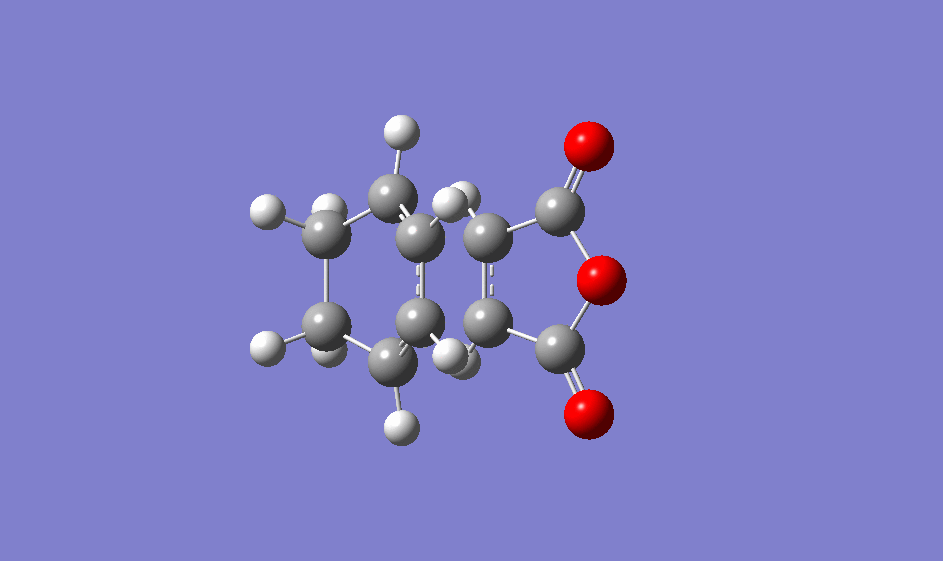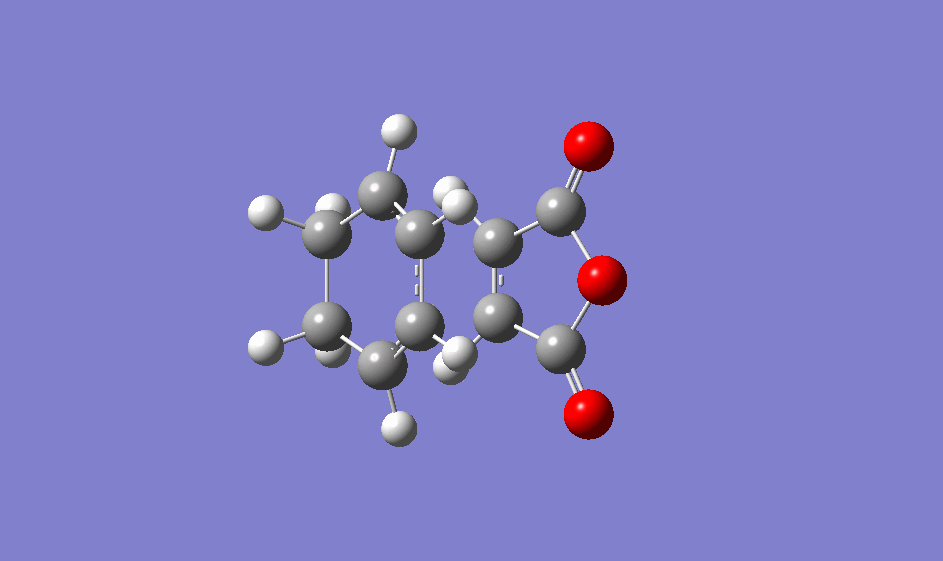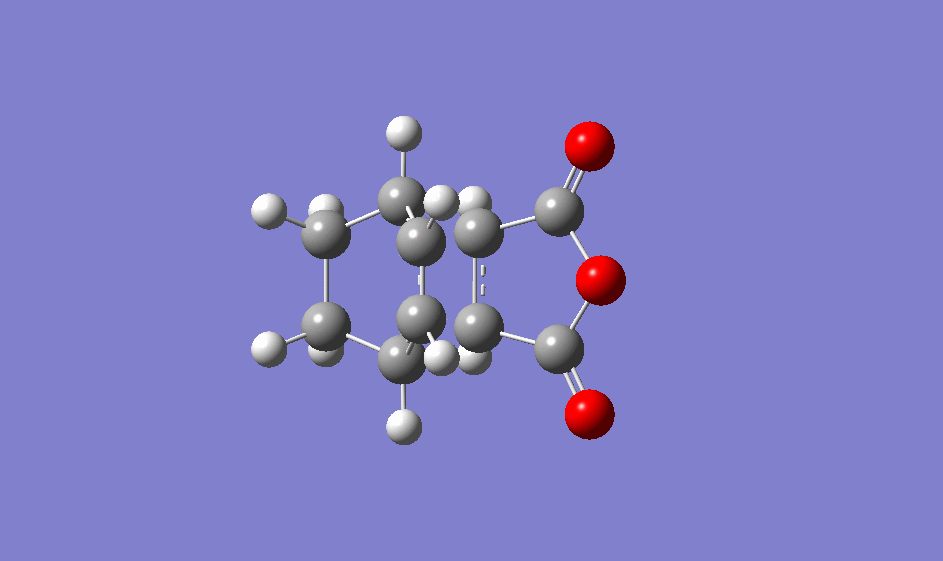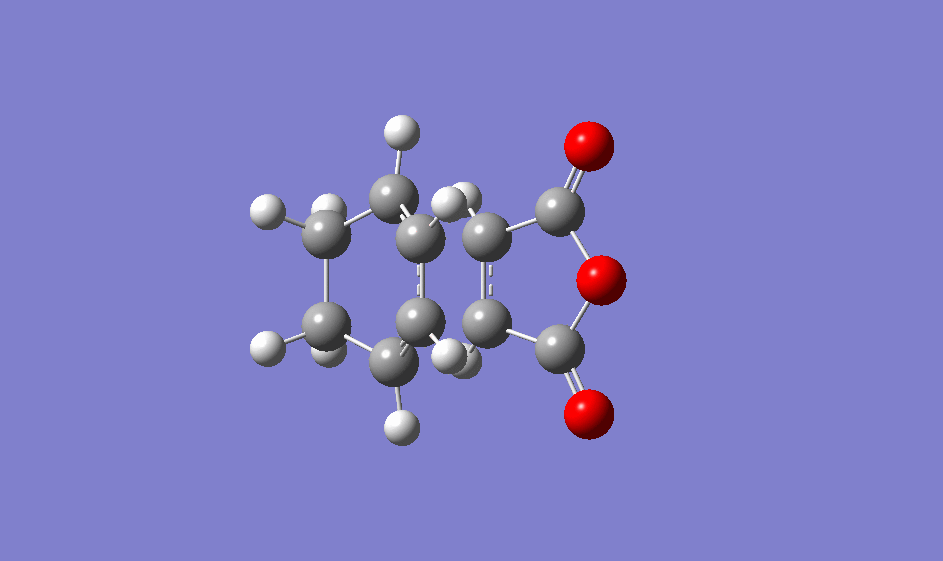
The imaginary frequency was observed at -806.48cm^-1

Molecular orbitals for endo transition state

HOMO for endo transition state	LUMO for endo transition state

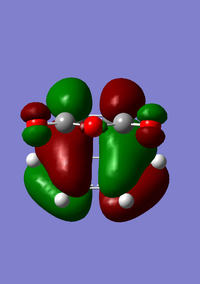
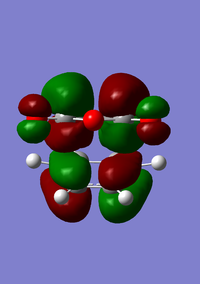
For the endo product there is similarity to the exo product in which both molecular orbitals are antisymmetric with respect to the plane.

Comparing the exo and endo transition structures

Table 25: Summary of energies for exo, endo and reactants at AM1 (Semi-Empirical) and B3LYP/631G(d) (Hartree)

	AM1 Semi-Empirical			B3LYP/6-31G(d)
	Electronic energy	Sum of electronic and zero-point energies	Sum of electronic and thermal energies	Electronic energy	Sum of electronic and zero-point energies	Sum of electronic and thermal energies
		at 0 K	at 298.15 K		at 0 K	at 298.15 K
Exo TS	-0.05041879	0.134880	0.144881	-612.679335	-612.498004	-612.487667
Endo TS	-0.05150476	0.133494	0.143683	-612.683396	-612.502207	-612.491836
Reactant (cyclohexa-1,3-diene)	0.02771129	0.152502	0.157726	-233.418911	-233.296118	-233.290938
Reactant (maleic anhydride)	-0.12182418	-0.063346	-0.058192	-379.289534	-379.233649	-379.228464

The above table shows the energies of the reactants and the transition states. From this we can find the activation energies and therefore know which is the preferred transition structure. With this information relative energies can be calculated between the exo and endo transition states. If the endo transition state is set to have 0 kcal mol^-1, then the exo transition state has a value of 0.6815 kcal mol^-1 when using the AM1 method. Relative energy for the DFT method gives the exo transition state 2.5479 kcal mol^-1, higher than the endo form. Both relative energies were calculated using the electronic energy. Hence, the endo transition structure is lower in energy and therefore the preferred transition path.

Table 26: Summary of activation energies (in kcal mol^-1)

	AM1 Semi-Empirical	AM1 Semi-Empirical	B3LYP/6-31G*	B3LYP/6-31G*	Expt.
	at 0 K	at 298.15 K	at 0 K	at 298.15 K	at 0 K
ΔE (Exo TS)	28.69	27.42	19.93	18.27	-
ΔE (Endo TS)	27.82	26.74	17.29	15.72	-

The activation energies also confirm the endo state being the preferred state due to its lower activation energies. In both methods used the endo state has a lower activation energy. In the AM1 method the difference between the activation is not very large however the difference is profound when using the 631G(d) method, where a clear difference can be seen.

Table 27: Bond lengths for exo transition state

Atoms	Bond Length (Å)
C1-C2	2.16809
C3-C4	2.17268
C1-C4	1.41010
C3-C9	1.39424
C7-C9	1.39674
C2-C7	1.39448
C13-C20	2.94523

Table 28: Bond lengths for endo transition state

Atoms	Bond Length (Å)
C1-C2	1.39307
C3-C4	1.39304
C1-C4	1.39726
C3-C9	2.16250
C7-C9	1.40846
C2-C7	2.16250
C4-C20	2.98356

From the above tables a geometric analysis can be done. From the bond lengths the exo and endo forms both have different lengths. For the C-C single bonds which are forming the endo structure has a shorter bond length. This has occurred due to the orbital overlap in the endo structure being more favourable leading to a better interaction. Similarly to an earlier geometric analysis to do with bond lengths, the van der Waals radii for the C-C bond is less than 3.4Å, therefore showing a favourable interaction and not a repulsive one. The distance between the -(C=O)-O-(C=O)- fragment of the maleic anhydride and the C atoms of the opposite -CH₂CH₂- for the exo transition structure is found to be 2.94523Å. For the endo the opposite -CH=CH- is used and a distance of 2.98356Å is seen. Once again it is below 3.4Å and therefore means there is some attractive interaction between these carbon atoms. Furthermore, the strain in the system can also be explained. It seems as though the endo form is less strained due to it having a shorter bond distance at the terminal carbon atoms where the new sigma bond will be formed, this will then have an effect on the maleic anhydride, as in the endo state the maleic anhydride is closer to the cyclohexa-1,3-diene and therefore will be less strained. Whereas in the exo transition state the maleic anhydride is more strained due to it being further away. Moreover, this means that the secondary orbital overlap effect is great enough to allow the endo transition state to predominate.

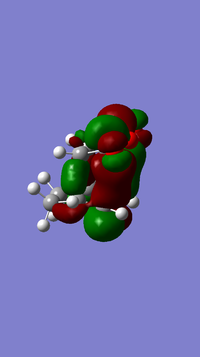
Secondary Orbital Overlap Effect

Using basic frontier molecular orbital theory the exo product should be the most thermodynamically stable and therefore be the preferred product. However the endo product is found to be the most stabilized, this is to do with its additional orbital interactions. Both the endo and the exo have favourable primary orbital overlap effects however the endo has secondary orbital effects. These are when the dienophiles π system and the dienes π system have a favourable interaction. The interaction which occurs is a non-bonding one, this is why it does not contribute to any bonding which occurs in the molecule, however due to its presence it lowers the activation energy and therefore provides the fastest path for the mechanism to go through. Therefore, the most kinetically stable product is the endo product.

Molecular orbitals for endo transition state showing Secondary Orbital Overlap Effect

LUMO+2 for endo transition state	LUMO+2 for exo transition state

The above molecular orbital shows the secondary orbital overlap present in the endo transition structure, this overlap is not possible in the exo transition structure as shown in the figure above, and therefore is higher in energy. The non-bonding interaction which is present is between the C=O lobes and the back lobes of the HOMO of the electron rich diene. In the exo product the approach of the diene means the orbitals from the C=O which are needed for the secondary orbital overlap are pointing away from the diene and therefore no secondary orbital interaction is possible. This leads to the endo product being the major product, whilst the exo product is minor. The transition energy is lowered, hence the rate is faster. However, in some experimental reactions the exo form can prevail, but this is dependant upon the reaction conditions set.

Conclusion

To conclude in this computation the mechanism of the Cope Rearrangement and the Diels Alder reaction were examined using GaussView + Gaussian. The computations confirmed many of the theories mentioned in the background information. For instance the fact that the reaction is a concerted pericyclic reaction was confirmed when looking at the transition structure and seeing the presence of a synchronous vibrational frequency. In addition three methods were used, and for the Diels Alder computation the method used was the QST2 method. This method worked well, however a good guess of the transition structure is necessary, as when the computation was run without a given distance the computation failed. Overall, the preferred mechanism is to go through the endo transition structure as through activation energy calculations, the exo transition structure gave a higher activation energy.

Throughout the Diels Alder section, Austin Model 1 (AM1) Semi-empirical method was used, this was because it is a fast method which also gives accurate data. When comparing data found from this computation to other literature the values were in good agreement. However, I think that this method would not be ideal for a more complicated reaction, if the reactants contained more bulky groups which would lead to different stereochemistry this method may fail and a higher level of theory may be necessary. In addition to that as mentioned earlier, an inorganic reaction would require or more accurate method such as PM3 or PM5.

In a future computation it would be good to try the other two methods discussed in the first section (Frozen co-ordinates and TS Berny) for the Diels Alder reaction. These were tried however the reaction failed due to computation errors and therefore information outputted by Gaussian was not accurate nor reliable. The reason the other two methods may be more useful is because the QST2 method requires good knowledge of the transition structure. This is a downside as for some reactions data may not be known and then a QST2 can not be run, leaving TS Berny to be the method of choice. Finally, the QST3 method would be good to try, especially because it does not need good knowledge of the transition state, only the reactants, products and a guess transition state.