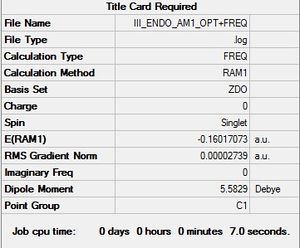
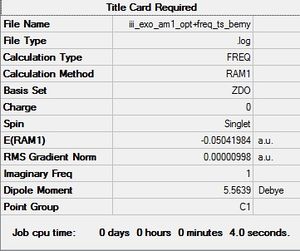
Rep:Mod:kl1111ts

Transition States: Computational Chemistry

Introduction

In this study, GaussView (Technically, you are using another program called Gaussian, to perform the calculations. You are using GaussView to interact with and prepare input for Gaussian. João (talk) 18:57, 1 April 2015 (BST)) was used to locate the transition states for different reactions. One of the reactions involved the Cope rearrangement and the transition structure was obtained by depicting the gauche and anti conformers of 1,5-hexadiene and optimizing to the Hartree Fock level or DFT level. This calculation lead to the chair and boat transition states being obtained (Does structural information of the stable conformers directly give you information about the transition state? João (talk) 18:57, 1 April 2015 (BST)). The transition state was confirmed by frequency analysis to find an imaginary frequency corresponding to a maximum on the potential energy surface (If one imaginary frequency were indicative of a maximum of the potential energy surface, what would two imaginary frequencies indicate? João (talk) 18:57, 1 April 2015 (BST)).

The transition states were optimized using a variety of methods, including (i) Hessian Method (ii) Frozen Coordinate Method (iii) QST2 (iv) QST3 and the results of these calculations lead were compared to pre-determined values to see which gave more reliable results.

The Diels-Alder reaction between maleic anhydride and cyclohexa-1,3-diene was also calculated to obtain the endo and exo transition structures. The endo transition state has been found to be lower in energy compared to the exo state and reasons for this will be explained for in this study.

Cope Rearrangement: Optimizing the Reactants and Products

Cope Rearrangement of 1,5-hexadiene

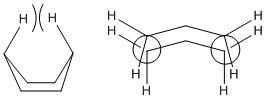
The Cope Rearrangement is a concerted pericyclic reaction that involves a [3,3]-sigmatropic shift rearrangement. The reaction involves the movement of 6 electrons and is known to proceed via either a chair or boat transition state. Previous work on the Cope Rearrangement has been done by Houk et al using the B3LYP/6-31G* level of theory and these results were compared to those calculated in this study.

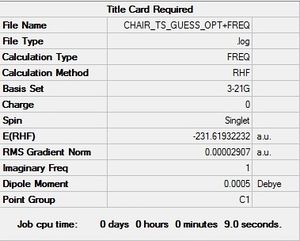
(a) HF/3-21G Optimization of anti 1,5-hexadiene

A molecule of 1,5-hexadiene was drawn with an anti-configuration. The structure was then cleaned and optimized using the Hartree-Fock method and 3-21G basis set. Details of the optimized molecule can be found below.

summary data	convergence	Jmol
	.log file Item Value Threshold Converged? Maximum Force 0.000029 0.000450 YES RMS Force 0.000007 0.000300 YES Maximum Displacement 0.000972 0.001800 YES RMS Displacement 0.000374 0.001200 YES Predicted change in Energy=-1.056856D-08 Optimization completed. -- Stationary point found.	optimised 1,5-hexadiene molecule(anti1)

The energy was found to be -231.69260a.u, corresponding to the anti1 conformer found in appendix 1. The symmetry of the molecule was then locked to the C₂ point group.

(b) HF/3-21G Optimization of gauche 1,5-hexadiene

There are many conformers of 1,5-hexadiene and this time, the gauche conformer was drawn in Gaussview. The anti conformer is expected to be more stable compared to the gauche form due to the addition of σ C-H / σ* C-H orbtial interactions that are possible in this conformation.

Using the same method in part (a), the gauche conformer was cleaned and optimized at the Hf/3-21G level of theory and the details can be found below.

summary data	convergence	Jmol
	.log file Item Value Threshold Converged? Maximum Force 0.000137 0.000450 YES RMS Force 0.000027 0.000300 YES Maximum Displacement 0.001470 0.001800 YES RMS Displacement 0.000554 0.001200 YES Predicted change in Energy=-9.727792D-08 Optimization completed. -- Stationary point found.	optimised 1,5-hexadiene(gauche1) molecule

The energy of this molecule was found to be -231.68772a.u, corresponding to the gauche2 conformer as found in apprendix 1. As predicted, the energy of this conformer is slightly higher than that of the anti-conformer found in part (a), by a marginal 0.00489a.u. The symmetry of the molecule was found to be of the C₂ point group, same as that found for part (a).

(d) The many confromers of 1,5-hexadiene

In total, there are 10 conformers of 1,5-hexadiene, all of varying energies. The ten structures were all optimised at the HF/3-21G level of theory to allow for comparison.

Comparison of the ten 1,5-hexadiene structures

Conformer (gauche)	Jmol image	Point Group	Energy (au)	Conformer (anti)	Jmol image	Point Group	Energy (au)
gauche1.log		C2	-231.68771605	anti1.log		C2	-231.69260236
gauche2.log		C2	-231.69166698	anti2.log		Ci	-231.69253519
gauche3.log		C1	-231.69266121	anti3.log		C2h	-231.68907055
gauche4.log		C2	-231.69153032	anti4.log		C1	-231.69097057
gauche5.log		C1	-231.68916015
gauche6.log		C1	-231.68916019

From the table above, it can be seen that five of the ten conformers have energies which are higher than the rest. analysis of their structures show that the vinyl protons are in close proximity of each other and this leads to unfavourable steric interactions (I'm unsure what structures you are including in this analysis. I suppose that ant3 has a relativelly high energy, are the vinyl protons in close proximity in this case? João (talk) 18:57, 1 April 2015 (BST)). The lowest energy conformation is gauche3 in which these steric interactions are minimized.

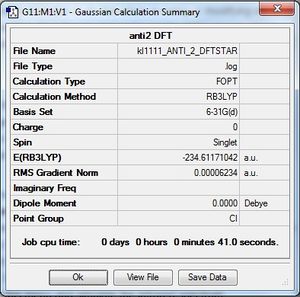
(e) The C_i anti2 conformer of 1,5-hexadiene

The anti 2 conformer of 1,5-hexadiene was found and optimized at the HF/3-21G level of theory and the .log file and details of its energy and C_i point group can be found in the table above in part (d). The final energy of the molecule was found to be -231.69253519au, and this is in very good agreement with the energy value of -231.69254au found in appendix 1 and proves that the molecule optimized is the anti2 conformer.

(f) B3LYP/6-31G Optimization of anti2 1,5-hexadiene

In part (d), the anti2 conformer of 1,5-hexadiene was found and optimised at the HF/3-21G level of theory. Although this provided us with the correct conformation, the basis set used was of a low level and a better approximation can be found using a higher basis set and this was done at the B3LYP/6-31G level. (In this calculation you are not only using a larger basis set but you are also using a different method to calculate the electronic energy, DFT with the B3LYP functional, which accounts for electronic correlation. João (talk) 18:57, 1 April 2015 (BST))

summary data	convergence	Jmol
	.log file Item Value Threshold Converged? Maximum Force 0.000145 0.000450 YES RMS Force 0.000030 0.000300 YES Maximum Displacement 0.000909 0.001800 YES RMS Displacement 0.000398 0.001200 YES Predicted change in Energy=-2.061304D-07 Optimization completed. -- Stationary point found.	reoptimised 1,5-hexadiene(anti2) molecule

The reoptimised structure at DFT level was compared to that of the HF level. Despite the structure appearing to be identical, there were geometrical differences found in terms of bond lengths and angles.

Depiction of the geomtrical differences in anti2 due to different basis sets

		Dihedral Angles (°)			Bond Lengths (Å)
	Basis Set	C1-C2-C3-C4	C2-C3-C4-C5	C3-C4-C5-C6	C1-C2	C2-C3	C3-C4
	HF/3-21G	114.67491	180.00000	-114.67491	1.31614	1.50891	1.55299
	B3LYP/6-31G*	118.58058	180.00000	-118.58058	1.33344	1.50418	1.54863

Analysis of the two structures show that the bond lengths remain almost identical. An interesting observation to make however is the difference in dihedral angles by 3.90567°. Despite the small change in the angle, there is a significant difference in energy of 1833.98 kcalmol^-1 (One cannot directly compare the absolute values of energy calculated with different methods, as different references are used in different methods. João (talk) 18:57, 1 April 2015 (BST)). Since this energy difference is quite significant, it can be concluded that a higher basis set is used in order to obtain reliable energies in further investigations.

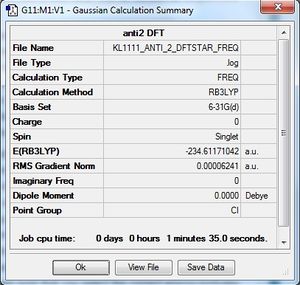
(g) Frequency Analysis of 1,5-hexadiene

A frequency analysis was carried out on the DFT optimised structure of anti2 1,5-hexadiene. This procedure was done to ensure that a minimum had been found as opposed to a maximum. If the frequencies obtained are real and positive, then a minimum has been found. In the case of a maximum, there would be an imaginary frequency present, corresponding to a transition state. (What is the difference between a maximum and a saddle point? Is the transition state a maximum or a saddle point? João (talk) 18:57, 1 April 2015 (BST))

Summary	Frequencies
	.log file Low frequencies --- -11.4908 -3.3437 -1.5715 0.0007 0.0009 0.0010 Low frequencies --- 73.1085 80.3350 120.8830

As seen above, the structure showed no imaginary frequencies and thus confirms that it is a minimum state.

	0K	298K
Σ Electronic and Zero Point Energies (au)	-234.469218	-234.469218
Σ Electronic and Thermal Energies (au)	-234.469218	-234.461866
Σ Electronic and Thermal Enthalpies (au)	-234.469218	-234.460922
Σ Electronic and Thermal Free Energies (au)	-234.469218	-234.500814

The thermochemistry data from two temperatures (0K and 298K) were compared and these can be seen in the table above. Σ Electronic and Zero Point Energies corresponds to the potential energy of the molecule at 0K and this includes the zero point vibrational energy (E = Eelec + ZPE). Σ Electronic and Thermal Energies refers to the energy of the molecule at 298.15K and 1 atm pressure and this includes contributions from translational, vibrational and rotational energy modes (E = E + Evib + Erot + Etrans). By using a correctional term to account for RT, Gaussview can also predict the enthalpy (H = E + RT) and the Gibbs free energy (G = H - TS) at a chosen temperature.

When comparing the energies at the twp temperatures, it can be seen that there is no difference in the zero point energies and this is to be expected since this will always be calculated at 0K. Another interesting observation is that all the energies at 0K are the same since there will be no contribution from vibrational, translational or rotational modes.

Optimizing the "Chair" and "Boat" Transition Structures

The chair and boat transition structures for the Cope rearrangement can be identified as being made up of two C₃H₅ allyl fragments, one of C_2v symmetry and the other of C_2v symmetry. For this reason, a C₃H₅ allyl fragment was drawn and optimised and then two of the fragments put together at a distance of 2.2Å apart. This structure represents the transition structure for the Cope rearrangement that will follow (It does not correspond to a transition structure yet, but rather an initial guess for it. João (talk) 18:57, 1 April 2015 (BST)). The transition states were then optimised using a variety of methods and these include (i) computing the fporce constants at the beginning of every calculation, (ii) using the redundant coordinate editor and frozen coordinate and (iii) using the Quadratic Synchronous Transit Method (QST2 and QST3).

(a) HF/3-21G optimization of an allyl fragment

A C₃H₅ allyl fragment was drawn in Gaussview and optimized at the HF/3-21G level. As seen in the table below, the fragment was found to have C_2v symmetry.

summary data	convergence
	.log file Item Value Threshold Converged? Maximum Force 0.000045 0.000450 YES RMS Force 0.000017 0.000300 YES Maximum Displacement 0.000188 0.001800 YES RMS Displacement 0.000080 0.001200 YES Predicted change in Energy=-1.117357D-08 Optimization completed. -- Stationary point found.

(b) Berny Optimization of the Chair Transition State

Following creation of the allyl fragment, this was pasted into a new window, appended and arranged into a structure that resembled the chair transition structure. An optimization to the berny transition state was carried out simultaneously to a frequency analysis. The force constant was calculated once and the additional keywords "Opt=NoEigen" was input to prevent the calculation from crashing if more than one imaginary frequency was detected. This may occur if the estimated transition structure is not good enough.

After the calculation had been run, the distances between the terminal carbons were found to be 2.02Å. As stated previously, a transition structure can be confirmed to be found if there is an imaginary frequency detected. Analysis of the vibrations in the structure showed the presence of an imaginary frequency at -817.87 cm^-1, providing evidence for the detection of the transition state.

Summary Data	Convergence and Frequency Data	Vibration Animation
/ .log file	Item Value Threshold Converged? Maximum Force 0.000088 0.000450 YES RMS Force 0.000014 0.000300 YES Maximum Displacement 0.001593 0.001800 YES RMS Displacement 0.000374 0.001200 YES Predicted change in Energy=-1.597977D-07 Optimization completed. -- Stationary point found. Low frequencies --- -817.8668 -4.5693 -0.0008 -0.0008 -0.0008 4.5750 Low frequencies --- 5.6228 209.4628 395.5866 ****** 1 imaginary frequencies (negative Signs) ******

(c+d) Frozen Coordinate Method of Optimizing the Chair Transition Structure

This method locates the transition structure by freezing the reaction coordinate and then minimizing the rest of the molecule. The reaction coordinate is then unfrozen and the optimization restarted. The advantage of using this method is that it can give a better transition structure (What would make it a better transition structure? Do you expect a different structure at all? João (talk) 18:57, 1 April 2015 (BST)) and may save time as the whole Hessian may not need to be calculated.

During this calculation, the terminal carbons in which the bonds are formed and broken were frozen by changing "Unidentified -> Bond" and "Add -> Freeze Coordinate" in the Redundant Coordinate Editor. The structure was then optimized to a minimum at the Hartree Fock level and the additional keywords "Opt=ModRedundant" were present in the method.

Summary Data	Convergence Data
	.log file Item Value Threshold Converged? Maximum Force 0.000109 0.000450 YES RMS Force 0.000019 0.000300 YES Maximum Displacement 0.001443 0.001800 YES RMS Displacement 0.000442 0.001200 YES Predicted change in Energy=-1.596429D-07 Optimization completed. -- Stationary point found.

The result from the first optimization can be found in the table above.

Following this initial optimization, the frozen bonds were unfrozen by changing "Freeze Coordinate -> Derivative" in the Redundant Coordinate Editor and an optimization carried to a transition state and no force constants were calculated. This resulted in the table below

Summary Data	Convergence Data
	.log file Item Value Threshold Converged? Maximum Force 0.000072 0.000450 YES RMS Force 0.000014 0.000300 YES Maximum Displacement 0.000625 0.001800 YES RMS Displacement 0.000166 0.001200 YES Predicted change in Energy=-5.334947D-08 Optimization completed. -- Stationary point found.

The structures obtained from parts c and d look identical. However, there are minor differences in the bond lengths due to the different methods used to optimize the transition state.

	Hessian Method	Frozen Coordinate Method
Bond Forming/ Breaking Distance (Å)	2.02090	2.02011
	2.02119	2.01982

As seen in the table above, the calculated bond lengths differ only by 0.00108Å. Computed bond lengths are generally only accurate to 0.01Å so it can be said that the two methods used gave identical results.

(e) QST2 Method of Optimizing the Boat Transition State

In this method, both the reactants and products are drawn into Gaussview. Both structures are plotted on a potential energy surface and a line is linearly interpolated between the two in order to make an approximate reaction pathway. The transition structure obtained using this method is the maximum predicted in the potential energy surface.

In order to create the transition structure, the reactants and products must be numbered in such a way that shows where the bonds have broken and reformed. The anti2 molecule of 1,5-hexadiene was used for this purpose, arranged and renumbered in the following way:

Reactants	Products

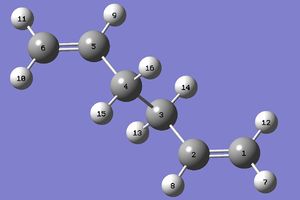
After renumbering the two structures, an opt+freq calculation was run and the optimization done to TS (QST2). The calculation was found to fail and the structure obtained appeared to show bonds forming between the wrong terminal carbons. One of the allyl fragments were translated directly over the other and a rotation of one of the molecules was not considered. For this reason, the calculation was not able to complete and the failed structure can be seen in the diagram below: (In which way is the calculation a failure? Are you sure the calculation did not finish with a converged result? In which way is the structure you obtained different from a chair transition state? João (talk) 18:57, 1 April 2015 (BST))

Failed QST2 Transition State

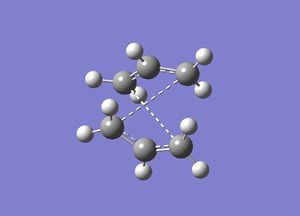
Since the QST2 method could not locate the transition state from the reactants and products above, the molecules were rearranged to form a structure that looked more similar to the boat transition structure to help the calculation run better. The molecules were bent to form a structure that somewhat resembled the gauche2 structure obtained previously (Wouldn't it be a eclipsed structure instead of gauche? João (talk) 18:57, 1 April 2015 (BST)) , and then renumbered as done before.

Reactants	Products

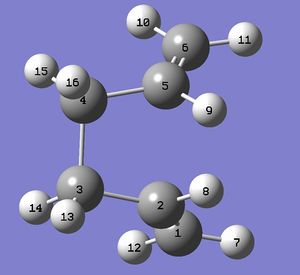
An opt+freq calculation was run once again to the QST2 transition state at the HF/3-21G level.

Summary Data	Convergence Data	Animation
	.log file Item Value Threshold Converged? Maximum Force 0.000082 0.000450 YES RMS Force 0.000028 0.000300 YES Maximum Displacement 0.001317 0.001800 YES RMS Displacement 0.000415 0.001200 YES Predicted change in Energy=-4.676287D-07 Optimization completed. -- Stationary point found. Low frequencies --- -839.9087 -4.6502 -0.0012 -0.0011 -0.0007 2.3117 Low frequencies --- 2.8643 155.1834 382.0221 ****** 1 imaginary frequencies (negative Signs) ******

As seen in the table above, an imaginary frequency was obtained at -840 cm^-1, implying that the transition state had been found. The motion of vibration can be seen in the above table.

QST3 Method of Optimizing the Transition State

The QST3 method is an improvement to the QST2 method, in that in addition to the reactants and product structures, the guess of the transition state is also input and this extra piece of information leads to more reliable results.

The calculation was repeated on the original 1,5-hexadiene reactant and product molecules with unchanged angles and a guess transition state was added.

Structures of the 3 molecules used in the QST3 calculation

Reactants	Products	Guess Transition State

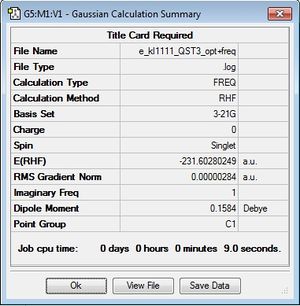
From this calculation, the following results were obtained:

Summary Data	Convergence Data	Vibration
	.log file Item Value Threshold Converged? Maximum Force 0.000007 0.000450 YES RMS Force 0.000002 0.000300 YES Maximum Displacement 0.000084 0.001800 YES RMS Displacement 0.000022 0.001200 YES Predicted change in Energy=-7.662039D-10 Optimization completed. -- Stationary point found. Low frequencies --- -839.9519 -1.0857 -0.9670 -0.0006 0.0005 0.0007 Low frequencies --- 0.8164 155.2795 381.9846 ****** 1 imaginary frequencies (negative Signs) ******

The results obtained from the QST3 method are very similar to those obtained in the QST2 method. An imaginary frequency at -840cm^-1 was obtained, implying that a transition state had been found.

(f) Intrinsic Reaction Coordinate (IRC)

The intrinsic reaction coordinate is used to follow the minimum energy path from a transition structure down to its local minimum on a potential energy surface by taking small steps into the direction where the gradient of the energy surface is the steepest.

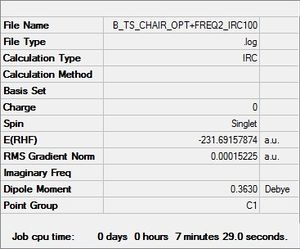
This calculation was done on the HF-3-21G optimized chair structure obtained in part b. Because the reaction coordinate is symmetrical, it was computed in the forward direction only. The force constants were set so that they were always calculated and the number of points along the IRC was modified to 50. The results obtained in this calculation can be seen in the table below.

Summary Data	Structure
.log file

As seen in the table above, the final structure of the molecule obtained after IRC looks very similar to the gauche 2 structure of 1,5-hexadiene. However, the energy is slightly higher than expected, and indicates that the minimum energy structure had not yet been located. For this reason, calculations were rerun in order to locate the minimum energy structure.

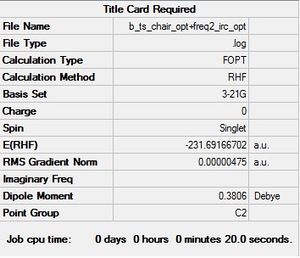
(i) Optimization to a minimum

In this method, a standard optimization to the minimum point was conducted. The results of this calculation can be seen below.

Summary Data	Convergence Data
	.log file Item Value Threshold Converged? Maximum Force 0.000010 0.000450 YES RMS Force 0.000003 0.000300 YES Maximum Displacement 0.000298 0.001800 YES RMS Displacement 0.000091 0.001200 YES Predicted change in Energy=-2.411499D-09 Optimization completed. -- Stationary point found.

After this optimization, the energy of the structure became closer to the value of the gauche2 value found in appendix 1, proving that a minimum energy structure had been located.

(ii) Increasing the number of points in IRC

In this step, the number of points in the IRC was increased from the initial 50 to 100. The results showed no difference from the 50 steps done previously because the calculation converged at 44 steps. For this reason, the structure obtained was very similar to that obtained previously and the data for the calculation can be seen below:

Summary Data

.log file

Usually, increasing the number of steps increases the chance of getting a reliable result because smaller geometry changes through the reaction coordinate can be monitored (These are two different things, the step size acts as you suggest, whereas the number of steps simply allows for more steps to be calculated in a case where the algorithm run out of steps without converging to the minimum. This is not what happened in your case, so increasing the number of steps has no effect. João (talk) 18:57, 1 April 2015 (BST)). Despite this advantage, it is time consuming and if the number of steps is increased to a very large number, the reaction coordinate may go down the wrong path and the final structure obtained may not be as expected. (How could increasing the number of steps (or decreasing their size) lead to the wrong result? João (talk) 18:57, 1 April 2015 (BST))

(g) Activation Energies

The activation energy for the reaction was calculated for both the chair and boat structure and this was done by reoptimizing the transition structures to the B3LYP/6-31G* level and then conducting frequency calculations. The chair TS used was from the frozen coordinate method and the boat TS was from the QST3 optimization.

The geometries of the two transition structures at different levels differ only by a small amount in the bond length and angles, and these can be seen in the two tables below.

Chair Transition Structure

	Bond Lengths (Å)
		HF/3-21G	B3LYP/6-31G*
	C1-C2	1.39	1.41
	C3-C6	2.02	1.97
	Bond Angles (°)
		HF/3-21G	B3LYP/6-31G*
	C1-C2-C3	120.51	119.92

Boat Transition Structure

	Bond Lengths (Å)
		HF/3-21G	B3LYP/6-31G*
	C1-C2	1.38	1.39
	C3-C6	2.14	2.21
	Bond Angles (°)
		HF/3-21G	B3LYP/6-31G*
	C1-C2-C3	121.70	122.26

After the calculation had run to completion, the .log file was analysed and for convergence and the thermochemistry data. Despite having near identical structures, the energy levels calculated at the two levels gave very different energies and these are tabulated below (Once more, it is not meaningful to compare absolute values of energy calculated with different methods.). For this reason, it is suggested that molecules are first optimized at a lower level of theory first and then reoptimized at a higher level in order to get more reliable results. (This is indeed correct, since the optimized geometries don't differ much, as you observed, one can use the simplest method to find a first approximation to the optimized structures. The advantage of the refinement with the higher level methods is not that absolute values of the energy are more meaningful, but that relative energies, such as the activation energy, are more accurate, as you note below. João (talk) 18:57, 1 April 2015 (BST))

Summary of Energies (a.u.)
	HF/3-21G			B3LYP/6-31G*
	Electronic Energy	Sum of Electronic and Zero-Point Energy at 0K	Sum of Electronic and Thermal Energies at 298.15K	Electronic Energy	Sum of Electronic and Zero-Point Energy at 0K	Sum of Electronic and Thermal Energies at 298.15K
Chair TS	-231.691322	-231.466705	-231.461344	-234.556931	-234.414910	-234.408982
Boat TS	-231.602802	-231.466705	-231.461344	-234.543078	-234.402352	-234.396009
anti2	-231.692535	-231.539537	-231.532561	-231.692535	-234.469219	-234.461869
Summary of Activation Energies (kcalmol-1)
		Activation Energy at 0K	Activation Energy at 298.15K		Activation Energy at 0K	Activation Energy at 298.15K
ΔE (Chair) kcalmol-1		45.70	44.69		34.08	33.19
ΔE (Boat) kcalmol-1		55.60	54.31		41.96	41.33

In the diagram above, it can be seen that the boat structure is eclipsed. This conformation leads to a higher degree of torsional strain compared to if it was in the staggered form (chair). There are also two hydrogen atoms within close proximity of one another which form Van der Waals interactions and thus further destabilizing the molecule. For these reasons, it can be expected that the boat conformation is higher in energy compared to the chair conformation and this can be seen in the table above where the electronic energy for the boat is 0.0139 au higher than for the chair conformation. Since the electronic energy of the boat conformation is higher than the chair conformation, it should also be expected for the activation energy to be higher as well and this is indeed the case as observed in the table above.

Experimentally activation energies for both transition states have been determined at 0K and these values correspond to 33.5 ± 0.5 kcalmol^-1 for the chair conformation and 44.7 ± 2.0 kcalmol^-1 for the boat conformation. When comparing the activation energies at 0K for both levels of theory, it is quite obvious that the B3LYP/6-31G* values are much closer than the HF/3-21G values to the experimentally obtained activation energies. This is to be expected, since the DFT method is a higher basis set than the HF method and will therefore give more accurate results.

The Diels Alder Cycloaddition of cis-Butadiene and Ethylene

The Diels-Alder cycloaddition reaction is an example of a pericyclic rearrangement in which the π electrons of an electron rich species interact with the π of an electron deficient species to form two new σ bonds (_π4_s+_π2_s cycloaddition). In the current study, the reaction involves the interaction between the HOMO and LUMO orbitals of cis-butadiene and ethylene. The reaction may only occur when there is significant electron overlap density, and only if they are of the same symmetry (Do the electronic density and molecular orbitals have the same symmetry? Which one is relevant in this case? João (talk) 18:57, 1 April 2015 (BST)). The total number of electrons involved in the reaction is six which follows the 4n+2 rule and thus the thermal reaction should proceed suprafacially via the Huckel transition state.

The mechanism for the reaction has been under much debate and controversy but it is now thought that it reacts via a concerted reaction via either a chair or boat transition state (What are a chair and boat transition states for this reaction? João (talk) 18:57, 1 April 2015 (BST)) with the boat being higher in energy due to unfavourable steric interactions.

(i) Optimization of cis-butadiene

To begin, a cis-butadiene molecule was drawn into Gaussview and it was optimized to the AM1 level.

Summary Data	Convergence Data	Image
	.log file
	Item Value Threshold Converged? Maximum Force 0.000030 0.000450 YES RMS Force 0.000011 0.000300 YES Maximum Displacement 0.000442 0.001800 YES RMS Displacement 0.000164 0.001200 YES Predicted change in Energy=-8.983817D-09 Optimization completed. -- Stationary point found.

The HOMO and LUMO orbitals were then visualized using the .chk file and the following images were obtained:

HOMO	LUMO
Antisymmetric	Symmetric

If a σ_v plane of symmetry is inserted through the molecule, it can be seen that the HOMO orbitals are antisymmetric with respect to the plane and the LUMO orbitals are symmetric with respect to the plane.

(ii) Finding the Transition State

The transition state has an envelope type structure and this arrangement of reactants maximizes the interaction between the π orbitals of the ethylene and butadiene molecules.

The transition state was drawn firstly by drawing the bicyclo system (a) seen in the diagram below and then removing the lower half to get structure (b). The distance between the two molecules was set to 2.00Å and it was then optimized to AM1 level.

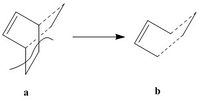
Summary Data

Convergence Data

.log file/.chk file Item Value Threshold Converged? Maximum Force 0.000050 0.000450 YES RMS Force 0.000007 0.000300 YES Maximum Displacement 0.000313 0.001800 YES RMS Displacement 0.000101 0.001200 YES Predicted change in Energy=-1.291588D-08 Optimization completed. -- Stationary point found. Low frequencies --- -956.2769 -2.4951 -0.0544 -0.0378 -0.0032 1.0929 Low frequencies --- 2.9091 147.2944 246.6162 ****** 1 imaginary frequencies (negative Signs) ******

As seen, an imaginary frequency was detected at -956cm^-1 and proves that a transition state was located. The vibration corresponding to the imaginary frequency is synchronous and does not break the symmetry of the molecule.

Imaginary Frequency	Lowest Positive Frequency

On the other hand, it can be seen that the lowest positive frequency vibration is asynchronous and breaks the symmetry of the molecule.

Because the imaginary frequency corresponds to a synchronous vibration, this Diels-Alder reaction must involve the concerted formation of two sigma bonds.

Geometry of the transition state

The image above shows the bond lengths between the carbon atoms. A typical C(sp²)=C(sp²) bond is usually between 1.31-1.34Å. In the reaction shown, there are three double bonds and these are located at C1-C2, C3-C4 AND C5-C6. However, the bonds obtained computationally are slightly longer than those in literature and it can therefore be assumed that there is some interaction between the two molecules that is causing the bonds to lengthen and become more similar to single bonds during the cycloaddition reaction.

In addition to this, it can be seen that the C2-C3 single bond is shorter than the value of 1.45-1.46Å that is expected for a conjugated C(sp³)-C(sp³) single bond. This may be attributed to the single bond becoming more similar to a double bond during the cycloaddition reaction.

The distance between C1-C6 is 2.12Å, this is shorter than the sum of Van der Waal's radii (3.40Å) and longer than that of a C(sp³)-C(sp³) bond of 1.53-1.55Å. This value suggests that a bond is beginning to form and since the distances between C1-C6 AND C4-C5 are identical, a concerted mechanism in which both bonds are formed at the same time is strongly implied.

Molecular Orbitals of the transition state

The molecular orbitals involved were then visualized and the bonding and antibonding interactions involving the HOMO of butadiene with the LUMO of ethylene, and the LUMO of butadiene with the HOMO of ethylene are shown below.

	HOMO	LUMO
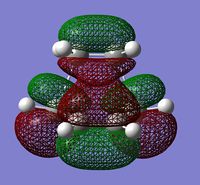
-0.32500au	-0.32393au	+0.02315au	+0.03377au
Symmetric	Antisymmetric	Symmetric	Antisymmetric

The energies of the molecular orbitals were obtained and can be seen above. In addition to this, a σ_v plane of symmetry was inserted through the molecule and the symmetry of the MO determined.

The HOMO was found to be symmetric with respect to the plane and is comprised of the antisymmetric HOMO of butadiene and the antisymmetric LUMO of ethylene. Since the symmetry of both MOs are the same, the reaction is allowed and a bonding interaction occurs to form 2 new σ bonds. (What about the LUMO? Does the reaction obey Woodward-Hoffmann rules? João (talk) 18:57, 1 April 2015 (BST))

(iii) Regioselectivity of the Diels-Alder Reaction

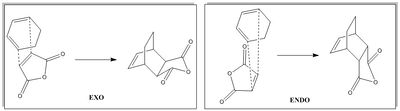
In the previous reaction between cis-butadiene and ethylene, the regioselectivity was not considered due to the ethylene molecule being completely symmetrical and thus only one product can be formed. In this section, the cycloaddition reaction between maleic anhydride and cyclohexa-1,3-diene will be considered. Maleic anhydride is not completely symmetrical and thus the reaction can give two products, the endo and exo form depending on the orientation of maleic anhydride relative to the cyclohexa-1,3-diene. The reaction is kinetically controlled (Doesn't this depend on the reaction conditions? João (talk) 18:57, 1 April 2015 (BST)) and it is the endo form which is preferred, despite the exo form being the more stable of the two. Reasons as to why the endo form is preferred over the exo form will be explored in this section.

The two reactants were drawn into GaussView and optimized under the AM1 level of theory.

Maleic Anhydride

Image	Summary

Cyclohexa-1,3-diene

Image	Summary

Locating the Transition Structures

In this section, the two products were drawn into GaussView and optimized to a minimum under AM1 level of theory. The transition state was then found using the frozen coordinate method where the reactants were separated by a distance of 2.00Å.

Endo transition state

Product	Transition State	Vibration
.log file	.log file/.chk file

The product was initially optimized a minimum before reoptimizing using the frozen coordinate method. As seen above, an imaginary frequency was located at -806.35 cm^-1 and proves that a transition state was found. The vibration is synchronous and implies that the two new sigma bonds are formed simultaneously in a concerted fashion.

Exo transition state

Product	Transition State	Vibration
.log file	.log file/.chk file

For the exo transition state, an imaginary frequency was located at -812.18 cm^-1 and proves that the transition state had been found. The vibration is once again synchronous and shows a concerted mechanism in the formation of the two new C-C sigma bonds.

Geometry of the Transition State

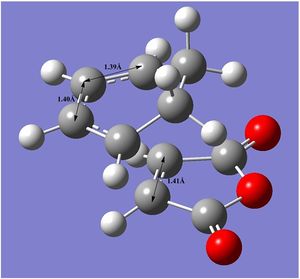
In forming the endo state, the double bonds of the cyclohexadiene is closer to the -(C=O)-O-(C=O)- fragment of the maleic anhydride whearas in the exo state, the double bonds of the cycloheadiene is on the far side relative to the maleic anhydride.

The bond distances and through space distances for both transition states were analysed and these are visualized in the tables down below. As stated previously, the bond length of a C(sp²)=C(sp²) double bond is 1.31-1.34Å and for a conjugated C(sp²)-C(sp²) bond it is 1.45-1.46Å. In both transition states, it can be seen that the double bonds involved in the reaction have lengthened to become more similar to a single bond whilst the single bond has shortened and is becoming more like a double bond.

Endo Transition State

Bond Distances	Through Space Distances

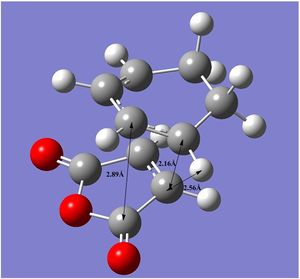
The Van der Waals radius of a carbon atom is 1.70Å. For the endo state, the through bond distances are longer than the radius but shorter than the sum of Van der Waals radii. The distances are of the same length on both sides of the molecule and thus it can be concluded that two new bonds are forming simultaneously in a concerted fashion.

Exo Transition State

Bond Distances	Through Space Distances

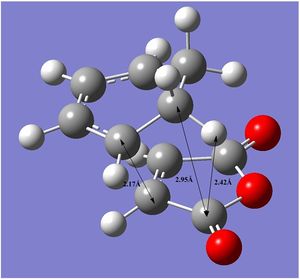
The through space distances between the carbon atoms are the same for both the endo and exo transition states. The only difference is the distance between the carbon on maleic anhydride and the nearby hydrogen on the cyclohexa-1,3-hexadiene which has a value of 2.56Å for the endo (Why is this particular distance important? Shouldn't it be similar for the exo transition state? João (talk) 18:57, 1 April 2015 (BST)) transition state and 2.42Å for the exo transition state. The exo state is should therefore be under more strain compared to the endo state and this can be seen by comparing their relative energies and it can be seen that the exo state is higher in energy compared to the endo state. The endo state is therefore formed faster and is the kinetic product.

Secondary Orbital Overlap

There has been much debate as to why the endo state is more stable compared to the exo state but it is now widely accepted to be due to secondary orbital overlap interactions present in the endo form which help to stabilize it. (References? What is the secondary orbital effect? João (talk) 18:57, 1 April 2015 (BST))

In order to understand these secondary orbital overlaps, the molecular orbitals of the reactants were visualized first to obtain the following:

Cyclohexadiene		Maleic Anhydride
HOMO	LUMO	HOMO	LUMO
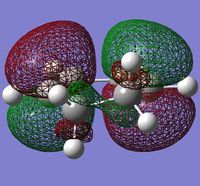
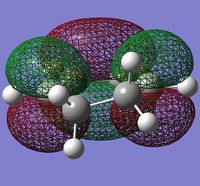
-0.44186au	-0.05948au	-0.32194au	+0.01680au
Antisymmetric	Symmetric	Symmetric	Antisymmetric

A plane of σ_v symmetry lies vertical to the plane of the molecule and the molecular orbitals are assigned symmetric or antisymmetric with respect to this plane (For cycloexadiene as you've drawn it, is there a plane of symmetry? João (talk) 18:57, 1 April 2015 (BST)). Maleic anhydride is an electron poor dienophile due to the presence of the electronegative oxygen and electron withdrawing carbonyl carbon atoms. On the other hand, cyclohexadiene is electron rich due to the presence of its many double bonds. Molecular orbitals of the same symmetry can interact and thus it is possible for the cyclohexadiene HOMO to interact with the maleic anhydride LUMO to get one transition state and the cyclohexadiene LUMO to interact with the maleic anhydride HOMO to get another transition state. (For the same transitions state, characterized by a given molecular structure, could not both orbital interactions be contribution to the energy? João (talk) 18:57, 1 April 2015 (BST))

Endo		Exo
HOMO	LUMO	HOMO	LUMO
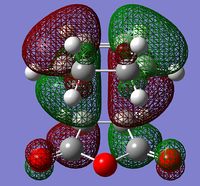
Antisymmetric

For both the endo and exo HOMO, it can be seen that they are antisymmetric to the σ_v plane of symmetry. Both HOMO are formed by the interactions between the cyclohexadiene HOMO and the maleic anhydride LUMO.

It has been proposed that additional secondary orbital overlap interactions are present within the endo state which helps to stabilize the overlap energy. These secondary orbital overlaps should be between the π orbitals of the carbonyl groups and the π orbitals at the back of the cyclohexadiene molecule. Only a small interaction can be seen for the endo HOMO (What should the reader be looking for? João (talk) 18:57, 1 April 2015 (BST)) so the effect should only be very minor.

The exo state is most likely to be higher in energy compared to the endo state due to steric effects caused by the close proximity of the carbonyl carbon atoms and the nearby hydrogen atoms on the cyclohexadiene as stated previously. This distance is shorter for the exo state than the endo state.

Conclusions

In this study, the transition structures for different reactions were generated and optimized using different levels of theory. The B3LYP/6-31G* method was found to give results that resembled experimentally obtained data the closest compared to HF/3-21G. Different methods of locating the transition state were tested and it was found that the QST3 method gave the best results in comparison to QST2 and the freeze coordinate method (Whay was it better? How was it different? João (talk) 18:57, 1 April 2015 (BST)), however, this method was also found to be the most expensive and time consuming.

The chair and boat transition states of the Cope rearrangement were calculated and it was found that the chair form had a lower energy and shows that the Cope rearrangement proceeds via this transition state.

The Diels-Alder reaction between cyclohexa-1,3-diene and maleic anhydride was also calculated and it was found that the endo form is lower in energy compared to its exo counterpart, and the reasons for this were thought to be due to the longer distance between the carbonyl carbons on maleic anhydride and the hydrogen atoms on the cyclohexadiene in the endo form. Secondary orbital overlap interactions were also thought to play a part in stabilizing the endo transition state but analysis of the molecular orbitals showed only very minor contributions from these in the endo state.

More experiments are required in order to test the true contribution of secondary orbital overlap to the endo transition state.