Rep:Mod:kl1111comp
Introduction: Inorganic Computational Chemistry
Computational chemistry uses computer simulation to predict the structure and properties of complexes. It is a necessary branch of chemistry due to its ability to differentiate the relative energies of stable conformers, in particular the transition states and intermediates which are otherwise impossible to characterize experimentally. Other properties which can be obtained using computational chemistry include dipole moments, vibrational frequencies and molecular orbitals and is widely used in the design of new drugs.
In the current study, BH3, BBr3 and GaBr3 were optimised using GaussView. From these optimised molecules, the vibrational frequencies and population levels were predicted.
Optimisation and Frequency analysis
The method and basis set is very sensitive and minor changes can change the total energy calculations drastically. Thus for a proper comparison between the optimisation and frequency, the same method and basis set must be used.
By conducting a frequency analysis, it is possible to find out whether the optimisation has worked. It is in essence, a second derivative of the potential energy diagram and thus can determine whether a minimum or transition state has been reached, and if neither has occured then optimisation has failed. In addition, the computed frequencies can be compared to values obtained experimentally.
Low frequencies represent a heavier molecule or weaker bond strength. It is possible to determine the identities of molecules within a series by analysis of their frequencies. Most frequencies occur within 15cm-1 of each other.
BH3
Optimisation: B3LYP/3-21G level
A trigonal planar BH3 molecule was created and the D3h point group was imposed upon it. It was then optimised using the B3LYP method and 3-21G basis set. The 3-21G basis set has a low accuracy but is calculated fairly quickly and was thus chosen to begin with.
Optimisation log file here
To check whether the optimisation had completed, the summary was observed for a gradient value less than 0.001 a.u. As observed, the gradient is significantly smaller than 0.001 but this was checked once more using a second method involving examination of the output file for complete convergence.
To observe what is occuring during optmisation, a total energy curve and root mean square gradient (RMS) graph were obtained. In the first graph, it can be seen that Gaussview is searching the potential energy surface (PES) of the BH3 molecule for a structure with minimal energy. As a minimum/maximum point is reached, it is expected that the derivative of PES should approach zero and thus the RMS gradient in the second graph is expected to reach zero. Confirmation of the minimum point can be done by frequency analysis, which will come later.
Optimisation: B3LYP/6-31G (d,p) level
Although the 3-21G basis set calculation is quick, it only provides an estimate for the structure of the optimised molecule due to its low accuracy. For this reason, BH3 was optimised once more using a higher basis set, 6-31G (d,p). To further improve accuracy, the keywords "scf=conver=9" were added to the Additional Keywords section, in addition to the default comments "integral=grid=ultrafine". This new command uses the trapezoidal rule to add more "strips" under the total energy curve and get a better estimate of the area.
Optimisation log file here
| summary data | convergence | Jmol | |||
|---|---|---|---|---|---|

|
Item Value Threshold Converged? Maximum Force 0.000010 0.000450 YES RMS Force 0.000006 0.000300 YES Maximum Displacement 0.000039 0.001800 YES RMS Displacement 0.000025 0.001200 YES |
|
Once again, complete optimisation was checked by analysis of the gradient and convergence in the output file. The obtained values show that optimisation had gone to completion.
Geometry Information
| Method | 3-21G | 6-31G (d,p) |
|---|---|---|
| B-H bond length (Å) | 1.19 | 1.92 |
| H-B-H bond angle (°) | 120.0 | 120.0 |
Frequency Analysis
As mentioned before, a frequency analysis was conducted on the BH3 optimised at the 6-31G (d,p) level to check whether a minimum point structure had been achieved.
Frequency file here
| summary data | low modes |
|---|---|

|
Low frequencies --- -14.1270 -12.1225 -10.2884 0.0003 0.0178 0.3550 Low frequencies --- 1162.9544 1213.1254 1213.1257 |
By analyzing the low frequencies displayed in the information box above, it can be seen that all of them are positive, and thus a minimum point has been obtained. All frequencies are within 15cm-1 of each other.
Vibrational Spectrum
| wavenumber | Intensity | IR active? | type | 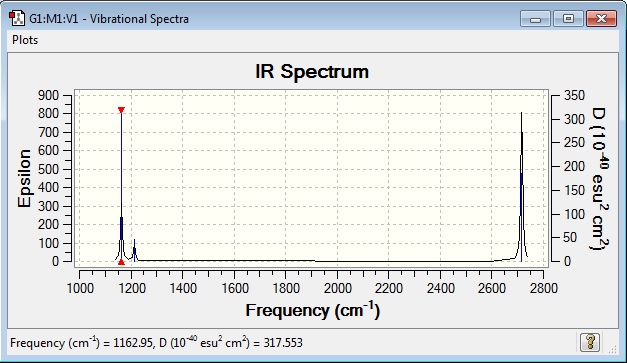
|
|---|---|---|---|---|
| 1163 | 93 | yes | bend | |
| 1213 | 14 | very slight | bend | |
| 1213 | 14 | very slight | bend | |
| 2582 | 0 | no | stretch | |
| 2716 | 126 | yes | stretch | |
| 2716 | 126 | yes | stretch |
Although there are six vibrational frequencies in BH3, only three can be observed in the IR spectrum due to degeneracy. The 2 bending frequencies observed at 1213 cm-1 are of the same energy and thus only a single peak can be observed. This is the same for the 2 stretching frequencies at 2716 cm-1. Th IR stretch at 2583 cm-1 is not observed due to the three equivalent bond stretches cancelling out any dipole moment.
GaBr3
Heavier atoms, especially those in the third row of the periodic table exhibit relavistic effects which cannot be recovered by the Shrodinger equeations. By using a psuedo-potential, it is possible to recover some of the relativistic effects and make the calcuations run faster and so the followng molecule was optimised using a different basis set to the one used in BH3.
Optimisation: B3LYP/LANL2DZ level
A molecule of GaBr3 was created and constrained to the D3 point group. It was then optimised using the LanL2DZ basis set. This basis set uses pseudo-potentials on heavier atoms and so applies to both Ga and Br.
Optimisation log file DOI:10042/136579
| summary data | convergence | Jmol | |||
|---|---|---|---|---|---|

|
Item Value Threshold Converged?
Maximum Force 0.000000 0.000450 YES
RMS Force 0.000000 0.000300 YES
Maximum Displacement 0.000003 0.001800 YES
RMS Displacement 0.000002 0.001200 YES
Predicted change in Energy=-1.307744D-12
Optimization completed.
-- Stationary point found.
|
|
As shown above, the gradient acheived was less than 0.001a.u and implied that the optimisation had gone to completion. To confirm this, the frequency analysis was carried out in order to find if the minimum energy structure had been achieved.
Geometry Information
| Ga-Br bond distance (Å) | 2.35 |
|---|---|
| Br-Ga-Br bond angle (°) | 120.0 |
The calculated Ga-Br bond distance was found to be 2.35Å. This is similar in value to the literature value of 2.249Å. [1]
Frequency Analysis
Frequency file here
| summary data | low modes |
|---|---|

|
Low frequencies --- -1.4877 -0.0015 -0.0002 0.0096 0.6540 0.6540 Low frequencies --- 76.3920 76.3924 99.6767 |
All frequencies were found to be within 15cm-1 of each other. All low frequencies are positive, indicating that a minimum energy structure had been found.
Vibrational Spectrum for GaBr3
| wavenumber | Intensity | IR active? | type | 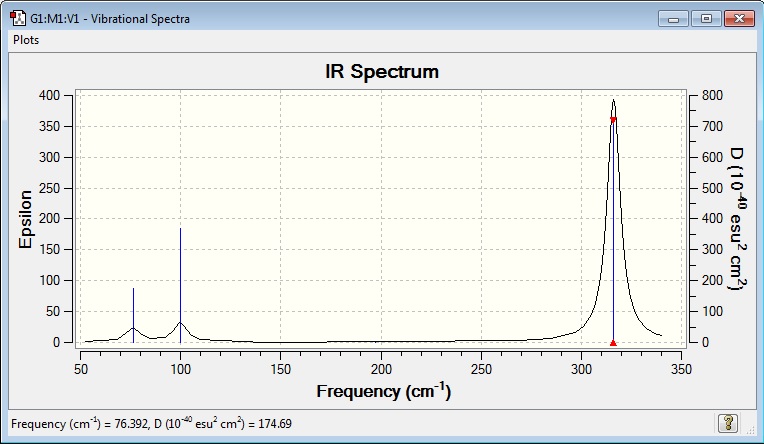
|
|---|---|---|---|---|
| 76 | 3 | very slight | bend | |
| 76 | 3 | very slight | bend | |
| 100 | 9 | very slight | bend | |
| 197 | 0 | no | stretch | |
| 316 | 57 | yes | stretch | |
| 316 | 57 | yes | stretch |
In a similar way to the BH3 molecule, only three of the six frequencies can be observed, once again due to degeneracy. The 2 bending frequencies at 76 cm-1 are both observed as a single frequency due to them having the same energy. The same explanation can be applied to the 2 stretching frequencies at 316 cm-1. The stretch at 197 cm-1 has no overall dipole moment and thus no peak can be observed.
Comparison of vibrational spectra of GaBr3 and BH3
When comparing the two IR spectra for BH3 and GaBr3, it can be seen that the frequencies observed in GaBr3 occupy much smaller frequencies, between 0 - 350 cm-1 compared to 0 - 3000 cm-1 in BH3. The difference in frequencies can be explained by Hooke's Law for a harmonic oscillator:
v=√(f/µ)/2πc
where v is the frequency, f is the force constant (bond strength) and µ is the reduced mass:
µ = (m1m2)/(m1+m2)
From this relationship between frequency and bond strength/reduced mass, it can be seen that for a GaBr3, it is heavier and has weaker bonds compared to BH3 and thus a smaller frequency is expected.
Upon inspection of the A2 "umbrella" vibration displayed by both GaBr3 and BH3, it can be seen that in both cases, the lighter atom is doing the moving. However, for GaBr3, it is the central Ga atom which is moving compared to the external hydrogen atoms in BH3.
The GaBr3 umbrella vibration occupies a much lower frequency at 100 cm-1 compared to the BH3 umbrella motion. Again, this can be explained by BH3 having a lower reduced mass and higher bond strength.
The intensity of IR peaks is related to the change in dipole moment during a bond stretch and the number of atoms present. For a large dipole moment, strong absorption is observed and a weak absorption for a small dipole moment. The GaBr bond is large and diffuse, corresponding to a weak bond and small dipole moment. This can be seen in the low intensities observed for GaBr3 compared to the higher intensities in BH3 due to the more compact bond and thus larger dipole moment.
BBr3
B3LYP/6-31G(d,p)LANL2DZ level
A BBr3 molecule was created and optimised with the Gen method. The 6-31G (d,p) basis set was applied to the boron atom whilst the LanL2DZ basis set was applied to the bromine atoms. A different basis set was applied to the bromine atoms due to them being heavier and hence requiring the use of pseudo-potentials.
Optimisation log file here
| summary data | convergence | Jmol | |||
|---|---|---|---|---|---|

|
Item Value Threshold Converged? Maximum Force 0.000009 0.000015 YES RMS Force 0.000006 0.000010 YES Maximum Displacement 0.000034 0.000060 YES RMS Displacement 0.000023 0.000040 YES |
|
The gradient was checked again for a low value to ensure optimisation had occured.
Geometry information
| B-Br bond distance (Å) | 1.93 |
|---|---|
| Br-B-Br bond angle (°) | 120.0 |
The calculated bond distance was found to be 1.93Å. This is comparable to the literature value of 1.893Å. [1] The bond angle is expected for a trigonal planar molecule.
Geometry Comparison
| BH3 | BBr3 | GaBr3 | |
|---|---|---|---|
| r(E-X) | 1.19 | 1.93 | 2.35 |
| θ(X-E-X) | 120.0 | 120.0 | 120.0 |
When comparing BH3 and BBr3, it can be seen that changing the ligand from hydrogen to bromine increases the bond length from 1.19Å to 1.93Å, an increase of 0.74Å. Hydrogen and bromine are similar in that they both donate a single electron to the centre atom to form a sigma bond. However, They differ greatly in size and thus their orbitals do not overlap well. Due to the large diffuse orbitals of bromine compared to hydrogen, the interaction between the boron orbital and the bromine orbital is not very good, leading to poor overlap, weaker interactions and a lengthening of the bond, when compared to the B-H bond.
When the ligand was kept constant as bromine, the central atom was changed from boron to gallium. The consequence of this is an increase in bond length from 1.93Å to 2.35Å, an increase of 0.43Å. In a similar way to the hydorgen/bromine comparison, it can be said that the boron and gallium atom both have three external electrons thus can contribute these electrons to make three sigma bonds. They differ only in the size of their atoms and thus the orbitals are also different in size, with gallium being the larger atom with larger, more diffuse orbitals.
A covalent bond can be defined as the sharing of two negatively charged electrons between two positively charged nuclei. These chemical bonds can be strong, medium or weak. However, covalent bonds are not the only bonds that exist, there are many others that exist, for example ionic bonds which is the donation of a pair of electrons from one atom to another, 3c-2e bonds etc.
An example of a strong bond is the C2 alkyne bond which has a bond strength of 839 kJmol-1, a medium bond as C=C with a bond strength of 614 kJmol-1 and a weak bond as O-O which has a bond strength of 145 kJmol-1. Even weaker bonds exist, such as the Ne-Ne bond which has a bond strength of 498kJmol-1 and would thus rather exist as a monoatomic atom.
On several occasions, Gaussview has not drawn in the bonds between atoms in optimised molecules. This does not suggest the non-existence of a bond, but that the bond length has exceeded a pre-determined value.
NH3
Optimisation: B3LYP/6-31G(d,p) level
A molecule of NH3 was created and constrained to the C3v point group. It was then optimised using the 6-31G basis set.
Optimisation log file here
| summary data | convergence | Jmol | |||
|---|---|---|---|---|---|

|
Item Value Threshold Converged? Maximum Force 0.000006 0.000015 YES RMS Force 0.000004 0.000010 YES Maximum Displacement 0.000012 0.000060 YES RMS Displacement 0.000008 0.000040 YES |
|
The gradient was checked for a value close to zero (which it is) and the .log file check for complete convergence to ensure optimisation had gone to completion.
Frequency file here
| summary data | low modes |
|---|---|

|
Low frequencies --- -0.0130 -0.0022 -0.0017 7.0722 8.1014 8.1017 Low frequencies --- 1089.3849 1693.9369 1693.9369 |
The frequencies are low and within 15cm-1 of each other and are all positive, indicating that a minimum energy structure had been found.
Vibrational Spectrum for NH3
| wavenumber | Intensity | IR active? | type | 
|
| 1089 | 145 | yes | bend | |
| 1694 | 14 | very slight | bend | |
| 1694 | 14 | very slight | bend | |
| 3461 | 1 | no | stretch | |
| 3590 | 0 | no | stretch | |
| 3590 | 0 | no | stretch |
Only two peaks are observed, despite there being six vibrations. The last three vibrations are of very low intensity so cannot be seen. The vibrations at 1694cm-1 are degenerate and thus only one peak can be observed for the two vibrational modes. That leads to there being one other peak at 1089-1 which has a change in dipole moment and can be observed under IR.
Population Analysis
A population analysis was carried out and the MO diagrams from the .chk file were obtained.

|

|

|

|
| MO1 | MO2 | MO3 | MO4 |
|---|---|---|---|

|

|

|

|
| MO5 | MO6 | MO7 | MO8 |
A NBO analysis was carried out on the NH3 molecule.
Population Analysis here: DOI:10042/144246
The nitrogen is negatively charged with respect to the three hydrogen atoms. This is to be expected since it is the more electronegative element and will therefore draw electron density towards itself.
1. (1.99909) BD ( 1) N 1 - H 2
( 68.83%) 0.8297* N 1 s( 24.86%)p 3.02( 75.05%)d 0.00( 0.09%)
( 31.17%) 0.5583* H 2 s( 99.91%)p 0.00( 0.09%)
2. (1.99909) BD ( 1) N 1 - H 3
( 68.83%) 0.8297* N 1 s( 24.86%)p 3.02( 75.05%)d 0.00( 0.09%)
( 31.17%) 0.5583* H 3 s( 99.91%)p 0.00( 0.09%)
3. (1.99909) BD ( 1) N 1 - H 4
( 68.83%) 0.8297* N 1 s( 24.86%)p 3.02( 75.05%)d 0.00( 0.09%)
( 31.17%) 0.5583* H 4 s( 99.91%)p 0.00( 0.09%)
As observed above, the nitrogen is contributing more towards the N-H bonds and shows that most of the electron density is located on the N atom. Charge Distribution file: here
Molecular Orbital of BH3
A population analysis was carried out on the BH3 molecule by running an energy calculation on the optimised 6-31G molecule.
 |
There is good comparison between the real and and LCAO MOs, suggesting that computational calculations are quite accurate.
NH3BH3
In order to calculate the association energy of ammonia borane, the energy of the reactants and products were calculated are needed. The energies of the ammonia and borane molecules have already been computed above.
Optimisation: B3LYP/6-31G(d,p) level
The NH3BH3 molecule was optimised using the B3LYP method and 6-31G basis set. The additional keywords "integral=grid=ultrafine scf=conver=9" were used throughout and used again here so that a valid comparison could be made between the three individual molecules. Complete optimisation was checked by analysis of the gradient and convergence of the displacements.
Optimisation log file here
| summary data | convergence | Jmol | |||
|---|---|---|---|---|---|

|
Item Value Threshold Converged? Maximum Force 0.000002 0.000015 YES RMS Force 0.000001 0.000010 YES Maximum Displacement 0.000034 0.000060 YES RMS Displacement 0.000010 0.000040 YES |
|
Frequency Analysis
This was calculated to ensure that the minimum energy structure had been found.
Frequency file here
| summary data | low modes |
|---|---|

|
Low frequencies --- -5.5535 -0.2640 -0.0380 -0.0013 1.4243 1.4792 Low frequencies --- 263.2922 632.9558 638.4634 |
Frequencies are all low and positive and thus a minimum point has been reached.
Population Analysis
Population Analysis File: DOI:10042/144884
The MO diagrams were obtained from the .chk file of the population analysis.

|

|

|

|

|
| MO1 | MO2 | MO3 | MO4 | MO5 |
|---|---|---|---|---|

|

|

|

|

|
| MO6 | MO7 | MO8 | MO9 | MO10 |
Nitrogen, being the most electronegative element present in the molecule is the most negatively charged. It draws electron density away from its neighbouring atoms, rendering the hydrogen atoms positively charged. The carbon is shown to be negatively charged, which is unusual since it is bonded to the nitrogen. This can be explained by carbon being more electronegative compared to hydrogen and so it draws electron density away from the hydrogen atoms and becomes negatively charged.
Bond Energies
| Molecule | E (a.u) |
|---|---|
| NH3 | -56.5577687 |
| BH3 | -26.6153236 |
| NH3BH3 | -83.2246891 |
Dissociation Energies
ΔE=E(NH3BH3)-[E(NH3)+E(BH3)]
ΔE= -83.2246891 - (-26.6153236-56.5577687) a.u.
ΔE= -0.0515968 a.u.
ΔE= -135.47 kJ mol-1
It was previously mentioned that a bond of energy ~150 kJmol-1 would be weak. The B-N bond is also of a similar magnitude so must therefore be weak.
Conclusion
BH3, BBr3, GaBr3, NH3 and NH3BH3 were all optimised to find a low energy structure and a frequency analysis was carried out to confirm that it had been reached. The computed frequency analysis gave a predicted IR vibrational spectrum for the molecules and could be used to predict and rationalise the wavenumber and intensity of a particular vibration bu use of the mass of the atom and their bond strengths. A population analysis was then carried out on BH3, GaBr3, NH3 and NH3BH3 and the output files were used to make further calculations such as MO and NBO. The LCAOs were similar to the real MOs, but it was found that this only really applied to the occupied MOs. The association energy of a bond could be calculated by use of the known energies of the reactants and products and this was applied to ammonia borane.
Throughout the experiment, the basis set and method were kept constant due to the total energy of a calculation being very sensitive and slight changes to any part of the experimental procedure could have affected the outcome.



