Rep:Mod:kkz161
Molecule 1: NH3
Optimisation (log. link)
Optimised NH3 molecule |
Calculation Method: RB3LYP
Basis Set: 6-31G(d,p)
Final Energy E(RB3LYP): -56.55776873 a.u.
RMS Gradient Norm: 0.00000485 a.u.
Point Group: C3V
Item Value Threshold Converged? Maximum Force 0.000004 0.000450 YES RMS Force 0.000004 0.000300 YES Maximum Displacement 0.000072 0.001800 YES RMS Displacement 0.000035 0.001200 YES
Propeties
N-H Bond Distance: 1.01798 Å
H-N-H Bond Angle: 150.741°
The bond distance agrees with the literature at 1.02Å while the bond angle is lower than the 107° found in the literature. [1] This is due to the hydrogen bonding which is not accounted for in this computing model as NH3 is taken to be an ideal gas.
Vibrations
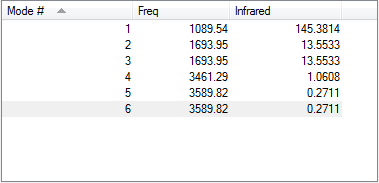
According to the 3N-6 Rules 6 modes should be observed (which is true as seen in the table above), however for NH3 modes 2 & 3 and 5 & 6 are degenerate pairs as seen by their identical energy values.
Modes 1,2 and 3 are bending vibrations with 1 being the umbrella mode while modes 4,5 and 6 are stretching vibrations with4 being the highly symmetric stretch. Due to the degeneracies observed in these modes, only 4 bands would be expected to be observed in an IR spectrum of ammonia.
Charge Distributions
It is expected that the nitrogen atom (N) will have a negative change distribution as it is (much) more electronegative than hydrogen and so draws a lot of negatively charged electron density towards it. Hydrogen will therefore be expected to have a positive charge 1/3 that of the nitrogen as the molecule as a whole is neutral and there are 3 hydrogens in identical environments, and they each loose the same amount of electron density to the nitrogen atom.
N: -1.125
H: 0.375
Molecule 2: H2
Optimisation (log. link)
Optimised H2 molecule |
Calculation Method: RB3LYP
Basis Set: 6-31G(d,p)
Final Energy E(RB3LYP): -1.17853930 a.u.
RMS Gradient Norm: 0.00012170 a.u.
Point Group: Dinfh
Item Value Threshold Converged? Maximum Force 0.000211 0.000450 YES RMS Force 0.000211 0.000300 YES Maximum Displacement 0.000278 0.001800 YES RMS Displacement 0.000393 0.001200 YES
Propeties
H-H Bond Distance: 0.74309 Å
Vibrations
Only 1 mode was observed at 4461.48 cm-1. It is not IR active it is a perfectly symmetrical stretch.
Charge Distributions
The 2 atoms are in the molecule are in exactly the same environment and are of exactly the same element resulting in equal charges and a charge difference of 0.
Molecule 3: N2
Optimisation (log. link)
Optimised N2 molecule |
Calculation Method: RB3LYP
Basis Set: 6-31G(d,p)
Final Energy E(RB3LYP): -109.52412867a.u.
RMS Gradient Norm: 0.00009335 a.u.
Point Group: Dinfh
Item Value Threshold Converged? Maximum Force 0.000162 0.000450 YES RMS Force 0.000162 0.000300 YES Maximum Displacement 0.000051 0.001800 YES RMS Displacement 0.000071 0.001200 YES
Propeties
N-N Bond Distance: 1.10555Å
Vibrations
Only 1 mode was observed at 2456.86 cm-1. It is not IR active it is a perfectly symmetrical stretch.
Charge Distributions
The 2 atoms are in the molecule are in exactly the same environment and are of exactly the same element resulting in equal charges and a charge difference of 0.
Molecular Orbitals

Reaction Energy of N2 + 3H2 -> 2NH3
E(NH3)= -56.55776873 a.u.
2*E(NH3)= -113.11553746 a.u.
E(N2)= -109.52412867a.u.
E(H2)= -1.17853930 a.u.
3*E(H2)= -3.5356179 a.u.
ΔE=2*E(NH3)-[E(N2)+3*E(H2)]= -0.05579089 a.u. = -146.48 kJ/mol
This is much larger than the stated literature value of −91.88kJ/mol. [2] This is due to there being a number of nitrogen molecules present when the literature value was found, and also the difference in behavior of real and ideal gases. This model of ammonia does not account for any hydrogen bonding or Van Der Waals forces which could only occur in extremely low pressures in reality, while the experimental values occur at room temperature and pressure so there factors would be observed.
Molecule 4: F2
Optimisation (log. link)
Optimised F2 molecule |
Calculation Method: RB3LYP
Basis Set: 6-31G(d,p)
Final Energy E(RB3LYP): -199.49825220 a.u.
RMS Gradient Norm: 0.00000007 a.u.
Point Group: Dinfh
Item Value Threshold Converged? Maximum Force 0.000000 0.000450 YES RMS Force 0.000000 0.000300 YES Maximum Displacement 0.000000 0.001800 YES RMS Displacement 0.000000 0.001200 YES
Propeties
F-F Bond Distance: 1.40298Å
Vibrations
Only 1 mode was observed at 1064.56 cm-1. It is not IR active it is a perfectly symmetrical stretch.
Charge Distributions
The 2 atoms are in the molecule are in exactly the same environment and are of exactly the same element resulting in equal charges and a charge difference of 0.
Molecular Orbitals
The electronic configuration of a fluorine atom in the ground state is 1s2,2s2,2p5. The 2 atoms in this diatomic molecule are the same element; it is homodiatomic, therefore the molecular orbitals (MOs) formed will be from the direct overlap of identical orbitals. The bonding axis is the z axis in the MOs observed below, resulting in the 2 2pz orbitals forming a sigma bond (and antibond) and 2px and 2py each forming pi bonding (and antibonding) orbital. The 1σg and the 1σ*u orbitals have a very low energy (-24.79731a.u. and -24.79724a.u. respectively) as the 1s electrons of both fluorine atoms are core electrons. The highet occupied molecular orbital(s) (HOMO) for this molecule is the 1π*g orbital while the lowest unoccupied molecular orbital (LUMO) is the 3σ*u orbital.

The sigma bond (MO) formed from the overlap of in-phase 2s orbitals of 2 fluorine atoms (-1.33651a.u.)

The sigma antibond (MO) formed from out-of-phase 2s orbitals of 2 fluorine atoms (-1.09051 a.u.)
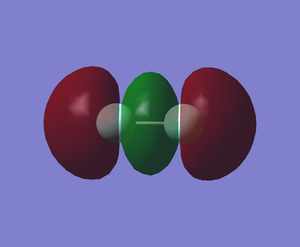
The sigma bond (MO) formed from the overlap of in-phase 2pz orbitals of 2 fluorine atoms (-0.58750 a.u.)

The pi bond (MO) formed from the overlap of in-phase 2px orbitals of 2 fluorine atoms (-0.52329 a.u.)

The pi antibond (MO) formed from the overlap of out-of-phase 2px orbitals of 2 fluorine atoms (-0.39193 a.u.)
