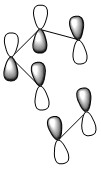
Rep:Mod:kkph1904
Module 3: Physical Computational Experiment
The Cope Rearrangement
In this part of the experiment, the Cope rearrangement of 1,5-hexadiene was analysed in Gaussian. The objectives of this part of the experiment were to find the low-energy minima and the transition states of this Cope rearrangement reaction, in order to determine the preferred reaction mechanism for the molecule.
Optimising the Reactants and Products
The 1,5-hexadiene molecule with an anti-periplanar conformation for central 4 carbons was drawn in GaussView. The structure was 'cleaned' and optimised using HF method and 3-21G basis set (LOG file). The .chk point was opened in GaussView to find out the energy and point group of the molecule. The energy of this conformation was -231.692535 Hartrees and the point group-Ci(two symmetry operations-E and i). The summary of results(from the LOG file not from the .chk file, but the energy is the same) is given below:
Filename = //ic.ac.uk/homes/kk2311/Desktop/Physical computational/cope rearrangement/trans/app/E app/COPE_STRUCTURE_OPT1_3-21G_E.LOG cope_KK_opt_3-21G_E File Name = COPE_STRUCTURE_OPT1_3-21G_E File Type = .log Calculation Type = FOPT Calculation Method = RHF Basis Set = 3-21G Charge = 0 Spin = Singlet E(RHF) = -231.69253516 a.u. RMS Gradient Norm = 0.00004313 a.u. Imaginary Freq = Dipole Moment = 0.0000 Debye Point Group = CI Job cpu time: 0 days 0 hours 0 minutes 20.0 seconds.
The same molecule but now with a gauche conformation for central 4 carbon atoms was drawn and optimised using HF/3-21G level of theory(LOG file). The energy of this conformation was -231.692661 Hartrees and the point group-C1(one operation-E). The summary of the results:
Filename = //ic.ac.uk/homes/kk2311/Desktop/Physical computational/cope rearrangement/gauche/KK_GAUCHE_STRUCTURE_3-21G_OPT1.LOG KK_gauhe_opt1_3-21G File Name = KK_GAUCHE_STRUCTURE_3-21G_OPT1 File Type = .log Calculation Type = FOPT Calculation Method = RHF Basis Set = 3-21G Charge = 0 Spin = Singlet E(RHF) = -231.69266122 a.u. RMS Gradient Norm = 0.00000493 a.u. Imaginary Freq = Dipole Moment = 0.3407 Debye Point Group = C1 Job cpu time: 0 days 0 hours 0 minutes 42.0 seconds.
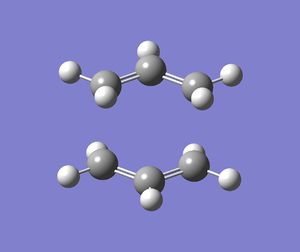
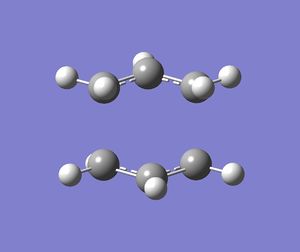
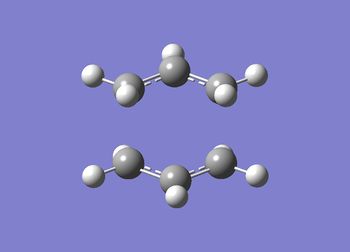
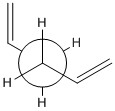
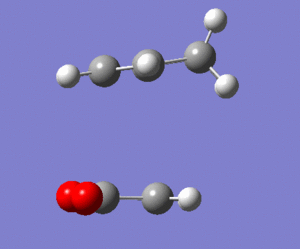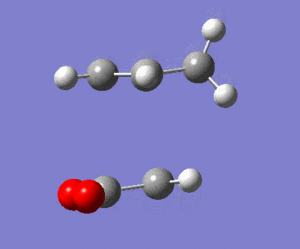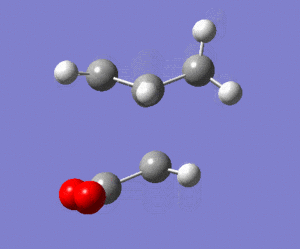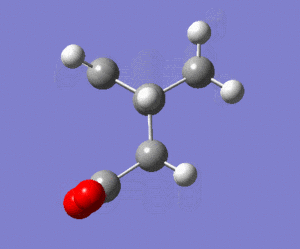
The calculated energy of the gauche conformation was lower than the energy of the anti-periplanar conformation. However, from the theoretical point of view, it could be that anti-periplanar conformation is preferred mainly due to smaller Pauli repulsion between the groups(torsional strain). Another important factor, the orbital overlap also between the groups also has to be considered. In gauche conformation there are two σ C-C/σ* C-H interactions, two σ C-H/σ* C-C interactions and two σ C-H/σ* C-H interactions. In anti-periplanar conformation there are four σ C-H/σ* C-H and two σ C-C/σ* C-C interactions. The total energy of these interactions of both conformations would determine which conformation is favoured by this factor. The σ C-H orbitals are higher energy donors than σ C-C, and also σ* C-C are lower energy acceptor than σ* C-H. So gauche could possibly be preferred by orbital orientation because now the σ C-H donation is possible in σ* C-C orbitals, which gives smaller σ-σ* gap and therefore larger stabilisation from the overlap. However, these are not the only interactions in molecule and both of these conformers have different number of specific orbital interactions(e.g. 4 σ C-H/σ* C-H in app, but only 2 in gauche). It could possibly be that orbital ineractions are very similar in energy for both of the conformers therefore the steric effect should be the dominant factor in this case as the energy of C-C and C-H orbitals is not large. The structures of both conformers are given below to illustrate this:
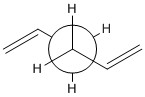 |
 |
The prediction from theory is that anti-periplanar conformation should be favoured over the gauche conformation, mainly because of the reduced steric interactions in anti-periplanar conformation. Also the information from the literature source[1] indicates that antiperiplanar conformations are favoured. There is not just one anti-periplanar conformation. The most stable conformation of 1,5-hexadiene is for the structure given on right. This conformation was also drawn in GaussView and was optimised using the same method-HF/3-21G. The energy of this app conformation was -231.692602 Hartrees and point group C2 (LOG). This energy is lower than the first anti-periplanar conformation but higher than the gauche one. This is not consistent with theory and prediction where anti-periplanar should be the favoured conformation. The reason could be that Hartree-Fock method was used which is the simplest calculation method and it includes no electron correlation so such factor as orbital overlaps are not properly considered. The summary of results is given:
Filename = //ic.ac.uk/homes/kk2311/Desktop/Physical computational/cope rearrangement/trans/app/B lowest/COPE_STRUCTURE_OPT1_3-21G_APP_LOWEST.LOG cope_KK_opt_3-21G_app_lowest File Name = COPE_STRUCTURE_OPT1_3-21G_APP_LOWEST File Type = .log Calculation Type = FOPT Calculation Method = RHF Basis Set = 3-21G Charge = 0 Spin = Singlet E(RHF) = -231.69260220 a.u. RMS Gradient Norm = 0.00004698 a.u. Imaginary Freq = Dipole Moment = 0.2027 Debye Point Group = C2 Job cpu time: 0 days 0 hours 0 minutes 5.0 seconds.
In order to really see whether the anti-periplanar conformation is favoured, better method and basis set were used(B3LYP/6-31G(d)) on all three conformations.
| Variables | Anti-periplanar(A) | Antiperiplanar(B) | Gauche | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Conformations |
|
|
| |||||||||
| Energy-HF/3-21G(Hartrees) | -231.692535 | -231.692602 | -231.692661 | |||||||||
| Energy-B3LYP/6-31G(d)(Hartrees) | -234.611705 (LOG) | -234.611783 (LOG) | -234.611329 (LOG) | |||||||||
| Point group | Ci | C2 | C1 | |||||||||
| Structure from Appendix 1 | anti2 | anti1 | gauche3 |
Optimisation and Frequency Analysis of Ci anti2 Conformation of 1,5-hexadiene(A)
This conformation of 1,5-hexadiene was optimised using better level of theory-B3LYP/6-31G(d). The energy of the conformer using this method(-234.611705 Hartrees) was lower compared to HF/3-21G(-231.692535 Hartrees).
The summary of the B3LYP/6-31G(d) calculations is given:
Filename = //ic.ac.uk/homes/kk2311/Desktop/Physical computational/cope rearrangement/6-31G/E app/COPE_STRUCTURE_OPT1_6-31G_E.LOG cope_KK_opt_6-31G(d)_E File Name = COPE_STRUCTURE_OPT1_6-31G_E File Type = .log Calculation Type = FOPT Calculation Method = RB3LYP Basis Set = 6-31G(d) Charge = 0 Spin = Singlet E(RB3LYP) = -234.61170487 a.u. RMS Gradient Norm = 0.00001308 a.u. Imaginary Freq = Dipole Moment = 0.0000 Debye Point Group = CI Job cpu time: 0 days 0 hours 1 minutes 5.0 seconds.
There are no obvious structural changes between the differently optimised structures. The energy was lower for the B3LYP/6-31G(d) optimised structure because the method and basis set are better than in HF/3-21G level of theory, therefore the structure closer to the real structure should be obtained using B3LYP/6-31G(d) level of theory. The structures with the corresponding energies(after optimisation) are given below:
| Variables | HF/3-21G | B3LYP/6-31G(d) | ||||||
|---|---|---|---|---|---|---|---|---|
| Structures |
|
| ||||||
| Energy (Hartrees) | -231.692535 | -234.611705 |
However, the angles and bond lengths were different in each case. This is summarised in the table:
| Variables | HF/3-21G | B3LYP/6-31G(d) | Literature values[2] |
|---|---|---|---|
| Average C=C bond length (Å) | 1.32 | 1.33 | 1.34 |
| Average C(H2)-C(H) bond length (Å) | 1.51 | 1.50 | 1.51 |
| C(H2)-C(H2) bond length (Å) | 1.55 | 1.55 | 1.54 |
| Average C-H bond length (Å) | 1.08 | 1.09 | 1.09 |
| C(H2)-C(H2)-C(H) angle (o) | 111.3 | 112.7 | 111.5 |
| C(H2)-C(H)=C(H2) (o) | 124.8 | 125.3 | 124.6 |
| C(H)=C(H2)-H (o) | 121.9 | 121.9 | 128.9 |
| C(H2)-C(H)-H (o) | 115.5 | 115.7 | 116.8 |
| H-C(H2)-H (o) | 116.3 | 116.5 | 112.0 |
As can be seen from the table above, the bond lengths and angles vary slightly between HF and B3LYP structures. Some of the bond distances(C=C, C-H) are longer for B3LYP structure than for HF, one(C(H2)-C(H)) is longer in HF but the middle(C(H2)-C(H2)) bond is the same length in both cases. The angles vary only slightly. The biggest difference is for C(H2)-C(H2)-C(H) angle which is wider in B3LYP structure. The C(H2)-C(H)-H angle was the same in both structures(to the significant figures given). All the values are also very similar to the literature values. Overall, the bond distances of B3LYP structure are more similar to literature values compared to HF structure. However, there is smaller difference between literature and HF structure angles than there is between B3LYP and literature values. There is a significant difference between literature and computed values of C(H)=C(H2)-H angle. As a result the H-C(H2)-H angle values are also quite different because this angle is dependent on the C(H)=C(H2)-H angle.
The calculated energies of the HF/3-21G and B3LYP/6-31G(d) structures were significantly different because different method and basis set were used. The angles and bond lengths didn't vary a lot between the differently optimised structures and the values are very similar to the literature values.
In the optimisation the forces that act on a molecule are calculated(gradients on potential energy surface). When the forces and the displacements converge(gradient on surface=0), that means that stationary point has been found. But his stationary point could correspond to global or local minimum, or even can be a saddle point(transition state). The frequency analysis is used to distinguish between the saddle point from other minimum points. For the minimum point all the real frequencies should be positive and real.
The frequency analysis(using B3LYP/6-31G(d)) was carried out for the 1,5-hexadiene(A). The molecule was symmetrised before the frequency analysis. The LOG file can be found here. The summary is given below:
Filename = //ic.ac.uk/homes/kk2311/Desktop/new anti 2/COPE_STRUCTURE_FREQ_6-31G_E_SYM.LOG KK_freq_E_sym File Name = COPE_STRUCTURE_FREQ_6-31G_E_SYM File Type = .log Calculation Type = FREQ Calculation Method = RB3LYP Basis Set = 6-31G(d) Charge = 0 Spin = Singlet E(RB3LYP) = -234.61171021 a.u. RMS Gradient Norm = 0.00001402 a.u. Imaginary Freq = 0 Dipole Moment = 0.0000 Debye Point Group = CI Job cpu time: 0 days 0 hours 2 minutes 20.0 seconds.
The energy after frequency analysis was lower compared to the one after optimisation because frequency analysis further improves the structure(the molecule was also symmetrised).
42 real frequencies were found and they all were positive(all the positive frequencies can be viewed here). The low frequencies from the analysis are shown:
Low frequencies --- -9.4947 -0.0007 0.0003 0.0005 3.6986 13.3737 Low frequencies --- 74.2639 80.9813 121.4052
The top line represents the rotational and translational energies but the bottom line are the 3 lowest real vibrational frequencies and these ones have to positive for the minimum point. If one of them would be negative(imaginary) that would correspond to the transition state.
The IR spectrum also was simulated:
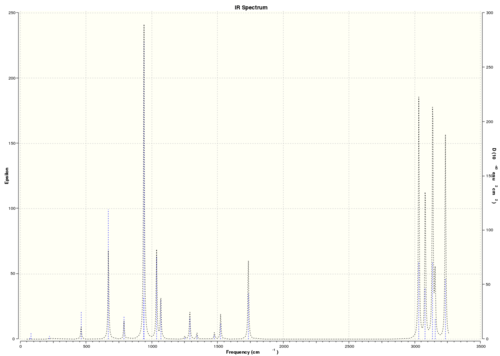
The thermodynamic properties also can be found in the output file:
Zero-point correction= 0.142507 (Hartree/Particle) Thermal correction to Energy= 0.149853 Thermal correction to Enthalpy= 0.150797 Thermal correction to Gibbs Free Energy= 0.110933 Sum of electronic and zero-point Energies= -234.469203 Sum of electronic and thermal Energies= -234.461857 Sum of electronic and thermal Enthalpies= -234.460913 Sum of electronic and thermal Free Energies= -234.500778
The following energies were found:
- E(at 0K) = Eelec + ZPE = -234.469203 Hartrees;
- E(at 298.15 K,1 atm) = E + Evib + Erot + Etrans = -234.461857 Hartrees;
- H = E + RT = -234.460913 Hartrees;
- G = H - TS = -234.500778 Hartrees.
The sum of electronic and thermal energies/enthalpies are larger compared to the sum of electronic and ZPE and the molecule is destabilised. The thermal energy excite electrons which occupy higher energy quantum levels therefore they have larger energy compared to the ground state. The sum of electronic and thermal free energies is the smallest and is mostly affected by positive entropy.
All these energies would be the same at 0 K and they all would be equal to E(at 0K) = Eelec + ZPE, where ZPE is a zero point energy ( a quantum mechanical energy which molecules posses even at 0 K). When calculations were carried out at 0 K, the Gaussian for some reason calculated the same energies as the ones given above. However, at 0.1 K the Gaussian calculated the energies and the magnitude of them was very similar(LOG).
Sum of electronic and zero-point Energies= -234.469203 Sum of electronic and thermal Energies= -234.469202 Sum of electronic and thermal Enthalpies= -234.469202 Sum of electronic and thermal Free Energies= -234.469203
The sum of electronic and ZPE energies have the same values when calculated at 0 K or 298.15 K because this sum of energies corresponds to the energy which molecule possess at 0K. The sum of electronic and thermal energies/enthalpies is very slightly larger than the sum of electronic and ZPE energies because of the minimal thermal excitation. The sum of electronic and thermal free energies is the same as the sum of electronic and ZPE energies.
Optimising the Chair and Boat Transition Structures
Optimisation of the Chair Transition State
Firstly, an allyl group (CH2CHCH2) was drawn in Gaussview and was optimised using HF method and 3-21G basis set. The LOG file can be found here. The optimised structure was then used to make something similar to the chair transition state for this cope rearrangement reaction. Two of these fragments were moved and rotated until their relative orientation was like the chair transition state. The distances between the terminal ends of the allyl fragments were 2.20 Å. Both of these structures can be viewed below:
 |
 |
This guess TS structure was then optimised using two different methods.
Method 1: The optimisation to a TS(Berny) with keywords Opt=NoEigen
The TS guess structure was copied into a new window. Opt+Freq was selected for the job type and the structure was optimised to a TS(Berny). The level of theory for this optimisation was HF/3-21G and additional keywords were added-Opt=NoEigen(LOG file). The energy of the chair TS was -231.619322 Hartrees and the point group after symmetrisation was C2h(from C1).
One negative imaginary frequency was observed at -818 cm-1 for this structure which corresponds to the structure being in the TS. The TS chair structure and the animation of the vibration are shown:
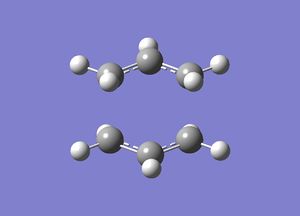 |
 |
As can be seen in the animation the terminal carbons on either side vibrate towards each other. When carbons on one side move closer, the carbons on the other side move further apart. This corresponds to the bond forming/breaking processes in the Cope rearrangement reaction.
Method 2: The optimisation using frozen coordinate method
The guess TS structure was copied into a new Gaussview window. The Redundant Coordinate Editor was then used to set the distance to 2.20 Å between the terminal carbons on both ends. Then these coordinates were frozen and the structure was optimised to a minimum using HF method and 3-21G basis set(LOG file).
The resulting optimised structure had fixed bond breaking/forming distances between the terminal carbons because the coordinates were frozen. These 'bonds' between the terminal carbons were optimised(TS-Berny) further by differentiating the coordinates between the terminal carbons(LOG file).
As can be seen, the structure on left has normal double bonds because this was optimised to the minimum with frozen coordinates. The structure on right is more like a TS because now the the bonds don't have normal double bond character and they are delocalised. The central C-C bond lengths also show this because the C-C bond length for the structure on right is longer than for the structure on left. The bond forming/bond breaking bond lengths are also different;this bond length for the structure on right is shorter compared to the structure on left.
The table which compares the two methods is given below:
Both methods give the same central and terminal bond distances which means they both work equally good for the optimisation of the chair transition state. The shapes of molecules also look very similar.
Optimisation of the Boat Transition State
In this part of the computational experiment the boat TS was optimised using the QST2 method. The products and reactants have to be specified for this method in order to find the TS.
The optimised anti2 structure was used to 'form' the reactant and the product for this Cope rearrangement reaction. For this method to work, the atoms in the product and reactant were numbered because the bond connections between the atoms in the reactant and product differered and this helped the program to identify between which atoms the bonds were made or broken.
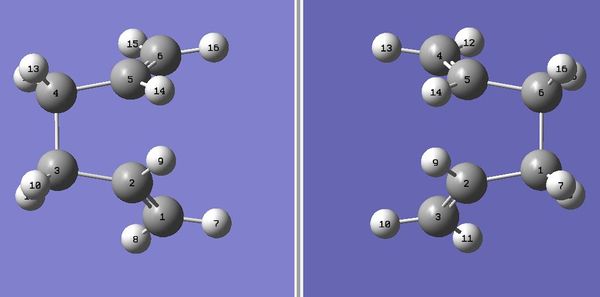
The anti2 molecule was copied twice into the GaussView window so that both of them could be viewed simultaneously. The atoms of the structures were then numbered so that the reactant and product numbers match the rearrangement reaction.

The resulting arrangement of anti2 molecules was optimised using the following method-Opt+Freq, TS (QST2), HF and 3-21G (LOG file). The optimised structure is shown:
As can be seen, the structure above looks very similar to the chair conformation. It doesn't look like a boat because the rotations around the central bonds weren't considered in this optimisation. In order to obtain boat like transition state structure, the reactant and product structures were modified-the angle of the central four C atoms was set to 0o and the angles C2-C3-C4(reactant), C3-C4-C5(reactant), C2-C1-C6(product) and C1-C6-C5(product) were set to 100o.
The optimisation was run again using the same method as in the first optimisation(LOG file). The energy of this boat TS was -231.602802 Hartrees and the point group C2v(after symmetrisation). One imaginary frequency was observed which frequency was -840 cm-1.
 |
 |
The vibrations in the boat TS correspond to the bond formation between the two pairs of terminal carbons. The vibrations are concerned-when one pair of terminal carbons approach each other, the other pair moves further apart. The vibrations in this TS are symmetric with respect to two pairs of terminal carbons and there is no preference between which two terminal carbons the bond will form.
Intrinsic Reaction Coordinate method
The IRC method allows to see the structural changes of a molecule by following the minimum path from a TS structure to the local minimum point. This method was applied to the boat and the chair TS structures. It can also help to identify which of the many conformers the boat and the chair transition states connect. The boat and chair TS structures are shown below in a Newman projection. The initial guess could be that the chair TS could lead to one of the many gauche conformations. The boat TS is in an eclipsed conformation which is a high energy conformer and most probably wouldn't lead to high energy eclipsed product molecule. The closest, most stable conformer which resembles the boat TS could also be the gauche conformer. However, there are many possible gauche conformations and to find out which gauche conformers are formed via the both transition states, the IRC analysis was carried out.
 |
 |
The chair transition state
The IRC method was first used on the chair transition state. The job type used: IRC -> Forward only -> Calculate always -> Compute more points, N=50. The level of theory used-HF/3-21G. Number of points along the IRC was changed to 50 because the default(10) wouldn't be enough to reach the local minimum structure.
The IRC calculations finished in 44 steps(LOG file). The energy of the final (44th) structure was -231.691579 Hartrees; the point group-C2(after symmetrisation).
 |
 |
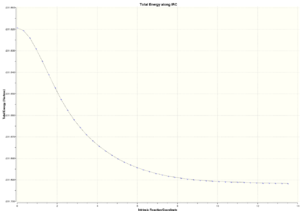 |
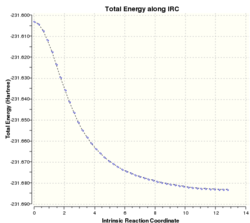
In the animation shown above, it can be seen how the bond forms between the two fragments. Then the molecule distorts to obtain the optimum angles and distances between the atoms(equilibrium bond distances). The distortion also minimises the repulsion between the atoms in the molecule. The image on the far right shows how the IRC analyis proceeded. The energy of the structures decreases smoothly until the lowest energy structure is obtained(gradient=0).
The final structure is very similar to the gauche2 structure(from Appendix 1) and they have the same point group(C2). The energy values are very slightly different. The energy of this structure is slightly higher(-231.691579 Hartrees) than the value given in the Appendix 1(-231.69167 Hartrees). This could be because the lowest energy structure wasn't found in the IRC analysis. To find the minimum energy conformation, the final(44th) structure was optimised to a minimum using HF/3-21G level of theory(LOG file). The energy of the resulting structure was -231.691667 Hartrees which now matches the energy of the gauche2 conformer from the Appendix 1(the point groups also match-C2).
So the chair TS connects the gauche2 conformers. As the reaction coordinate is symmetric, the reactants and products should be same conformer.
The boat transition state
The IRC analysis was also carried out for the boat TS structure. The same job type and method were used as in the previous example (with 50 steps). The IRC calculations finished in 45 steps. However, the energy of the resulting(45th) structure(-231.682981 Hartrees) was much larger than the energies of all other conformations given in the Appendix 1. This could be because the structure was in eclipsed-high energy conformation. The point group was Cs which is not the point group of any other conformers.
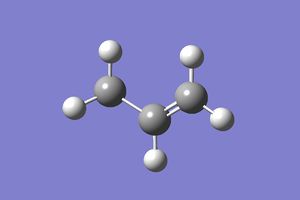 |
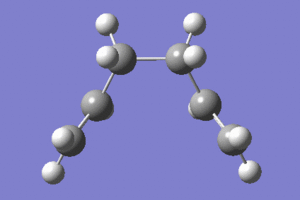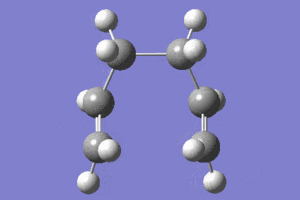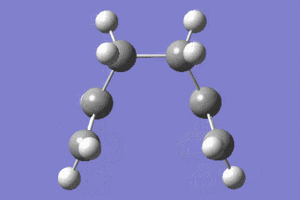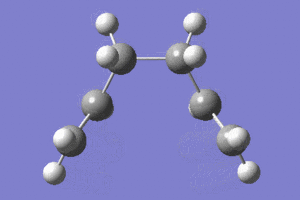 |
 |
In the animation it is shown how the bond forms between the terminal carbons on one side of the two fragments. The molecule than distorts symmetrically remaining in the eclipsed conformation. This agrees with the initial prediction that the eclipsed conformer could be formed.
In order to find a lower energy structure, the number of steps was increased from 50 to 100 and the IRC analysis was carried out again. This time the gauche conformer was found(in 72 steps). The energy of this conformer was -231.692613 Hartrees and the point group-C1. The energy of this conformer nearly matches the energy of the gauche3 conformation given in Appendix 1. They also have the same C1 point group.
 |
 |
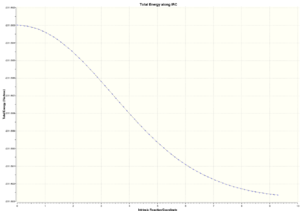 |
The second IRC analysis basically just distorted the molecule to obtain lower energy conformation. There is mainly rotation around the central C-C bond from high energy eclipsed(high torsional strain between groups; dihedral angle 0o) to lower energy gauche conformation(lower repulsion; dihedral angle 60o).
The final(72th) structure was further optimised using HF/3-21G level of theory to obtain even more stable structure(LOG). The shape of the structure didn't change significantly during optimisation and was essentially as the 72th structure. The energy of the optimised structure is -231.692661 Hartrees(point group C1) which is the same as for gauche3 conformation(point group C1). The shapes of the structures are also very similar.
Initially the eclipsed product was obtained via the the boat TS. When the number of steps was increased from 50 to 100, the gauche 3 conformer was obtained as the product molecule, therefore the boat TS connects gauche3 conformers.
The Activation energies
In order to get the activation energies via the boat and chair TS, the energies of the reactants and the TS have to be calculated. In the previous parts of this experiment, the chair and boat TS geometries were optimised using HF/3-21G level of theory but this level of theory is low. To obtain more reliable energy values (closer to literature values), the optimisation and frequency analysis was repeated for boat and chair transition states using better basis set and method-DFT/B3LYP/6-31G(d). The chair and boat transition states were optimised using Opt+Freq job type(LOG chair, LOG boat). As the boat TS was obtained by the anti 2 conformer, the energies of the TS were compared to energy of anti 2 conformer (reactant). In order to get reliable and comparable relative energies, the energies have to be compared relative to the same starting point. The reactant (anti2 conformation) was optimised using the same method and basis set as the chair and boat transition states(anti2 LOG files: HF LOG, B3LYP LOG). The three structures are compared in the table below:
The structures given above are from B3LYP/6-31G(d) frequency analysis and structurally they look very similar to HF/3-21G optimised structures. The same point group was obtained for the conformers using both levels of theory. However, the bond lengths vary between the HF/3-21G and B3LYP/6-31G(d) optimised structures.
The central C-C bond length in anti2 conformer is 1.55 Å in both cases. The HF optimised C(H2)-C(H) bond length is only 0.01 Å longer than the bond optimised by B3LYP/6-31G method. The opposite is true for the C(H)=C(H2) bond, where this bond is longer for B3LYP/6-31G level of theory.
The chair TS has C2h point group which was obtained by both methods. As can be seen in the table, there is slightly larger deviation for bond lengths in chair TS than there is in anti2 conformer. Slightly shorter distance between terminal carbons was obtained by B3LYP/6-31G(d) method - 0.05 Å shorter than using HF/3-21G method. The C(H2)-C(H) and C(H)=C(H2) bond lengths are the same in the chair TS because the bonds don't have a normal single, double characters and they are more delocalised. This can also be observed in the values from the table, where anti2 conformation C(H2)-C(H) bond is longer than the corresponding chair(and also boat) bond and anti2 conformer C(H)=C(H2) bond is shorter than bond in the chair(and boat) TS. The C(H2)-C(H) bond optimised by B3LYP/6-31G(d) method are only 0.02 Å longer than the bond optimised by HF/3-21G method.
The chair TS was also optimised by the two methods and the same C2v point group was obtained in both cases. The distance between the terminal carbons is 0.07 Å larger in B3LYP/6-31G(d) optimised structure and that is the largest difference in these series. The C(H2)-C(H) bond distances differ only by 0.01 Å between the two methods.
Overall, the geometries of the structures are very similar and the bond lengths differ only slightly between the two levels of theory. The biggest difference in bond lengths comes from the distance between the terminal carbons.
In the LOG file under the title 'Thermochemistry' ,different energies can be found for the structures. These energies and the total electronic energies from the summary files are summarised below:
| Structures | HF/3-21G electronic energy (Hartrees) | HF/3-21G sum of electronic and zero-point energies at 0K (Hartrees) | HF/3-21G sum of electronic and thermal energies at 298.15K (Hartrees) | B3LYP/6-31G(d) electronic energy (Hartrees) | B3LYP/6-31G(d) sum of electronic and zero-point energies at 0K (Hartrees) | B3LYP/6-31G(d) sum of electronic and thermal energies at 298.15K (Hartrees) |
|---|---|---|---|---|---|---|
| Anti2 conformer | -231.692535 | -231.539539 | -231.532566 | -234.611710 | -234.469203 | -234.461857 |
| Chair TS | -231.619322 | -231.466700 | -231.461341 | -234.556983 | -234.414929 | -234.409009 |
| Boat TS | -231.602802 | -231.450928 | -231.445299 | -234.543093 | -234.402343 | -234.396008 |
The activation energies can be calculated by subtracting reactant energy from the corresponding TS energy. The Ea can be calculated at 0K and at 298.15 K. The table which summarises the Ea energies via chair and boat transition states is given below(the energies are given in kcal/mol; 1 Hartree = 627.509 kcal/mol):
| TS | ΔEa HF/3-21G at 0K (kcal/mol) | ΔEa HF/3-21G at 298.15 K (kcal/mol) | ΔEa B3LYP/6-31G(d) at 0 K (kcal/mol) | ΔEa B3LYP/6-31G(d) at 298.15 K (kcal/mol) | ΔEa experimental at 0 K (kcal/mol) |
|---|---|---|---|---|---|
| Chair TS | 45.71 | 44.69 | 34.06 | 33.16 | 33.5±0.5 |
| Boat TS | 55.60 | 54.76 | 41.96 | 41.32 | 44.7±2.0 |
As can be seen in the table, the ΔE values via the chair TS are lower compared to the boat TS. This means that kinetically the reaction is more favourable via the chair TS where lower energy is needed to overcome the activation barrier.
Smaller ΔE energy values were obtained by B3LYP/6-31G(d) method and these energies are also very similar to the experimental values. The DFT/B3LYP/6-31G(d) method better describes the electron behavior in the molecule because it uses larger basis sets(a set of wave functions) and density functional theory which can give energies closer to the real values. The Hartree-Fock method is the simplest method(does not treat electron correlation exactly;uses average potential values) and 3-21G is lowe basis set than 6-31G. Another trend is that at higher temperature the ΔE gap becomes smaller and is because the molecule already possesses some thermal energy so less energy is needed to overcome the activation barrier.
The calculated ΔE energies at 0 K are very similar to the experimental values. For the chair TS the calculated value(33.16 kcal/mol) is within the region of the experimental values(33.5±0.5). There also is an error associated with the calculated energy by Gaussian and is about 2.39 kcal/mol. The ΔE energy at 0 K via the boat TS is also very close to the experimental values. If the error in experimental value is considered, the calculated value is not within the interval of experimental values. However, if the error in calculated energy is also considered, then the energies could possibly be very similar.
Overall, the calculated and experimental values at 0 K are very similar and the method(DFT/B3LYP/6-31G(d))used in this computational experiment is very reliable for calculating ΔE values for this Cope rearrangement reaction. The small difference between the computed and experimental values could be due to approximations used in the calculations,e.g., Born-Oppenheimer approximation.
The Diels Alder Cycloaddition
In this part of experiment the transition states of two cyloaddition reactions were located, optimised and analysed. The molecular orbitals of these TS were also visualised and analysed. The HOMO and LUMO were also visualised for cis butadiene.
HOMO and LUMO of cis butadiene
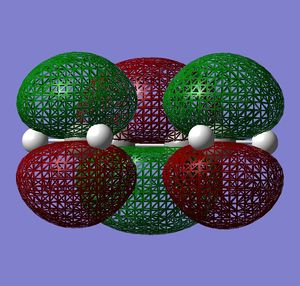
A molecule of cis-butadiene was drawn in GaussView and was optimised to a minimum using semi-empirical AM1 and HF/3-21G methods. The HOMO and LUMO orbitals were visualised by displaying the surface. The MO's are shown in the table:
| MOs | Semi-Empirical AM1(LOG) | HF/3-21G (LOG) | LCAO approach |
|---|---|---|---|
| LUMO | 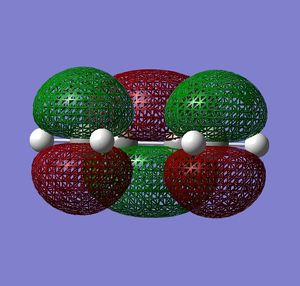 |
 |
 |
| HOMO | 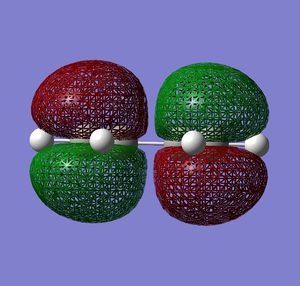 |
 |
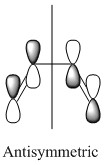 |
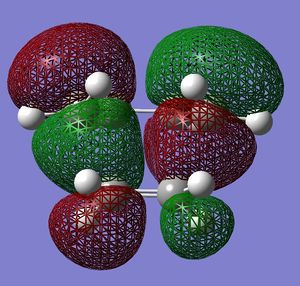
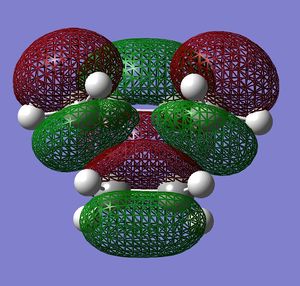
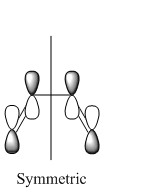
Very similar HOMOs and LUMOs were obtained by both methods. The shape of these molecular orbitals indicates that they are formed by overlap of C p AOs. Another indication that these MOs are former by p orbitals is that there are nodes at the center of C atoms which is characteristic for p orbitals. Nodal planes are going through all the carbons too. The MOs formed by the linear combination of atomic orbitals are shown in the column 'LCAO approach' (a very convenient way to represent AO contribution towards MO).
The symmetry of the MOs with respect to the plane can be determined by comparing the phases of p orbitals on both sides of the plane. The plane is drawn in the column 'LCAO approach' and this plane also persists in the computed MOs. The AOs on either side of the plane have to be considered together(as a whole) when comparing the both sides. It can be seen that in the LUMO the phases of AOs on either side of the mirror plane are the same so this MO is symmetric with respect to plane. In the HOMO the phase of AOs changes with respect to the plane therefore this MO is antisymmetric with respect to the plane. (NOTE: The symmetry plane is perpendicular to the screen and the drawn carbon atoms are in the plane which is parallel to the plane in which the carbons from computed MOs lie.)
Computation of the Transition State Geometry for the Diels Alder Reaction and an Examination of the Nature of the Reaction Path
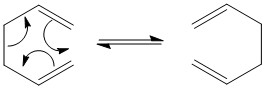
In this part of experiment, the cycloaddition reaction between cis-butadiene and ethylene was investigated. The reaction mechanism including TS is shown:
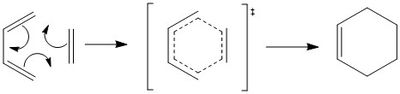
Cycloaddition reaction is one category of pericylic reactions where two or more σ bonds are made or broken in cyclic concerted transition state(no intermediates). This specific reaction is 6 electron process and can be specified as π4s + π2s cycloaddition reaction. It is thermally allowed because it has 6 electrons(4n+2) in the TS(aromatic TS).
Optimising the TS
At first, the TS geometry had to be located and optimised. To find the starting geometry of the TS, the cyclohexene product was drawn and the -CH2-CH2- fragment from this molecule was deleted. Then the ethylene was added close to the remaining fragment so that distance between the terminal carbons of both fragments was about 2.20 Å. The resulting guess TS structure was then optimised by two different methods to test which works better for this TS. The first method required to select Opt+Freq and optimise to a TS Berny(Calculate force constants once, and keywords Opt=NoEigen). The second method was the frozen coordinate method where int the first step bonds between the terminal carbons were frozen and the rest of the structure optimised to a minimum, but in the second step the structure was optimised to a TS(Berny). AM1 semi-empirical level of theory was used for both of these optimisations.
The guess TS structure was optimised successfully by both methods(Files: LOG file and summary of the first method; LOG file and summary of the second method). The obtained TS structure in both cases looked very similar. The TS structure from the first method is shown below:
 |
 |
 |
As can be seen in the images above, the terminal carbons between the two fragments point towards each other which means that orbital overlap between these carbons are maximised in this way. This will be later discussed in the molecular orbital section. The vibrations also correspond to the TS on the reaction path because the terminal carbons from both fragments vibrate towards each other in a synchronous motion which resembles the formation of the bonds.
The table below summarises the data from both methods. The obtained numbers indicate that both methods work very similarly.
| Method | Bond length between the fragments in the TS (Å) | Imaginary frequency (cm-1) |
| TS Berny (calculate force constant) | 2.12 | -956 |
| Frozen coordinate | 2.12 | -956 |
To further improve the the TS structure, the TS was optimised by HF/3-21G(LOG) level of theory followed by DFT/63LYP/6-31G(d) level of theory(LOG). As both of the optimised strutures structurally are very similar in shape, only the resulting TS structure from DFT/63LYP/6-31G(d) method's output file is shown.
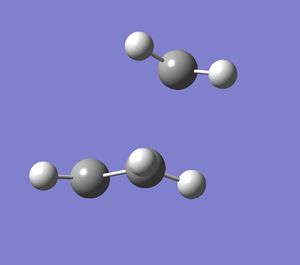 |
|
This optimised TS structure looks also very similar to the one optimised by AM1 method. The distances between the terminal carbons are also shown in the model above. These distances correspond to the forming σ bond distances in the TS. The table below shows the important information about the transition state obtained from the GaussView(the lowest positive frequencies are also shown).
| Method | Bond length between the fragments in the TS (Å) | Imaginary frequency (cm-1) | Lowest positive frequency (cm-1) |
| HF/3-21G | 2.21 | -818 | 167 |
| DFT/63LYP/6-31G(d) | 2.27 | -525 | 136 |
The bond lengths shown above are slightly different because they were obtained by two different methods. These bonds are also longer compared to the one obtained by AM1 method. As a result of different bond lengths between the terminal carbons, the imaginary frequencies also vary between the methods-shorter bonds are stronger(larger force constant) and have larger frequency. This is consistent with the results where the largest frequency (in magnitude) is for the shortest bond.
The length of the forming bonds between the fragments is about 2.27 Å (shown as 2.21 Å in the molecular model). The typical covalent C-C bond is about 1.54 Å, C=C bond is 1.34 Å and the Van der Waals radius of C is 1.70 Å. The Van der Waals radius(hard sphere) can be defined as a half of the distance of the closest approach between two non-bonded atoms of the same element. The distance between the terminal carbons in the TS is much larger compared to the covalent single and double bonds of C which means that this 'bond' is not covalent but is most probably an interaction. The sum of Van der Waals radii of two carbon atoms is about 3.40 Å. which tells us that the forming bond(2.27 Å) length distance in magnitude is between the the covalent bonds(C-C,C=C) and the sum of van der Waals radii. This means that the forming bonds could most probably be described as interactions between the carbon atoms rather than bonds. This interaction lies within the region where the orbitals of reacting species can interact attractively..[3]
If one negative(imaginary) frequency is obtained in normal optimisation(to the minimum) and frequency analayis, this means that TS has been found. As can be seen in the table above, one imaginary frequency was also obtained for this TS. In this case the imaginary frequency corresponds to the vibrations which are responsible for the reactive path. A TS is a saddle point which means it must have zero gradient on the potential energy surface and forces and displacements should converge at this point. The table which shows that they converged is shown(from DFT/63LYP/6-31G(d) calculations):
Item Value Threshold Converged?
Maximum Force 0.000041 0.000450 YES
RMS Force 0.000010 0.000300 YES
Maximum Displacement 0.001252 0.001800 YES
RMS Displacement 0.000279 0.001200 YES
Predicted change in Energy=-9.061869D-08
Optimization completed.
-- Stationary point found.
Both of the factors mentioned before are good indicators that TS was really found. Another way to illustrate that the TS has been found is to animate the vibrations of the imaginary frequency.
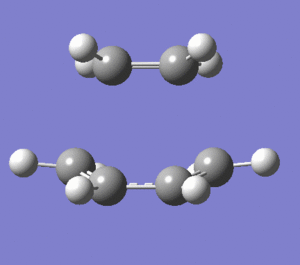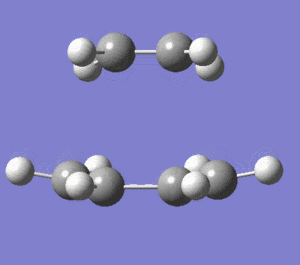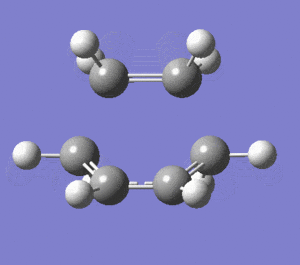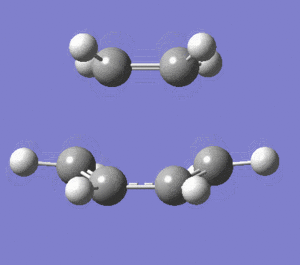 |
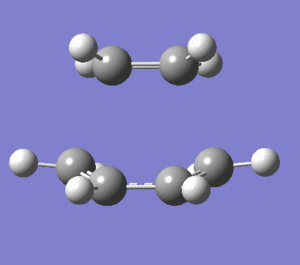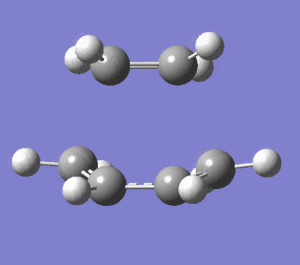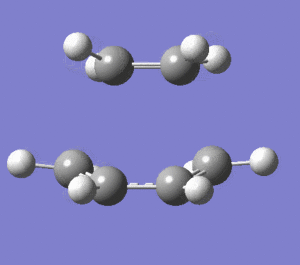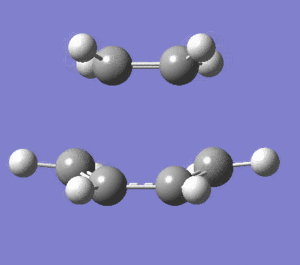 |
The vibration that corresponds to the reaction path is synchronous and symmetric. The terminal carbons of both fragments have the largest vibrations and they all come closer and move away in a concerted motion. The vibrations of the terminal carbons correspond to the bond formation and breakage between the two fragments. This vibrational mode is a combination of stretching and bending of the bonds. The forming bonds between the terminal carbons are stretch but both of them are stretched synchronously. The lowest positive frequency vibrates in much smaller amplitudes. This is bending mode and has smaller frequency value compared to the imaginary frequency(bending modes are lower frequency than stretching modes). The way the atoms bend in this mode doesn't correspond to the bond formation between the terminal carbons because they move very little towards each other. This bending mode is also not symmetric.
The IRC analysis was also carried out for this reaction. The reaction coordinate was computed both ways(not symmetric path) with 100 points along the IRC bath. The HF/3-21G level of theory was used(DOI:10042/26756 ).
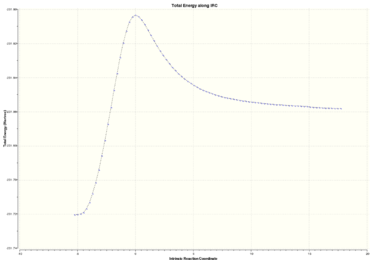 |
 |
As can be seen above, the the IRC path is not symmetric. The reactants ethylene and butadiene represent the right side of the IRC path whereas the product cyclohexene represents the left hand side. The product molecule is more stable than the reactants which is expected for a favourable reaction. The IRC path goes via the TS which the highest energy point. This reaction coordinate path is characteristic for pericyclic reactions because it doesn't involve any intermediates. The reaction between the molecules can be viewed on right. The animation shows how the bonds are synchronously formed between the two species. The bonds of cis-butadiene molecule twists slightly in the end. The molecule should in theory be planar(delocalisation of p orbitals) but the structure could be affected by the method which is used for analysis, in this case, the HF method.
Molecular Orbitals of Butadiene and Ethylene Cycloaddition Reaction
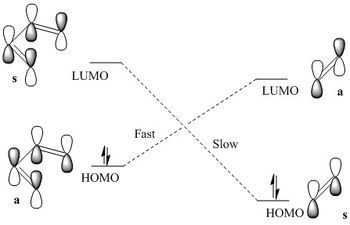
The HOMO and LUMO interactions are crucial in determining the outcome of the cycloaddition reactions. This is also the case for the Diels-Alder reaction between butadiene and ethylene(dienophile). The molecular orbitals at the transition state are formed by the interactions of HOMO and LUMO of both of these species. For the reaction to be allowed the HOMO of one reactant has to interact with the LUMO of the other reactant. This can only happen when the interacting orbitals have the right symmetry because then the orbitals can overlap constructively. If the symmetry of orbitals is different then the reaction is forbidden. For this reaction there are two possible HOMO-LUMO interactions which are symmetry allowed-HOMO(butadiene) with LUMO(ethylene) or HOMO(ethylene) with LUMO(butadiene). The HOMO-LUMO gap of butadiene is smaller than the HOMO-LUMO energy gap of ethylene due to the delocalisation of p-orbitals. As can be seen in the diagram on right, the HOMO(butadiene)-LUMO(ethylene) gap is smaller compared to HOMO(ethylene)-LUMO(butadiene) energy gap. This means that smaller energy is needed for the HOMO(diene)-LUMO(ethylene) interaction and therefore the Ea is also smaller which gives faster reaction via these orbital interactions.[4]
To test the theory, the HOMO and LUMO of the TS were also plotted using the check point file from the AM1 semi-empirical optimisation (AM1 good for organic molecules). The prediction is that the HOMO of TS should resemble the orbitals of HOMO(butadiene)-LUMO(ethylene) pair.
The HOMO and LUMO are given below:

The HOMO of the TS is antisymmetric with respect to the reflection plane(plane is vertically perpendicular to the screen and goes through the centres of both molecules). It is antisymmetric because the lobes of orbitals change phases(signs) with respect to the reflection plane. An interesting feature of this HOMO was observed because the bottom lobes on each side of the ethylene molecule have different sizes. This could possibly be due to the fact that bond lengths between the fragments were not completely equal(they were the same until 2 decimal places) therefore the contribution from ethylene orbitals towards the HOMO of the TS may not be equal. In addition, this could also mean that this cycloaddition reaction is not completely concerted which could in theory occur. The LUMO is symmetric with respect to the reflection plane because the signs of the orbitals on both sides of the plane are the same.
So the HOMO of the TS is antisymmetric. The HOMO of butadiene and LUMO of ethylene have formed this HOMO of the TS. This is allowed reaction because the HOMO of butadiene is antisymmetric and also the LUMO of ethylene is antisymmetric. As the interacting orbitals of reactants have the right symmetry to interact, the overlap of these orbitals is good hence the reactions can occur. The LUMO of the TS is symmetric but is not allowed reaction because the interacting lobes of the terminal carbons don't have the right symmetry to interact and hence have no good constructive overlap. There is however some weak constructive orbital overlap between the ethylene orbitals and the orbitals from the two central carbons of butadiene. Important to note that the lobes in the TS are formed by the overlap of C p orbitals.
The HOMO of butadiene/ethylene TS from DFT/B3LYP/6-31G(D) calculations is shown on the right. As can be seen this HOMO is different from the HOMO obtained by the AM1 method. This HOMO orbital doesn't resemble any of the HOMO-LUMO interactions mentioned above because it looks like the terminal carbons of butadiene don't contribute their p-orbitals towards this HOMO. There are no nodes at the centers of these carbons. This shows that different methods could interpret the wavefunctions differently which is why different HOMO orbitals were obtained for AM1 and DFT methods. It was discovered that the MO, which is HOMO in AM1, is HOMO-1 in DFT; and the MO ,which is HOMO in DFT,is HOMO-1 in AM1.
The Regioselectivity of the Diels Alder Reaction
In this part, the Diels Alder reaction between cyclohexa-1,3-diene and maleic anyhydride was investigated. The reaction between these species can give two possible products-exo and endo. The endo product should be the dominant product because the reaction is supposed to be kinetically controlled. The exo and endo transition states were also computed in order to calculate the activation energies and to get the reaction path.
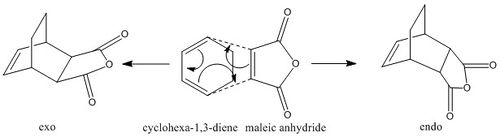
Optimisation of the Endo and Exo Transition States
In order to locate the transition state structure, the guess structure was needed. The first guess for the distance between the interacting carbon atoms was about 2.50 Å but this distance was too far from the real structure and the forces and displacements in optimisation couldn't converge. Then the distance was decreased to about 2.00 Å and it turned out to be the right one. The optimisation was carried out using the frozen coordinate method(with Opt=NoEigen keywords). At first, the guess TS was optimised using AM1 semi-empirical level of theory(the reactants were optimised to minimum before the TS guess structure was located).
 |
 |
 |
 |
Both of the optimised TS structures had one imaginary frequency which vibrations resembled the bond formation between the two molecules hence the TS corresponding to the reaction path was found. The table below shows the bond lengths and imaginary frequnecies of both transition states:
| TS | Length of the partly formed σ bond (Å) | Imaginary frequency (cm-1) |
| Exo | 2.17 | -812 |
| Endo | 2.16 | -807 |
The lengths of the partly formed bonds are nearly the same and that is also reflected in the frequencies which are very similar. The transition states were further optimised by HF/3-21G(LOG exo;LOG endo) and DFT/B3LYP/6-31G(d)(LOG exo;LOG endo) levels of theory. The table which summarises the results from HF/3-21G optimisation is given below:
| TS | Length of the partly formed σ bond (Å) | Imaginary frequency (cm-1) |
| Exo | 2.26 | -648 |
| Endo | 2.23 | -644 |
The partly formed bond distances are again very similar but slightly longer compared to the distances optimised by AM1 method. One imaginary frequency was found for each TS. Lower vibrational frequency of the HF bonds compared to the AM1 bonds mirrors the increase of the bond lengths.
The resulting TS structures were very similar in shape for the HF and DFT levels of theory. To illustrate the outcome of calculations, the DFT/B3LYP/6-31G(d) optimised structures are shown below:
| Exo TS structure | Exo TS model | Endo TS structure | Endo TS model | ||||||
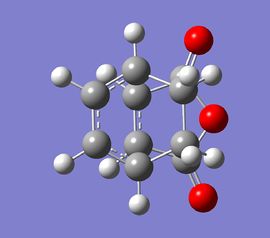 |
|
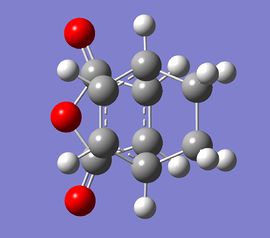 |
|
As can be seen in the images above, the relative orientation between the two molecules is different for the exo and endo structures. This orientation then determines whether the exo or endo product is made in the reaction. However, there are several factors which affect the relative orientation of these molecules and hence the regioselectivity of the reaction. The outcome of the reaction is mainly affected by the competition between the sterics and stereoelectronics of the exo and endo forms.
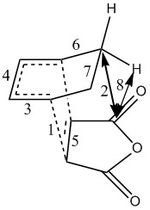
The steric interactions can be analysed by looking at distances between the relevant atoms. Some important bond lengths and interaction distances are displayed below:
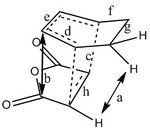
| Bonds/interactions | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | a | b | c | d | e | f | g | h |
| Distances(Å) | 2.29 | 3.03 | 1.39 | 1.40 | 1.40 | 1.51 | 1.56 | 2.53 | 2.35 | 2.99 | 2.27 | 1.39 | 1.40 | 1.52 | 1.56 | 1.39 |
The exo and endo TS structures with the important bond lengths and interactions are shown on right. The lengths of the partly formed bonds are very similar for both transition state structures and they are 2.29 and 2.27 Å for exo and endo transition states respectively. This means that these bonding interactions which lead to the formation of the sigma bonds could potentially be very similar strength. Of course, a lot of in this case would also depend on the orbitals involved in these interactions. The distance of these interactions are longer than single/double bonds and shorter than the sum of two carbon atom van der Waals radii which means that the orbitals of the interacting atoms can overlap. The bonds 3,4,6,7 and d,e,f,g are bonds from the cyclohexa-1,3-diene fragment. All the corresponding bond lengths of both cyclohexa-1,3-diene molecules are the same length, except for the f/6 pair where f is 0.01 Å longer. Overall, this means that bond lengths and shape of cylohexa-1,3-diene fragment of both transition states are nearly identical. The bonds h and 5 of maleic anhydride fragments have nearly equal length. Bonds 7 and g are longer than bonds 6 and f because these bonds experience more strain due to the forming bridge. Important to note that the bonds which are represented as single bonds plus the dashed lines have partial double bond character. These bonds are longer than normal double bonds (1.34 Å) but also shorter than regular single bonds (1.54 Å ). The bonds and interactions mentioned above have very similar lengths but there should be interactions which would favour one mode over the other mode in the reaction. Few such interactions can be identified for both structures.
Two types of through space interactions, which could possibly affect the reactivity, can be found for the exo TS structure. Those are interactions 2 and 8. The length of interaction 2 is 3.03 Å which is longer than normal C-C single and double but it is shorter than sum of two C van der Waals radii (3.4 Å) . The fact that this distance is shorter than the sum of van der Waals radii could suggest that the C atoms are slightly repulsive (or very slightly attractive). The length of these interactions can be very important when considering molecular orbitals and how they interact. The length of interaction 8 is 2.53 Å. It is between the H atom and C atom(from-C=O). This distance between the interacting atoms is smaller compared to the previous interaction distance. However, this interaction could be described more as an electrostatic interaction, more specifically as electrostatic repulsion. This is because the H atom in C-H bond carries a partial positive charge(C more electronegative than H) and C in C=O bond also carries a positive charge, and they both repel each other. There are no H bond type interactions because the distances between hydrogens and oxygens are too long.
The endo structure also has two types of interactions. First important interaction is interaction b which is 2.99 Å long and is between two C atoms (C(H) and C(=O)) . This distance is again longer than normal C-C bond distances but is shorter than the sum of two van der Waals radii. This interaction is possibly slightly repulsive and leads to destabilisation of the TS. There is another interaction labelled as a. It is 2.35 Å long and is very close the the sum of van der Waals radii of two hydrogens (2.20 Å) . This means that this interaction is not repulsive because the the distance is larger than the sum of van der Waals radii. This interaction is most probably attractive interaction between two H atoms (There are also weak van der Waals interactions between hydrogens but these interactions are present in both transition states).
So the stability of both transition states depends on how strong the interactions 2/8 and a/b are. The interaction b in the endo TS is more repulsive (destabilising) than interaction 2 in the exo form because the length of the interaction b is shorter than the length of interaction 2. Interaction 8 in the exo TS is repulsive but interaction a in the endo TS is attractive. It is difficult to determine which transition state is affected the most by sterics without calculations but the electrostatic repulsion in the exo TS may disfavour this TS structure.
Examination of the HOMOs
 |
 |
 |
 |
The HOMO orbitals of the exo and endo transition states are shown above(each with two different views). It is known that endo product is mainly formed because of so called secondary orbital interactions. Originally Woodward and Hoffman postulated that endo stereoselectivity results from favourable secondary orbital interactions between the diene and dienophile which do not become bonded in the adduct.[5] This means there should be more such interactions in the endo TS compared to the exo TS.
Some secondary orbital interactions are observed in the exo TS. There could be possible through space interactions between the orbitals of the -C(O)-O-C(O)- fragement and the orbitals of opposite -CH2-CH2- group(View 1). More specifically the interactions are between the oxygen (from C=O) p orbitals and carbon(from -CH2-CH2- group) outward leaning p type orbitals(p-orbitals because there is a node at the centre of the corresponding atom). The C and O orbitals interact constructively because the phases of interacting orbitals match. However, these interactions are probably weak/medium through space interactions. Important to note that C p orbitals are not linear; they are slightly bent towards the oxygen p orbitals in this way maximising the interactions. There is also a very noticeable nodal plane going through the centres of the two molecules(vertical plane which is perpendicular to the central O atom from C(O)-O-C(O) group). The HOMO is antisymmetric with respect to this plane. In view 2 it can be seen how the p type orbitals overlap constructively. This is a strong bonding interaction because the p type orbitals have the right phase and orientation to overlap significantly and hence form σ bonds.

In the image view 1 of the endo HOMO it can be seen that there are strong p σ type interactions between the p π type orbitals of both molecules. The p type orbitals of each molecule have the right orientation to overlap strongly in order to form σ bonds. In the view 1 it can also be seen that the bottom lobes of C p type orbitals from the CH2-CH2 fragment have the right phase to interact with the bottom lobes of C p type orbitals from the C(H)=C(H) fragment(maleic anhydride). These interactions are probably very weak through space interactions but they still could increase the overall stability of the endo TS. In view 2 of the endo TS one attractive interaction is observed. In this case the interaction is between the O p orbital(from C(O)-O-C(O) fragment) and C p π type orbitals of the opposite -C(H)-C(H)- group. This secondary orbital interaction is most probably very weak because the interacting orbitals are very dissimilar in size and they are far apart. The orbitals are also not directed towards each other very well. The O p orbitals are orthogonal to C p type orbitals. This HOMO is antisymmetric with respect to the nodal plane which goes through the centre of the molecules(similarly to the exo HOMO).
The relative stability of these HOMOs will depend on the strength of the overall constructive secondary orbital interactions because the orbital interactions which give σ bonds are very similar. So far it seems that the secondary interactions in both structures could be roughly similar. The interaction in the exo HOMO between the O p and C p orbitals is probably stronger than interaction between the O p and C p orbitals in the endo HOMO for the reasons discussed above. There is one additional constructuve interaction in the endo HOMO but it is probably very weak interaction. So the overall stability of HOMO for both molecules could be very similar. But why then it is known that endo TS is favoured significantly by the secondary orbital interactions? The endo HOMO -1 is given on the right. As can be seen in the image, there is a good secondary orbital interaction between the O p orbitals(from C(=O)-C-C(=O) fragment) and the C p π type orbitals from the opposite C(H)-C(H) fragment. These interactions are constructive because the interacting orbitals have the right phases to interact. This interaction is very similar to the interaction already mentioned for the exo HOMO. However, there are no good secondary orbital interactions in the exo HOMO -1. This means that overall the endo TS is more stabilised by the secondary orbital interactions compare to the exo TS. The HOMO -1 also contributes to the overall stability of the TS because the molecular orbitals are spread all over(delocalised) the structure and they have to be considered together. The HOMO and HOMO -1 orbitals are also very close in energy.
The Relative Energies of Exo and Endo Transition States
In order to calculate the relative energies of the exo and endo transition states, the energy of reactant molecules is needed. The maleic anhydride and cyclohexa-1,3-diene molecules were optimised separately using HF/3-21G and DFT/B3LYP/6-31G(d) levels of theory(LOG files: HF and DFT LOG maleic anhydride, HF and DFT LOG cyclohexa-1,3-diene). The energies of the reactants and transition states are summarised in the table below.
| HF/3-21G (Hartrees) | B3LYP/6-31G(d) (Hartrees) | |||||
|---|---|---|---|---|---|---|
| Electronic energy | Sum of electronic and zero-point energies | Sum of electronic and thermal energies | Electronic energy | Sum of electronic and zero-point energies | Sum of electronic and thermal energies | |
| at 0 K | at 298.15 K | at 0 K | at 298.15 K | |||
| Exo TS | -605.603591 | -605.408139 | -605.398678 | -612.679311 | -612.498013 | -612.487663 |
| Endo TS | -605.610368 | -605.414902 | -605.405476 | -612.683396 | -612.502143 | -612.491790 |
| Cyclohexa-1,3-diene | -230.539671 | -230.407721 | -230.403455 | -233.415885 | -233.293216 | -233.288621 |
| Maleic anhydride | -375.103514 | -375.042900 | -375.038067 | -379.289545 | -379.233657 | -379.228473 |
| Reactants | -605.643185 | -605.450621 | -605.441522 | -612.705430 | -612.526873 | -612.517094 |
In order to calculate the relative energy of exo and endo transition states, the total energy of reactants was subtracted from the energy of the TS. The energy units were then converted from Hartrees to kcal/mol (1 Hartree = 627.509 kcal/mol ). The results are shown in the table.
| TS | ΔEa HF/3-21G at 0K (kcal/mol) | ΔEa HF/3-21G at 298.15 K (kcal/mol) | ΔEa B3LYP/6-31G(d) at 0 K (kcal/mol) | ΔEa B3LYP/6-31G(d) at 298.15 K (kcal/mol) |
|---|---|---|---|---|
| Exo TS | 26.66 | 26.88 | 18.11 | 18.47 |
| Endo TS | 22.41 | 22.62 | 15.52 | 15.88 |
The ΔE values were obtained for two different temperatures - 0 and 298.15 K. As can be seen the ΔE values are slightly larger at 298.15 K than they are at 0 K. The ΔE values obtained by DFT method are smaller compared to the values obtained by the HF method. The main observation is that ΔE values via the endo transition state are smaller than the ΔE values via the exo transition state. This agrees with the theory which states that endo product is the kinetic product hence has smaller ΔE.[6]
The stability of the exo and endo transition states was discussed in the previous parts. It was shown that sterics and electronics slightly favour the the endo TS which agrees with the theory and is also reflected in the calculated ΔE values.
IRC analysis of the Diels Alder reaction
The Intrinsic Reaction Coordintate method was used to compute the reaction path via the endo and exo transition states(the exo DOI:10042/26757 ;the endo DOI:10042/26758 ). The reaction coordinate was calculated in both directions(100 steps) as the reaction path for this reaction is not symmetric. The DFT/B3LYP/6-31G(d) level of theory was used.
The IRC path via the exo transition state is shown below. The animation which shows how the reaction proceeds is also shown(for some reason it can only be seen when it is clicked).
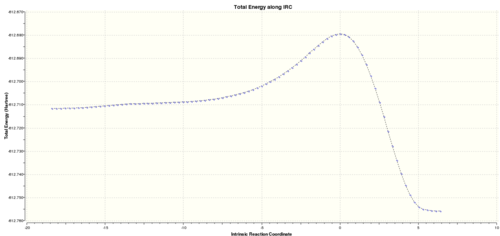 |
 |
The reaction coordinate is not symmetric because the reactants combine to give the exo product which is lower in energy. So this reaction is thermodynamically driven reaction. The highest energy point on the path is the exo TS. This type of reaction coordinate is typical for pericylic reactions which proceed concertedly via the TS and involve no intermediates. The reaction coordinate via the endo transition state is also given.
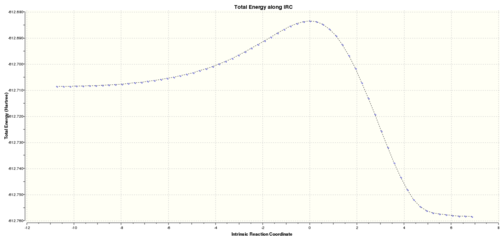 |
 |
The reaction coordinate via the endo TS is very similar to the exo one. The path goes via the TS and involves no intermediates. The energy of the endo product is lower than the energy of reactants-maleic anhydride and cyclohexa-1,3-diene.
The endo and exo products are shown below(from IRC analysis):
 |
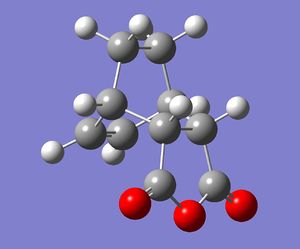 |
Structurally the product molecules look as they were expected to be. The -C(O)-O-C(O)- group is syn to the -C(H)=C(H)- group in the endo product but -C(O)-O-C(O)- group is anti to -C(H)=C(H)- group in the exo product. Although it is known that exo product is the thermodynamic product, the calculated energy of exo product is higher compared to the endo product. Many studies have been carried out to investigate the the exo and endo selectivity of the Diels Alder reactions and the studies of many reactions have shown that the exo product is the thermodynamic product.[7] The total electronic energies of the exo and endo products (energies taken from output of DFT/B3LYP/6-31G(d) IRC analysis) are -612.755754 and -612.758292 Hartrees respectively. The energgy difference between the two products in this case is 1.59 kcal/mol. The product molecules were also optimised using HF/3-21G method(LOG exo. LOG endo). The energies of the exo and endo products in this case were found to be -605.718735 and -605.721320 Hartrees respectively. The energy difference between the HF products is 1.62 kcal/mol, so it is higher compared to the energy difference between the DFT optimised products. The DFT/B3LYP/6-31G(d) is higher level of theory compared to the HF/3-21G method and smaller energy difference between the products was obtained by the DFT method. So there could be a possible correlation between the level of theory used and the energy difference of products. the DFT and HF methods are not the best possible computational methods. It is possible that more advanced computational methods would lower the energy gap even more and maybe give the exo product as the thermodynamic product. There are also error associated with the calculated energy which is about 2.39 kcal/mol(value obtained from Dr. T. Hunt's 'Computational Chemistry Lab' website). This error is larger than the energy difference between the products so the exo product could possibly be lower in energy than the endo one, if the error is considered.
The ΔE values for the transition states were obtained from the sum of electronic and zero-point energies, and the sum of electronic and thermal energies. In general the relative energies and activation energies are obtained from the free energies (G). Free energy is a thermodynamic quantity which also includes the contributions from the enthalpy and entropy. All of these quantities have been neglected in these calculations because the electronic and thermal energies were used instead. The computational method we were using is based on quantum mechanics but approximations have to be made in order to calculate the properties of any system. One approximation that is used in calculations is Born-Oppenheimer approximation which states that electron and nuclear motions can be separated because nuclei are much heavier than electrons and hence the nuclei can be assumed to be stationary. The approximations also vary between the methods. For example, one determinant is only used in HF method to calculate the molecular wavefunctions. In HF method each electron only sees the average repulsion of the remaining electrons. Another example is the the DFT method which uses LCAO approximation. All of these assumptions affect the outcome of calculations which could possibly give results which do not agree with the experimental results.
References
- ↑ B. G. Rocque, J. M. Gonzales, and H. F. Schaefer III, "An analysis of the conformers of 1,5-hexadiene", Mol. Phys., 2002, 100, 441-446.DOI:10.1080/00268970110081412
- ↑ G. Schultz, I. Hargittai, "Conformational investigation of gaseous 1,5-hexadiene by electron diffraction and molecular mechanics", J. Mol. Struct., 1995, 346, 63-69.DOI:10.1016/0022-2860(94)09007-C
- ↑ M. Mantina, A. C. Chamberlin, R. Valero, C. J. Cramer, and D. G. Truhlar, "Consistent van der Waals Radii for the Whole Main Group", J. Phys. Chem., 2009, 113, 5806-5812.DOI:10.1021/jp8111556
- ↑ X. Sun, Organic Mechanisms: Reactions, Methodology, and Biological Applications, Wiley, 2013, 131-132.
- ↑ R. B. Woodward, R. Hoffmann, The Conservation of Orbital Symmetry, Verlag Chemie: Weinheim, 1971.
- ↑ I. Fleming, Molecular Orbitals and Organic Chemical Reactions, Wiley, 2009, 235-238.
- ↑ M. A. Fox, R. Cardona, and N. J. Kiwiet, "Steric effects vs. secondary orbital overlap in Diels-Alder reactions. MNDO and AM1 studies", J. Org. Chem., 1987,52, 1469–1474.DOI:10.1021/jo00384a016