Rep:Mod:kk5217year1mod2
NH3 Molecule
| Molecular Formula | Calculation Method | Basis Set | Final Energy (au) | RMS Gradient (au) | Point Group | Bond Length (Å) | Bond Angle (°) |
|---|---|---|---|---|---|---|---|
| NH3 | RB3LYP | 6-31G(d,p) | -56.55776873 | 0.00000485 | CV3 | 1.01798 | 105.741 |
Item Value Threshold Converged?
Maximum Force 0.000004 0.000450 YES
RMS Force 0.000004 0.000300 YES
Maximum Displacement 0.000072 0.001800 YES
RMS Displacement 0.000035 0.001200 YES
Predicted change in Energy=-5.986277D-10
Optimization completed.
-- Stationary point found.
----------------------------
! Optimized Parameters !
! (Angstroms and Degrees) !
-------------------------- --------------------------
! Name Definition Value Derivative Info. !
--------------------------------------------------------------------------------
! R1 R(1,2) 1.018 -DE/DX = 0.0 !
! R2 R(1,3) 1.018 -DE/DX = 0.0 !
! R3 R(1,4) 1.018 -DE/DX = 0.0 !
! A1 A(2,1,3) 105.7412 -DE/DX = 0.0 !
! A2 A(2,1,4) 105.7412 -DE/DX = 0.0 !
! A3 A(3,1,4) 105.7412 -DE/DX = 0.0 !
! D1 D(2,1,4,3) -111.8571 -DE/DX = 0.0 !
--------------------------------------------------------------------------------
Jmol file
NH3 molecule |
Display Vibrations
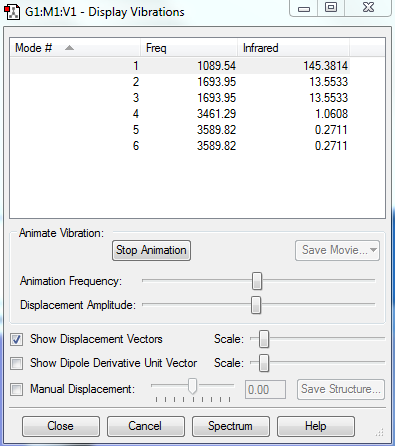
6 vibrational modes are expected from the 3N-6 rule. (N=4, hence 12-6=6). From the data above, the modes number 2 and 3 are degenerate, while the modes 5 and 6 are also degenerate. From the animation, the first three modes are bending modes (lower frequency), while the last 3 are stretching modes (higher frequency). Mode 4 is highly symmetric, as it is the symmetrical stretch of the H atoms. The umbrella mode is the bending mode associated with mode 1, where the H atoms move symmetrically from the N atom upwards and downwards. Since there are 2 pairs of degenerate vibrations, 4 (6-2=4) bands would be expected in the infrared spectra.
Charges on each atom
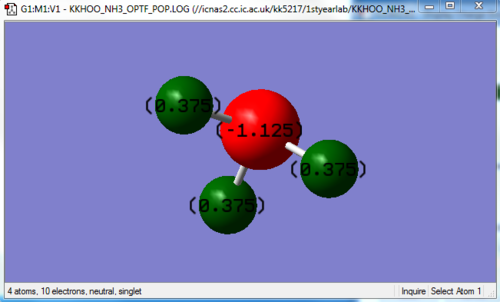
Because nitrogen is more electronegative than hydrogen, a negative charge is expected on the N, since it is known to pull electron density away from the hydrogens and to itself. This is observed in the image above, showing the calculated charges on the N and H are -1.125 and 0.375 respectively. Also note how they add up to 0, showing the molecule has no overall charge.
The optimisation file for NH3 is here
The Haber-Bosch Process
| Molecular Formula | Calculation Method | Basis Set | Final Energy (au) | RMS Gradient (au) | Point Group | Bond Length (Å) | Bond Angle (°) |
|---|---|---|---|---|---|---|---|
| NH3 | RB3LYP | 6-31G(d,p) | -56.55776873 | 0.00000485 | CV3 | 1.01798 | 105.741 |
| N2 | RB3LYP | 6-31G(d,p) | -109.52412868 | 0.00000060 | D*H | 1.10550 | N/A |
| H2 | RB3LYP | 6-31G(d,p) | -1.17853936 | 0.00000017 | D*H | 0.74279 | N/A |
Data
The data in the table above was taken from GaussView. The data for the H2 and N2 is shown below, in similar fashion to the above data for NH3
H2 molecule
Item Value Threshold Converged?
Maximum Force 0.000000 0.000450 YES
RMS Force 0.000000 0.000300 YES
Maximum Displacement 0.000000 0.001800 YES
RMS Displacement 0.000001 0.001200 YES
Predicted change in Energy=-1.164080D-13
Optimization completed.
-- Stationary point found.
----------------------------
! Optimized Parameters !
! (Angstroms and Degrees) !
-------------------------- --------------------------
! Name Definition Value Derivative Info. !
--------------------------------------------------------------------------------
! R1 R(1,2) 0.7428 -DE/DX = 0.0 !
--------------------------------------------------------------------------------
H2 molecule |
The optimisation file for H2 is linked here
N2 molecule
Item Value Threshold Converged?
Maximum Force 0.000001 0.000450 YES
RMS Force 0.000001 0.000300 YES
Maximum Displacement 0.000000 0.001800 YES
RMS Displacement 0.000000 0.001200 YES
Predicted change in Energy=-3.401063D-13
Optimization completed.
-- Stationary point found.
----------------------------
! Optimized Parameters !
! (Angstroms and Degrees) !
-------------------------- --------------------------
! Name Definition Value Derivative Info. !
--------------------------------------------------------------------------------
! R1 R(1,2) 1.1055 -DE/DX = 0.0 !
--------------------------------------------------------------------------------
N2 molecule |
The optimisation file for N2 is linked here
From this table:
E(NH3) = -56.55776873
2*E(NH3) = -113.11553746
E(N2) = -109.52412868
E(H2) = -1.17853936
3*E(H2) = -3.53562808
ΔE=2*E(NH3)-[E(N2)+3*E(H2)]= -113.11553746+109.52412868+3.53562808 = -0.0557907 au
-0.0557907 au * 2625.5 = -146.47848285 kJmol-1
From this, we can see that ammonia is more thermodynamically stable; the energy is lower than that of it's elements in their standard state.
Independent Investigation: Hydroxide Ion [OH]-
The hydroxide ion was analyzed in the same way as the molecules above. The link to the optimisation file is shown here.
OH- |
The molecule under investigation is [OH]-, which has 2 atoms: an oxygen and a hydrogen, with 10 electrons shared between them, where the total number of protons between them is 8+1=9, leaving an overall -1 negative charge.

Similarly to the N in NH3, the O in [OH]- is much more electronegative than the H. We therefore expect it to draw electron density towards itself and away from the H atom, leaving an overall negative charge on the oxygen atom, and a positive charge on the hydrogen. This can be seen in the image above - note how the charge adds up to -1, indicating an overall -1 charge on this molecule.
| Molecular Formula | Calculation Method | Basis Set | Final Energy (au) | RMS Gradient (au) | Point Group | Bond Length (Å) | Bond Angle (°) |
|---|---|---|---|---|---|---|---|
| NH3 | RB3LYP | 6-31G(d,p) | -75.72629185 | 0.00000199 | C*V | 0.98339 | N/A |
This is the optimisation data shown in the table - however, we can compare this to the literature bond length of the hydroxide anion. In solution, OH- will be surrounded by water molecules, each coming close enough to the negative O atom to form hydrogen bonds; this results in a species that sometimes exists in a more stable state of the hydrogen bonded H3O2-. In this species, the bond length for the O-H is 0.733 Å[1]. However, this is in a crystal structure. By comparison, the O-H bond length in H2O (water) is 0.95718 Å[2]. This is similar to the calculated optimised 0.98339 Å from GaussView. Differences could arise in reality due to hydrogen bonding, which could result in a broad range of slightly fluctuating bond lengths, and the additional proton in H2O.
The HOMO of the OH- anion

This image shows the highest occupied molecular orbital of the OH- anion. However, as seen in the table on the side of the image, there are two orbitals that are degenerate and are orthogonal to each other in the same plane (one phase above and one phase below the axis of the molecule). These are the 2p orbitals (2px and 2py).
The LUMO of the OH- anion
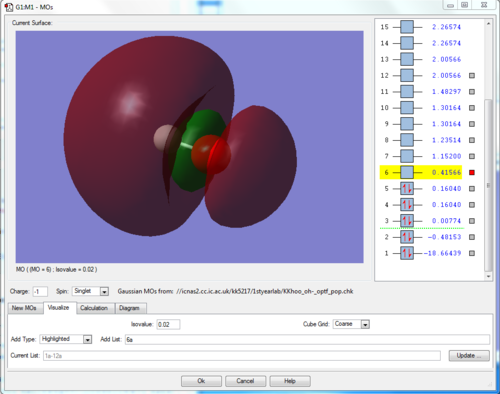
Here we see the lowest unoccupied molecular orbital of the OH- anion. It is an antibonding (σ *) orbital arising from the combination of the hydrogen's 1s orbital with the one of the oxygen's 2p orbitals (2pz). The clear s and p characters of the H and O show respectively, however note that since this is the antibonding orbital and is closer in energy to the 1s orbital of the H, the shape of the orbital is also more towards the H side. On the other hand, the bonding orbital of the linear combination of these orbitals is shown below - this is the σ orbital.
The bonding σ orbital

In this bonding orbital, the 2pz character is quite clearly seen, with the opposite phases shown in green and red, and a greater pull of electron density towards the oxygen atom.
The 2s orbital
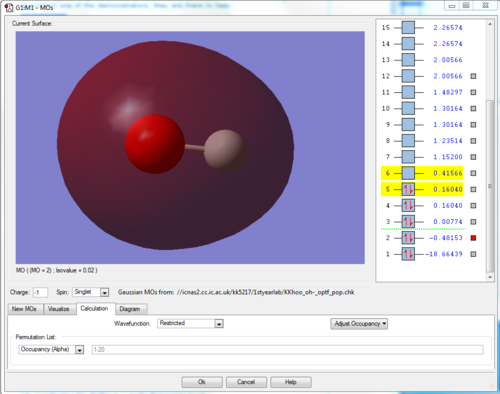
This orbital, shown above, is degenerate in energy to the original 2s orbital of the oxygen atom - due to a lack of interaction between this orbital and the orbital(s) of the hydrogen atom, it remains the same in energy.
The 1s orbital
Similarly to the 2s orbital above, the 1s is even more tightly bound to the O, since it is an entire n level lower. It therefore hardly interacts with the H nucleus and is centered completely around the O.
References
- ↑ D. T. Puerta and S. M. Cohen, [(TpMe,Ph)2 Zn2(H3O2 )]ClO4 : a new H3O2 species relevant to zinc proteinases, Inorganica Chimica Acta, 337 (2002) 459-462..
- ↑ J. B. Hasted, Liquid water: Dielectric properties, in Water A comprehensive treatise, Vol 1, Ed. F. Franks (Plenum Press, New York, 1972) pp. 255-309.
