Rep:Mod:kk3015TS

Introduction

Potential Energy Surface (PES)

Fig. 1: PES of a water molecule, illustrating the minima at the equilibrium O-H bond lengths and H-O-H bond angles.

A potential energy surface (PES) outlines the potential energy (V) of a system with respect to certain parameters, usually its geometrical configuration, meaning that a molecule's potential energy is dependent on the internal coordinates (x) of each atoms. This dependency of the PES with the molecular geometry means that the PES will have the same dimensionality as the molecule's degree of freedom (3N-6 for a non-linear molecule, where N is the number of atoms in the molecule). A minimum point on the PES will therefore correspond to the molecular geometry with the lowest energy, which translates mathematically to $(\frac{\partial V}{\partial x}=0)$ and $(\frac{{\partial }^{2}V}{\partial x^{{}^2}}>0)$. The first derivative being zero simply means that it is a stationary point, not specifically a minima; an example of this is shown in fig. 1. While the first derivative corresponds to the force acting on the molecule (zero at the minima), the second derivative can be equated to the force constant, k, which is positive in all directions since $(k=\frac{{\partial }^{2}V}{\partial x^{{}^2}}>0)$. The dependency of the vibrational magnitude to the bond strength, $(v\sim \sqrt{k})$, means that if the force constant (k) is positive in all directions, then the wavenumber ("v") will also be positive for all the vibrational states of the molecule in the minima configuration.

Fig. 2: A general PES shown with two minima (A and B), which could be the reactant, product, or conformers, with a saddle point in the middle.

On the other hand, a "saddle point", which can be seen as a maxima between two minima (fig. 2), corresponds to a transition state. On the PES, this point is mathematically defined to have a second derivative that is positive in all directions (a minima) but one direction, where its second derivative is positive (a maxima). In the chemical sense, going from reactant to product, the system requires sufficient energy to overcome the transition state energy barrier (the activation energy), which is the highest point on the reaction coordinate. Using the same justification as before, where the force constant (k) equates to the second derivative of the PES plot, the transition state and saddle point is expected to have a single negative (imaginary) vibrational frequency due to its second derivative being positive (maxima) in one direction, $(k=\frac{{\partial }^{2}V}{\partial x^{{}^2}}<0)$.

Nf710 (talk) 23:16, 5 March 2018 (UTC) This is correct but you can get this info from diagonalizing the Hessian. Where the eigenvalues are the force constants and the eigenvectors are the normal modes

Calculation and Computational methods

Using Gaussian to determine the transition state structure, three different calculation methods were employed. The first (and fastest) method requires some knowledge of the mechanistic approach of the reaction in order to guess the possible structure of the transition state, which is then optimised. Although this method is the fastest of the three, it is also rather unreliable as there is a likely chance that the transition state will be guessed incorrectly.

The second method involves "freezing" the reacting termini of the previously optimised reactants at a distance somewhere between that of the reactant and product, before optimising it to the minima, followed by the transition state calculation. Due to the fact that the atoms involved in bond formation are frozen, there is a higher chance of success compared to the first method as we are applying additional insight of the transition state.

The last method is the most time-consuming due to involving more steps than the other two, but it is also the most reliable. It starts with either optimising the reactants or the product to the minima; if the reactants are first optimised, their configurations will be arranged similarly to that of the transition state, before the reacting termini are frozen, and the rest of method 2 are repeated. On the other hand, starting by optimising the product would mean that the new bonds formed would need to be broken and separated at a distance somewhere between that of the reactant and product, before the reacting termini are frozen once again, and the structure is optimised to a transition state. Calculations carried out in the last two exercises used the third method due to its reliability, while the first exercise was done with the second method as a compromise between time and reliability.

Using the computer program Gaussian, two calculation methods were employed to process and optimise the reactions. Gaussian uses a quantum mechanic foundation for estimating the energy of the molecular orbitals (MOs) through the use of Linear Combination of Atomic Orbitals (LCAO). Relying also on the Born-Oppenheimer approximation when establishing the PES plot, Gaussian solves the time-independent Schrödinger equation ($E=<\mathrm{\Psi }|H|\mathrm{\Psi }>$) to estimate the energy (E) and the wavefunction (Ψ).

The first method used was the semi-empirical PM6 method (based on the Hartree-Fock approach), which makes experimental data-based approximations in order to solve the Schrödinger equation. Optimisation with this method is done relatively quickly, but is also fairly unreliable at times if the environment of the molecule under calculation is too different from the approximated conditions.

In comparison, the hybrid B3LYP method, which uses the Density Functional Theory (DFT), carries out calculations that are more reliable but also more time-consuming. This method still uses the Hartree-Fock approach to calculate the exchange-correlation term, while the rest of the Hamiltonian expression are calculated individually with DFT. The 6-31G basis set was used by B3LYP calculations to represent the electronic wavefunction, giving a more precise and accurate calculation at the cost of significantly longer processing time.

Nf710 (talk) 23:16, 5 March 2018 (UTC) Good understanding of the methods. You coudl have shown sown understanding of basis sets and possibly some equations

Exercise 1: Reaction of Butadiene with Ethylene

(Fv611 (talk) Good job on this whole exercise. Well done!)

Fig. 3: [4+2] Cycloaddition between butadiene and ethylene

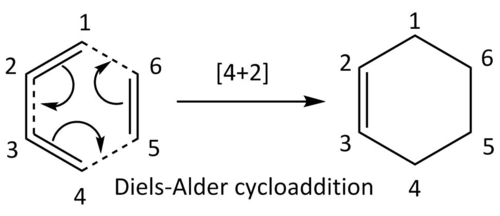
Using the basis of the second method outlined in the introduction, this exercise explores the [4+2] (Diels-Alder) cycloaddtion between 1,3-butadiene (acting as the diene), and ethylene (acting as the dienophile). Starting off by minimising the two reactants, these two structures were put together before being optimised to a transition state. The obtained transition state was confirmed to be fully converged, and the vibrational results were also reasonable. An IRC of this was then calculated, as illustrated below, before the structure of the final product was constructed and minimised. All of the calculations mentioned were done at the PM6 level.

As previously specified, the pericyclic reaction is a thermal [4+2] Diels-Alder cycloaddition, counting on the 4π electrons on the diene interacting with the 2π electrons on the dienophile, ultimately forming two new σ-bonds and a π-bond.

Table 1: Molecular Orbitals of Butadiene, Ethylene, and the Transition State

Butadiene - HOMO	Butadiene - LUMO	Ethylene - HOMO	Ethylene - LUMO
TS - HOMO -1	TS - HOMO	TS - LUMO	TS - LUMO +1

MO Diagram Analysis

Fig. 4: MO Diagram of Diels-Alder between butadiene and ethylene

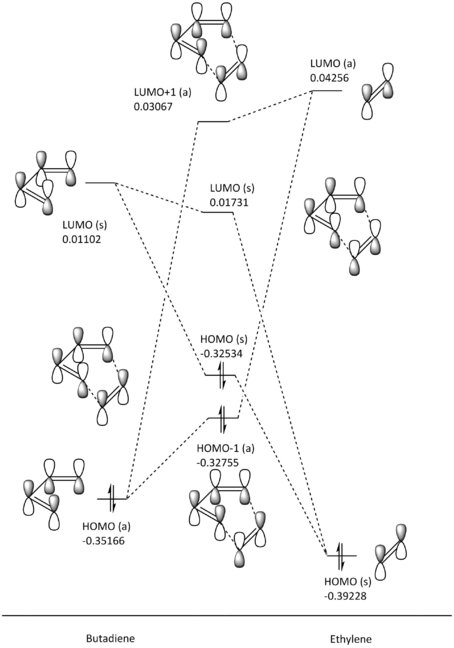
Using the HOMO and LUMO of the two unsaturated reactants, the MOs of the transition state was constructed based on symmetry-restricted interactions, with the relative positions of the MOs based on their energy (in Hartrees) from the optimised structures on Gaussian. The symmetry restriction refers to the fact that only orbitals of the same symmetry (asymmetric with asymmetric and symmetric with symmetric) are "allowed" to interact. For example, the asymmetric HOMO of 1,3-butadiene will interact with the asymmetric LUMO of the ethylene to form two asymmetric MOs (LUMO+1 and HOMO-1) of the transition state, as can be seen in fig. 4. Following the same line of logic, if no orbitals of the same symmetry are present, there will be no favourable orbital interaction available, causing the reaction system to be "disallowed".

The allowed and disallowed interactions can be rationalised by looking at the phase and sign as illustrated on the MO diagram in fig. 4, as well as looking at the overlap integral, a quantitative measure of the overlap of the orbital. Here, the allowed overlaps will lead to constructive interference between the two MO wavefunctions, and a non-zero overlap integral. Conversely, disallowed overlaps will lead to destructive interference between the two MO wavefunctions, and a zero overlap integral.

Conventionally, the MO diagram would show the resulting bonding MO formed to be lower in energy than the two interacting orbitals, while the anti-bonding MO formed would be destabilised instead. However, this is only the case for when it is the more thermodynamically stable product being formed. In this case, we are looking at the formation of the MOs of the transition state, so the transition state HOMO (s) is destabilised relative to the ethylene HOMO (s), as the electron density is delocalised in the energetically strained transition state, causing for the opposite order to be observed.

Table 2: C-C bond length analysis

	C-C Bond Lengths (Å) Raw Data	C=C Bond Lengths (Å) Raw Data	C-C Bond Lengths (Å) 2 dp	C=C Bond Lengths (Å) 2 dp
Butadiene	1.46819 (C2-C3)	1.33531 (C1=C2) 1.33537 (C3=C4)	1.47 (C2-C3)	1.34 (C1=C2) 1.34 (C3=C4)
Ethylene	-	1.32731 (C5=C6)	-	1.33 (C5=C6)
Transition State	1.41109 (C2-C3) 2.11492 (C4-C5) 2.11459 (C6-C1)	1.37980 (C1=C2) 1.37977 (C3=C4) 1.38177 (C5=C6)	1.41 (C2-C3) 2.11 (C4-C5) 2.11 (C6-C1)	1.38 (C1=C2) 1.38 (C3=C4) 1.38 (C5=C6)
Cyclohexene	1.50083 (C1-C2) 1.50083 (C3-C4) 1.53713 (C4-C5) 1.53464 (C5-C6) 1.53713 (C6-C1)	1.33697 (C2=C3)	1.50 (C1-C2) 1.50 (C3-C4) 1.54 (C4-C5) 1.53 (C5-C6) 1.54 (C6-C1)	1.34 (C2=C3)

Table 3: Literature values of typical C-C bond lengths

Typical C-C Bond Length (sp2 )/Å	1.34
Typical C-C Bond Length (sp3)/Å	1.54
Van der Waals Radius of C-atom/Å	1.7

Following the molecular labelling shown in the reaction scheme and the table of C-C bond lengths shown above, we can see the lengthening of the C-C bonds (C1=C2, C3=C4, C5=C6) as it goes from sp² hybridised in the starting olefins (C=C double bonds), through the transition state, to sp³ hybridised in the product (C-C single bonds). This lengthening corresponds to the breaking of the C-C double bonds as their anti-bonding π*-orbitals are being filled in. The difference between the saturated C-C bonds of C1-C2 and C3-C4 (1.50 Å) being shorter than C5-C6 (1.53 Å) is due to the fact that the sp²-sp³ C-C bond length (about 1.50 Å) is shorter compared to sp³-sp³ C-C bond length (about 1.54 Å). The decreasing s-character in the sp² hybrid orbitals

The shortening of the sp³ hybridised C2-C3 single bond can also be seen as it goes through the transition state to the sp² hybridised C2=C3 double bond in the product. Conversely, this is from the forming of the π-bond through the filling of the bonding π-orbital between C2 and C3. The two new σ-bonds formed between C4-C5 and C6-C1 can also be seen as their bond lengths in transition state (2.11 Å) closely resembles the expected bond length which is somewhere between the sum of the two Van der Waals radius of the C-atom (3.4 Å), and the sp³-sp³ C-C bond length (1.54 Å). These σ-bonds formed are also of the expected length (1.54 Å) in the product.

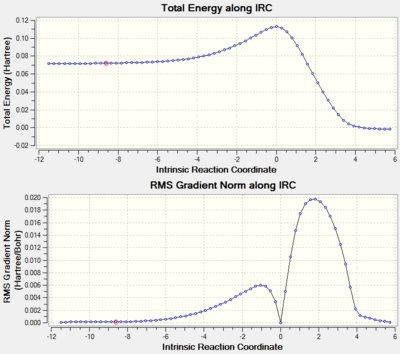
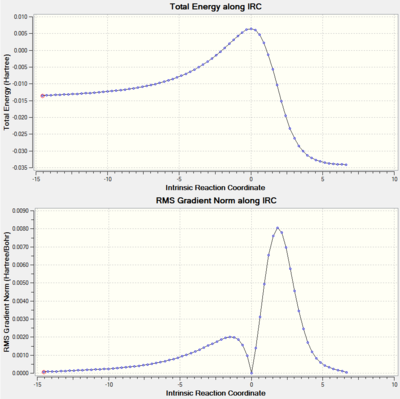
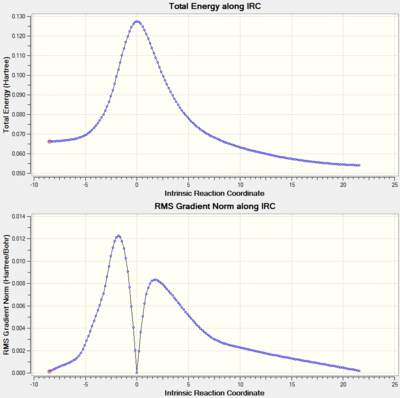
It should also be noted that the C-C bond lengths for the transition states are all closer to those of the starting materials than those of the product; for example, C1-C2 is 1.38 Å in the transition state, which is 0.04 Å larger than C1-C2 in butadiene (1.34 Å), and 0.12 Å smaller than C1-C2 in the product cyclohexene (1.50 Å). Following Hammond's postulate, this suggests that the transition state is an early transition state, where the structure of the transition state is closer to that of the reactants than that of the product. This is confirmed by the IRC graph shown below, whereby the transition state is clearly much closer in energy to the reactants compared to the product.

Intrinsic Reaction Coordinate (IRC)

Graph	Animation
Graphs of Total Energy against IRC (TOP) and its First Derivative (BOTTOM) for Diels-Alder Reaction between Butadiene and Ethylene	Diels-Alder Reaction of Butadiene and Ethylene (Animated)

Vibrational Analysis

The transition state vibration shown above corresponds to the imaginary (negative) vibrational frequency, showing a synchronous bond formation between the two olefins, as expected of a concerted mechanism of cyclisation. The concerted nature of the bond-formation can also be seen in the animation of the IRC analysis, where the two C-C σ-bonds can be seen to form at the same time at the terminal carbon atoms of butadiene and ethylene; the two reactants also approach one another at the same rate, further supporting the idea of synchronous bond-formation.

LOG Files

File:BUTADIENE_OPTIMISE_FREQ_MINIMISE_1.LOG

File:BUTADIENE_OPTIMISE_FREQ_MO_1.LOG

File:ETHYLENE_OPTIMISE_FREQ_MINIMISE_1.LOG

File:ETHYLENE_OPTIMISE_FREQ_MO_1.LOG

File:1-HEXENE_OPTIMISE_FREQ_MINIMISE_1.LOG

File:1-HEXENE_OPTIMISE_FREQ_MINIMISE_1_IRC.LOG

File:1-HEXENE_OPTIMISE_FREQ_MINIMISE_TRY2_1.LOG

File:1-HEXENE_OPTIMISE_FREQ_MO_TRY2_3.LOG

File:1-HEXENE_OPTIMISE_FREQ_TS_BERNY_TRY2_1.LOG

File:1-HEXENE_OPTIMISE_FREQ_TS_BERNY_TRY2_2.LOG

File:1-HEXENE_OPTIMISE_FREQ_TS_BERNY_TRY2_2_IRC.LOG

File:1-HEXENE_OPTIMISE_FREQ_TS_BERNY_TRY2_3.LOG

File:1-HEXENE_OPTIMISE_FREQ_TS_BERNY_TRY2_3_IRC.LOG

File:PRODUCT_1-HEXENE_OPTIMISE_FREQ_MINIMISE_1.LOG

Exercise 2: Reaction of Cyclohexadiene and 1,3-Dioxole

Fig. 5: Reaction pathways of Cyclohexadiene and 1,3-Dioxole

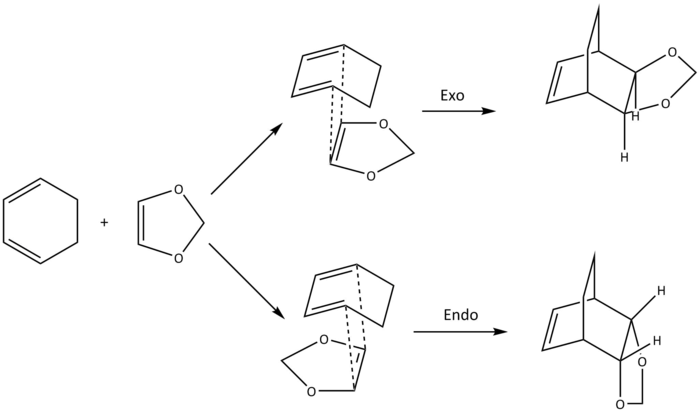
Using calculation method 3 as outlined in the introduction, the [4+2] Diels-Alder cycloaddition of cyclohexadiene and 1,3-dioxole was investigated. Depending on the approach of the diene and dienophile towards one another, there were two possible pathways for this reaction, with each of the approach (exo and endo) giving two products with different stereochemistry and thermodynamic stability. Initially, the structure of each of the exo and endo products were made and minimised to the PM6 and then the B3LYP/6-31(d) level. The relevant bonds in the minimised products were then broken and frozen at appropriate distances (2.2 Å for C-C bonds), and were once again minimised to the PM6 level. With the bonds now unfrozen, optimisations to the transition state at the PM6 and the subsequent B3LYP/6-31(d) level were then carried out, before being put under an IRC calculation.

MO Diagram Analysis

(Fv611 (talk) Good MO diagrams but you could have discussed the difference between endo and exo conformation in terms of relative MO energies)

Exo Diels-Alder MO Diagram	Endo Diels-Alder MO Diagram
Fig. 6: MO Diagram for Exo-approach	Fig. 7: MO Diagram for Endo-approach

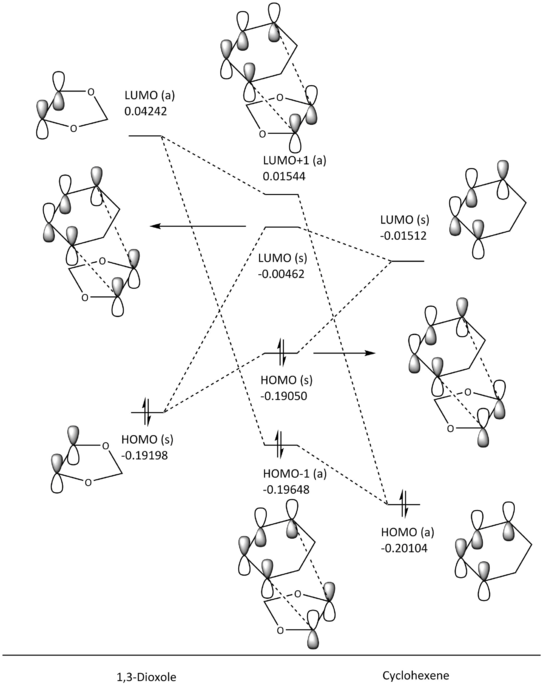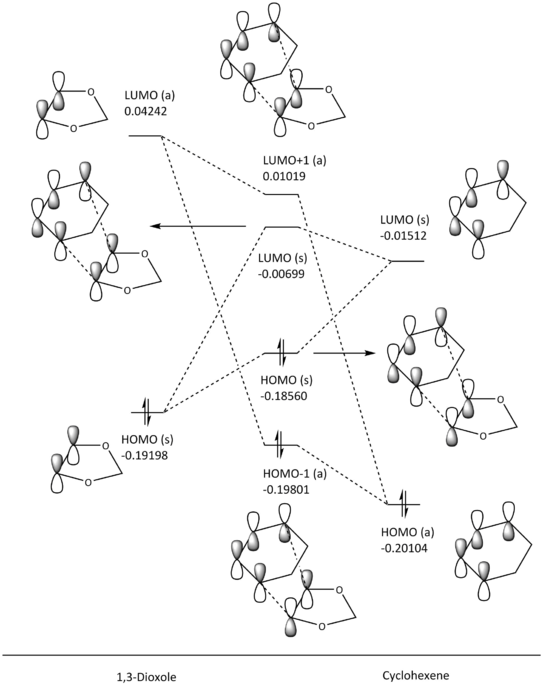
With this pericyclic reaction, cyclohexadiene is acting as the diene, while the 1,3-dioxole is the dienophile. From the MO diagrams above (fig. 6 and 7), the interacting orbitals that form the HOMO (s) and LUMO (s) bonding-antibonding pair of the transition state are the HOMO of the dienophile and the LUMO of the diene, which goes against the order of normal electron demand (HOMO from electron-rich diene and LUMO from electron-poor dienophile). This is most likely due to the oxygen atoms on 1,3-dioxole donating electron density into the C-C double bond, increasing the energy of the HOMO (s). This makes the cycloaddition reaction occur under inverse electron demand, where the dienophile is the electron rich component instead of the diene. Following the Woodward-Hoffmann rules, this pericyclic reaction is still thermally viable since (4q+2)_s + (4r)_a gives an odd number, as there is only one (4q+2)_s component, and no (4r)_a component.

Nf710 (talk) 23:29, 5 March 2018 (UTC)TGoood understanding of the woodwood-hoffman rules, but your argument of electron demand is not backed up by by any evidence. you can explore this quantitatively by doing a single point energy calc on the reactants.

Table 4: Molecular Orbitals of the Exo and Endo Transition States

EXO TS (HOMO -1, E = -0.19801)	EXO TS (HOMO, E = -0.18560)	EXO TS (LUMO, E = -0.00699)	EXO TS (LUMO +1, E = 0.01019)

ENDO TS (HOMO -1, E = -0.19648)	ENDO TS (HOMO, E = -0.19050)	ENDO TS (LUMO, E = -0.00462)	ENDO TS (LUMO +1, E = 0.01544)

Thermochemical data

Table 5: Thermochemical data of the exo and endo pathways of [4+2] cycloaddition of Cyclohexadiene and 1,3-Dioxole

	Activation energy/ Hartrees	Activation energy/ kJmol-1	Reaction Energy/ Hartrees	Reaction Energy/ kJmol-1
Exo Pathway	0.060002	157.54	-0.028157	-73.93
Endo Pathway	0.057013	149.69	-0.029527	-77.52

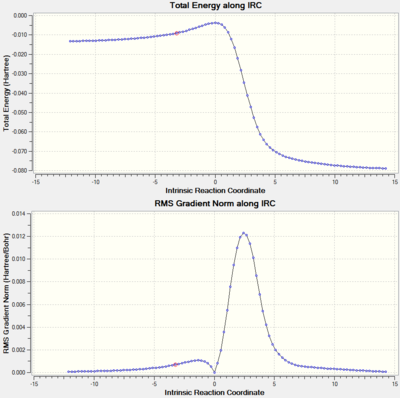
Reaction Profile

Fig. 8: Reaction profile for the two pathways of the Diels-Alder reaction between Cylohexadiene and 1,3-Dioxole

From the MO diagrams (fig. 6 and 7) and the reaction profile (fig. 8), it can be seen that the endo transition state is lower in energy than that of the exo transition state, making the endo product the kinetic product. The calculated thermochemical data tabulated above (Table 5) also shows the activation energy for the endo pathway to be less positive compared to that of the exo pathway. This can be rationalised by looking at the frontier orbitals of the endo-approach (fig. 9), which shows secondary orbital interaction between the oxygen lone pair and the developing π-bond, stabilising the endo transition state, as shown below.

Fig. 9: Secondary orbital overlap of the oxygen lone pair and the new π-bond

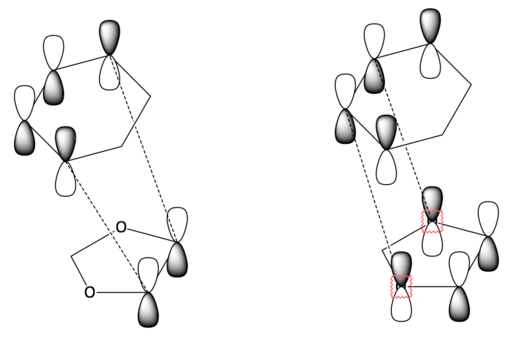
Exo HOMO Secondary Interactions	Endo HOMO Secondary Interactions

The thermochemical data on table 5 also shows the reaction energy for the endo product to be more negative than that of the exo product, while the reaction profile (fig. 8) helps further illustrate that the endo product is more thermodynamically stable. This can be rationalised by the absence of steric clash between the cyclohexadiene bridge and the 1,3-dioxole ring as they are on opposite faces, which is not the case for the exo product (as shown in fig. 10 below). Note that the secondary orbital interactions previously mentioned and illustrated in fig. 9 still plays a part in the stabilisation of the endo product.

Fig. 10: Absence of steric clash in the endo product and presence of steric clash in the exo product

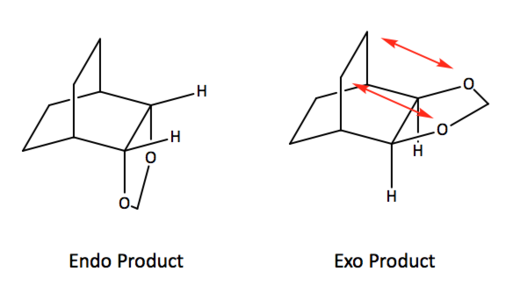
Nf710 (talk) 23:31, 5 March 2018 (UTC) You should have drawn the hydrogens in your steric clash. Your energies are slightly out but you have still come to the correct conclusions. Good section but there were a few part which you could have investigated in more detail

LOG Files

File:CYCLOHEXADIENE_DIOXOLE_ENDO_OPT_FREQ_MINIMISE_B3LYP.LOG

File:CYCLOHEXADIENE_DIOXOLE_ENDO_OPT_FREQ_MINIMISE_PM6.LOG

File:CYCLOHEXADIENE_DIOXOLE_ENDO_OPT_FREQ_MINIMISE_PM6_2.LOG

File:CYCLOHEXADIENE_DIOXOLE_ENDO_OPT_FREQ_MINIMISE_PM6_3.LOG

File:CYCLOHEXADIENE_DIOXOLE_ENDO_OPT_FREQ_MINIMISE_PM6_4.LOG

File:CYCLOHEXADIENE_DIOXOLE_ENDO_OPT_FREQ_TS_B3LYP_MO.LOG

File:CYCLOHEXADIENE_DIOXOLE_ENDO_OPT_FREQ_TS_IRC.LOG

File:CYCLOHEXADIENE_DIOXOLE_ENDO_OPT_FREQ_TS_IRC2.LOG

File:CYCLOHEXADIENE_DIOXOLE_ENDO_OPT_FREQ_TS_PM6.LOG

File:CYCLOHEXADIENE_DIOXOLE_EXO_OPT_FREQ_MINIMISE_B3LYP.LOG

File:CYCLOHEXADIENE_DIOXOLE_EXO_OPT_FREQ_MINIMISE_PM6.LOG

File:CYCLOHEXADIENE_DIOXOLE_EXO_OPT_FREQ_MINIMISE_PM6_2.LOG

File:CYCLOHEXADIENE_DIOXOLE_EXO_OPT_FREQ_TS_B3LYP.LOG

File:CYCLOHEXADIENE_DIOXOLE_EXO_OPT_FREQ_TS_IRC.LOG

File:CYCLOHEXADIENE_DIOXOLE_EXO_OPT_FREQ_TS_MO.LOG

File:CYCLOHEXADIENE_DIOXOLE_EXO_OPT_FREQ_TS_PM6.LOG

File:CYCLOHEXADIENE_OPT_FREQ_MINIMISE_B3LYP_MO.LOG

File:CYCLOHEXADIENE_OPT_FREQ_MINIMISE_PM6.LOG

File:DIOXOLE_OPT_FREQ_MINIMISE_B3LYP_MO.LOG

File:DIOXOLE_OPT_FREQ_MINIMISE_PM6.LOG

Exercise 3: Diels-Alder vs Cheletropic

Fig. 11: Reaction pathways of o-Xylylene with SO₂

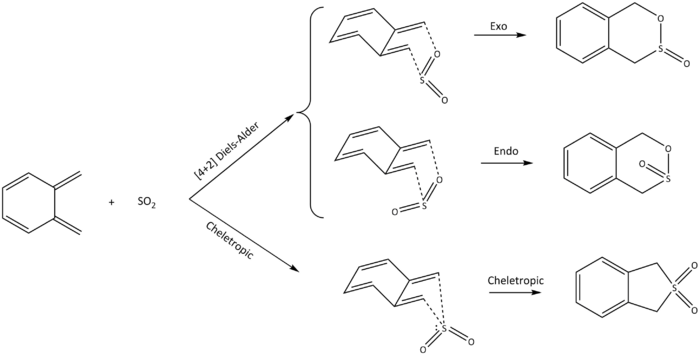
(Xylylene is still planar Tam10 (talk) 13:08, 2 March 2018 (UTC))

Once again, using calculation method 3, the [4+2] Diels-Alder cycloaddition between o-xylylene and SO₂ was analysed. The pericyclic reaction has three pathways when cyclising at the terminal diene of o-xylylene, which includes the exo and endo approach (Diels-Alder), as well as the cheletropic approach. Similarly to exercise 2, the structure of each of the products were first constructed and minimised, taken apart where the bonds were being formed and subsequently frozen, optimised to a transition state, and finally having an IRC calculation done on the optimised structure. The difference is that all calculations were only done up to the PM6 level compared to exercise 2, where the hybrid B3LYP/6-31 (d) calculation was also used.

Intrinsic Reaction Coordinate (IRC)

Exo:

Graph	Animation
Graphs of Total Energy against IRC (TOP) and its First Derivative (BOTTOM) for Diels-Alder Reaction between o-Xylylene and SO2	Fig. 12: Diels-Alder Reaction of o-Xylylene and SO2 (Animated)

Endo:

Graph	Animation
Graphs of Total Energy against IRC (TOP) and its First Derivative (BOTTOM) for Diels-Alder Reaction between o-Xylylene and SO2	Fig. 13: Diels-Alder Reaction of o-Xylylene and SO2 (Animated)

Cheletropic:

Graph	Animation
Graphs of Total Energy against IRC (TOP) and its First Derivative (BOTTOM) for Diels-Alder Reaction between o-Xylylene and SO2	Fig. 14: Diels-Alder Reaction of o-Xylylene and SO2 (Animated)

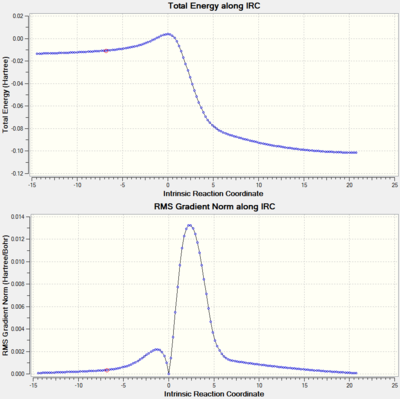
The IRCs above show the three different routes the SO₂ molecule can add to the terminal diene of o-xylylene. The Diels-Alder approach (exo and endo, fig. 12 and 13, respectively) shows asynchronous bond formation between SO₂ and o-xylyene as the C-O σ-bond forms before the C-S σ-bond in both the exo and endo pathways. In contrast, the cheletropic addition (fig. 14) shows synchronous bond formation of the sulfur atom on SO₂, as the two C-S bonds on the terminal diene forms at the same time.

Thermochemical Data

Table 6: Thermochemical Data of the Diels-Alder (endo and exo) and Cheletropic pathways for the addition of o-Xylylene and SO₂

	Activation Energy/ Hartrees	Activation Energy/ kJmol-1	Reaction Energy/ Hartrees	Reaction Energy/ kJmol-1
Exo	0.033303	87.44	-0.033548	-88.08
Endo	0.031785	83.45	-0.032288	-84.77
Cheletropic	0.040286	105.77	-0.058770	-154.30

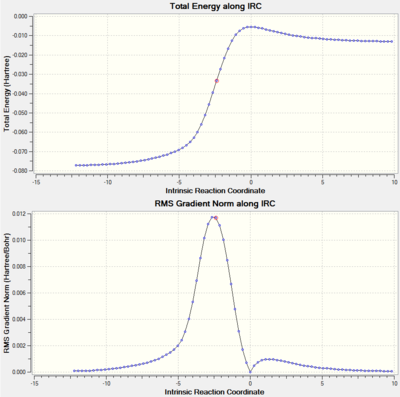
Reaction Profile

Fig. 15: Reaction profile for the three pathways of the Diels-Alder reaction between o-Xylylene and SO₂

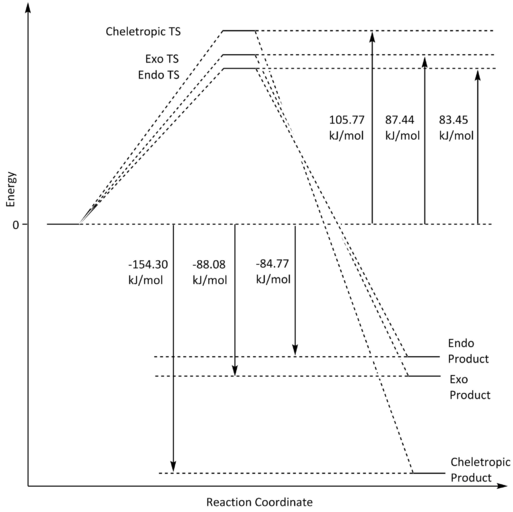
From the tabulated thermochemical data on table 6, we can see that, although it also has the highest activation energy barrier, the cheletropic pathway has the highest (most negative) reaction energy. The high energy transition state of the cheletropic pathway can be rationalised by the five-membered ring strain experienced, which is a more energetically burdened state compared to the six-membered ring transition states of the Diels-Alder pathways. The fact that the cheletropic product is the most thermally stable is most likely due to the fact that it still has two strong S=O bonds (522 kJmol^-1) compared to the Diels-Alder products which only have one S=O bond left over while the other was cleaved during the cyclisation.

Looking at the two competing Diels-Alder pathways on table 6 and fig. 15, the endo pathway is the kinetic pathway as its activation energy is smaller. This is due to similar reasons as discussed for exercise 2, whereby the endo transition state receives additional stabilisation from the secondary orbital interactions between the lone pair of electrons on the oxygen that isn't directly involved in the pericyclic mechanism, and the π-orbitals of the second set of unsaturation in o-xylylene; this overlap is not available for the exo mechanism due to the fact that the oxygen lone pair that would interact is too far away.

Alternative Diels-Alder Pathway

Fig. 16: Alternative reaction pathway for Diel-Alder of o-Xylylene with SO₂

IRC for Alternative Diels-Alder Pathway

Exo:

Graph	Animation
Graphs of Total Energy against IRC (TOP) and its First Derivative (BOTTOM) for the alternative Diels-Alder Reaction between o-Xylylene and SO2	Fig. 17: Alternative Diels-Alder Reaction of o-Xylylene and SO2 (Animated)

Endo:

Graph	Animation
Graphs of Total Energy against IRC (TOP) and its First Derivative (BOTTOM) for the alternative Diels-Alder Reaction between o-Xylylene and SO2	Fig. 18: Alternative Diels-Alder Reaction of o-Xylylene and SO2 (Animated)

Thermochemical Data for Alternative Diels-Alder Pathway

Table 7: Thermochemical Data of the alternative Diels-Alder (endo and exo) pathways for the addition of o-Xylylene and SO₂

	Activation Energy/ Hartrees	Activation Energy/ kJmol-1	Reaction Energy/ Hartrees	Reaction Energy/ kJmol-1
Exo	0.04628	121.51	-0.00853	-22.40
Endo	0.043295	113.67	-0.006836	-17.95

Other than the three pathways mentioned, there are two additional Diels-Alder pathways (exo and endo) for the pericylic addition of SO₂ to o-xylylene, where the diene in the cyclohexadiene ring in o-xylylene acts as the diene undergoing cycloaddition instead. The IRC analysis of the exo and endo approaches (fig. 17 and 18) shows asynchronous σ-bond formation with the C-O bond forming first; the same as for the exo and endo approaches to the terminal diene seen before. Looking at its thermochemical data on table 7, in comparison to the values on table 6 and fig. 15, we can see that while the relative energies of the exo and endo approaches are the same (exo is the thermodynamic pathway while endo is the kinetic pathway), the activation energy for this alternative approach is higher (more positive) than those of the previous approach, and its reaction energies are also lower (less negative). The higher activation barrier is possibly due to the transition state being more strained due to the hindered trajectory of approach for this particular pericyclic mechanism. The lower reaction energies are most likely due to the alternative products being less thermally stable from the lack of formation of an aromatic system which forms for the original Diels-Alder pathway in the form of a benzene ring. So although this alternative pathway is thermodynamically viable (negative reaction energies), it is not very favourable for these less stable products to form, not to mention the more energy required to overcome the higher activation barrier; thus the formation of these alternative pericyclic products are not as favourable, and also slower than the original pathways.

LOG Files

File:XYLYLENE-SO2_OPT_FREQ_MINIMISE_1.LOG

File:XYLYLENE-SO2_OPT_FREQ_MINIMISE_2.LOG

File:XYLYLENE-SO2_OPT_FREQ_TS_2.LOG

File:XYLYLENE-SO2_OPT_FREQ_TS_2_IRC.LOG

File:XYLYLENE-SO2_OPT_FREQ_TS_3_PM6.LOG

File:XYLYLENE-SO2_OPT_FREQ_MINIMISE_2_ENDO.LOG

File:XYLYLENE-SO2_OPT_FREQ_MINIMISE_3_ENDO.LOG

File:XYLYLENE-SO2_OPT_FREQ_TS_2_ENDO.LOG

File:XYLYLENE-SO2_OPT_FREQ_TS_2_IRC_ENDO.LOG

File:XYLYLENE-SO2_OPT_FREQ_TS_2_IRC2_ENDO.LOG

File:XYLYLENE-SO2_OPT_FREQ_MINIMISE_1_EXO.LOG

File:XYLYLENE-SO2_OPT_FREQ_MINIMISE_2_EXO.LOG

File:XYLYLENE-SO2_OPT_FREQ_TS_2_EXO.LOG

File:XYLYLENE-SO2_OPT_FREQ_TS_2_IRC_EXO.LOG

File:XYLYLENE-SO2_V2_OPT_FREQ_MINIMISE_1_ENDO.LOG

File:XYLYLENE-SO2_V2_OPT_FREQ_MINIMISE_2_ENDO.LOG

File:XYLYLENE-SO2_V2_OPT_FREQ_TS_1_ENDO.LOG

File:XYLYLENE-SO2_V2_OPT_FREQ_TS_1_IRC_ENDO.LOG

File:XYLYLENE-SO2_V2_OPT_FREQ_MINIMISE_1_EXO.LOG

File:XYLYLENE-SO2_V2_OPT_FREQ_MINIMISE_2_EXO.LOG

File:XYLYLENE-SO2_V2_OPT_FREQ_TS_1_EXO.LOG

File:XYLYLENE-SO2_V2_OPT_FREQ_TS_1_IRC_EXO.LOG

File:SO2_OPT_FREQ_MINIMISE_1.LOG

File:SO2_OPT_FREQ_MINIMISE_2.LOG

File:XYLYLENE_OPT_FREQ_MINIMISE_1.LOG

File:XYLYLENE_OPT_FREQ_MINIMISE_2.LOG

Extension: Electrocylic Ring-Opening of 1,2-Dibromocyclobutene

Electrocyclic Ring-Opening of 1,2-Dibromocyclobutene

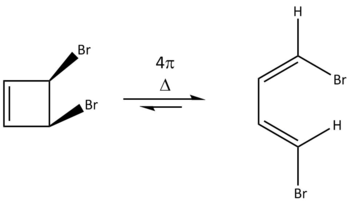
Similarly to the investigation done in exercise 3, the structure of the ring-opened product was first minimised, before being taken apart with their relevant bonds frozen (and minimised once again), and then optimised to a transition state; an IRC calculation was also done on the optimised transition state structure. All calculations were done on the PM6 level. Although this thermal electrocyclic ring-opening is equilibrated with the ring-opened form being the more favourable state due to the ring-strain present in the cyclised form, the ring-closing reaction will be investigated (via Woodward-Hoffmann methods) and taken as the forward reaction.

Table 8: MO Analysis

TS (HOMO, E = -0.34709)	TS (LUMO, E = -0.03179)	1,4-Dibromo-butadiene (HOMO, E = -0.35498)	1,4-Dibromo-butadiene (LUMO, E = -0.02391)

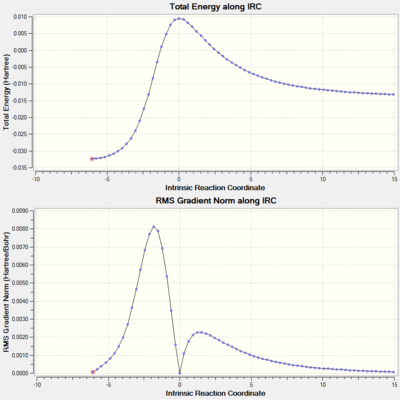
Intrinsic Reaction Coordinate (IRC)

1,2-Dibromocyclobutene Electrocyclic Ring-Opening:

Graph	Animation
Graphs of Total Energy against IRC (TOP) and its First Derivative (BOTTOM) for Electrocyclic Ring-Opening of 1,2-Dibromocyclobutene	Fig. 19: Electrocyclic Ring-Opening of 1,2-Dibromocyclobutene (Animated)

Mechanistic Analysis

Fig. 20: Woodward-Hoffmann analysis of the electrocyclic ring-closing mechanism (thermally driven)

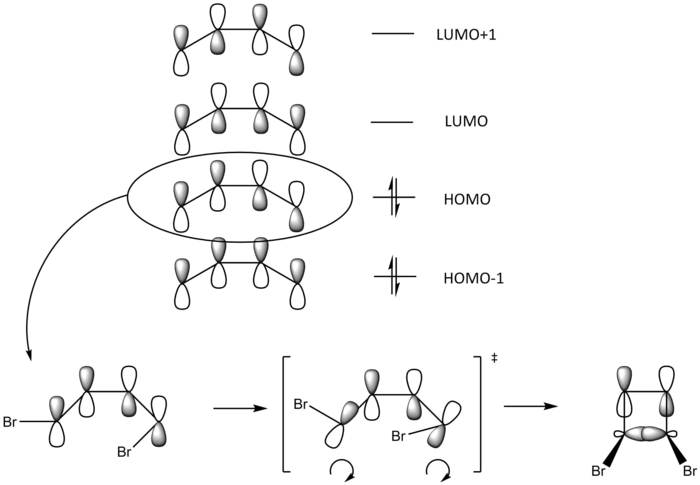
Looking at the HOMO of the ring-opened 1,4-dibromo-butadiene from table 8 and fig. 20, we can see that the conratory transition state of this electrocyclic ring-closing process has a C₂ axis of symmetry in the middle of the molecule, giving a favourable orbital overlap (bonding) compared to its disrotatory counterpart (antibonding). The 4π conjugated system of the 1,3-butadiene, with antarafacial relationship of the bond topology, gives a Woodward-Hoffmann notation of [_π4_a] for the system. Using this with (4q+2)_s + (4r)_a gives no (4q+2)_s component and one (4r)_a component, as the integer r = 1. This overall odd value of the general relationship means that this conrotatory ring-closing mechanism is thermally allowed.

(This reaction goes via a Mobius aromatic TS where most if not all relevant orbitals rotate to some extent, allowing a swap of symmetry. The product orbital that you've provided wouldn't actually exist where the front has a different symmetry to the back. Unfortunately the wiki article is wrong about this Tam10 (talk) 14:08, 2 March 2018 (UTC))

LOG Files

File:CYCLOBUTENE_BR_PRODUCT_OPT_FREQ_MINIMISE_PM6.LOG

File:CYCLOBUTENE_BR_OPT_FREQ_MINIMISE_MO_PM6.LOG

File:CYCLOBUTENE_BR_OPT_FREQ_MINIMISE_PM6.LOG

File:CYCLOBUTENE_BR_OPT_FREQ_MINIMISE_PM6_2.LOG

File:CYCLOBUTENE_BR_OPT_FREQ_TS_MO_PM6.LOG

File:CYCLOBUTENE_BR_OPT_FREQ_TS_MO_PM6_2.LOG

File:CYCLOBUTENE_BR_TS_PM6_IRC.LOG

Conclusion

Using Gaussian and its PM6 and B3LYP calculation methods, the reaction processes of four different pericyclic reactions were investigated via geometric calculations of their optimised reactants, products, and transition states. In the first exercise, all optimisations were done up to the PM6 level, where the thermochemical data and molecular orbitals of the reactants and transition states were analysed. The obtained bond lengths of the reactants and product aligned closely to the expected literature values, and the IRC analysis showed the cycloaddition process to have an early transition state, and synchronous σ-bond formation. Exercise two had optimisations done up to the hybrid B3LYP level after the PM6 optimisations, the thermochemical data results indicated an inverse electron demand reaction. The endo pathway led to both the kinetic and thermodynamic product, rationalised by the secondary orbital interactions and steric arguments. The third exercise, like the first exercise, used only the PM6 calculations to investigate the Diels-Alder and chelotropic pathways. From the thermochemical data obtained, the endo product is the kinetic product, while the cheletropic product is the thermodynamic product. Its IRC analysis showed that both the exo and endo cycloadditions occurred via asynchronous σ-bond formations, while the cheletropic mechanism went through synchronous σ-bond formations. The extension carried out looked at the thermal electrocyclic ring-opening of 1,2-dibromocyclobutene, optimising only up to the PM6 level. Analysis with the Woodward-Hoffmann approach on the ring-closing of the 1,3-butadiene derivative gave a thermally allowed 4π conrotatory mechanism.