Rep:Mod:kitten
Introduction
In this report, the transition structures were investigated for two pericyclic reactions: the Cope Rearrangement (Part 1) and the Diels-Alder cycloaddition (Part 2). These calculations were carried out using Gaussview and Gaussian using the following methods:
- HF/3-21G
- B3LYP/6-31G*
- AM1
In addition to showing the HOMO and LUMO surfaces of the transition structures, the reaction pathways and activation energies were investigated and compared to available experimental data. Calculations are shown in the log files provided.
Part 1: The Cope Rearrangement
(Tutorial section - have to include in write up, giving answers, documentation proof, discussion and how any problems encountered were solved.)
The Cope Rearrangement is defined in IUPAC as the [3,3] sigmatropic rearrangement of 1,5-diene. [1] and a reaction scheme is shown below.

In the following section, the lowest energy conformations (anti or gauche) and the transition state structures (chair or boat) for 1,5-hexadiene are investigated. The calculation methods used will be HF/3-21G at first then further calculated at a higher level of theory using B3LYP/6-31G*.
Optimising the Reactants and Products
Anti-1,5-hexadiene

In Gaussview, the anti 1,5-hexadiene structure was drawn and cleaned. The molecule was then optimised using the Hartree-Fock calculation method and the 3-21G basis set. The energy energy is noted below along with the point group (after symmetrising the structure in Gaussview). This data corresponded in the appendix provided in the physical computational wiki page to identify the molecule as "anti1".
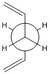
Gauche-1,5-hexadiene
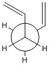
The above method was repeated using the gauche 1,5-hexadiene structure and the energy was compared to the anti conformation in the table below. The data was compared with the data provided in the physical computational wiki page to suggest that the "gauche3" structure had been formed.
When considering sterics, it could be suggested that anti would be the lowest energy conformation but the gauche has a lower energy conformation as a result of favourable electronic factors. This is supported in literature [2] where a favourable interaction between the proton on the alkene and the π orbital is given as a possible explanation.
Comparison of lowest energy conformations of 1,5-hexadiene
| Conformation | Energy (Hartrees) | Point Group |
|---|---|---|
| Anti | -231.69260 | C2 |
| Gauche | -231.69266 | C1 |
The energy was found to be -231.69260 and the point group to be C2 therefore the molecule was identified as "anti1" in the appendix table provided which has very close agreement.
The energy was found to be -231.69266 and the point group to be C1 therefore the molecule was identified as "gauche3".
From comparing the above data, it would be assumed that the lowest energy conformation would be the gauche conformation and due to steric factors, it would be more favourable for the end groups to be leaning away from each other and the protons on the central atoms facing opposite directions.
These conditions appear to be satisfied by the "gauche3" structure identified above and further attempts gave the same structure after optimisation using HF/3-21G. This was confirmed by comparison to the structures in the appendix provided which indicated "gauche3" was the lowest energy conformation.
Anti-1,5-hexadiene with Ci symmetry
Another anti-1,5-hexadiene structure was drawn with Ci point group symmetry and optimised at the HF/3-21G level of theory. The energy values obtained held good agreement with the energy value given in the appendix and appeared to have the same structure as the structure in the appendix therefore this was optimised at a higher level of theory (B3LYP/6-31G*).
| Characteristic | Data given in appendix | HF/3-21G | B3LYP/6-31G* |
|---|---|---|---|
| Energy (Hartrees) | -231.69254 | -231.69254 | -234.61170 |
| Terminal C=C bond lengths (Å) | - | 1.316 | 1.334 |
| =C-C- bond lengths (Å) | - | 1.509 | 1.504 |
| Central C-C bond lengths (Å) | - | 1.553 | 1.548 |
| C=C-C dihedral angle (°) | - | 124.8 | 125.3 |
| C-C-C dihedral angle (°) | - | 111.3 | 112.7 |
There does not appear to be a significant difference in the geometry though the reoptimised structure contains longer C=C double bonds and shorter C-C bonds and larger dihedral angles yet the energies have changed by 1831.8 kcalmol-1 which is surprising given the comparably small difference in geometry.
A frequency calculation was then run in order to show the vibrations and a simulated infrared spectrum. Energies are also given that can be compared to experimental values (free energies, enthalpies and entropies). The values given are provided in the table below.

| Energy (kcal mol-1) | |
|---|---|
| Sum of electronic and zero-point energies | -234.469212 |
| Sum of electronic and thermal energies | -234.461856 |
| Sum of electronic and thermal enthalpies | -234.460912 |
| Sum of electronic and thermal free energies | -234.500822 |
Optimising the Transition Structures
In this section, three methods for optimising the transition structure are explored:
- Computing the force constants (using TS Berny optimisation)
- Using the frozen coordinate method
- Using QST2
The 'Chair' Transition Structure for 1,5-hexadiene
The chair structure was drawn first by drawing a single allyl fragment and optimising using the HF/3-21G level of theory. Two of these optimised structures were then appended together then orientated in the chair transition state orientation. The distances between the terminal ends were set to 2.2Å apart.
This chair structure was optimised in using two of the above methods all under the Hartree Fock and default basis set 3-21G.
Computing the force constants (TS Berny optimisation)
An optimisation and frequency calculation was carried out for the chair transition structure by optimising to TS(Berny) instead of optimising to a minimum. The force constants were set to calculate once and an additional keyword Opt=NoEigen was added in order to stop the calculation failing if more than one imaginary frequency was detected. However, only one imaginary frequency was detected at 818 cm-1 which was as expected. The vibration is shown by the gif to be corresponding to the Cope rearrangement.
Using the frozen coordinate method
Using the chair structure, the Redundant Coord Editor in Gaussview and new bond coordinate distances were added then frozen in separate inputs. The optimisation was then run as if it were to a minimum (ensuring that the Opt=ModRedundant was in the input line) in order to find the lowest energy structure for the unfrozen coordinates. After the optimisation had finished, the bonds that were previously frozen were selected in the Redundant Coord Editor and instead of Unidentified, Bond was chosen and Derivative instead of Add. A transition state optimisation was set up with the force constants set to Never so that calculation of the Hessian matrix is avoided.
The 'Boat' Transition Structure for 1,5-hexadiene
Using the QST2 method
This method involves specifying the reactants and products for a reaction which is then used in the calculation to interpolate between the structures to locate the transition state structure. First of all, the boat structure was created by pasting the Ci structure into a window. This was copied and pasted into another window (in the same MolGroup) but with inversion so that the two geometries could be compared side by side (representing the reactant and the product). The atoms in the reactants and products were required to be labelled in the same way by opening View then Label then the Atom List in the Edit menu.
The job type was set to Opt+Freq and the transition structure was optimised to TS (QST2). However, this job did not run successfully. For both the product and reactant, the dihedral angles for the central four carbons were edited to 0° and the non-terminal three carbons' angles were set to 100°. The QST2 calculation was then run again to give the boat transition structure with one imaginary frequency at 840cm-1. This is due to the original reactant and product not resembling the boat transition structure sufficiently for a QST2 optimisation to be run (where the purpose of changing the angles was to make the reactant and product more 'boat'-like).
Intrinsic Reaction Coordinate method
The IRC method shows the minimum energy path from a transition state to a local minimum by taking small steps towards a geometry where the gradient of the energy surface is the steepest. This method was carried out on the chair transition structure optimised using the method involving calculating force constants.
IRC was selected as the Job Type and the reaction coordinate was computed in the forward direction (as it is symmetrical) with force constants calculated always. The maximum number of points was set to 1000 to ensure that a minimum was reached.
The gif file shows the reaction pathway and the IRC plot is also shown, indicating that a minimum had been reached at 14 steps.
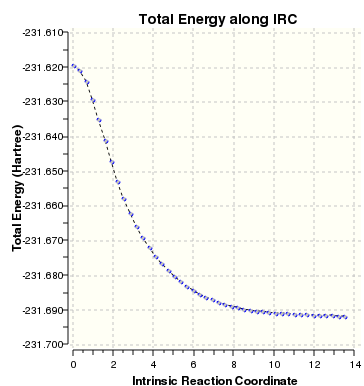
File:CHAIRTSGUESSV1IRCATTEMPT1.LOG
Calculating the activation energies via 'chair' and 'boat' transition structures
From this point, the level of theory used for calculations was increased to use the B3LYP/6-31G* level of theory (optimising to TS Berny) starting from the structures that had already been optimised by the HF/3-21G calculation method. These structures were compared and showed that (similar to the anti Ci structure in a previous section), the geometries did not appear to have changed significantly but there was a noticeable difference in the energies.
| HF/3-21G | B3LYP/6-31G* | |||
|---|---|---|---|---|
| Electronic and zero-point energies | Electronic and thermal energies | Electronic and zero-point energies | Electronic and thermal energies | |
| Chair (from Berny TS) | -231.466701 | -231.461341 | -234.414929 | -234.409009 |
| Chair (from frozen coordinates) | -231.466705 | -231.461345 | -234.414934 | -234.409011 |
| Boat | -231.450930 | -231.445301 | -234.402343 | -234.396008 |
| Anti (Reactant) | -231.539539 | -231.532566 | -234.469212 | -234.461856 |
File:CHAIRTSGUESSV1REOPT.LOG File:CHAIRTSGUESSV2CONTREOPT.LOG File:BOATTSREOPTBERNY.LOG
Considering the energies of chair transition structures from different methods, the energies are close enough to consider the chair transition state in general. As both methods gave similar data, it can be assumed that this is an accurate representation of the chair transition state.
| Transition state structure | HF/3-21G (0 K) | HF/3-21G (298.15 K) | B3LYP/6-31G* (0 K) | B3LYP/6-31G* (298.15 K) | Experimental (at 0 K) |
|---|---|---|---|---|---|
| Chair | 45.7 | 44.7 | 34.1 | 33.2 | 33.5 ± 0.5 |
| Boat | 55.6 | 54.8 | 42.0 | 41.3 | 44.7 ± 2.0 |
From comparing the activation energies to the experimental values given in the appendix of the Y3 Physical Computational wiki, the results at the higher level of theory are close to the energies expected but are slightly out of the accepted range. This method does not consider factors like solvation which would affect the experimental result and could be the result of this small difference. The activation energies at HF/3-21G level of theory are well out of the accepted range but does show the expected trend that the chair has a lower activation energy than the boat.
Part 2: The Diels Alder Cycloaddition
A cycloaddition is defined in IUPAC as a reaction in which two or molecules with unsaturated bonds come together to form a cycloadduct. The Diels Alder reaction is an example of a (4+2) cycloaddition involving a diene and a dienophile.[1]
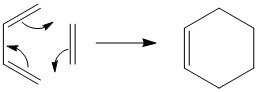
All the following calculations were carried out at AM1 semi-empirical molecular orbital method.
Cis butadiene
The HOMO and LUMO of cis butadiene are shown below after optimisation to a minimum in Gausssian with their corresponding symmetries in relation to the plane, which is as expected.
| HOMO | LUMO | |
|---|---|---|
| Image |  |

|
| Symmetry with respect to plane | antisymmetric | symmetric |
Transition State Geometry for Simple Diels-Alder Reaction
The ethene MOs were also investigated and the symmetries reported in the table below.
| HOMO | LUMO | |
|---|---|---|
| Image |  |

|
| Symmetry with respect to plane | symmetric | antisymmetric |
The transition structure was guessed by first drawing the product in Gaussview then removing the bonds that would be formed in the reaction to give the reactant. Different distances between the ethene and cis butadiene were trialled before a successful transition structure was calculated to give a distance of 2.12 Å. An opt+freq calculation was carried out using the TS Berny optimisation method. The frequency calculation showed a frequency at -956 cm-1 which corresponded to the vibration shown in the gif file, confirming a transition structure for the Diels Alder reaction. This appears to be synchronous and shows the reaction mechanism of the two molecules coming together, unlike the smallest positive frequency at 147 cm-1 which shows a rocking motion that could potentially result in asynchronous bond forming.
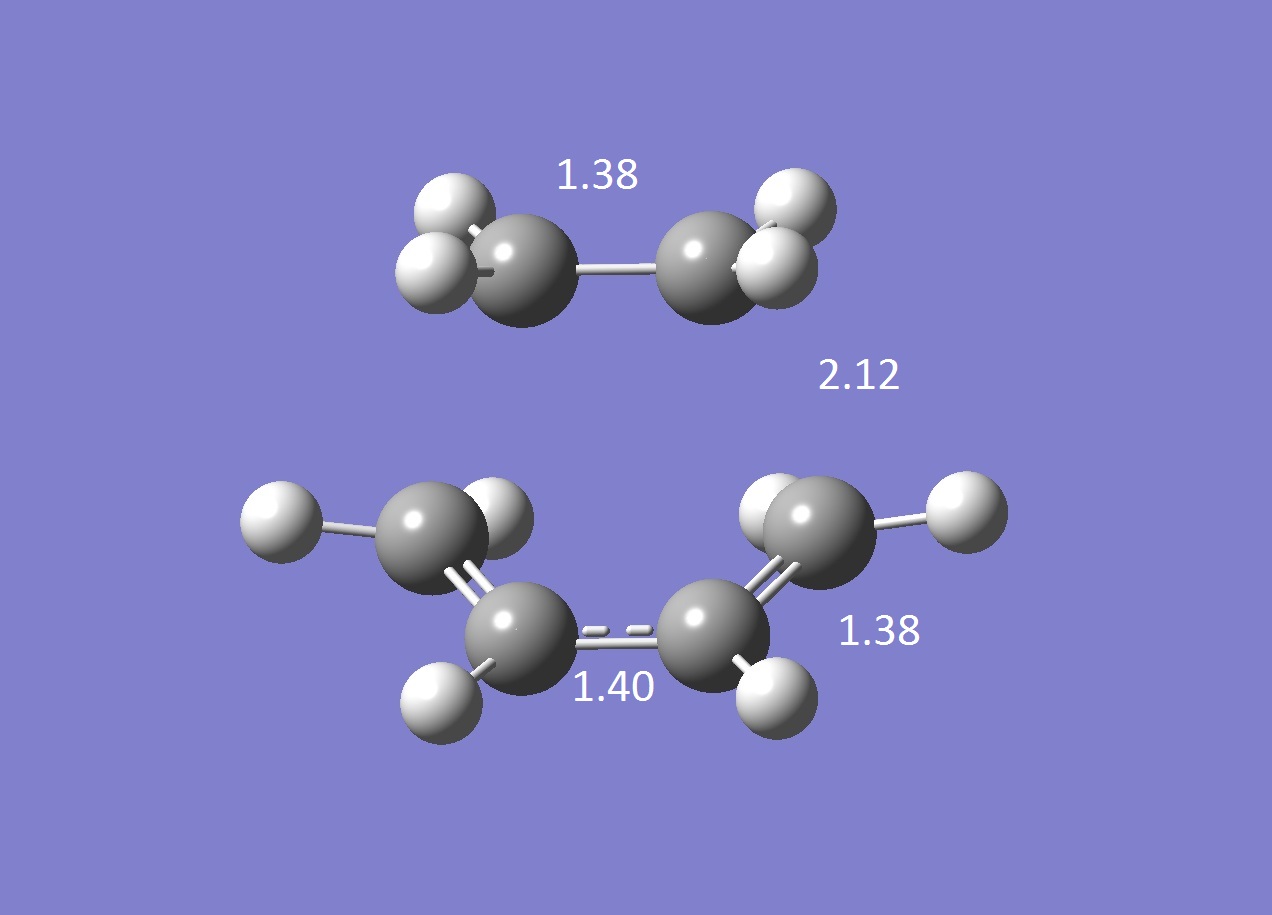
Typical sp3 and sp2 C-C bond lengths are 1.5 Å and 1.3 Å. The bond lengths are around 1.4 Å which are in between, indicating that the π bonds are lengthening to form σ bonds and the σ bond is shortening to form a π bond.
With a van der Waals radius of the C atom of 1.7 Å [3], the C-C bondlength of the partly formed C-C bond in the transition structure is much smaller than the sum of the two van der Waals radii but not small enough to be a C-C σ bond.
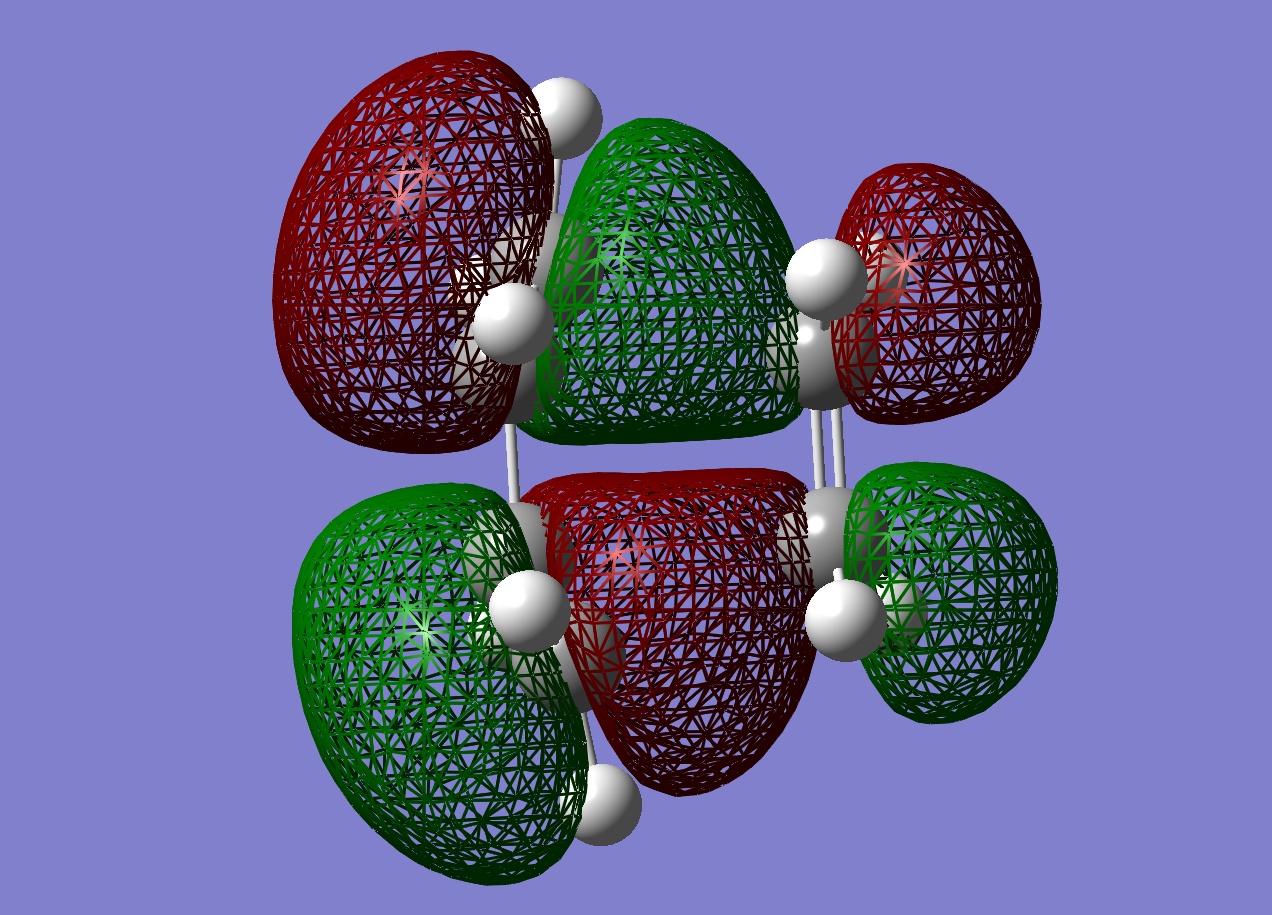
The HOMO was plotted and the HOMO is shown to be antisymmetric with respect to the plane. The HOMO involves the HOMO from butadiene and the LUMO from ethene. These molecular orbitals can interact because they are of the same symmetry (antisymmetric) and the mixing of these orbitals matches the shape of the HOMO.
File:DIELS ALDER BERNY TSV2.LOG
Regioselectivity of the Diels-Alder Reaction
In this section, the transition structure was investigated for the endo and exo adducts of cyclohexa-1,3-diene and maleic anhydride. The endo is the favoured product due to mainly kinetic control so the exo product is predicted to have the higher energy transition state.
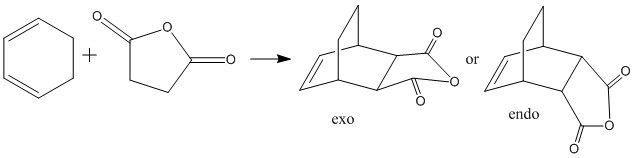
The energies were calculated to be very close for the two products - the energy was taken to be -31.6 kcalmol-1 for both though if more decimal places were considered, exo was slightly higher in energy as expected. The close match in energies suggests that one of the transition states has not reached its minima however further optimisations using the same TS Berny method on the AM1 theory of calculation did not give closer results. Although the bonds appeared to be the correct bond order in the checkpoint files, upon investigation of the bond lengths it was found that the endo form was in fact the exo form. Attempts were made to optimise the endo form but each optimisation yielded the exo form and limited time was available when the error was discovered.
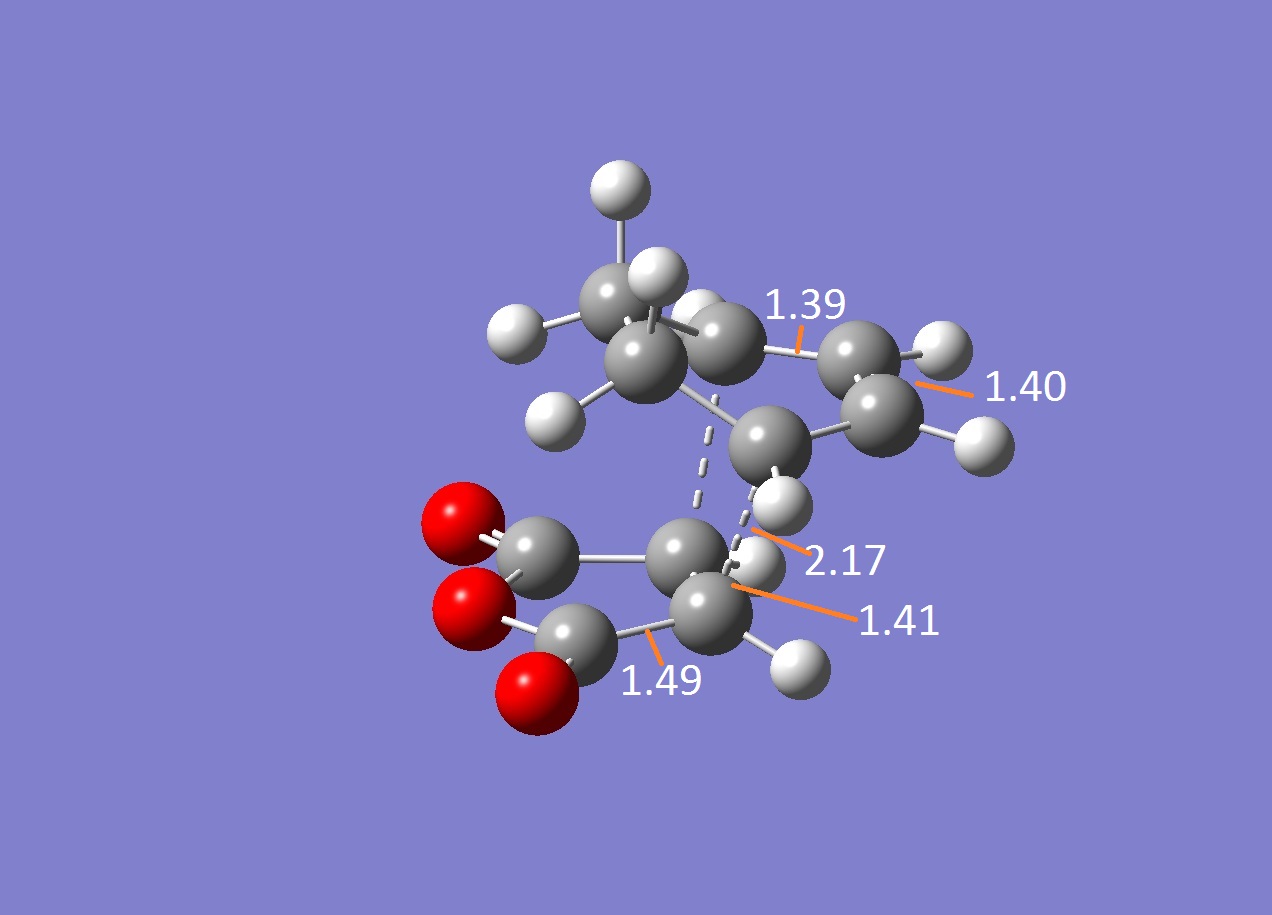
The bond lengths show the π bonds stretching to form σ bonds and the σ bond shortening to a π bond. The C-C bond forming distance between the two molecules is also shorter than the van der Waals radii to indicate the bond being formed. In the exo form, the distance between the (C)-O-(C) and the carbons opposite was 3.3 Å which is just slightly larger than the sum of their van der Waals radii (3.2 Å). A closer interaction would be sterically unfavourable.


The HOMO and LUMO were plotted which showed that both the molecular orbitals were antisymmetric. There was also a node between the -C(=O)-O-C(=O)- section and the rest of the molecule, indicating that this not part of the bond forming reaction pathway. If the endo had been successful, there may have been less of a separation between these molecular orbitals to favour the endo form over the exo form as a result of secondary molecular orbital interactions.
