Rep:Mod:khlmod1

Part 1: Hydrogenation of Cyclopentadiene

Part 1.1: Predicting the Geometry and Regioselectivity of the Dimerisation of the Cylcopentadiene Dimer

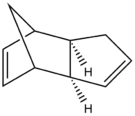
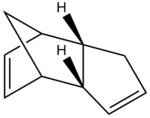
At room temperature cyclopentadiene dimerises by reacting with itself via a [4 + 2] Cycloaddition reaction. When cyclopentadiene dimerises it reacts via the Diels-alder reaction mechanism and can proceed to form either the exo or the endo dimer. The mechanisms for both outcomes are shown below .

Mechanism for the Formation of the Endo and Exo Dimer

Under thermodynamic control the exo product would be the dominant product (because it is thermodynamically favoured), however when under solely kinetic control the endo product would be the dominant product. If the exo product were found to be the most dominant product both thermodynamic and kinetic control could be operating on the reaction, and therefore one would be unable to conclusively determine whether the reaction is under solely thermodynamic or kinetic control.

Therefore to determine the most stable conformation of dicyclopentadiene, the endo and exo dimer were drawn in ChemBio 3D. Using molecular modeling (MM2 force field) the optimum stabilities of the molecules were calculated by optimising their geometries. This calculation yielded not only the total energy of each molecule but also calculated other energy interactions which all contribute to the total energy. These interactions include triatomic bond bends, diatomic bond stretches, tetra-atomic bond torsions, VDW energies and dipole-dipole interactions in each molecule. Molecular modeling using MM2 does not consider quantum mechanical factors and neglects to consider bond conjugation and molecular orbital effects which is a limitation of these calculations. Despite these limitations MM2 calculations do accurately determine VDW forces and optimise geometries, therefore ideally one would supplement MM2 with PM6, which accurately assesses hydrogen bonding and bond conjugation. The table below shows the results from the MM2 calculations carried out on product 1 (exo-dicyclopentadiene) and product 2 (endo-dicyclopentadiene).

Type of Energy Interactions	Product 1 (exo)	Product 2 (endo)	Difference in Energy between Exo and Endo Product
Stretch kcal/mol	1.286	1.250	0.0352
Bend kcal/mol	20.58	20.85	-0.2688
Stretch-Bend kcal/mol	-0.838	-0.8361	-0.0019
Torsion kcal/mol	7.656	9.511	-1.855
Non,1,4 VDW kcal/mol	-1.418	-1.545	0.1268
1,4 VDW kcal/mol	4.233	4.321	-0.0878
Dipole/Dipole kcal/mol	0.3775	0.4477	0.0702
Total kcal/mol	31.88	33.99	-2.121

The exo dimer displayed the lowest energy of the two products, with a total energy of 31.88 kcal/mol versus a total energy of 33.99 kcal/mol for the endo dimer. Therefore, the exo dimer is more stable than the endo dimer by 2.12 kcal/mol and therefore is the most energetically favorable dimer. Thus exo-dicyclopentadiene is the thermodynamic product and therefore is the dominant product when the reaction is under thermodynamic control.

Despite the exo dimer being more energetically favorable, the dimerisation of cyclopentaidiene selectively yields the endo isomer exclusively and therefore one can conclusively determine that the dimerisation of cyclopentadiene is under kinetic control since the kinetic product only is formed and therefore the stability of the product is determined by the relative stabilities of the transition state. it has been found that although the exo isomer is not directly formed during the dimerisation reaction near room temperature, recent studies in literature suggest that the exo isomer becomes more stable than the endo isomer above 200-250°C. furthermore, literature suggests that during thermal decomposition isomerisation between the endo dimer to the exo dimer occurs.

For each type of energy interaction the difference has been calculated between the two values calculated for each product (exo and endo). This enables one to directly compare the energy components of each molecule to help determine why the endo product is the preferred conformation and which energy interaction contributes the most to determine this outcome. From the table above one can see that the torsional energy calculated for the two molecules illustrates the greatest energy difference from the energy interactions observed in my calculations. The exo dimer has a lower torsional energy by 1.85 kcal/mol relative to the endo dimer. This shows that the hydrogens situated along the C-C bond formed as a result of dimerization are pushed closer together when the dimer is in the endo form than in the exo form. The closer the hydrogens are situated relative to each other the molceule as a whole becomes more strained, thus contributing to the higher total energy of the endo isomer. Therefore the torsional energy of the atoms placed in a 1,4 relationship contributes most to the total energy difference of 2.12 kcal/mol between the dimers.

Literature also suggests that in order to explain the occurence of the hindered endo dimer rather than the more stable exo dimer one needs to use moelcular orbital theory. Woodman, Hoffmann and Fukui first reported the favorable overlap of the p orbtials on the substituents of the dienophile with the p orbitals of the diene which they have concluded promotes the formation of the endo dimer. The diagram below illustrates this overlap in p orbitals which promotes a favorable interaction resulting in the endo dimer.

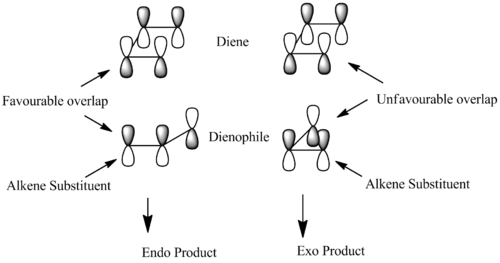
Part 1.2 The Geometry and Regioselectivity of the Hydrogenation of Cyclopentadiene Dimer

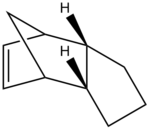
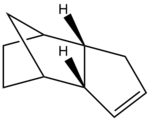
Furthermore, the endo-confirmation formed during the dimerisdation of cyclopentadiene undergoes hyrdogenation to form two hydrogenated dimers; Product 3 and Product 4. In order to determine the most energetically favourable comformation both products were again drwan in Chem Bio 3D and their geometries were optimised using molecular modelling (MM2 force-field) to obtain their relative stabilities. The results of these calculations are shown below.

Type of Energy Interactions	Product 3	Product 4	Difference in Energy between Product 3 and Product 4
Stretch kcal/mol	1.236	1.097	0.139
Bend kcal/mol	18.94	14.52	4.42
Stretch-Bend kcal/mol	-0.7610	-0.5494	-0.2116
Torsion kcal/mol	12.13	12.50	-0.3754
Non,1,4 VDW kcal/mol	-1.500	-1.070	-0.43
1,4 VDW kcal.mol	5.729	4.512	1.217
Dipole/Dipole kcal/mol	0.1631	0.1406	0.0225
Total kcal/mol	35.93	31.15	4.78

From these calculations one can see that when the endo conformation undergoes hydrogenation product 3 and product 4 are formed, of which product 4 is the most energetically favorable. Their relative stabilities were found to be 31.15 kcal/mol for product 4, and 35.93 kcal/mol for product 3. Therefore, product 3 was found to have the lowest overall energy and thus has the greatest relative stability.

The overall energy difference of 4.78 kcal/mol can be largely attributed to the bend energy interaction which differs by 4.42 kcal/mol (18.52 kcal/mol and 14.94 kcal/mol). This is supported further by the relative sp2 bond angles exhibited by product 3 (108°) and product 4 (112°). A typical C-C sp2 bond has a bond angle of 120° and therefore product 4 deviates less from the ideal bond angle and therefore one would expect it to be more favorable with less torsional strain. The calculations above however show that product 3 has a slightly lower torsional energy than product 4 (12.13 kcal/mol versus 12.50 kcal/mol). Despite product 4 displaying a slightly higher torsional energy than product 3, product 3 had a substantially larger bending energy (as previously discussed) and a larger 1,4 VDW interaction than product 4. Therefore the higher torsional energy exhibited by product 3 is overcome by the higher bending energy and 1,4 VDW interaction of product 4.

Despite the calculations above determining that the thermodynamic product is favorable one cannot conclude with certainty whether the reaction operates under thermodynamic or kinetic control. in order to conclusively determine whether the reaction is under thermodynamic or kinetic control one would have to look at the transition state within the hydrogenation reaction which is not possible with molecular modelling.

Part 2 : Sterochemistry and Reactivity of an Intermediate in the Synthesis of Taxol

Intermediate 9 of the Synthesis of Taxol (in the chair conformation)	Intermediate 10 of the Synthesis of Taxol (in the chair conformation)

In the overall synthesis of Taxol a key intermediate is formed this intermediate is either produced in the form of intermediate 9 or 10. These intermediates are an exmaple of atropisomerism. Atropisomerism arises when steric congestion restricts the free rotation about a single bond (in this case a sp²-sp² C-C bond), significanlty increasing the kinetic barrier for the rotation of bonds.

Therefore, in the case of taxol two sterioisomers are formed where the position of the carbonyl group is "fixed" either poiting up (intermediate 9) or down (intermediate 19). It has been suggested that on standing the compound apparently isomerises to the alternative carbonyl isomer. This implies that the kinetic product is formed first where subsequently isomerisation occurs to form the thermodynamic product.

The stereochemistry of carbonyl addition obviously depends on which isomer is the most stable and therefore intermediates 9 and 10 were again drawn out in Chem Bio 3D and their geometries were optimised using molecular modelling (MM2 force-field). The MMFF94 field was also used to calculate the overall energy to provide a comparison of the two techniques. On drawing intermediates 9 and 10 the structures were carefully considered to see whether any further minimisations could be achieved. The cyclohexane ring in both atropisomers can exist in different conformations. Of the various conformations possible for the six membered ring, including chair, twist boat, boat and half chair, the twist boat and the chair were found to be the only stable conformers, therefore each intermediate was drawn in both the chair (Intermediate 9 (chair) and Intermediate 10 (chair)) and twist boat conformation (Intermediate 9 (twist boat) and Intermediate 10 (twist boat)) and their overall energies were compared. The data obtained is shown in the table below.

Type of Energy Interactions		Stretch (kcal/mol)	Bend (kcal/mol)	Stretch-Bend (kcal/mol)	Torsion (kcal/mol)	Non,1,4 VDW (kcal/mol)	1,4 VDW (kcal/mol)	Dipole/Dipole (kcal/mol)	Total Energy (MM2) (kcal/mol)	Total Energy (MMFF94) (kcal/mol)
Intermediate 9 (Chair)		2.696	15.80	0.3271	19.49	-1.621	13.79	-1.751	48.74	67.89
Intermediate 9 (twist boat)		3.048	18.14	0.2066	20.54	-0.3065	15.05	-1.705	54.97	80.47
Intermediate 10 (chair)		2.469	12.39	0.2145	16.22	-2.005	12.44	-1.584	40.15	60.06
Intermediate 10 (twist boat)		2.900	15.74	0.4593	23.09	-1.753	14.98	-1.982	53.44	76.48

From the data above one can conclude that the six membered carbon ring in the chair conformation results in the most stable conformer. The overall energy of the twist boat conformations of both intermediate 9 and 10 are considerably higher than the chair conformation, 54.97 versus 48.74 kcal/mol and 53.44 kcal/mol versus 40.15 kcal/mol respectively. When analysing intermediate 9 the difference in energy between the chair and twist boat conformation can be mainly attributed to bend energy the stretch energy the torsional energy and the 1,4 VDW energy. The bend energy is increased in the twist boat conformation by 2.34 kcal/mol, while the torsional energy increases by 1.05 kcal/mol and the 1,4 VDW energy increases by 1.26 kcal/mol. Therefore when in the twist boat conformation a greater strain is imposed across the molecule and therefore the total energy is considerably higher. Similarly, for intermediate 10 the difference in overall energy between the twist boat and the chair conformations can be attributed to the bend energy, the torsional energy and the 1,4 VDW energy. In the case of intermediate 10 the torsional energy is significantly higher in the twist boat than the chair conformation, with an increase of 6.87 kcal/mol in the twist boat conformation. Therefore the increase in torsional energy contributes over 50% of the total energy difference between the two conformations. The 1,4 VDW energy does also increase by 2.54 kcal/mol and the bend energy also increases in by 3.35 kcal/mol on changing from the chair conformation to the twist boat conformation. Therefore one can decisively conclude that the twist boat conformation in both intermediate is too high in energy to exist in any considerable amount, as the literature also suggests.

Additionally, the calculations above also found intermediate 10 (in the chair conformation) to be the most stable intermediate with an overall energy of 40.15 kcal/mol for intermediate 10 versus an overall energy of 48.74 kcal/mol for intermediate 9. The difference in energy between the two intermediate of 8.59 kcal/mol is considerably contributed to by the increase in torsional energy, which increases by 3.27 kcal/mol between the two intermediates. However, in addition to this the bend energy and the 1,4 VDW interaction also contribute quite significantly to the energy gap, with an energy increase of 3.41 kcal/mol and 1.35 kcal/mol respectively. Therefore with a significant difference in energy intermediate 10 is the most generically stable intermediate and therefore one can conclude that it is the thermodynamic product

The energy difference exhibited by the two atropisomers can be attributed to the positioning of the carbonyl bond but also to the olefinic bond located adjacent to the olefin bridgehead. The steric strain imposed by an olefin bridgehead is a result of both the residual steric strain of the carbon skeleton and the extra strain imposed by the double bond. Therefore, one would assume that in order to reduce the overall steric strain of the molecule, the double bond would readily functionalise to form a new bond. However, the olefin bond is extremely reluctant to functionalise resulting in hyperstability of the molecule. Despite the additional strain imposed by the olefinic bond adjacent to the bridgehead the molecule exhibits less torsional strain than would be expected. To demonstrate the hyperstability of isomer 10 one can look at the saturated intermediate and compare the total energies and torsional energies of the two molecules. Both molecules were drawn out in ChemBio 3D and their energies were optimised.

Intermediate		Stretch Energy (kcal/mol)	Bend Energy (kcal/mol)	Stretch-Bend Energy (kcal/mol)	Torsion Energy (kcal/mol)	Non,1,4 VDW Energy (kcal/mol)	1,4 VDW Energy (kcal/mol)	Dipole/Dipole Energy (kcal/mol)	Total Energy (kcal/mol)
Intermediate 10 (Chair)		2.487	12.39	0.2145	16.22	-2.005	12.44	-1.584	40.15
Saturated Intermediate 10 (Chair)		2.994	13.41	0.4765	19.82	-1.009	14.74	-1.738	48.69

Therefore the calculations above illustrate that the saturated form of intermediate 10 has both a greater torsional energy (19.82 kcal/mol versus 16.22 kcal/mol) and a greater overall energy (48.69 kcal/mol versus 40.15 kcal/mol). Therefore the intermediate 10 is thermodynamically more favourable than its saturated counter-part. The difference in total energy of the two molecules is mainly increased by an increased torsional energy, which differs by 3.60 kcal/mol and an increase in 1,4 VDW energy, which differs by 2.30 kcal/mol. The torsional energy can be further explored by looking at the relative bond angles. In the saturated taxol intermediate the bond angle of the sp3 hybridised C-C-C is 121° which ideally should be 109.5°. Whereas the unsaturated taxol intermediate has a bond angle for the sp2 hybridised C=C-C of 125° which ideally should be 120°. Therefore the saturated taxol intermediate deviates further from the ideal bond angle and therefore the molecule experiences greater steric strain which increases the torsional energy and the overall energy of the molecule resulting in the unsaturated taxol intermediate being more thermodynamically favourable.

Part 3: Modelling Using Semi-Empirical Molecular Orbital Theory

3.1 Regioselective Addition of Dichlorocarbene

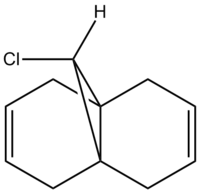
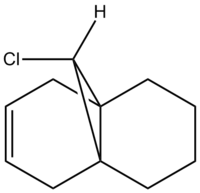
Compound 12 illustrates orbital control of reactivity when reacting with electrophilic reagents such as dichlorocarbene or peracid. In order to predict the geometry of molecule 12 while calculating the energy of the orbitals and illustrating their form graphically one uses ChemBio 3D. These calculations illustrate the transition from a classical mechanical treatment of a molecule to quantum mechanical treatment, which includes the wave-description of the electrons.

According to literature the regioisomeric addition of dichlorocarbene to compound 12 yields two major products; the dihydrated product whereby both double bonds syn and anti to the C-Cl bond are hydrogenated and a mono-hydrated product where only the double bond syn to the C-Cl bond is hydrated.

Addition of Dichlorocarbene

The major product (73%) is the mono-hydrated product and in order to explain this outcome one can analyse compound 12.Initially, compound 12 is drawn out in ChemBio 3D and its geometries optimised using the MM2 force-field. This neatens up the molecule and allows more precise calculations to be made.

Compound 12

Type of Energy Interactions	Stretch (kcal/mol)	Bend kcal/mol)	Stretch-Bend (kcal/mol)	Torsion (kcal/mol)	Non,1,4 VDW (kcal/mol)	1,4 VDW (kcal/mol)	Dipole/Dipole (kcal/mol)	Total Energy (MM2) (kcal/mol)
Compound 12	0.6191	4.73	0.0398	7.663	-1.065	5.795	0.1124	17.89

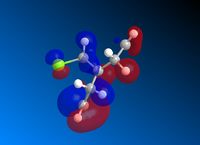
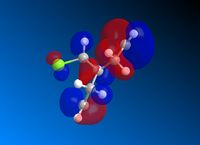
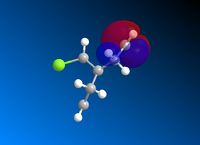
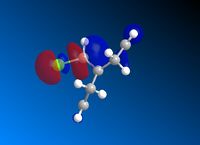
Following MM2 minimisation, MOPAC/PM6 force-field was used to calculate the energy of the molecular orbitals and obtain a graphical representation of the energy surfaces. The HOMO appears as default but it is also possible to view other molecular orbitals, therefore the HOMO, HOMO-1, and LUMO, LUMO + 1 and LUMO + 2 orbitals are modelled using this method. The graphical displays of the energies of the molecular orbitals are shown below using ChemBio 3D below where the blue areas represent negative regions and the red area represent positive regions.

HOMO	HOMO-1	LUMO	LUMO+1	LUMO+2

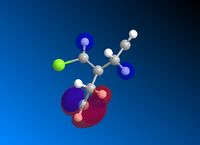From the MOPAC/PM6 calculations one can see that the HOMO displays a large proportion of electron density on the syn pi bond with very little electron density on the anti pi bond. This suggests that the HOMO is very susceptible to electrophilic attack. Conversely the LUMO illustrates that much of the molecular orbital energy can be found on the anti pi anti-bonding bond. This suggests that the LUMO is very susceptible to nucleophilic attack. Thus one can conclude that the electrophilic attack of compound attacks the syn pi bond whereas nucleophilic attack will target the anti pi bond (to the C-Cl bond). Therefore from these graphical representations of the molecular orbital energies of compound 12 one can see why the electrophilic addition of dichlorocarbene (dichlorocarbene is a strong electrophile) to compound 12 hydrates the olefinic bond syn to the C-Cl bond. Furthermore, on analysis of the HOMO-1 molecular orbital one can see that there is large propotion of electron density on the pi bond anti to the C-Cl bond. This suggests that attack by dichlorocarbene at the anti pi bond would be unfavourable due to the energy mismatch. The HOMO-1 is therefore to low in energy to interact favourably with most electrophiles. The stability of the olefin bond anti to the C-Cl bond is therefore particularly stabilised due to its overlap with the σ* anti-bonding C-Cl bond. This is due to the anti pi bond energy being close to that of the σ* anti-bonding C-Cl bond, since the electronegativity of the Cl atom lowers the energy of the σ* anti-bonding C-Cl bond sufficiently to allow it to interact. The stability of the anti pi bond is only lowered enough to react when the syn olefin bond has been hydrogenated. The syn olefin bond is not stabilised in the same way as the anti olefin bond due to its position and oritentation in the molecule.

Compound 12	Hydrogenated Compound 12

The vibrtaional frequencies of compound 12 and of its mono-hydrated product were explored, where the mono-hydrated product had the olefinic bond anti to the C-Cl bond removed. both molecules were drawn in ChemBio 3D and then their energies were optimised and frequencies calculated using Gaussian via the b31yp/6-31G(d,p) method.

Compound 12 IR	Hydrogenated Compound 12 IR

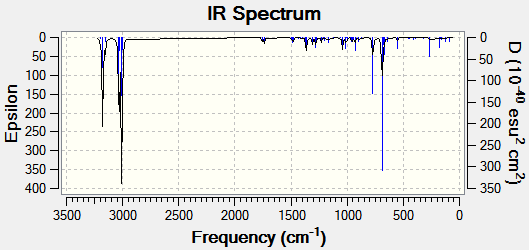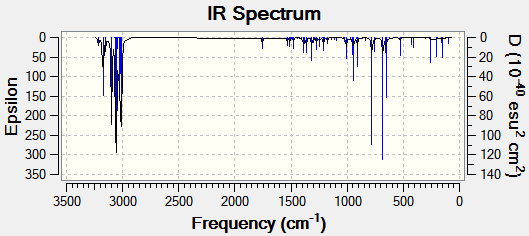Vibrational Spectra of Compound 12 publication : http://hdl.handle.net/10042/to-10388

Vibrational Spectra of Hydrogenated Compound 12 publication : http://hdl.handle.net/10042/to-10389

Compound		C=C Bond Stretch (Syn) (cm-1)	C=C Bond Stretch (Anti) (cm-1)	C-Cl Bond Stretch (cm-1)
'''Compound 12'''		1757.37	1737.12	770.91
'''Hydrogenated Compound 12'''		1753.76	n/a	779.93

The vibrational spectra were predicted using DFT. The data above shows that on remvoal of the olefinic bond the wavenumber of the C-Cl bond increases from 770.91 in compound 12 to 779.93 cm-1 in the mono-hydrated molecule. This suggests that when the olefinic bond is removed the C-Cl bond strength increase (becomes shorter). This can be explained by the absence of the anti C=C bond in the mono-hydrated molecule since the C-Cl σ* orbital overlaps with the anti C=C pi bond which then allows the donation of electron density into the C-Cl σ* orbital weakening the C-Cl bond.

3.2 Monosaccharide Chemistry: Glycosidation

Glycosidation involves the nucleophilic substitution of X for Nu. It is reported that glycosidation almost solely produced the 1,2-trans product where the Nu is int he equatorial positions trans to the OAc protecting group which is also in the equatorial position. the 1,2 trans product is known as the β anomer, while the less common α anomer is where the Nu takes up the axial position with the OAc protecting group cis in the axial position. The 1,2 trans product dominates glycosidation due the neighbouring group effect. The positioning of the OAc protecting group results in differing interaction with the oxonium ion on the ring and therefore produces two different possible products. when the OAc group is in the axial position and therefore attacks the oxonium ion from above the molecule, producing an intermediate oxonium ring that lies above the plane of the molecule, allowing nucleophilic attack below the plane of the molecule, thus producing the α anomer. Conversely when the OAc group is in the equatorial position it can attack the oxonium ion from below the plane of the molecule thus forming an oxonium ring intermediate pointing below the plane of the molecule promoting nucleophilic attack above the plane, resulting in the β anomer. Although typically glycosidation almost exclusively produces the β anomer , it is not always completely stereospecific. Therefore the possibility of other intermediates arises.

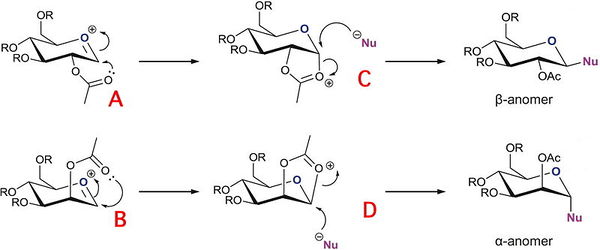
In order to effectively analyse the regioselective reaction of glycosidation the PM6 force field was used to calculate the overall energy as well as the MM2 force-field. The MM2 force field is usually a useful tool to use to initially minimise the energy of a system, however, in this case MM2 is ineffective in that it neglects to consider the neighbouring group effect. The neighbouring group effect is essential when considering the acetyl group and the oxonium ion. In addition the MM2 modelling technique does not take bond conjugation into account which is ineffective in the case of the glycosidation reaction which involves the acyl group which is highly conjugated, thus resulting in discrepancies.

Methyl was used for the R group when modelling the monosaccharides and their derivatives. Methyl was chosen because of its low electron count and its lack of opportunity to hydrogen bond. Methyl has a much lower electron count than an acetyl protecting group making the calculations easier and quicker. Additionally, methyl doesn’t have the opportunity to hydrogen bond unlike and OH group or such like, while having the advantages of behaving like an acyl group. Hydrogen bonding would again complicate the modelling procedure and make the calculations longer.

The data calculated above demonstrates the relative stabilities of A/A’, B/B’, C/C’, D/D’. In conformer A the OAc group is in the equatorial position (therefore pointing below the plane of the molecule). A/A’ therefore refers to the acyl group pointing below the plane of the molecule and the acyl group pointing above the plane respectively. B/B’ similarly refers to the B conformer where the OAc group is in the axial position (therefore pointing above the plane of the molecule) but B specifically refers to the Ac group pointing above the plane of the molecule and B’ pointing below the plane of the molecule. C and D represent conformers where the oxonium ring points below and above the plane of the molecule respectively. C’ and D’ refer to when the oxonium ring is in the plane of the molecule and where the D’ C-C=O bond is pointing below the plane of the molecule and the C’ C-C=O bond is pointing above the plane of the molecule.

Energy Interaction	Monosaccharide A	Monosacchairde A'	Monosacchairde B	Monosacchairde B'	Monosacchairde C	Monosacchairde C'	Monosacchairde D	Monosacchairde D'
Stretch (kcal/mol)	2.821	2.589	2.796	2.510	1.759	2.995	1.818	2.576
Bend (kcal/mol)	10.65	10.05	10.57	11.50	16.50	18.31	14.34	16.67
Stretch-Bend (kcal/mol)	0.9717	0.9516	1.005	0.9479	0.7396	0.9013	0.6037	0.7138
Torsion (kcal/mol)	1.679	5.086	3.943	1.769	7.705	9.655	7.812	6.811
Non,1,4 VDW (kcal/mol)	0.9935	-1.761	0.1818	-0.5667	-4.047	-2.669	-5.115	-2.812
1,4 VDW (kcal/mol)	18.725	19.734	19.298	18.486	17.437	19.297	18.646	19.268
Charge/Dipole (kcal/mol)	-19.91	-6.515	-19.34	-9.805	-4.906	0.6658	1.527	-0.5384
Dipole/Dipole (kcal/mol)	7.086	5.154	6.385	5.251	-0.9757	-0.8614	-0.2173	-0.8563
Total Energy (MM2) (kcal/mol)	23.02	35.29	24.84	30.19	34.22	48.29	39.41	41.83
Total Energy (PM6) (kcal/mol)	-89.24	-77.42	-88.52	-77.51	-91.66	-60.98	-90.51	-66.67
Positioning	Acyl group is positioned below the plane of the molecule	Acyl group is positioned above the plane of the molecule	Acyl group is positioned above the plane of the molecule	Acyl group is positioned below the plane of the molecule	Oxonium ring is positioned below the plane of the molecule	The double bonded oxygen in the oxonium ring points above the plane of the molecule	Oxonium ring is positoned above the plane of the molecule	The double bonded oxygen in the oxonium ring points below the plane of the molecule

The A conformer seems to be the most favourable when comparing the A/A’ conformers, with energies of 23.02 kcal/mol and 35.39 kcal/mol respectively (MM2). Both the MM2 calculations and PM6 calculations displayed the same trends. Additionally the B conformer appears the most favourable between the B/B’ conformers, with energies of 24.84 kcal/mol and 30.19 kcal/mol respectively. The differences in energy between A/A’ and B/B’ can be attributed to the differences in charge/dipole energies. When looking at the energy interaction that’s contribute to the total energy the charge/dipole interaction is the only energy interaction with a notable difference between conformers (other energy interactions have a discrepancy less than 1). Between A and A’ the difference in charge/dipole energy is 13.39 kcal/mol (-19.91 kcal/mol versus -6.5153 kcal/mol). When looking at the molecules it is evident that in the A’ and B’ conformers the polar oxygen on the acetyl group is orientated such that interaction with the oxygen on the ring is possible. This orientation of the polar oxygen atoms is less energetically favourable due to the electrostatic repulsion that occurs between them when they are able to interact.

When comparing the energies of the C/C’ and D/D’ conformers the calculations demonstrate that the C and D are more energetically favourable. Again, this can be related back to the charge/dipole energies as well as many other factors including in particular torsional energy. The instability of the C’ and D’ conformers is reflected by the increased strain exhibited when the oxonium bridgehead is in the trans position rather than in the cis as in C and D.

Click Chemistry Mini Project

It has been known for some time that the dipolar cycloaddition of organic azides and alkynes is the most direct route to 1,2,3-triazoles. However, this reaction route requires a high activation rate and progresses very slowly, often at very high temperatures and forms a mixture of regioisomers. This is obviously not ideal, and research has been undertaken to improve the conditions and rate of reaction but also to try and isolate particular regioisomers. This was first achieved when it was found that Cu could catalyse the reaction (thus lowering the activation rate) and selectively forms the 1,4-distributed 1,2,3-triazole under mild conditions. There are two possible regioisomers that can be formed when reacting substituted alkynes and substituted azides, either a 1,4-subsititued triazole (regioisomer A) or a 1,5-subsitiued triazole. Interestingly, it was later found that Ru could also catalyse this reaction but that Ru selectively produces the 1,5-subsitiued triazole (regioisomer B). by using different Ru complexes it is possible to form 100% of either regioisomer A or regioisomer B selectectively. For example, Ru(OAc)2(PPh3)2 exclusively yields regioisomer A, while Cp*RuCl(PPh3)2 and Cp*RuCl(NBD) exclusively yields regioisomer B.

The mechanism for the 1,3-dipolar cycloaddition between an azide and an alkyne to give a 1,2,3-triazole is shown below, with both regioisomers displayed. Both the azide and the alkyne are substituted and it was dictated that these R groups would be the literature which uses R1=Ph and R2=CH2Ph.

'Ru Catalysed Cycloaddition of Benzyl Azide and Phenylacetylene

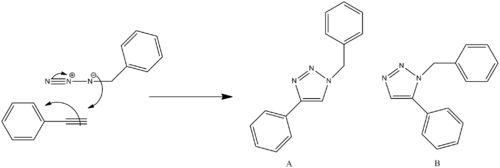
MM2 energy Optimisation

In order to distinguish which regioisomer is more energetically favourable MM2 force-field was used to optimised the geometry and minimise the energy and give an indication of differences, if any, of the energy interactions seen in both molecules. The data obtained is shown below.

Energy Interaction	Regioisomer A (kcal/mol)	Regioissomer B (kcal/mol)
Stretch	0.6416	1.239
Bend	10.308	16.05
Stretch-Bend	-0.0298	0.1965
Torsion	-15.79	-15.71
Non,1,4 VDW	-1.723	1.242
1,4 VDW	14.44	14.10
Dipole/Dipole	-0.6766	-0.8344
Total Energy (MM2)	7.164	16.283
Total Energy (PM6)	107.8	107.2

Regioisomer A after MM2 Minimisation	Regioisomer B after MM2 Minimisation
Jmol	Jmol

The MM2 force-field calculations illustrated that regioisomer A is more energetically favourable and is the thermodynamic product. By looking at the energy interactions, from a difference in total energy of 9.12 kcal/mol, 5.74 kcal/mol of this energy difference originates from the considerably higher bend energy of regioisomer B from regioisomer A. The bend energy increases from 10.308 kcal/mol in regioisomer A to 16.05 kcal/mol in regioisomer B.

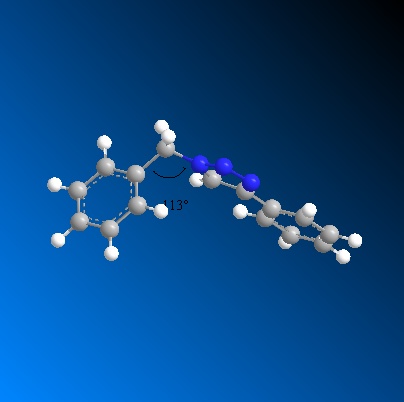
In the case of regioisomer A the benzyl ring 4-substituted to the triazole ring is in the plane of the molecule, i.e both the triazole ring and the benzyl ring are in plane with each other. However, the CH2Ph group 1-substituted the triazole ring displays a bend in the bridging carbon. The bridging carbon is 110° which is considerably close to the ideal bond angle of 109.5° for a sp3 C-C bond and therefore conformers to ideality to much greater extent that regioisomer B.

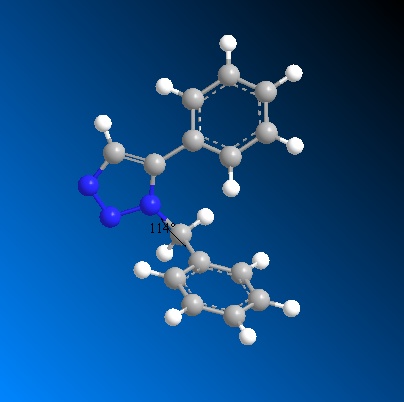
In the case of regioisomer B the benzyl ring 5-substituted to the triazole ring is in the plane of the molecule, i.e. both the triazole ring and the benzyl ring are in plane with each other. However, the CH2Ph group 1-substituted displays a considerable bend in the bridging carbon. The benzyl group is bent around the bridging carbon by an angle of 113° which does not conform with the theoretical bond angle of 109.5° for a sp3 C-C bond. This deviation from ideality indicates that there is some repulsion between the two benzyl rings when they are 1,5-substituted onto the triazole ring as opposed to 1,4-substituted.

Therefore with the added repulsion between the two benzyl rings when the triazole ring is 1,5-substituted, it is therefore higher in energy than its 1,5-substituted counterpart.

NMR Analysis

In order to calculate the NMR spectra for both molecules the energies and geometries of both molecules were further optimised using DFT calculations and submitting the regioisomers to scan. This was done using Gaussian mpw1psw91/6-31g(d,p). The Gaussian optimised regioisomers displayed slightly different bond angles. For the bend at the bridging carbon regioisomer A displayed a bond angle of 113° while regioisomer B displayed a bond angle of 114°. Thus, the DFT minimisation brought the two regioisomers bending energy slightly closer.

Regioisomer A after DFT Optimisation	Regioisomer B after DFT Optimisation
Jmol	Jmol

Regioisomeric Product	Total NMR	13C NMR (CDCl3)	1H NMR (CDCl3)
'''Isomer A'''	Isomer A	Total NMR of Isomer A	13C NMR of Isomer A	1H NMR of Isomer A
'''Isomer B'''	Isomer B	Total NMR of Isomer B	13C NMR of Isomer B	1H NMR of Isomer B

Optimisation of Isomer A in preparation for NMR publication: http://hdl.handle.net/10042/to-10392

Optimisation of Isomer B in preparation for NMR publication: http://hdl.handle.net/10042/to-10393

All NMR spectra analysed for isomer A in SCAN providing All elemnets NMR, 13C NMR, and 1H NMR when opened in Gaussian. Publication: http://hdl.handle.net/10042/to-10394

All NMR spectra analysed for isomer B in SCAN providing All elemnets NMR, 13C NMR, and 1H NMR when opened in Gaussian. Publication: http://hdl.handle.net/10042/to-10395

Regioisomer A NMR Analysis

Chemical Shif Value Calculated by Guassian (ppm)	Integral	Atom Assignation	Chemical Shift Value in Literature (ppm)	Discrepancy
144.85	1	2	148.0	+3.15
133.22	1	13	135.0	+1.78
127.72	1	6	129.5	+1.78
125.55	1	17	130.1	+3.45
125.21	1	11	129.5	+2.76
124.97	1	9	128.5	+1.03
124.81	2	15,16	128.0	+1.19
124.53	1	14	126.0	+1.47
124.24	1	18	126.0	+1.76
124.14	1	10	125.5	+1.36
121.88	1	12	125.5	+1.36
121.32	1	8	119.5	+1.82
116.98	1	3	119.5	+2.52
54.87	1	7	54.0	-0.87

Regioisomer B NMR Analysis

Chemical Shif Value Calculated by Guassian (ppm)	Integral	Atom Assignation	Chemical Shift Value in Literature (ppm) (No precise values available, only spectra)	Discrepancy
136.67	1	2	138.26	+1.33
134.10	1	13	135.66	+1.56
128.63	1	1	133.34	+4.71
126.23	1	8	129.64	+3.41
125.88	1	10	129.64	+3.76
125.61	1	9	129.08	+3.59
125.49	2	12,17	129.08	+3.73
125.19	1	15	128.92	+3.16
125.06	1	11	128.22	+2.52
124.70	1	6	127.22	+2.74
124.48	1	16	127.22	+3.26
123.67	1	18	126.93	+3.53
123.40	1	14	126.93	+3.25
52.24	1	7	51.85	-0.39

Using the GIAO approach the NMr spectra calculated computationally are relatively close to the literature values expected. The discrepancies between the literature and the calculations chemical shifts were relatively small, ranging from 0.39 to 3.76. This suggests that the NMR calculated was fairly accurate. One would expect that the main differences between the NMr of regioisomer A and the regioisomer of isomer B would be found in the 13C spectrum at the two carbons within the triazole ring. The difference between the two regioisomers is merely the position benzyl group is substituted onto the triazole ring, where it is either 4-substituted or 5-substituted onto the triazole ring. Interestingly, both regioisomers display the same trend. In regioisomer A C(2) and C(3) have chemical shifts of 144.85 ppm and 116.98 ppm respectively, where C(2) is bonded to the benzyl ring. Similarly in regioisomer B C(1) and C(2) have chemical shifts of 128.63 ppm and 136.67 ppm respectively, where C(2) is bonded to the benzyl ring. Therefore the carbon bonded to the benzyl group in both cases experiences less shielding and displays a greater downfield chemical shift (a higher ppm value). This is a trend one would expect to see since, the carbon bonded to the benzyl group is bonded to an electron withdrawing group which therefore takes electron density out of the system and therefore reduces its electronegativity. Therefore the aromaticity of the benzyl ring stabilises the carbon it is attached to and de-shields it, this results in the carbon atom having a greater downfield chemical shift, and thus it will have a lower ppm value. Therefore the NMr effectively differentiated the two different isomers by identifying which carbon was bonded the the benzyl group.

IR Analysis

Vibrational analysis was conducted to analyse the differences observed between the two regioisomers in order to support or contradict previous modelling techniques. Before submitting the regioisomers to SCAN to obtain the vibrational spectra of both molecules were minimised using MM2 force-field and MOPAC/PM6.

Isomer A IR

Isomer B IR

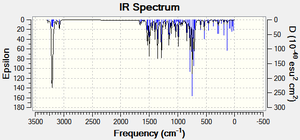
Vibrational analysis of Isomer A publication : http://hdl.handle.net/10042/to-10391

Vibrational analysis of Isomer B publication: http://hdl.handle.net/10042/to-10390

Vibration	Regioisomer A Wavenumber (cm-1)	Regioisomer B Wavenumber (cm-1)
C-H Stretch (Triazole)	3301.54	3275.88
C-H Bond Bend (CH2Ph Arene)	741.82	743.47
C-H Bond Bend (Ph Arene)	780.03	779.66
C-H Bond Stretch (CH2Ph Arene)	3210.92	3203.75
C-H Bond Stretch (Ph Arene)	3207.66	3201.25
N-N Bond Stretch (Triazole)	1304.05	1282.44
C=C Bond Stretch (CH2Ph Arene)	1660.03	1643.13
C=C Bond Stretch (Ph Arene)	1662.21	1633.06
CH2 Bond Stretch	3085.62	3076.38
CH2 Bond Bend	3137.75	3130.78

The IR data obtained above shows that the regioisomers differ very little when analysing different bonds wavenumbers. It is evident that the arene rings differ very little between regioisomers, although there seems to be a slight tendency for the wavenumber of the bonds to marginally increase between regioisomer B and A, with A generally slightly higher in wavenumbers. The differences in spectra which are particularly notable are the changes in the wavenumbers of the C-H triazole bond and the N-N triazole bond. This is exactly what one would expect to see, since essentially the only change seen between the regioisomers is the position of the benzyl group in the triazole, which is either 1,4-subsitiuted (regioisomer A) or 1,5-substituted (regioisomer B), therefore only having aeffect of the stability of the triazole ring. Interestingly, the C-H triazole bond wavenumber and the N-N triazole wavenumber both decrease between isomer A and B. Therefore, on changing from the 1,4-subsitiued triazole to the 1,5-substituted triazole the wavenumber of the N-N=N bond and C-H bond both increases suggesting that both bond strengths increase and the bond get shorter.

Conclusion

Optical rotation calculations were not used because there is not chiral centre is either regioisomers. However, further analysis could have been conducted by modelling an electronic circular dichroism. This said, the analysis done above was very effective in distinguishing between the two regioisomers. The errors produced by modelling the spectra were minor. To extend this mini project further I would look at a range of R’ groups rather than just the set discusses above and look for differences in energetic preferences for the substitution of the triazole ring and look at a wider range of possible isomers.

References

<References>