Rep:Mod:kga08module3wiki
Computational Exercise in Transition State Optimisation: by Keith Andrews
In this report, transition states for several pericyclic reactions are found, characterised and mapped onto the reactants and products on a potential energy surface. The methods applied are explained as the report progresses, and comparison to the literature made to evaluate the methods used.
- Firstly, the Cope Rearrangement is used as a tutorial in transition state optimisations, because the reactant and product are identical, which simplifies matters. The chair and boat transition states are contrasted and the mechanism described in terms of synchronicity. Different methods of obtaining an optimised transition state are investigated and temperature studies conducted to monitor the change of the various energies with temperature.
- The reaction of butadiene with ethylene is a standard and much studied Diels-Alder cycloaddition reaction computationally, due to its simplicity (only one product). The calculations here show how accurate the DFT B3LYP/6-31G* method is compared to the experimental data and secondary isotope effects are discussed as a means of determining the mechanism of a reaction.
- Finally, semi-empirical methods are used to optimise and explore the Diels-Alder reaction of maleic anhydride and 1,3-cyclohexadiene to investigate the endo effect. Secondary orbital interactions are evaluated and alternative arguments proposed. Solvent effects are investigated as a means of obtaining selectivity.
This program was used to handle journal references, and has been made available on the wiki for other users.
The Cope Rearrangement: Mechanistic Analysis
Outline
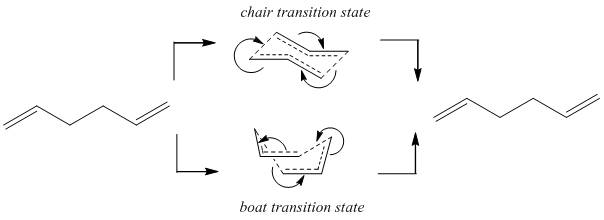
1,5-Hexadiene undergoes the Cope Rearrangement to form an identical "product". In order to discuss the mechanism of the reaction, the conformers of the molecule must be found. The mechanism is reported to go via an aromatic loose-chair transition state[1], implying a concerted/synchronous transition state. This is in agreement with the transition states found here using HF and DFT level calculations.
Optimisation of 1,5-Hexadiene
Experimental
1,5-hexadiene was drawn in Gaussview 5 in an antiperiplanar conformation. The structure was cleaned using the option in the edit menu and then optimised at the HF/3-21g level. This is a low level optimisation to get rough minima structures.
1,5-hexadiene was drawn again in Gaussview 5 in this time in a gauche conformation. The structure was cleaned using the option in the edit menu and then optimised at the HF/3-21g level again.
Whilst this method seems applicable to find a couple of the basic minima of the conformational energy surface of 1,5-hexadiene, a faster and more logical way of cataloguing the various minima is using molecular mechanics. 1,5-hexadiene was built in ChemBio3D and the linear conformation found, the most sensible to use as a standard orientation. One bond at a time, the dihedral driver utility was employed to rotate about each of the pertinent carbon-carbon bonds. At this point the terminal carbons can be thought of as R groups, which leaves three C-C bonds to optimise. Between each dihedral rotation, MM2 was used to tighten the structure slightly.
There are three sensible, non-eclipsed orientations per bond, and of course the permutations. Due to the symmetry of the molecule, only some of these minima are unique, and ~half the permutations are "atropisomers" - structures that are interconvertible via rotation of bonds, but whose minima are at identical energies (in this case).
Each of the MM2 optimised structures was imported into Gaussview and optimised at the HF/3-21g level using the Opt + Freq keywords. The frequency test ensures the found structure is a minimum on the potential energy surface; it also allows low frequency vibrations to be observed. It is found that the lowest energy vibrations, generally between 60 and 120 cm-1 (active at room temperature), resemble what would be a freely interconverting structures, rotating about the central C-C bond.
It is important to have an energy surface map so the transition state can be located. The symmetry of the molecule here is beneficial, as the product and the reactant are identical, and hence map to the same energy surface. Chair transition states are common transition states for cyclic organic reactions that can access such a geometry, as they mimic the most stable conformer of cyclohexane, so this is a good place to start searching for a transition state; where a chair is possible, a boat is also normally possible, so this must be tested too to ensure it is not a lower energy.
There are a number of ways that the transition state can be found and tested and these will be explored for this problem.
Analysis of the Hexadiene Optimisations
The energies and symmetries were extracted from the checkpoint files outputted Gaussian.
| Conformer | Energy/Eh | (Rel) Energy Difference kcal/mol |
| Anti 1 (C2) | -231.693 | 0.037 |
| Anti 2 (Ci) | -231.693 | 0.079 |
| Anti 3 (C2h) | -231.689 | 2.253 |
| Anti 4 (C1) | -231.691 | 1.061 |
| Gauche 1 (C2) | -231.688 | 3.103 |
| Gauche 2 (C2) | -231.692 | 0.624 |
| Gauche 3 (C1) | -231.693 | 0.000 |
| Gauche 4 (C2) | -231.692 | 0.710 |
| Gauche 5 (C1) | -231.690 | 1.911 |
| Gauche 6 (C1) | -231.689 | 2.197 |

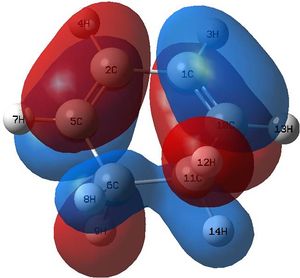
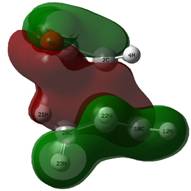
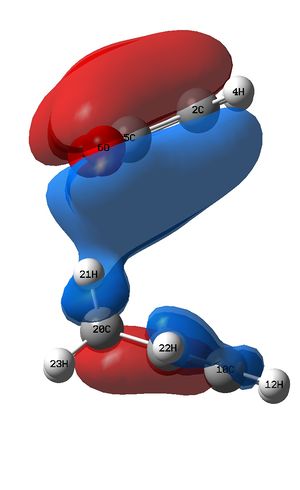
It is perhaps surprising that the lowest energy conformer here is the gauche 3 conformer. This may be a result of the low level calculation employed. The three lowest energy conformers, anti 1, 2 and gauche 3 were recalculated at the DFT B3LYP/6-31G* level (OPT/FREQ) and at this level of theory, the lowest energy structure is an anti-periplanar structure, with very little energy between the two anti-periplanar structures. The gauche, whilst still low, is clearly less favourable now, but still has a low energy, certainly compared to the other gauche systems. Looking at the molecular orbitals for this structure, perhaps the п-п interaction shown right helps stabilise the molecule. It was noted that the DFT optimised structures seemed tighter, but not significantly different to the HF level structures. They were cleaner versions of the same structure. This shows the viability of using low level calculations to map the basic potential energy surface, but not perhaps for calculations to compare the activation energy to the literature for example.
| Energy/Eh | Relative Values (kcal/mol) | |
| Anti 1 (C2) | -234.612 | 0.000 |
| Anti 2 (Ci) | -234.612 | 0.050 |
| Gauche 3 (C1) | -234.611 | 0.289 |
This exercise is purely to obtain the minima this molecule can conform to, so that when the IRC (intrinsic reaction coordinate) calculations are performed, a conclusive result can be reached (check the TS maps onto a real conformer of the product).
The frequency analysis characterises the critical point. By ensuring no imaginary frequencies (negative eigenvalues) were observed, a minimum can be confidently assigned (as the structure was successfully optimised to a stationary point). From the Thermochemistry data in the Gaussian output, the following was extracted for the anti-2 structure.
Sum of electronic and zero-point Energies= -234.469211 -:- potential energy at 0 K (zero-point vibrational energy E= Eelec + ZPE)
Sum of electronic and thermal Energies= -234.461854 -:- energy at 298.15 K and 1 atm; E = E + Evib + Erot + Etrans
Sum of electronic and thermal Enthalpies= -234.460910 -:- additional correction for RT (H = E + RT)
Sum of electronic and thermal Free Energies= -234.500825 -:- includes the entropic contribution to the free energy (G = H - TS)
The correct term must be used to compare to experimental values. The frequency analysis was re-run at 0 K to investigate the change in the corrections to the energies with temperature; this is reported later.
Optimising Transition States
Optimising the Chair Transition State for the Cope Rearrangement
Now a map of the energy surface had been found (in terms of pinpointing the minima), the transition states for the reaction could be worked on. Guessing the chair and the boat transition states is a good working hypothesis, but in order to lend any weight to the argument, evidence must be found that they map onto the energy surface of both the reactant and the product. If the transition state cannot link these two structures together, it is clearly not a transition state for the reaction. Several approaches were examined.
An allyl group was drawn, as shown right, and was optimised at the basic HF/3-21g level. A duplicate was made of the optimised structure, and positioned as shown, in the chair transition state-type orientation, with the two carbon sets that join in the reaction each 2.17 Å apart. There are then two methods to optimise the transition state.
1. These structures together were run using the following keywords:
opt=(calcfc,ts,noeigen) freq hf/3-21g geom=connectivity
This tells Gaussian to calculate the Force Constants once, to "minimise" the structure to a transition state (Berny). NoEigen acts to prevent the program from declaring failure if two imaginary frequencies are found - a transition state must only have one degree of freedom which lowers the energy upon exercising that mode - the reaction coordinate geometry change itself.
The optimisation leads to this structure: : which has an imaginary vibration at -818 cm-1. Animating this frequency shows the expected Cope Rearrangement reaction coordinate. Optimising at the DFT B3LYP/6-31G* level changes this vibration frequency to -566 cm-1.
2. The second method freezes the forming bonds and instead minimises the rest of the molecule (freezes the reaction coordinate, and minimises all other degrees of freedom). This may be useful in by-passing force constant calculation, which can be computationally expensive, as this method may allow a reasonable guess of the force constant matrix. It also helps filter out other possible imaginary frequencies that should not be observed in a true transition state.
For this method, the two adjoining carbon bonds were fixed at 2.20 Å and frozen. The rest of the structure was optimised to a minimum at the HF/3-21g level. : This resembles the expected state as calculated in the first method, but with longer bonds. Now the bonds are unfrozen, and optimised (to the correct length) to a transition state as before, but without the force constants option (this is the benefit of this method). The optimisation was successful, with the key outputs for each method identical; -818 cm-1 for the imaginary frequency, -231.619 Eh for the energy and 2.02 Å for the C-C bond lengths.
QST2 Method for Optimising the Boat Transition State
Whilst the previous method focused on finding a maximum point on the potential energy surface starting at a good guess, with one negative frequency indicating the second derivative was a maximum, this method interpolates between two minima. In this case it is fairly simple, as there should be symmetric minima about the transition state (the reactants and products are identical!). Therefore, building the reactant and duplicating it will suffice.
This is what was done; the one caveat is that the atom labels must also be changed, so that the reactant labels map onto the product labels via the reaction, and hence via the transition state. This is more obvious when the reactants and products are different.
Once the two structures are defined, the following keywords are supplied to Gaussian:
opt=qst2 freq hf/3-21g geom=connectivity
This tells Gaussian to optimise, in the HF/3-21g method and basis set, to a transition state by interpolating the two provided structures. It then applies the frequency analysis to confirm this is a maximum (transition state).
The anti2 structure of the hexadiene was optimised using the QST2 method and the structure returned from this resembles the chair transition state, but with the connectivity incorrect, as shown right. The original structure is far too loose to expect the convergence to do what is wanted. In order to find the transition state, a reasonable guess of what it looks like is required. Its structure is well recognised so adulterating the initial optimised structure to more resemble the expected boat transition state was fairly facile: the pre-optimised structures are shown below.

These structures did convergence to the desired boat transition state, with a slightly more negative force constant than for the chair .
Intrinsic Reaction Coordinate: Linking the Reactant and Product to Each Other Via the Transition State
It is plausible to suggest that the chair transition state would originate from the gauche 2 conformer, as this appears to have relatively little movement about the central C-C bond required to get from one to the other. Likewise, gauche 3 could rotate slightly about the central C-C bond to take the basic form of the boat transition state. However, this is not concrete evidence, as the visual pathway may not be a low energy pathway. To prove these structures do indeed link directly to the relative transition state via a low energy pathway, IRC calculations can be used.
IRC works by taking the imaginary frequency, and extrapolating along that mode, as this mode decreases the energy of the structure. (A transition state has one imaginary frequency, which means the structure lies on a maximum (saddle point), and can lower its energy by following the (only) negative curvature (the second derivative calculates the change in the gradient; negative means a maximum)). The IRC allows the molecule to optimise, whilst locking the negative mode, so it retains this mode as it optimises. The initial force constant calculation allows the calculation to "learn" the slope of the minimisation, and extrapolates down the degree of freedom allowing it to minimise its energy.
IRC for the Chair TS
The chair transition state was subjected to this calculation.
# irc=(forward,maxpoints=50,calcfc) rhf/3-21g geom=connectivity
The forward tells the program to only calculate down one side of the slope (in this case, the slope is symmetrical as the product and reactant are identical - in a normal reaction, where the product and reactant are different, both ways must be calculated to obtain both the structures the TS links to). The calcfc asks the program to calculate the force constants once, initially. This can lead to errors later on, if the guessed Hessian is a long way from what it should be. Maxpoints=50 gives the program fifty guesses to get to the real minimum. Also internally specified, but currently set to the default setting is stepsize=10, which is the change along the reaction coordinate imposed by each step of the calculation.

The optimisation seemed to be running successfully, based on the shape of the graph (right, below). However, the fiftieth step was reached without full convergence - the graph does not level off. At this point, however, the geometry already maps onto a plausible product structure, and a normal optimisation, as if the present structure has been guessed as a minimum, can be run to obtain a low energy structure. So the last structure from the IRC analysis was optimised, and the gauche 2 structure was found, with all properties identical to the predetermined data from above. This was an acceptable solution here, as the structure already mostly resembled the gauche 2 structure (the connectivity has assembled correctly), and the danger of falling into an incorrect minimum was low. The main errors that can occur here involve creating the incorrect bonds, but once these bonds are mostly formed, the connectivity cannot change, and the correct minimum can be reached. A second error might be the convergence to the wrong conformer, but this is less troublesome.
Other procedures are possible for this outcome. Firstly, the number of steps can be increased to allow the IRC to find the minimum. The number of steps was increased to 200, but Gaussian stopped after 51. Due to the step size guess, it is possible to "jump" over the minimum and get caught in an oscillating loop where the minimum is missed, but the stepsize is too big to converge into it.
Item Value Threshold Pt 50 Converged?
Maximum Force 0.000566 0.000450 NO
RMS Force 0.000143 0.000300 YES
Maximum Displacement 0.001225 0.001800 YES
RMS Displacement 0.000287 0.001200 YES
Predicted change in energy=-1.140005D-07
Optimization stopped.
-- Number of steps exceeded, NStep= 58
-- Flag reset to prevent archiving.
----------------------------
! Non-Optimized Parameters !
! (Angstroms and Degrees) !
---------------------- ----------------------
! Name Value Derivative information (Atomic Units) !
------------------------------------------------------------------------
This part of the log file states that the number of steps allowed within a point for converging the other modes has been exceeded. In other words, for the given geometry change along the reaction co-ordinate, the non frozen degrees of freedom could not be converged. This could be because the force constants were not calculated at every step, so the last step produced a structure too far from the real path, leading to a bad geometry. This is the main caveat with increasing the number of steps; the error in the Hessian is compounded and convergence can often fail.
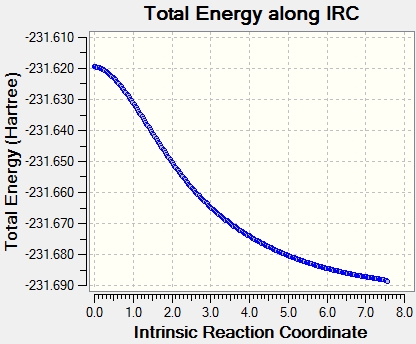
Further attempts were documented:
| Points | Stepsize | Energy/Eh | C-C Distance/A | |
| Attempt 1 | 50 | 5 | -231.659 | 1.66 |
| Attempt 2 | 350 | 5 | -231.687 | 1.56 |
| Attempt 3 | 350 | 3 | -231.689 | 1.56 |
| Gauche 2 | - | - | -231.692 | 1.55 |
Tightening the criteria allowed the result to converge to within error to the Gauche 2 structure. These improvements all amount to a more computationally expensive approach, none less so than another option; calculating the force constants on every point. This allows the gradient to be considered, and hence the next development to be better planned.
# irc=(forward,maxpoints=50,calcall) rhf/3-21g geom=connectivity
"calcall" tells Gaussian to calculate the force constants at every point. This optimisation was successful for only 50 points with no change in stepsize, giving an energy of -231.687, within the threshold for the minimum energy of the Gauche 2 conformer. The final structure can be tightened if desired by optimising normally.
IRC for the Boat TS
Calculating the IRC for the boat proved trickier. The structure was subjected to a basic IRC run thus:
# irc=(maxpoints=50,calcfc) rhf/3-21g geom=connectivity
The structure minimised to the following structure:

This structure is symmetrical, and corresponds to a maximum on the energy surface, when considering the conformational analysis and rotation around the central carbon carbon bonds. The calculation seems to have got stuck here, presumably as the structure is a stationary point, even though not a minimum. If indeed this structure is required to reach the transition state, the boat TS is predicted to be a lot higher in energy than the chair TS. (OPT and FREQ files)
Even from this structure, no optimisation was possible that led to minima, even when force constants were set to be calculated always. A frequency analysis showed one negative vibration, indicating that this itself is a transition point - the vibration is shown below, and corresponds to rotation around the same C-C bond.

Using the manual displacement possible with the vibration, the structure was made antisymmetric slightly, and the IRC continued, now finding the gauche 3 structure, as predicted initially. The same was tried with the initial structure, but unsurprisingly, the IRC became stuck at the same symmetrical structure.
Because a transition point was found rather than a minimum, an IRC was run from the stuck maximum, as shown in the picture. This managed to "un-stick" itself, and converged to an energy of -231.687 Eh. This structure was then optimised normally and again got to Gauche 3, with an energy of -231.693 Eh.
Although the IRC seems less than elegant at reaching the product, the same product is reached no matter which method is tried, both for the boat and the chair, so is a very useful way of linking the transition state to the reactant and product conformers/isomers.
Activation Energy
The energies of the transition states are shown below, showing that the chair transition state is a lower energy structure, with shorter C-C bonds; this implies the two fragments can approach each other better without unfavourable non-bonding interactions, but with better favourable interactions (the new C-C bonds are better formed in the chair TS, meaning a more stable structure due to better orbital overlap).
| HF/3-21g | DFT B3LYP/6-31G* | |||||||
| Symmetry | (Electronic and) Thermal Energy / Eh | Forming Bond C-C Distance / Å | Activation Energy (kcal/mol) | DFT (Electronic and) Thermal Energy / Eh | Forming Bond C-C Distance / Å | Activation Energy (kcal/mol) | Lit[2] (kcal/mol) | |
| Chair TS | C2h | -231.461 | 2.02 | 44.74 | -234.409 | 1.97 | 33.23 | 33.5 ± 0.5 |
| Boat TS | C2v | -231.445 | 2.14 | 54.81 | -234.396 | 2.21 | 41.39 | 44.7 ± 2.0 |
The activation energies are calculated from the thermal energies for comparison with the literature[2] which are in excellent accordance with the results from the DFT level calculations. The HF level calculations are clearly off the mark. The HF level activation energies were calculated from the lowest energy conformer in that method, gauche 3, and the DFT were calculated from anti 1, the lowest energy conformer as calculated above.
The chair transition state is hence shown to have a lower activation energy than the boat TS for this reaction, by 8.2 kcal/mol (DFT).
Energy Calculations at Other Temperatures
Using the following keywords, and minor editing to the input file, the energies were calculated for a variety of temperatures: (Note, that for the 0K run, 0.0001K was specified:
- 0K DOI:10042/to-8114
- 100K DOI:10042/to-8115
- 200K DOI:10042/to-8116
- 300K DOI:10042/to-8117
- 400K DOI:10042/to-8118
- 750K DOI:10042/to-8119
- 1000K DOI:10042/to-8120
- 10000K DOI:10042/to-8121
# freq=readisotopes rb3lyp/6-31g(d) geom=connectivity
The following was examined in the log file.
------------------- - Thermochemistry - ------------------- Temperature 0.000 Kelvin. Pressure 1.00000 Atm. Atom 1 has atomic number 6 and mass 12.00000 Atom 2 has atomic number 6 and mass 12.00000
Sum of electronic and zero-point Energies= -234.469211 Sum of electronic and thermal Energies= -234.469211 Sum of electronic and thermal Enthalpies= -234.469211 Sum of electronic and thermal Free Energies= -234.469211
The following is a summary of the data.
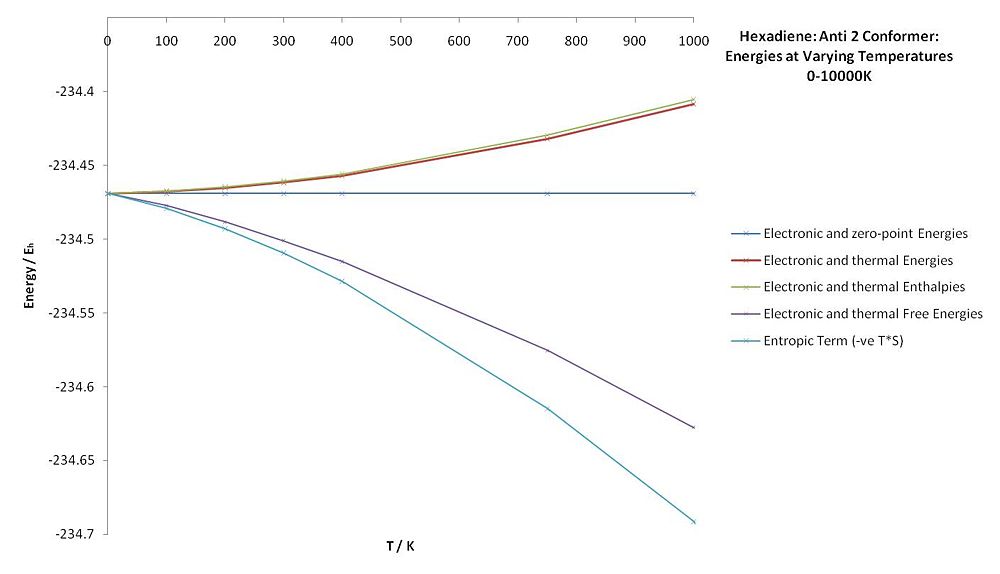
The electronic and zero-point energies do not change with temperature, as the molecule will be in the electronic ground state for all of the covered temperatures. The vibrational and rotational contributions to the thermal energies increase with temperature, but the free energy decreases. As the number of degrees of freedom increases (with the rotational and vibrational degrees of freedom), the overall free energy decreases as a function of temperature: ΔG = ΔH - TΔS. For the 0 K calculation, all types of energy are equal to the zero point energy, which is expected as no rotational, vibrational, translational or electronic levels will be excited.
Conclusions
- The minimum energy conformers were quickly catalogued using MM2.
- The HF method was used to calculate approximate ground state wavefunctions and a rough relative energy compared to the other conformers. At this level of theory, the gauche 3 was the most stable conformer, explained crudely by looking at the MOs.
- DFT level calculations concluded that the anti 1 and anti 2 conformers were the first and second lowest energy conformers respectively.
- The chair and boat transition states were found using several techniques:
- "Optimise to a Berny TS" optimised to a transition state given a good guess of what it is, minimising along all degrees of freedom except the reaction coordinate; this is roughly equivalent to guessing a minimum and optimising to a minimum.
- The Opt=ModRedundant freezes out specified criteria; in this case bond lengths were frozen. This locked the four reacting carbons into position, and allowed the rest of the molecule to be optimised to reduce chance of two imaginary frequencies being found. The resulting structure can then be optimised along the specified bonds that are breaking/forming (~ the reaction coordinate) without the need for calculating the force constant matrix.
- The QST2 method interpolates between the reactant and product to give a transition state; a good guess must still be made for this to work; this can alternatively be specified separately in a third input (QST3).
- The Intrinsic Reaction Coordinate calculation was utilised to prove the found TS/s mapped onto conformers of the reactants and products, and indeed which structures/conformers they were.
- All structures were refined at the DFT level and the activation energies found. It was concluded that the chair TS does map the reactants on to the products, and is 10 kcal/mol lower in energy than the boat TS in the HF level, and 8.2 kcal/mol lower in energy than the boat in the DFT level.
- The various energies of the anti 2 conformer of 1,3-hexadiene were calculated at various temperatures. As expected, the entropy increases with temperature (more degrees of freedom "unlocked"), decreasing the overall free energy by more than the increasing enthalpy contribution increases the free energy.
Computational Approach to the Diels-Alder Reaction
Outline: Reaction of Butadiene with Ethylene
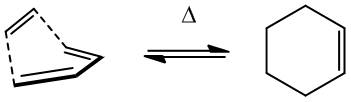
The s-cis- conformer of butadiene undergoes a Diels-Alder reaction with ethylene to give cyclohexene. The transition state was found using AM1 semi-empirical calculations, and thermochemical data extracted at the DFT B3LYP/6-31G* level.
Experimental: Butadiene and Ethylene
Cis- butadiene was optimised at the semi-empirical AM1 level in Gaussian. The structure appeared planar, and the frequency analysis showed one imaginary frequency. The structure was optimised again at the HF/3-21g level and the structure was observed to be different (non-planar). There were no imaginary frequencies in the vibrational analysis. The AM1 level calculation has only one STO and becomes stuck at the planar (eclipsed) maximum. Manually displacing the structure along the imaginary displacement and re-optimising leads to a minimum (no imaginary frequencies), slightly non-planar structure. The summary of the calculations are below.
Frontier Orbitals of the Fragments
The HOMO and LUMO of the optimised (AM1) structure were examined. The orbitals of ethylene are well known, with no nodes in the HOMO and one node in the LUMO, but are reproduced here for consistency.
The matched orbitals are outlined in the table and it is apparent that symmetry restricts the possible combinations to the HOMO-LUMO of each set.
Locating the Transition State of the Reaction
The planar butadiene structure from the AM1 calculation was positioned next to an ethylene molecule in the same drawing, and some parameters specified.
An unsuccessful route:

A unsuccessful route: the starting distances between the fragments was too small and similar to the product; the result was just cyclohexene; it was therefore decided to increase the inter carbon distance between the ethylene and the butadiene. The new sp3 nature of the product was guessed to by angling the "attack" to 109.5o. This was successful.
A successful route:

The AM1 routes used the following keywords:
# opt=(calcfc,ts,noeigen) freq am1 geom=connectivity
and the DFT route was at the following level:
# opt=(calcfc,ts) freq rb3lyp/6-31g(d) geom=connectivity
The transition state seemed plausible, and secondly there was one imaginary frequency that seemed to be following the reaction coordinate expected which shows a synchronous/concerted reaction pathway. The lowest real frequency appears to show the two fragments twisting apart. This cannot be a bond forming process as such because the two fragments do not approach each other, they are just rotating . The second lowest real frequency could well be an attempt at asynchronous bond formation .
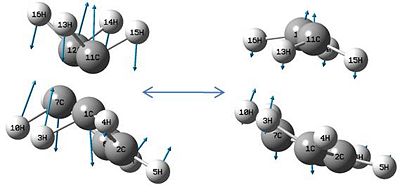
The geometry of the transition state can be rationalised: the vdW radius of carbon is reported to be 1.7 Å[3], with a more recent computational value for the carbon central to tert-pentane being 1.68 Å [4] Therefore, non-bonding carbon atoms become repulsive at about 3.4 Å (twice that radius). An sp3-sp2 carbon-carbon bond length in propylene is reported to be about 1.50 Å[5]. The value found in the transition state of 2.28 Å (lit. [6] 2.273 Å) is a distance smaller than the repulsive 3.4 Å just quoted for the vdW radius. Therefore it is implicit a bond is being formed between these two carbon atoms - the distance is much too long to be considered a full bond. Further, the bond length of the two non-reacting carbon atoms is found to be 1.41 Å in the transition state, shorter than the 1.50 Å quoted for a single bond of this nature, indicative that this bond is shortening (becoming a double bond).
The literature[7] values for these bonds are 2.2-2.3 Å for the forming bonds (here 2.28 Å), 1.39 Å for the forming double bond (here 1.41 Å) and 1.37 Å for the diene double bonds which become single bonds (here 1.38 Å), so the values are in good agreement with the literature.
IRC Analysis of the Transition State for the Reaction of Butadiene with Ethylene
To test the transition state is linked to the two structures, an IRC analysis was performed on the transition state. The following keywords were used, doing the forward and the reverse paths separately:
# irc=(forward,maxpoints=100,calcall) ram1 geom=connectivity
# irc=(reverse,maxpoints=100,calcall) ram1 geom=connectivity
It was decided to use the full force constant calculations given the trouble encountered without using them in the first section of this report. The IRC seemed to work flawlessly on this occasion, producing the cyclohexene for the forwards IRC, which had identical particulars to the structure built originally, For the backwards IRC, a molecule of ethylene and butadiene were reached. Note checkpoint files were always used for IRC analysis, as the log files often display the data incorrectly (point two on the IRC graph!).
| Forward Coordinate DOI:10042/to-8122 | Reverse Coordinate DOI:10042/to-8123 |
 |
 |
 |
 |
Because the IRC shows the reaction coordinate from the reactants to the products, it is plausible that the IRC coordinates can combined to give a (semi-)quantitative reaction plot. This was attempted, and the output is show below.
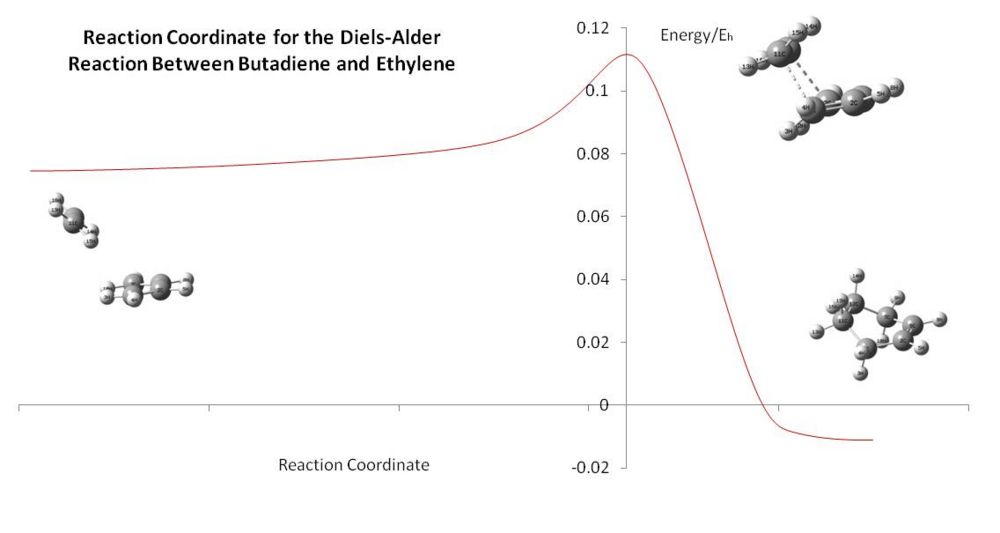
This is still only at the low AM1 level of calculation, so the data is probably poorly correlated to the literature, although it certainly gives a qualitative reaction plot. Obtaining high level calculation energies should allow the comparative data for the activation energies.
The reactants have a large, low-gradient period of approach, allowing them to prepare to react without too much of an energy penalty. Is could be suggested that this is therefore an early transition state as they resemble the transition state geometrically quite well (looking back at the bond lengths of the DFT TS, it can be seen that the forming double bond is still longer than the two double bond which are become single bonds, which also supports this theory). It is noticed that the minimum for the starting materials is when the reactants are still within interaction distance. Hence, there must be a slight stabilisation by being orientated in this conformation. This can be shown to be true by summing the energies of isolated fragments and finding a higher energy than the energy for the two fragments together. It is therefore hypothesised that the weaker interactions can direct the reagents together, the weak attraction of the two sets of H atoms in this case, and lead the ethylene in, with the symmetry aiding the route along the reaction coordinate. This is noted again for the exo reaction coordinate for the reaction of maleic anhydride and 1,3-cyclohexadiene.
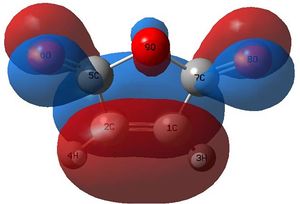
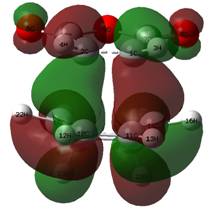
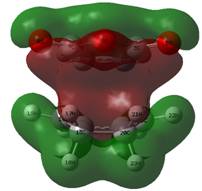
Examining the HOMO of the Transition State
 |
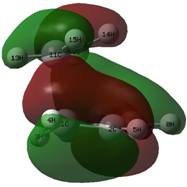 |
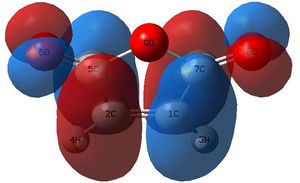
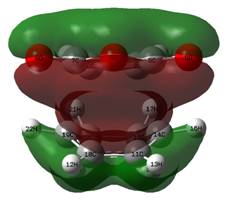
These MOs from the AM1 calculations show an excellent overlap of the HOMO of the butadiene with the LUMO of ethylene. However, when drawing an MO diagram from symmetry/first principles, this is not predicted to be the HOMO. The diagram below shows the predicted MO with the orbitals calculated at the DFT level. Note that more intricate mixing occurs, particularly with H fragments, and this is not shown on the diagram, which is based upon the frontier pi orbitals. This is why AM1 has different orbitals (lack of proper mixing). Here, the "antibonding" character of the HOMO is better displayed. Despite this, the HOMO is still stabilised (negative relative energy) and the reaction is therefore favourable. The HOMO from the AM1 method is now the HOMO - 1, which is the key stabilising interaction, as the antibonding version of this orbital is unoccupied. This can be compared to, for example, the two 2s orbitals interacting in a C-C bond; because the bonding and antibonding MOs formed through mixing are both occupied and low in energy, they do not contribute to the overall stabilisation of the bond. In this case, the split just happens to fall so the antibonding MO is just above the key stabilisation, thus it is the HOMO - 1 that contributes the bonding character of the forming sigma bonds.

These MOs are the full range of the MOs from MO 21 to MO 25. These orbitals are similar to those calculated at the (low) AM1 level, but some key differences are found. Firstly, the HOMO and the HOMO - 1 are reversed. Secondly, some of the orbital shapes/mixing effects are slightly different between models and thirdly, the HOMO - 2 in the AM1 model does not use pz orbitals (perpendicular to the double bond), unlike the DFT orbitals in the HOMO -2 above.
Higher Level Calculations for Activation Energy Determination
The starting materials were optimised at the DFT level and the energies summed (this is just an isomer of the constituent atoms in which no interaction between the two halves are modelled). These were compared to energies from DFT level calculations of the product and the transition state. The calculation level was DFT B3LYP/6-31G* and all calculations were ratified by a frequency analysis that returned no imaginary frequencies. The most stable butadiene conformer was used, the trans- conformer, at 298.15 K.
| energy(kcal/mol) | Sum of St mat (trans) | TS | lit.[6] TS | Product | lit.[6] Product |
| DFT Level Calculations | -234.580 | -234.544 | - | -234.648 | - 234.648 |
| Rel to Sum of isolated St mat (trans-butadiene and ethylene) | 0.00 | 22.40 | 27.5 | -43.11 | -40 |
The relative energy of the transition state to the sum of the isolated fragments (reactants) is equal to the transition barrier; 22.4 kcal/mol (lit.[6] 27.5 kcal/mol). The products are much more stable in energy (by 43. kcal/mol, lit.[6] 40 kcal/mol), so this is a favourable reaction. The literature values are in good agreement with the values found here, even at this level of theory and the literature also reports concludes that the reaction is synchronous, with the asynchronous mechanism ~2.3-7.7 kcal/mol higher in energy. However, it is noticed that other levels of theory, including MINDO/3 calculations[8] predict an asynchronous mechanism.
The literature [6] for B3LYP/6-31g* level calculations gives "- 234.64829", -78.58746 and -155.99214 a.u. for the optimised energy of cyclohexene, butadiene and ethylene, in exact agreement with the values found here.
Secondary Kinetic Isotope Effects
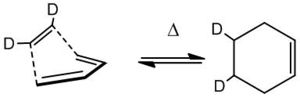
Substituting hydrogen atoms for deuterium atoms allows the observation of secondary kinetic isotope effects. Vibrational frequencies are inversely proportional to the reduced mass of a system, and so a C-H bond vibrates at a different energy compared to a C-D bond. When an isotope is substituted at a centre that changes geometry during the course of a reaction (and therefore the transition state), the activation energy can be affected as the zero point energies differ between the starting species (C-D ZPE is far below the ZPE for C-H) by a different amount than the transition states vary.
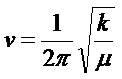
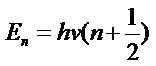
Reading the literature[9],[10],[11], indicated that a program called QUIVER was required to calculate secondary isotope effects, not available for these labs.
Calculations replacing 2 cis-hydrogen atoms (shown right) of ethylene with deuterium allowed the following observations to be made, although the SKIEs are not calculable easily using simple algebra.
For ethylene alone, the ZPE of the molecule at 298.15 K decreased from -78.536 to -78.542 a.u. (DFT B3LYP/6-31G*) when deuterating the molecule twice, a difference of 0.006 a.u. The transition state energy decreased from -234.403 a.u. (un-substituted) to -234.410 a.u. for the deuterated version at 298.15K, a difference of 0.007 a.u. This is ~0.3 kcal/mol change in the zero point energies from starting materials to transition state, which predicts the observation of SKIEs for this reaction (the energies of activation for the normal and substituted reactions should be different). The observed change in the imaginary vibration is from -524.79 (normal) to -524.15 (deuterated).
This is predicted, and for the two hydrogen atoms replaced, an inverse effect of 0.95 is calculated using this level of theory in the literature[6] using QUIVER (based on derivations by Bigeleisen and Mayer in transition state theory).
------------------- - Thermochemistry - ------------------- Temperature 298.150 Kelvin. Pressure 1.00000 Atm. ... ... Atom 12 has atomic number 6 and mass 12.00000 Atom 13 has atomic number 1 and mass 2.01410 Atom 14 has atomic number 1 and mass 1.00783 Atom 15 has atomic number 1 and mass 1.00783 Atom 16 has atomic number 1 and mass 2.01410
Whilst the above equations are being discussed, it is worth pointing out that the square root of the force constant is used to calculate the vibrational modes. For the negative force constant found at a transition state, the resulting frequency will be "imaginary" (rather than negative) as it is proportional to the square root of a negative number. At a transition point, there is one degree of freedom which has one imaginary frequency, which corresponds to the reaction coordinate to the reactants and product. Using a Taylor expansion about the equilibrium geometry, at equilibrium, the first derivative of the function is zero (stationary point on the curve), and the initial term, V(0), is also zero. Higher order terms tend to be negligible, leaving only the second derivative term. This term is equal to the potential energy where the derivative term is k,the force constant, in the above (right) equation, and the vibrational frequency is therefore proportional to the square root of this.
Summary
- The starting materials of ethylene and butadiene were optimised at the AM1 and DFT levels and the MOs examined.
- The transition state for the Diels-Alder reaction between ethylene and butadiene was found using then Berny Transition State Optimisation Method, which was ratified by the single negative frequency.
- IRC analysis was used to map the TS onto the reactants and products and the reaction coordinate plotted. The reaction coordinate against energy graph was as predicted and showed the products were significantly more stable than the reactants.
- The MOs of the TS were examined and their origins hypothesised on in an MO diagram. The AM1 HOMO was the HOMO - 1 at DFT level. It was suggested this was due to poor mixing simulations in the AM1 method.
- The high level theory (DFT/B3LYP-6-31G*) energy values were used to find the activation energy of the reaction, which was found to reproduce the literature values at the same level of theory, and agree very well with experimental values.
- Secondary Kinetic Isotope Effects (SKIEs) were investigated and it was predicted from simple isotope substitutions that the Diels-Alder reaction of butadiene and ethylene would show SKIEs. Literature values ratified this prediction, although the calculations were not feasible in the labs as the required software was not available.
Semi-Empirical + DFT Calculations to Probe the Mechanism of Maleic Anhydride with 1,3-Cyclohexadiene
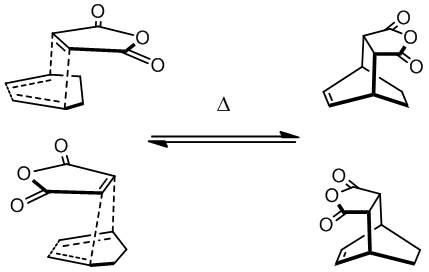
Outline of the Experiment
Many Diels-Alder reactions are known to give a kinetic endo- product, deemed due to secondary orbital effects and a thermodynamic exo- product which has less torsional strain and hence a lower energy structure.
In the reaction between maleic anhydride (MA) with 1,3-cyclohexadiene (CHD) using semi-empirical calculations at the AM1 level, neither of these statements were found to be consistent with the evidence. The endo- transition state was found to have a lower energy structure, but decisive secondary orbital effects were questionable. The endo- product was also found to be lower in energy than the exo- isomer, as the exo- isomer has a more eclipsed clash between MA fragment carbon atoms and the sp3 protons angled towards them (see later).
Experimental: Optimisation of the Starting Materials
Maleic anhydride was built in Gaussian and optimised using Gaussian at the AM1 and the DFT B3LYP/6-31G* level. 1,3-cyclohexadiene was built and optimised likewise. All optimisations were ratified by frequency analysis. These initial results are shown below. No other conformers were found, with a planar maleic anhydride and a C2 symmetric cyclohexadiene, with two energetically identical atropisomers.
| structure | Lowest Vib cm-1 | Energy / Eh | Lowest Vib cm-1 | Energy / Eh | Visualise |
| Cyclohexadiene DOI:10042/to-8124 | 191 | -233.419 | 100 | 0.028 | |
| Maleic Anhydride DOI:10042/to-8125 | 168 | -379.290 | 156 | -0.122 | |
| Sum | -612.708 | -0.094 |
Considering the Frontier Molecular Orbitals
The MOs of the reactants were examined (HOMO and LUMO) to check compatibility for reaction (via heat). There is a rough plane of symmetry, although the cyclohexadiene in not planar, so is only C2 symmetric, and not C2v.
The matched orbitals are outlined in the table and as for the previous reaction (butadiene with ethylene) the symmetrically equivalent orbitals are the HOMO of one fragment with the LUMO of the other.
Finding the Transition States

The optimise to a Berny TS method had worked well so far, so this was used again here. In this case, what was learned in the above example was applied. The exo- conformer TS was attempted first.
- Change sp2 centres that are becoming sp3 to nearer tetrahedral geometry, by changing the angles of the hydrogen atoms/substituents where necessary.
- Changing the new forming bond lengths to ~ 2.2 Å.
- Angling the two reactants with a plane of symmetry, as in the product.
- Angling the "attack" at 109.5o as might be expected in the TS.
The pre-optimisation geometry is shown right. The calculation was run using the following keywords:
# opt=(calcfc,ts,noeigen) freq am1 geom=connectivity
The optimisation was successful, with one imaginary frequency found, resembling the expected reaction coordinate. The optimised transition state was easily converted into that for the endo TS, by simply rotating the MA by 180o, and attempting to keep all other intermolecular distances equal. This was successful too, and the two transition states found are shown below.
| EXO DOI:10042/to-8127 |
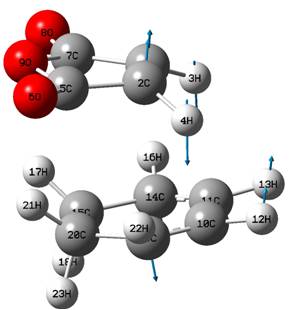 |
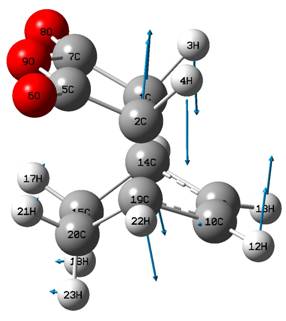 |
| ENDO DOI:10042/to-8126 |
 |
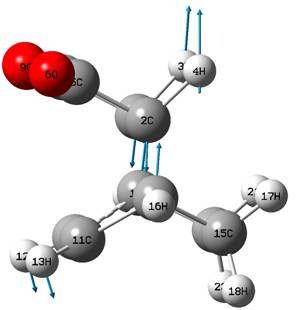 |
IRC Analysis of the Reaction Between MA and CHD
Again, to ensure transition state maps onto both the reactant and the product and IRC analysis was completed. The same criteria were used as before to converge, namely:
# irc=(forward,maxpoints=100,calcall) ram1 geom=connectivity
# irc=(reverse,maxpoints=100,calcall) ram1 geom=connectivity
The correct structures were found at either side of the transition states, giving credibility to the transition states found. The reactants, products and transition states were all re-optimised at a higher level - DFT B3LYP/6-31G*. The arbitrary nature of "forward" and "reverse" IRC labelling is inherent in the table!
| Isomer | Forward Coordinate | Reverse Coordinate |
| EXO | 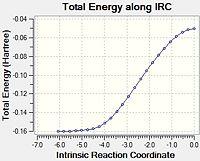 |
 |
| ENDO | 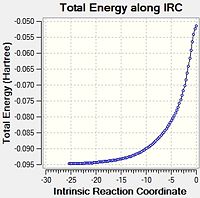 |
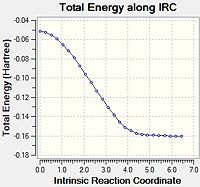 |
Again, the data was plotted to obtain an overall reaction energy diagram.

It is apparent that the energies are very close. The products seem almost identical, but the endo is slightly more stable. The exo TS is clearly higher in energy, and the direct result of the IRC back to the starting materials leaves MA and CHD in slightly different positions, leading to a slightly more stable starting energy for the exo reaction - there appears to be favourable interaction between the oxygen atoms on the MA and the hydrogen atoms at the sp3 centres on the CHD. Indeed, some literature states that pre-reactive vdW forces can affect the nature of the reaction[12]. At further distances, these energies will converge to the same value, the sum of the energies for the isolated structures. The following table sums up the energies and differences, as calculated at the DFT level.
The Energies of the Final DFT Level Optimised Structures: The Kinetic and Thermodynamic Products
The following are the energies and differences for the two isomers, starting materials, transition states and products (relative to the starting material) as calculated at the DFT B3LYP/6-31G* level.
| Eh | kcal/mol | |||||
| Energy St Mat | Energy TS | Energy Product | Rel to St Mat | TS Rel to St Mat | Prod Rel to St Mat | |
| ENDO DOI:10042/to-8180 | -612.71 | -612.68 | -612.76 | 0.00 | 15.74 | -31.19 |
| EXO DOI:10042/to-8181 | -612.71 | -612.68 | -612.76 | 0.00 | 18.30 | -29.68 |
The "TS Rel to St Mat" column also represents the activation energy (the energy barrier to the transition state from the reactants). The endo product has a smaller barrier (by 2.56 kcal/mol) and hence is the kinetic product. The endo product has a lower energy (by 1.51 kcal/mol), so is also the thermodynamic product in this case. Experimental data suggests this is the right ballpark (12.1 kcal/mol for a similar reaction)[13].
For cyclopentadiene, the thermodynamic product is reported to be the thermodynamic product, so there must be something in this structure that destabilises the exo or stabilises the endo product.
| ENDO | EXO | ||||||
|
| ||||||
|
|
The Jmols show how perhaps the exo product is less stable due to the proximity of the non-bonding carbon/hydrogen atoms as shown via the distance measurement. The spacefill model backs this up, with a much larger carbon to hydrogen van der Waals overlap for the exo product, a result of the MA fragment facing the sp3 carbons. The endo MA fragment faces the sp2 carbons, with most other parts of the two structures being identical.
It is reported[14] that the equivalent reaction, but with cyclopentadiene, has a TS 3.7 kcal/mol lower than the TS for cyclohexadiene. This is attributed to the distance between the carbons on the diene and the distortion energy required to reach the transition state.
Secondary Orbital Interactions?
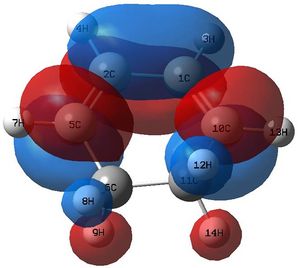
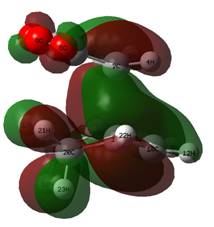
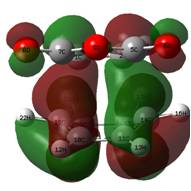
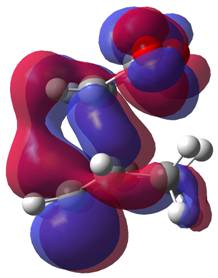
In this reaction the HOMO of the TS appears to be the LUMO of MA interacting with the HOMO of CHD. This is expected, as the electron poor dienophile, MA, has a low lying LUMO (due to the stability imparted in the molecule from the conjugation with the carbonyl p-orbitals) and CHD has a comparatively high HOMO. This close energy match means a large stabilisation, as predicted by the Klopman-Salem equation, which states that the stabilisation of interacting orbitals is inversely proportional to the energy gap between the interacting orbitals - a small gap means a large stabilisation.
The orbitals of these transition states were probed for the legendary secondary orbital interactions. No additional stabilisation was found in the HOMO and there are no p orbital contributions on the carbonyl carbon atoms of the MA below the plane of the molecule to interact with the forming double bond. The LUMO has a node between the two fragments, as for the butadiene example and so no interactions are possible here. The other orbitals were investigated to check for any favourable interactions. One bonding candidate was found, but this did not appear to be any better for the endo than it did the exo, as an analogous interaction existed, despite the lack of a double bond to do so (MOs 15 and 16), and on top of this, these orbitals are rather deep-seated to play significant roles in reactivity.
Examining the LUMO + 2 orbitals (below) shows what would be an emphatic secondary orbital effect for the endo over the exo (note the strong column of overlap between the p orbitals on the carbonyl oxygen atoms and the forming double bond below in the bottom left image, relative to the image above). However, as this is antibonding in character overall and destabilised relative to zero, it is difficult to envisage how this might act to stabilise the endo transition state.
Further Discussion of Secondary Orbitals Effects
The nature and pertinence of secondary orbital effects in relation to cycloaddition selectivity has been much discussed in the computational chemistry literature. From the original observation of Alder and Stein[15] for their endo rule ("maximum accumulation of double bonds"), many additional reasons have been proposed to explain relative transition state energies. These include Woodward and Hoffmann's so-called secondary orbital effects which have sparked much debate[16]. Various reviews have emerged[17] and computational experiments[18] have been performed to explain the selectivity in Diels-Alder reactions, and whilst it seems SOIs do really exist and play some part, they are not solely to blame for the prevalence of endo/exo products, and a recent review gives a whole host of possible alternatives.
The staple argument of van der Waals attractions[12] and sterical clashes are cited[17] as possible decisive contributors, as well as H-bonding, solvent effects and electrostatic forces. The authors of a review[17] claim that many attempts to explain an observed effect using SOIs are lazy scapegoat explanations without considering other, more provable alternatives.
Volumes of activation have also been explored, with a Diels-Alder reaction of maleic anhydride with 1,3-cyclohexadiene being claimed as one of the first reactions found with a negative volume of activation, relative to both the reagents and the products[19], although it seems that the differences in the volumes of activation between the exo and endo transition states are generally too small to invoke as an argument as to reactivity.
For the studied reaction, it is hard to pinpoint interactions that favour the endo TS. Qualitatively speaking, an argument for the favouring of the endo TS might be the so-called "sterics", but this is hard to rationalise by looking at the orbitals in the region. Combining the LUMO of MA with the HOMO of CHD simplistically gives the bond in the HOMO of the TS, but there appears to be less electron density on the carbonyl carbons so no secondary effect is observed here. The LUMO + 2 appears to be the only orbital that really discriminates between the endo and exo, and although organic chemists describe this as anti-bonding and unoccupied, it is supposed that fleeting instances of occupancy would stabilise the endo TS slightly above that of the exo, as these orbitals provide a degree of freedom in which to place electron density between the reacting fragments. However, it is more likely to be an accumulation of small additive effects that makes one isomer TS more stable than another.
Returning to the vdW argument presented above[12], it is plausible to suggest that, just as solvent can stabilise the reactants and decrease the rate of reaction, other reagents can interact favourably initially, decreasing tendency to want to complete the reaction. In this case, it was seen that the exo transition state IRC back to the reactants led to a stable, highly interacting configuration of reactants. The exo starting configuration was found to be 0.66 kcal/mol more stable than the endo starting configuration, which when combined with the more stable transition state for the endo isomer, provides a large decrease in the activation energy to the reaction, although it is recognised that such effects are not present for the isolated molecules.
Some of the largest contributors to reaction rates are known to be solvent effects. It is a common solution to run reactions which involve the destruction of two charges to make a neutral complex in a nonpolar solvent. The solvent cannot stabilise the reactants, pushing their initial energy up, towards the transition state, lowering the barrier to the reaction (ie, salt naturally tends to precipitate in organic solvents). Many authors have shown that computational theory and experiment do not always agree for cycloaddition reactions, and like to suggest solvent effects for this observation[20].
Investigating the Effect on the Transition State Energy on Changing the Solvent
Having concluded that the solvent in a wet lab experiment can cause large effects on the product outcome and transition state energies (not modelled in the computer simulations studied so far), a basic solvent model was added and the optimised TSs reanalysed for comparison to the "gas phase" type calculations completed so far. The IPCM model[21] has been reported to model such effects fairly well. Because the structures had already been optimised at the DFT level, these calculations required fairly short computational times. The following keywords were invoked to model solvent effects in water, benzene and DCM.
e.g. # opt=(calcfc,ts,noeigen) freq rb3lyp/6-31g(d) scrf=(iefpcm,solvent=benzene) geom=connectivity
Representative publications: (in water) ENDO DOI:10042/to-8182 , EXO DOI:10042/to-8183
| Water | DCM | Benzene | Gas | ||
| MAH | Energy / Eh | -379.299 | -379.298 | -379.294 | -379.290 |
| Rel to Gas (kcal/mol) | -6.24 | -5.27 | -2.78 | 0.00 | |
| CHD | Energy / Eh | -233.421 | -233.420 | -233.420 | -233.419 |
| Rel to Gas (kcal/mol) | -1.11 | -0.92 | -0.46 | 0.00 | |
| EXO Product | Energy / Eh | -612.766 | -612.765 | -612.760 | -612.756 |
| Rel to Gas (kcal/mol) | -6.48 | -5.47 | -2.90 | 0.00 | |
| ENDO Product | Energy / Eh | -612.769 | -612.768 | -612.763 | -612.758 |
| Rel to Gas (kcal/mol) | -7.06 | -7.47 | -4.68 | -1.51 | |
| EXO TS | Energy / Eh | -612.691 | -612.696 | -612.685 | -612.679 |
| Rel to Gas (kcal/mol) | -7.64 | -10.44 | -3.41 | 0.00 | |
| ENDO TS | Energy / Eh | -612.697 | -612.695 | -612.690 | -612.683 |
| Rel to Gas (kcal/mol) | -8.68 | -7.34 | -3.89 | 0.00 | |
| ST MAT - GAS (kcal/mol) | -7.35 | -6.19 | -3.24 | 0.00 | |
| EXO - ENDO (PRODUCT) (kcal/mol) | 2.09 | 2.00 | 1.79 | 1.51 | |
| Activation Energy (EXO) (kcal/mol) | 18.01 | 14.05 | 18.13 | 18.30 | |
| Activation Energy (ENDO) (kcal/mol) | 14.41 | 14.59 | 15.08 | 15.74 | |
| EXO - ENDO (TS) (kcal/mol) | 3.60 | -0.54 | 3.05 | 2.56 |
The starting material, transition state and product energies are plotted below, with the curves interpolated so each system can be readily identified. The key observations from the graph are that for all systems other than DCM, the (red) endo transition states are lower than the (blue) exo transition state. For DCM this is reversed, making the exo isomer the kinetic product in DCM, although it is very close (from the above table, the exo TS is 0.54 kcal/mol lower in energy than the endo). For all systems, the endo isomer is the thermodynamic product - the solvent cannot readily stabilise the sterical instability in the exo product. As expected, each solvent stabilises all structures relative to the "gas phase". Aqueous solutions are well reported[22] to increase the rate of Diels-Alder reactions, and this is observed here, although large scale solubility effects are not accounted for, and only hydrogen bonds can be said to stabilise the system; the "enforced hydrophobic interactions" are not modelled in this bi molecular system. Water also gives the biggest distinction between the endo and the exo transition states, making it the solvent of choice to obtain the endo product. DCM should be used under kinetic control to maximise yield of the exo isomer. No literature values could be found for comparison.

Conclusion
- Maleic anhydride (MA) and 1,3-cyclohexadiene (CHD) were optimised with AM1 semi-empirical calculations and DFT/B3LYP-6-31G* quantum mechanical calculations and the frontier molecular orbitals considered. The HOMO of CHD is allowed to mix with the LUMO of MA (as is the LUMO of CHD and the HOMO of MA, but these are energetically further apart).
- The transition states for the endo and exo isomers were found using the Optimise to a Berny Transition State Method in the AM1 method after augmenting the geometry of the starting materials and aligning the reactants carefully.
- The endo isomer was found to be the kinetic and thermodynamic product of the reaction after an IRC analysis had successfully mapped the reactants, TSs and products.
- The MOs of the transition states were investigated after re-optimising the transition states at the DFT level. Secondary orbital interactions found were in the LUMO + 2 to suggest why the endo isomer was a lower energy, but a simpler sterical argument was invoked.
- Secondary Orbital Interactions were discussed with reference to the literature and concluded to be a possible influence, but often not the dominating one. Here, a "sterical" argument may be applicable, but as solvent and bulk effects are not modelled, accumulative secondary effects seem plausible as a reason that the endo TS is more stable.
- Van der Waals attractive forces were also proposed in stabilising the exo starting configuration relative to the endo starting configuration, also reported in the literature for the reaction of maleic anhydride with cyclopentadiene, which would raise the effective barrier.
- Solvent effects were considered and DCM found to give the exo isomer as the kinetic product.
- Further investigation could be dedicated to photochemical allowed reactions[23], although this would require excited state calculations to be performed.
References
- ↑ O. Wiest, K. A. Black, K. N. Houk, J. Am. Chem. Soc., 1994, 116 (22), 10337 DOI:10.1021/ja00101a078
- ↑ 2.0 2.1 M. J. Goldstein, M. S. Benzon, J. Am. Chem. Soc., 1972, 94, 7149 DOI:10.1021/ja00775a046
- ↑ A. Bondi, J. Phys. Chem., 1964, 68, 451 DOI:10.1021/j100785a001
- ↑ S. S. Batsanov, Journal of Molecular Structure: THEOCHEM, 1999, 468 (1-2), 151 DOI:10.1016/S0166-1280(99)00077-9
- ↑ D. R. Lide, Tetrahedron, 1962, 17 (3-4), 125 DOI:10.1016/S0040-4020(01)99012-X
- ↑ 6.0 6.1 6.2 6.3 6.4 6.5 6.6 E. Goldstein, B. Beno, K. N. Houk, J. Am. Chem. Soc., 1996, 118, 6043 DOI:10.1021/ja9601494
- ↑ C. Spino, M. Pesant, Y. Dory, Angewandte Chemie, 1998, 110, 3454
- ↑ M. J. S. Dewar, S. Olivella, H. S. Rzepa, J. Am. Chem. Soc., 1978, 100, 5659 DOI:10.1021/ja00486a013
- ↑ M. Saunders, K. E. Laidig, M. Wolfsberg, J. Am. Chem. Soc., 1989, 111, 8994 DOI:10.1021/ja00207a001
- ↑ K. N. Houk, S. M. Gustafson, K. A. Black, J. Am. Chem. Soc., 1992, 114, 8572 DOI:10.1021/ja00048a032
- ↑ J. W. Storer, L. Raimondi, K. N. Houk, J. Am. Chem. Soc., 1994, 116, 9683 DOI:10.1021/ja00100a037
- ↑ 12.0 12.1 12.2 D. Suárez, J. A. Sordo, Chem. Commun., 1998, 3, 385 DOI:10.1039/A707086A
- ↑ K. Nagai, H. Yonezawa, Journal of Polymer Science: Polymer Letters Edition, 1983, 21, 115 DOI:10.1002/pol.1983.130210208
- ↑ M. Ahmad, J. Hamer, J. Org. Chem., 1966, 31, 2833 DOI:10.1021/jo01347a022
- ↑ K. Alder, G. Stein, Justus Liebigs Annalen der Chemie, 1934, 514, 1 DOI:10.1002/jlac.19345140102
- ↑ R. Hoffmann, R. B. Woodward, J. Am. Chem. Soc., 1965, 87, 4389 DOI:10.1021/ja00947a033
- ↑ 17.0 17.1 17.2 J. I. García, J. A. Mayoral, L. Salvatella, Acc. Chem. Res., 2000, 33, 664 DOI:10.1021/ar0000152
- ↑ C. S. Wannere, A. Paul, R. Herges, K. N. Houk, H. F. Schaefer, P. Von Ragué Schleyer, Journal of Computational Chemistry, 2007, 28, 344 DOI:10.1002/jcc.20532
- ↑ R. A. Grieger, C. A. Eckert, J. Am. Chem. Soc., 1970, 92, 2919 DOI:10.1021/ja00712a054
- ↑ T. Karcher, W. Sicking, J. Sauer, R. Sustmann, Tetrahedron Letters, 1992, 33 (52), 8027 DOI:10.1016/S0040-4039(00)74708-3
- ↑ J. I. García, J. A. Mayoral, L. Salvatella, Tetrahedron, 1997, 53 (17), 6057 DOI:10.1016/S0040-4020(97)00255-X
- ↑ S. Otto, J. B. F. N. Engberts, Pure Appl. Chem., 2000, 72, 1365, DOI:10.1351/pac200072071207
- ↑ R. B. Woodward and R. Hoffmann, Angewandte Chemie International Edition in English, 1969, 8, 781 DOI:10.1002/anie.196907811
Final Edit: Kga08 16:57, 25 March 2011 (UTC)
EXPERIMENTALISTS THINK SILICON IS REALLY FUN TO USE
ITS PLACE IN NOVEL COMPOUNDS IS CERTAIN TO AMUSE
THEY SIT ALL DAY IN LABORATORIES MAKING ALL THIS SLUDGE
"LOADED WITH THE SILICON THEY SAY", TO ME IT LOOKS LIKE FUDGE.
FOR HAPPY THOUGH THEY BE WITH CRUD, I'D LIKE TO KNOW A LITTLE
ABOUT THE PI BONDS ON THE EDGE AND SIGMAS IN THE MIDDLE.
SO LETS DERIVE A WAVEFUNCTION.....6-31G*
USE AN OPTIMAL GEOMETRY AND SEE WHERE ELECTRONS ARE.
BUT WHAT OF CORRELATION? ASKS THE WIRY LITTLE SKEPTIC.
WE'LL THROW IN PERTURBATION AS AN ELECTRON ANTISEPTIC.
AND WHEN THE PROGRAM GIVES US ANSWERS IN THEM WE CAN TRUST
SINCE NOBODY CAN MAKE THE STUFF, WE HAVE NO CHOICE, WE MUST.
SO THEORY GUYS HAVE GOT IT MADE, IN ROOMS FREE OF POLLUTION.
INSTEAD OF PROBLEMS WITH THE REFLUX, THEY HAVE ONLY SOLUTIONS.
AND WHEN THE FEDS ANNOUNCE THE LIST OF CARCINOGENIC TERRORS,
THE THEORISTS SIT SAFELY AT THEIR TERMINALS FIXING ERRORS.
IN OTHER WORDS, EXPERIMENTALISTS WILL LIKELY DIE OF CANCER
FROM WORKING HARD YET FRUITLESSLY...TILL THEORY GIVES THE ANSWER.
-- THOMAS A. HOLME, 1983