Rep:Mod:kga08module1wiki

Introduction: An Overview of Computational Chemistry; A Series of Molecular Modelling Exercises For Real Life Application by Keith Andrews

Since Allinger's gift of molecular mechanics to the chemical community with the invention of Molecular Mechanics 1 (MM1), and later MM2, the field has grown to the stage that most published works that have potential for a computational compliment to the wet lab experimental results, do include such data. With the increase in computing power, quantum mechanical calculations are now feasible on desktop computers, although some calculations may take hours and days to complete to worthwhile standards.

The molecular mechanics equation takes the form of non-interacting but additive energy terms, which are output in terms relative to expected data based on empirical observations such as bond lengths etc. This means the program truly is only as good as the knowledge behind it, and therefore is restricted to known chemistry, interpolating rather than extrapolating intelligently. The results obtained from MM2, for example, whilst partially quantitative relative to similar calculations by the same force field, are not applicable to any observables or calculations by different equations/forcefields. Further, the calculations are only possible if the parameters between defined atoms are available, although many of the key combinations (start of the periodic table) are included in the software. Finally, due to the quadratic format, the bonds are unable to be broken - the energy keeps on increasing to infinity with further displacement from ideality. An excellent overview is given here.

Whilst good at determining geometries (the van der Waals terms are particularly acute), electrons are ignored explicitly, and molecular orbital effects are not accounted for. Semi-empirical calculations (eg. PM6) make a good compliment to MM2 for calculating orbitals, which can be helpful in explaining reactivity.

This Wiki page describes several approaches to computational techniques and attempts to explore the capabilities and limitations of the methods used with reference to the literature for guidance in accuracy/applicability.

Also:

• A link was added to the writeup page to assist future users with Jmol script.
• A second link was added to the Mod:organic page with a list of defined solvents for the NMR section (scroll to bottom).
• A short macro-assisted program written in MS Excel was used to produce the wiki-formatted references. When this program has been made user-friendly, a version may be uploaded onto the wiki for future users to easily obtain the wiki-formatted reference text; I am unaware of a current alternative.
• Tables were produced in excel, converted using an exceltowiki converter and then edited slightly within wiki to the style desired.
• Tables appearing in the wiki often show (relative values) - the numerical difference between two columns. Again, a template designed in Excel was used to efficiently make these tables using the concatenate function. Further spreadsheet formulas were used to extract the relevant NMR figures data from the output text files obtained from Gaussian. These too may be uploaded at some point to assist data manipulation, and eliminate copying errors.

(note this wiki was made on a fairly widescreen computer and may incur formatting discrepancies if viewed on narrower screens) (all energies are quoted in the conventional kcal/mol for ease of comparison to other computational results)

Hydrogenation of the Cyclopentadiene Dimer

The Endo Dimer: Structure 1

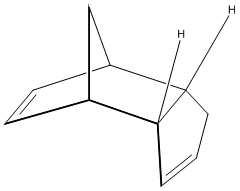
Outline

The Diels-Alder dimerisation of cyclopentadiene has been long known to give primarily the endo product. Here, molecular mechanics calculations (MM2) are used to shown that this must be a kinetic effect, as opposed to a thermodynamic effect, and the contributing energies will be contrasted to highlight the origin of the relative instability of the endo product. Finally, the differences in the reactivity of the two alkenes (within the endo molecule) toward hydrogenation is considered and the products compared in energy to assess stability.

The Exo Dimer: Structure 2

The Diels-Alder Reaction

The Nobel Prize winning Diels-Alder reaction was formulated in 1928 and remains an extensively used, incredibly powerful, carbon-carbon connecting reaction, more recently applied to heteroatom-containing functionalities. As early as 1942, an extensive review of the diene synthesis (or Diels-Alder reaction) was published, with details of endo and exo selectivity already being discussed. For the [_π4_s + _π2_s] cycloaddition of cyclopentadiene, by eye, a keen chemist would intuitively single out the endo isomer as being the more strained, less favoured conformation, and this is indeed what thermodynamic calculations predict. However, the endo product is often isolated as the product of the Diels-Alder reaction for reagents such as maleic anhydride and the dimerisation of cyclopentadiene, as described in this section. For substrates that can donate non-bonding electron density into the forming double bond at in the new six-membered ring, the endo product can indulge in a faster formation rate due to a lower energy transition state. That this is indeed a kinetic effect is shown by eliminating the thermodynamic option - if the exo product is more stable, then the endo product must be formed as the kinetic product to form at all (and be isolated). For now, molecular mechanics can prove only this much, and the "secondary orbital effects" that allow this kinetic product to form are left untreated.

Experimental: Comparing Endo and Exo Isomers

The endo and exo structures were both drawn with reasonable accuracy in ChemBio3D and the MM2 molecular mechanics algorithms run to minimise the energy of each molecule. The data is presented in the tables and shows that the exo dimer is lower in energy that the endo dimer by 2.12 kcal/mol. With the aforementioned knowledge that the endo isomer predominates, it is therefore shown that as the endo isomer is less stable; its proliferation in the Diels-Alder reaction must be via a kinetic pathway. This requires a lower energy of activation, and this is indeed quoted experimentally as being 33.0 kcal/mol for the endo isomer and 37.4 kcal/mol for the exo isomer, which is in full agreement with a kinetic argument. More specifically, the torsion and van der Waals terms distinguish the two isomers. The torsion is apparent in the bending back of the endo structure on itself, eclipsing sets of carbons (see Visualise button in the image, right) (dihedral = 45^o) and the van der Waals term is likely high due to the close carbon carbon contacts of 2.86 Å; 3.2 Å is closer to the maximum attractive interaction (navigate to alkanes along the top and scroll down).

Hydrogenation Products

Relative Energies of the Cyclopentadiene Dimers

Energy in (kcal/mol)
	Exo [Structure 2] (relative to Exo)	Endo [Structure 1] (relative to Exo)
Stretch	1.2774 (0)	1.2519 (-0.0255)
Bend	20.5637 (0)	20.847 (0.2833)
Stretch-Bend	-0.8366 (0)	-0.8383 (-0.0017)
Torsion	7.6618 (0)	9.5139 (1.8521)
Non-1,4 VDW	-1.4021 (0)	-1.5559 (-0.1538)
1,4 VDW	-1.4021 (0)	4.3341 (5.7362)
Dipole/Dipole	0.3777 (0)	0.449 (0.0713)
Total Energy	31.8793 (0)	34.0016 (2.1223)
	Total Difference	2.1223

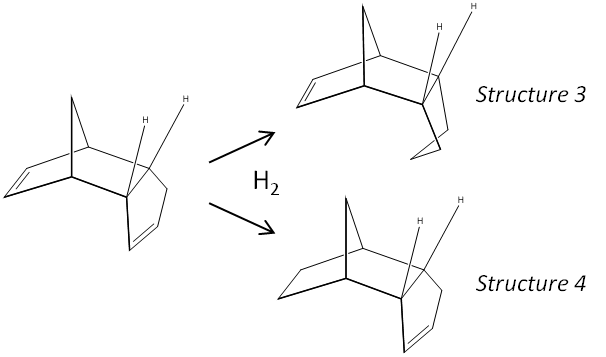
Experimental: Hydrogenation of the Endo Isomer

The second table shows the relative energies of the mono-hydrogenatated isomers of the endo dimer. There is a large energetic disfavouring of structure 3 (hydrogenation of the 5-membered ring) by 4.77 kcal/mol, which is mostly contributed to by the relative bending energies (the bending energy is 4.45 kcal/mol higher in energy for structure 3 compared to structure 4).

Relative Energies of the mono-Hydrogenation Products

Energy in (kcal/mol)
	Structure 3 (relative to 3)	Structure 4 (relative to 3)
Stretch	1.2347 (0)	1.1021 (-0.1326)
Bend	18.9656 (0)	14.5204 (-4.4452)
Stretch-Bend	-0.7605 (0)	-0.5477 (0.2128)
Torsion	12.1493 (0)	12.505 (0.3557)
Non-1,4 VDW	-1.5544 (0)	-1.0624 (0.492)
1,4 VDW	5.7329 (0)	4.5026 (-1.2303)
Dipole/Dipole	0.1632 (0)	0.1407 (-0.0225)
Total Energy	35.9307 (0)	31.1607 (-4.77)
	Total Difference	-4.7700

The internal bond angles of the alkene moiety of each hydrogenation product can be measured after geometry optimisation in ChemBio3D. The C-C-C alkene internal angle (cyclohexene) of structure 3 is found to be 107.6 + 107.6^o and the angles for the cyclopentene(structure 4) are 112.4 + 113.1^o . Ideally, the bond angles should be 120^o for sp² geometry, and it seems that both structures are strained due to the ring conformation, with the cyclopentene closer to the ideal geometry, which supports the overall thermodynamic stability implied from the overall energies. (The total energies assert that the cyclopentene (4) is the lower energy isomer). Looking into the energy contributions, it is seen that the bend term is the greatest contributor to the overall difference (4.45 kcal/mol), and this term takes into account the bond angle deformations as described above in terms of hybridisation. Whilst the kinetic product cannot be directly inferred from this analysis, it is concluded that the thermodynamically favoured product is the cyclopentene isomer. Perhaps, the kinetics might be related to the strain in the original endo molecule - the hydrogenation may be faster (have a lower barrier) on the more strained ring, which would also yield the thermodynamically favoured structure. (This argument assumes that the transition states of each reaction are of similar energy, meaning the reaction with the lower barrier is the one with the least stable reactants (which therefore start closer to the top of the barrier to reaction). Alternatively, the steric crowding of the cyclohexene might mean a faster rate of hydrogenation of the cyclopentene.

---

Investigating the Stereo+Regioselectivity of a Nucleophilic Addition by Considering the Lowest Energy Conformation of the Starting Material

Use of a Chiral Auxiliary in Asymmetric Synthesis

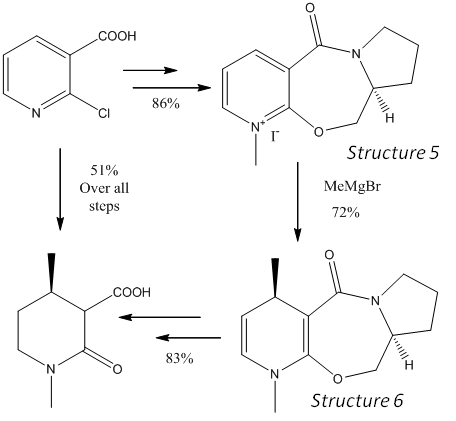
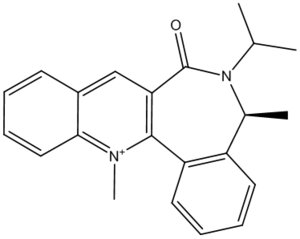
The use of chiral auxiliaries is a powerful technique for introducing chiral centres. The reaction in this section benefits from a chelation effect of a Grignard reagent with a carbonyl group, which is conformationally locked to favour the formation of one stereoisomer over another. The reaction of MeMgI with a pyridinium system proceeds with the stereochemistry shown in a reaction inspired by work in introducing chiral centres in dihydropyridines, and molecular modelling and basic quantum mechanical calculations will be used to suggest where this selectivity may originate.

Use of Chiral Auxiliaries

The reaction shown is reported experimentally to favour the para addition over the ortho addition by 19:1, with a complete selectivity of the shown stereoisomer. The product is in fact one diastereoisomer, due to the second chiral centre on the chiral auxiliary. The entire right hand side of the molecule is added just to effect the controlled methylation and is subsequently removed to give the final product in 83% over two steps.

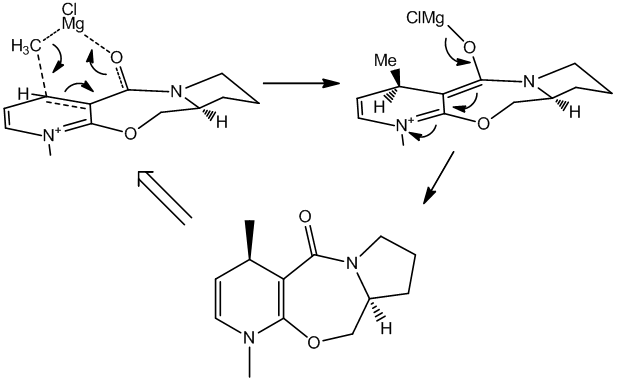
The key reaction is the Grignard addition reaction and the conformation of the reacting molecule must be considered to gain insight into the reasons for such selectivity. An initial clue is in the the regioselectivity; there is barely any ortho product, despite its apparent relative ease of access, sterically. A second clue is in the lack of selectivity seen in the more reactive MeLi species, which gives equal 1:1 para to ortho and only 3(desired):1 stereoselectivity. The decreased reaction rate when using the Grignard reagent (c.f. MeLi) and the more gentle chelation of the magnesium to the carbonyl adjacent provides a clear mechanistic explanation to the predominantly observed para product. But to give the desired top-face-delivery, the carbonyl must direct the alkyl-magnesium nucleophile. Molecular mechanics is used to show this.

Conformation of the Structure

Proposed Mechanism

Two contenders arise for the lowest energy conformation of structure 5, with the only difference being the "tip" of the cyclopentyl group on the right of the molecule. Each molecule was optimised using MM2, MMFF94 (a variant mechanics method) and PM6, a semi-empirical method and the results are outlined in the table below.

Energy Contributions to the Most Stable Prolinol Conformer and dihedral angle of the CO-Py System (tip down values on left)

Energy in (kcal/mol)
	Envelope Tip Down			Envelope Tip Up
	MM2 (relative to tip down)	MMFF94	PM6	MM2 (relative to tip down)	MMFF94	PM6
Stretch	1.8151 (0)	-	-	1.8381 (0.023)	-	-
Bend	14.2674 (0)	-	-	14.3384 (0.071)	-	-
Stretch-Bend	0.1153 (0)	-	-	0.146 (0.0307)	-	-
Torsion	5.099 (0)	-	-	6.0265 (0.9275)	-	-
Non-1,4 VDW	-0.5727 (0)	-	-	-0.4606 (0.1121)	-	-
1,4 VDW	16.6372 (0)	-	-	16.806 (0.1688)	-	-
Charge/Dipole	1.6837 (0)	-	-	1.753 (0.0693)	-	-
Dipole/Dipole	-3.9934 (0)	-	-	-3.9522 (0.0412)	-	-
Total Energy	35.0516 (0)	57.4493 (0)	-	36.5498 (1.4982)	59.0094 (1.5601)	-
Heat of Formation	-	-	93.8947 (0)	-	-	93.6866 (-0.2081)
dihedral angle/o	10	16	25	11	24	28

Firstly, it must be noted that no quantitative comparison between the different calculation methods can be made, only relative differences within each model. The resulting dihedral angles can of course be contrasted. The dihedral angle of the C-C-C=O system is 10^o forwards for MM2, with the angle increasing with MMFF94 and the PM6 calculation methods. That is to say that the carbonyl is slightly orientated forward, the same face that the nucleophile is delivered to and each method agrees. An error in the way MM2 calculates the energy for molecules containing an N⁺ group means this modelling must not be believed all too easily (the output states: "Warning; some parameters are guessed (Quality = 1)" - Quality = 4 is ideal. This refers to the lack of parameters for the N⁺ atom.). The complimentary calculation methods, however, supply sufficiently agreeable dihedral angles.

The method to accessing the lowest energy state involved carefully examining all local molecular conformers - the carbonyl orientation arises as a result of the combined efforts of the rest of the molecule. Firstly, the cyclopentane ring system on the right of the molecule can have it's "tip" up or down, with down being favoured (down relative to the face of attack to obtain the product stereochemistry). With the envelope tip up, the energy increases by ~1 kcal/mol for MM2 (angle = 11^o), ~1.5 kcal/mol for MMFF94 (angle = 24^o) and the Heat of Formation for the PM6 method decreases slightly, indicating a less stable product (angle = 28^o). Particularly of note here is that the qualitative result does not change; the carbonyl is for each method still up. These conformers are only slightly different in energy and the contributions are spread across most categories in the table. Torsion is slightly higher but again there appears to be no single contributing interaction - it is hard to pick out a truly unfavoured eclipsed conformation in one molecule relative to the other.

Secondly, and perhaps more significantly, is the position of the methylene carbon α to the ether oxygen. This can be moved from above the 7-ring to below it, however, there appears to be no conformation possible without altering the predefined stereochemistry at the other chiral centre that allows this - the ring is rigid and locked. If this stereochemistry is changed, the carbonyl moves below the plane of the pyridinium ring, and the stability of the system is comparable to the first molecule discussed. This would indicate that the chiral auxiliary can be used, with the opposite initial enantiomer, to effect methylation on the opposite face. This would be plausible if the mechanism is as expected, as the C-C-C-O dihedral angle is now -11^o; behind the ring plane.

Because the software used doesn't contain all parameters, less common elements cannot be modelled. In this case, the parameters required to solve the magnesium atom are not part of the software so the chelation effect cannot be observed in any way. The parameters are quite likely to exist somewhere, then they could be put into the MM2 parameter list to solve the energy and geometry.

Mechanistic Analysis

Because the mechanism outlined (right, above) does not directly involve quenching the positive charge on the N⁺ group (which would be a cause of directing ortho and para), it goes some way to explaining the very low ortho product count seen. More pertinent is the top-face delivery which is completed with near perfect selectivity. The chelation seems of utmost important, particularly given the low selectivity of the alkyl-lithium nucleophile as discussed above. This is an exemplary case of both substrate and reagent control; the favoured conformer (of the substrate) provides a foothold on the top face and the chelation mechanism (of the reagent) is complimentary.

Basic Structure, a NAD⁺ Derivative

---

A Second Example of a Nucleophilic Addition to a Conformationally Controlled Substrate

Nucleophilic Attack on the Quinoline Carbon para to N; Structures 7 and 8 Respectively

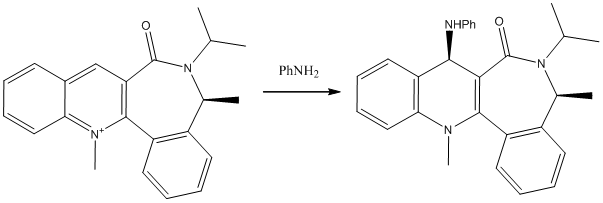
A similar example with a seemingly analogous nucleophilic addition via attack at the para position on a pyridinium ion leads to opposite stereochemistry being observed in the product. Again, the positive nitrogen element of the structure means the MM2 data cannot stand alone as fact. MMFF94 and PM6 calculations were run to compliment the data collected in this case. Again, a key factor distinguishing comparably stable conformers is the carbonyl dihedral angle, which again can be above or below the plane of the N-methyl quinoline, when drawn with the quinoline on the left, as shown.

Identifying the Most Stable Conformer; An Exercise in Efficiency

CO down Conformer with dihedral angle = -20^o

CO up Conformer with dihedral angle = +20^o

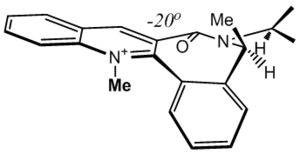
The process to finding the correct structure here took much endeavour in that, because of the energy minimising method MM2 uses, it is quite easy to get stuck in one of the two major conformations (CO up, or CO down). Of course, if the major conformations are not pre-known, as is expected in a real problem solving situation, a methodological and efficient technique in accounting for all possible permutations is required. There are several tricks that can be used that greatly reduce stress.

• Firstly, the way in which the molecule is constructed can determine the outcome. Particularly in ring type systems where, for example, chair and boat and other such conformers are possible, altering the order in which side groups are added can mean the difference between one form or another.

• Secondly, it can help to draw key parts of the molecule, and work on the possible conformers that (for example) the body can take before branching out with side chains and functionalisation.

• Finally, fine tuning allows more accurate numbers, which may be important when similar conformers produce similar energies. This can be done by increasing the accuracy the MM2 calculations are solved to by decreasing the Minimum RMS Gradient from 0.100 to 0.001. The Dihedral Driver can also be used to maximise the stability of side groups when the body has its major shape in place, by selecting two atoms at a rotatable junction, running the driver, and clicking on the minima desired.

This molecule is a perfect example of the care needed to extract the lowest energy conformer, which hinges on the way the methyl-bearing carbon alpha to the amide is positioned. The two major conformers are shown, one that has the carbonyl up and one that has the carbonyl down. These are again, merely consequences of the geometry of the rest of the molecule. The aforementioned methyl can be seen to dramatically change its orientation in the molecule, and the iso-propyl orientates itself differently in each molecule; the proton is either angled towards the carbonyl, or away from it, a consequence of the methyl's dominating jurisdiction. The fine tuning mentioned was applied here on both methyls and the iso-propyl using the dihedral driver; one graph is shown. The importance of carefully applying this method can be seen in the graph - although the major troughs in this case have similar energies and the outcome is not deeply affected, the cumulative effect seen if many of these false minima occurred in one structure would be detrimental to the final outcome, so ensuring each local environment is minimised is very important. This graph also has two small false minima that would raise the total energy significantly if the molecule was to be trapped in one.

Experimental: Methods of Optimisation of the Structures

Again, due to the N⁺, MMFF94 and PM6 were used to back up the possibly-deviating results obtained using MM2. (the dihedral driver graph is known to sometimes appear above the table - no data is under it!)

Relative Energies of the Conformations of an NADH⁺ Derivative

Energy in (kcal/mol)
	CO Down			CO Up
	MM2 (relative to CO Down)	MMFF94	PM6	MM2 (relative to CO Up)	MMFF94	PM6
Stretch	3.9646 (0)	-	-	4.0527 (0.0881)	-	-
Bend	11.5982 (0)	-	-	13.2721 (1.6739)	-	-
Stretch-Bend	0.4018 (0)	-	-	0.4354 (0.0336)	-	-
Torsion	9.5918 (0)	-	-	10.404 (0.8122)	-	-
Non-1,4 VDW	3.4527 (0)	-	-	4.5404 (1.0877)	-	-
1,4 VDW	29.3937 (0)	-	-	29.1934 (-0.2003)	-	-
Charge/Dipole	9.0582 (0)	-	-	9.2936 (0.2354)	-	-
Dipole/Dipole	-4.8874 (0)	-	-	-4.8715 (0.0159)	-	-
Total Energy	62.5736 (0)	98.3645 (0)	-	66.3201 (3.7465)	101.754 (-3.3895)	-
Heat of Formation	-	-	155.46232 (0)	-	-	157.44281 (-1.9805)
dihedral angle/o	20	34	45	-20	-36	-41

What do the Calculations Tell Us?

Relating these calculations back to the previously analysed molecule (structure 5), a similar trend arises. MMFF94 and PM6 both exaggerate the results given by the MM2 method, particularly the C(quinoline)-C(quinoline)-C(O)-O dihedral angle in this case (as shown in the Visualise applets). Each conformer produces roughly the same angle (for that modelling system), but negative, for the reverse conformer (CO forward(+) to back(-)) and each (modelling system) reaches the same conclusion. MM2, which is viewed with caution due to the positive ion, suggests that the CO back is favoured by 3.75 kcal/mol and MMFF94 supports this result. PM6 however is a close-run-thing, only just supporting the CO back result. It is concluded, however, that this is the expected conformer, and that somehow this affects the stereochemistry seen in the reaction, introduced below. Finally, a note on the contributing terms - the bend and VDW terms are the most different terms, but there does not appear to be any singly contributing part to these terms when examining the geometries.

A Stereoselective Reaction and Mechanistic Analysis

Recent attempts to uncover enzymatic mechanisms, specifically NADH coenzymes, and the impressive stereospecificity they impart in reduction processes, has led to the investigation of chiral amine transfer agents. Here the focus is on how the transfer agent is activated (see reaction outline above). Aniline is attached to the para position on the quinoline type structure with utmost specificity, and the product is used to transfer the aniline group to the desired substrate. We are part way to elucidating the chemistry behind the success, having established that the major conformer has the CO on the back face (as drawn), as opposed to the forward face, which is a slightly higher energy conformer.

Space Fill Model Showing CO Hindrance

Mechanism; attack onto the top face

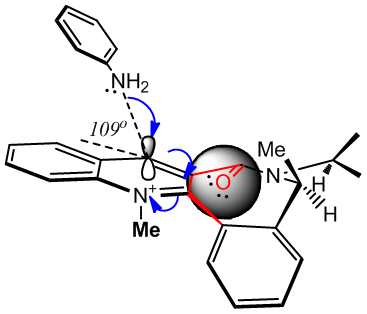
As shown in the above Jmol applet, the carbonyl oxygen spacefill style shows how the orientation of the carbonyl affects the steric environment around the para carbon to be attacked. Whilst the over hanging methyl group might slow the rate of attack down on the forward face (from the fairly large aniline), the alternative face might be expected to stave off attack by the amine lone pair by electrostatic repulsion [(C)=O:: lone pairs] and prevent all but the most eager assault on this face (>95%de). Having the CO back would seem to be a much bigger deterrent due to its proximity, whilst the overhanging methyl on the front face may slightly sacrifice rate for selectivity (it assists in forcing the necessary conformation.)

Reactivity of a Taxol Intermediate: Atropisomerism

The Structure of a Taxol Intermediate - CO up; structure 9

The Structure of a Taxol Intermediate - CO down; structure 10

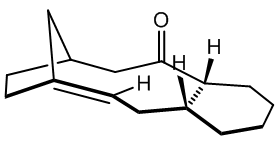
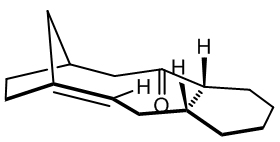
Atropisomerism arises when a single molecular structure has more than one deep minimum on its energy curve, with the barrier to the other minim(a/um) high enough to prevent interconversion at a given temperature. This is often a rotational barrier, prevented for example by steric bulk on adjacent side groups, or by a rigid framework that is slow to explore possible structures. The taxol intermediate shown has two key atropisomers, one with the CO up and one with the CO down, which slowly inter-convert to the most stable atropisomer at room temperature. Molecular modelling is fruitful in elucidating mechanisms behind stereochemical selectivity in situations in which the reactive moiety has multiple possible environments, as is here. The final (most stable) atropisomer of the taxol intermediate undergoes much slower functionalisation of the alkene than might be expected, given the strained nature of the (bridgehead) alkene, and molecular mechanics will be used to attempt to explain this phenomenon.

Conformational Analysis Using Molecular Mechanics

Carbonyl Up, Cyclohexyl Chair

Shown are the conformations for the carbonyl up (structure 9) and carbonyl down (structure 10) atropisomers, for which there exists no official nomenclature, due to the differing case by case nature of occurrence. For the carbonyl down atropisomer, two clear chair conformations are found, one with higher energy than the carbonyl up optimum geometry, and one with lower energy than carbonyl up. There is also a fairly stable twist boat of energy 48.1931 kcal/mol. The carbonyl up atropisomer appeared to have only one key conformer, the chair as shown. A second chair was only possible by inverting the stereochemistry of one of the up protons as drawn in the initial general structure, and the strained twist boat found did not compete in terms of stability.

Relative Energies of the Conformers of a Taxol Intermediate

Energy in (kcal/mol)
	Carbonyl Up			Carbonyl Down - Chair 1			Carbonyl Down - Chair 2
	MM2 (relative to CO up)	MMFF94	PM6	MM2 (relative to CO up)	MMFF94	PM6	MM2 (relative to CO up)	MMFF94	P6
Stretch	2.6714 (0)	-	-	2.568 (-0.1034)	-	-	3.0548 (0.3834)	-	-
Bend	15.8564 (0)	-	-	10.7789 (-5.0775)	-	-	14.9187 (-0.9377)	-	-
Stretch-Bend	0.3951 (0)	-	-	0.3226 (-0.0725)	-	-	0.36 (-0.0351)	-	-
Torsion	18.203 (0)	-	-	19.6035 (1.4005)	-	-	21.4467 (3.2437)	-	-
Non-1,4 VDW	-1.0572 (0)	-	-	-1.3575 (-0.3003)	-	-	-0.1849 (0.8723)	-	-
1,4 VDW	12.6624 (0)	-	-	12.5499 (-0.1125)	-	-	13.6166 (0.9542)	-	-
Dipole/Dipole	0.1483 (0)	-	-	-0.1834 (-0.3317)	-	-	-0.0375 (-0.1858)	-	-
Total Energy	48.8795 (0)	70.5392 (0)	-	44.282 (-4.5975)	60.558 (-9.9812)	-	53.1744 (4.2949)	74.7544 (4.2152)	-
Heat of Formation	-	-	-61.505 (0)	-	-	-65.071 (-3.566)	-	-	-56.414 (5.091)
Alkene Dihedral Angle 1/o	11	16	20	12	18	25	13	24	29
C(CO)C sp2 Angle/o	126	123	124	120	118	117	124	121	122
Alkene Ext. Bridge Angle 1/o	108	107	107	108	108	108	109	108	108
Alkene Dihedral Angle 2/o	-	-	-	11.7	-	-	15.4	-	-

Carbonyl Down, two Cyclohexyl Chairs

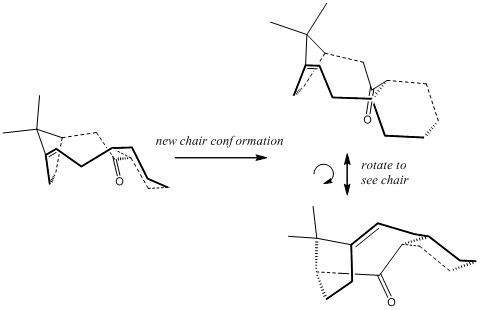
The twist boat form found for the cyclohexane ring (CO up) is higher in energy (54.0960 kcal/mol) and is not shown in the table. The MM2 method calculates this molecule much better than the previous attempts as there is no charged atom now. MM2 shows that the lowest energy conformer/atropisomer is the "first" chair form of the carbonyl down system. Various angles were included in the table, concentrating on the sp² carbonyl carbon and the strain on the alkene. These will prove useful in considering the functionalisation (hydrogenation) of the alkene (to sp³ carbons), but also perhaps show where the large additional bend energy originates in the less stable conformers, particularly the large dihedral alkene angles and the deviance from 120^o for the carbonyl bond angle.

Reactivity of Bridgehead Alkenes: What is a Hyperstable Alkene?

The emergence of so-called hyperstable alkenes, alkenes that, despite appearing in strained (often ring) conformations, actually show less torsional strain the the parent hydrocarbon, ie the alkane equivalent and hence have decreased reactivity due to increased stability. Such examples are found in bridgehead alkenes where the parent hydrocarbon is perhaps less suited to the particular geometry imposed by the rigidity of the rest of the molecule. For example, it has been found that cyclohexane groups near the bridgehead systems can often control the overall geometry by demanding a chair conformation and, as such, the conformers (right) are orientated to show these chairs, and how the rest of the molecule may "suffer" as a consequence. These can infact dictate which alkene is formed when, for example, a dehydrobromination is performed. The most stable alkene not only conforms to the normal stability of alkenes based on substitution orders, but also on how an adjacent cyclohexyl group can orientate itself. An example from the literature is shown, right, using Allinger's MM1 forcefields and the concept lends itself greatly to molecular mechanics, as it focuses on its strengths, van der Waals and torsion in the geometry.

The same paper introduces a term called "Olefin Strain" which will be explored here. It refers to the stability of the parent hydrocarbon relative to the alkene. This will be relevant here in addressing the decreased reactivity that was observed when trying to derivatise the alkene in the taxol intermediate introduced above. The "Olefin Strain" is negative when the alkene is actually preferred to the sp³ hydribidised analogue, ie the geometry of the alkene is favoured relative to the hydrogenated version. To explore that statement, the torsional energy will be calculated for the hydrogenated product of the taxol intermediate , which is shown here in the low energy analogue of the alkene with the same chair geometry.

Example of Chair Dominated Alkene Formation

Relative Energies of the Taxol Intermediate and its Parent Hydrocarbon (product of hydrogenation)

Energy in (kcal/mol)
	Alkene (relative to Alkene)	Alkane (relative to Alkene)
Stretch	2.568 (0)	2.6414 (0.0734)
Bend	10.7789 (0)	11.6659 (0.8870)
Stretch-Bend	0.3226 (0)	0.5681 (0.2455)
Torsion	19.6035 (0)	22.7071 (3.1036)
Non-1,4 VDW	-1.3575 (0)	-1.9135 (-0.5560)
1,4 VDW	12.5499 (0)	15.1488 (2.5989)
Dipole/Dipole	-0.1834 (0)	0 (0.1834)
Total Energy	44.282 (0)	50.8179 (6.5359)

Whilst energy comparisons for calculations by the same method (here MM2) are best saved for isomers and conformations, they are also said to be applicable to simplistic reactions, such as the hydrogenation calculated here. The alkene has a lower energy overall (not a readily comparable figure, different number of atoms and hence energy terms), but of more interest is the fairly large quantitative increase in torsion, ie strain, of the system. (The alkene torsion is lower by 3.1 kcal/mol.) A major contributor to this energy might be the rather eclipsed conformation here; . The dihedral angle is only 27^o, but would be 60^o ideally. This is excellent evidence for supporting the hyperstable alkene theory, and is consistent with the observation that this alkene is slow to react. Further the van der Waals figure is rather higher for the alkane. This is attributable to the transannular close H-H contact of ~1.96 Å, whilst it is much larger for the alkene - the alkene carbons are supposed to be eclipsed due to the sp² hybridisation. The heats of formation were also calculated using the PM6 semi-empirical method, and the difference may be considered the heat of hydrogenation. The hydrogenated product shows a decrease in heat of formation of 23.98 kcal/mol (alkene - alkane = -65.701 - -89.055 kcal/mol), decreasing the stability of the product. Finally, the alkane, using the Visualise button immediately above the table, shows an internal sp³ angle of 119^o, unfavourable for an alkane (109.5^o ideal), but near ideal for an alkene.

The hydrogenation product of the atropisomer in which the CO is up has a high energy of 58.3129 kcal/mol so was not considered. Also, this product would be harder to make as the starting atropisomer is less stable.

---

Use of Semi-Empirical Calculations to Predict Reactivity and Estimate Spectra

A Chloro-Diene

HOMO of the Diene - the alkene on the left has a much greater electron density

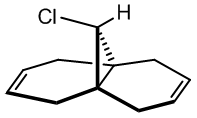
Predicting the Relative Reactivities of Non-Equivalent Double Bonds

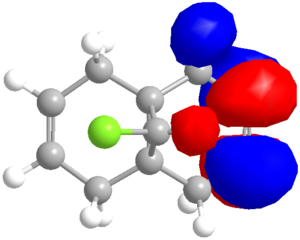
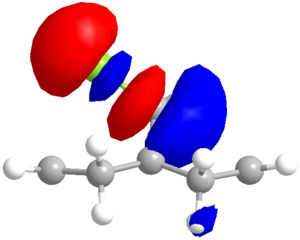
Semi-empirical calculations, which can be applied by methods such as the PM6 method already encountered, or the RM1 method, calculate molecular orbitals by applying quantum mechanical wavefunction treatments. This is particularly useful for considering the reactivity of simple molecules that have more than one possible nucleophilic or electrophilic group. Which is more reactive? A simple approach is applied to the diene (9-chloro-1,4,5,8-tetrahydro-4a,8a-methanonaphthalene) shown to calculate the relative reactivity of each alkene. The molecule is first optimised using the MM2 forcefield to decrease the calculation time of the PM6 calculations, which are run to produce the molecular orbitals, with the HOMO the focus of attention, as this is likely to be the reactive species that would, for example, attack an electrophile. The preliminary result is shown in the orbital image (right), clearly indicating a high electron density on the alkene which the chlorine substituent is directed toward (syn or endo).

When epoxidised with m-CPBA, the reported data quotes a 78% yield of product with mono-epoxidation (on the lower face) of the endo alkene - in full agreement with the prediction based on orbital density of the HOMO (and the bottom being the more open face). The exo alkene is found to favour reaction onto the top face:bottom face in a 2:1 ratio, probably due to the lower face position of the first epoxide. This reaction is a side product of the epoxidation, and is seen only when the endo alkene is also epoxidised, constituting a 6:94 ratio of by-product to product, showing remarkable regiospecificity. It is noted that the slightly less reactive HOMO-1 has large orbital density on the exo alkene.

Having discerned that the experimental data is well predicted by the modelling, rationalisation of the effects chemically can be done with confidence. There are a few additional clues as to the chemistry at work. Firstly, as shown via the Chloro-Diene button, the distance between the bridgehead carbon to either of the double bond carbons on either side of the molecule (see diagram) is not even, with the exo double bond closer by ~0.22Å (lit. 0.24Å). This bias suggests an attractive interaction on the exo side, and examination of the LUMO+1 suggests a π_C=C → σ*_C-Cl (anti-periplanar) stabilisation of the exo double bond, decreasing its nucleophilicity significantly. However, one must not leap to conclusions without considering all the options. Clicking the Mono_alkene button shows that even without the exo double bond, there is a distance bias. This can now be also, at least partially, attributed to an electrostatic repulsion between the endo double bond and the chlorine atom; see a spacefill representation of the repulsion: .

Considering the Quality of the Molecular Orbitals

Looking closely at the molecular orbitals produced by PM6, deviations from the expected (C_s) symmetrical distribution are seen. This is clearly not correct, so the PM6 orbitals cannot be taken too seriously (due to a known coding error in the program). Switching the calculation method to RM1 gave symmetrical orbitals, but the data was less comparable to the literature, as shown in the table below. Despite the lack of symmetry, the PM6 model appears to give a better optimised geometry. The PM3 method was also used, and was able to reproduce the images from the literature, but the optimised geometry was considerably different, with the Cl atom exerting a much greater repulsion of the endo double bond, which is forced below the plane of the bridgehead . The deviance from the distances (as shown in the table below) are also wayward.

Numbered Carbons for Distance Measurements

Distances between the bridgehead carbon and one of the carbons on the double bond (on each side of the bridgehead); see above Jmol button applet for example

distances/Å	C(11)-C(2)	C(11)-C(8)	Difference
X-ray	3.243	3	0.243
PM6	3.2688	3.0498	0.2190
RM1	3.0860	2.9170	0.1690
PM3	3.4506	3.0411	0.4095

Therefore a compromise must be reached. It would appear that the PM6 method is producing more sensible orbital shapes and geometry (in terms of explaining the experimental data) but the symmetry aspect is concerning. PM3 seems inconsistent with MM2, PM6 and RM1, which roughly agree with each other so will not be used further. RM1 produces sensible looking orbitals that are adept at explaining the observed reactivity, but that distort the geometry slightly. A comparison of the methods' orbitals is shown below.

Comparing the Molecular Orbitals Produced by Different Calculation Methods

Method	HOMO-1	HOMO	LUMO	LUMO+1
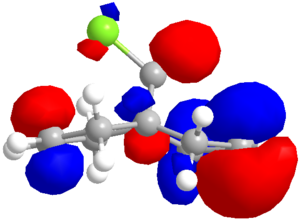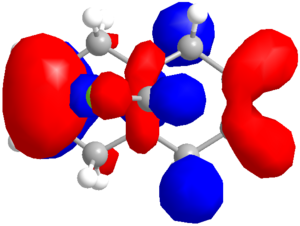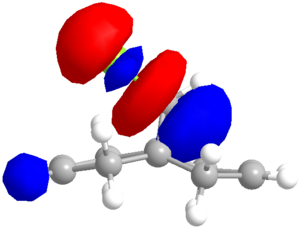PM6		Sideview of the PM6 HOMO
RM1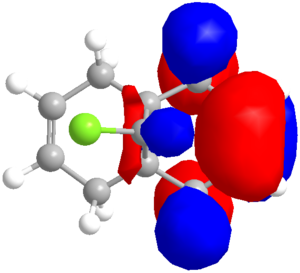

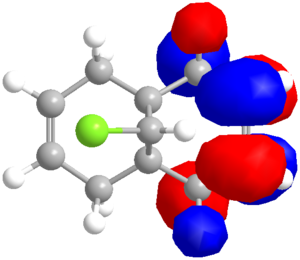A clear difference between the methods is the σ*_C-Cl, which is the LUMO for RM1 but LUMO+1 for PM6. (Using PM3 it is reported to be the LUMO+2.) The LUMO and LUMO+1 are reversed for the two methods. The HOMOs are roughly the same, but RM1 has no density on the exo carbon, whilst PM6 has a small amount on the upper face of the alkene. The RM1 data will have to be concluded to be more reliable for the orbitals, but this exercise shows that there is room for improvement in both calculation methods.

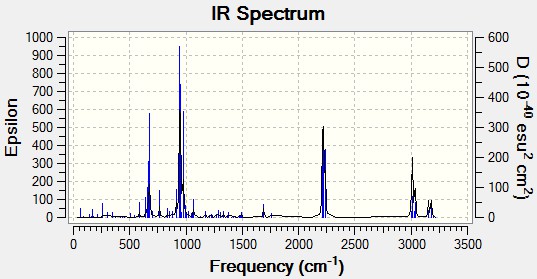
IR Frequency Estimates of Various Double Bond Environments

Gaussian was used to calculate/estimate the IR spectra of the alkene described above, which is compared to calculated data for several analogues, including the Mono_Alkene described above as well as several substituted alkenes.

An Example IR Spectrum - the SiH₃ Alkene

Wavenumbers for the Estimated IR Stretches of Some Substituted Alkenes: (refer to each column for the definition of X-Y in each case)

(stretches)	Diene	Monoalkene	HC=C-BH2	HC=C-CN	HC=C-OH	H2C-C=O	HC=C-SiH3
energy in (cm-1)
C-Cl	770.90	779.93	759.04	765.79	766.78	771.85	763.82
syn/endo C=C	1757.36	1753.76	1756.55	1756.54	1756.28	1754.94	1756.24
anti/exo C=C	1737.09	N/A	1657.21	1706.31	1776.60	N/A	1690.32
X-Y (sym)	3178.72	3174.92	(BH2) 2593.05	(CN) 2340.06	(OH) 3821.33	(C=O) 1812.02	(SiH3) 2218.59, 2234.8
X-Y (asym)	3156.60	3152.31	(BH2) 2665.9	N/A	N/A	N/A	(SiH3) 2214.56
XC=C-H Str	N/A	N/A	3165.00	3188.93	3192.85	(s) 3043.96 (as) 3100.00	3152.82
Cypropyl-H	3197.15	3213.71	3190.81	3190.49	3196.04	3195.32	3195.58

The salient features of the table will be commented upon. Firstly, the major differences between each molecule are clearly the double bond stretches of the exo (substituted) alkene. BH₂, as a Lewis Acid, can accept density from the π_C=C, weakening the bond and predicting a lowered stretching energy (as wavenumbers are directly proportional to energy: $E=h\nu =hc$$\tilde{\nu }$). The HO-C=C is normally seen in its tautomeric ketone form, so this was also calculated, giving a surprisingly high CO stretch of 1812 cm^-1 (the program overestimates stretches compared to experimental data). The C=C double bond stretch with the hydroxyl substituent is rather high, at 1776.60 cm^-1, indicating that resonance is not weakening the bond via donation into the π*_C=C, but that the bond is strengthened - perhaps this additional density is being funnelled into the σ*_C-Cl orbital, though the C-Cl stretch is still quite large. The SiH₃ group results in a weaker C=C stretch at 1690.32 cm^-1, which may be rationalised by σ-conjugation from the SiH bonds. The electron withdrawing cyano group can withdraw electron density via resonance, and this results in the weaker double bond stretch (1706.31cm^-1) observed (relative to the free alkene).

More pertinent to the above argument, is the stronger C-Cl stretch for the monoalkene, indicating more electron density in the C-Cl bond compared to the diene. This supports the stabilising argument above, as the stretch will be weaker if some electron density is removed from this bond (π_C=C → σ*_C-Cl) which was suggested in the case of the diene.

Various illustrative heteroatom-H stretches are also included, and the interesting behaviour of the high energy cyclopropanyl proton stretch, which is hard to rationalise, though perhaps, the higher C-H frequency of the mono alkene than the diene is due to the increased electron density in the bond (less donation into the surrounding system from the π_C=C as discussed above).

It appears harder to rationalise all the C-Cl stretches. The BH₂ analogue has a much weaker C-Cl bond than the diene, indicating more double bond donation into the σ*. This is reflected in the weaker double bond stretching frequency (1657.21 cm^-1), which might also be partially donation to the empty boron p orbital. This holds. However, looking at the CN_alkene, the double bond stretch is weaker (possible donation into the CN group) but the C-Cl bond is also weaker (relative to the diene), which is the reverse of what is expected, so this cannot be the whole story.

This calculation may come down to relative stabilisations of the differing groups and a full MO diagram for each species may be necessary to rationalise the results. Alternatively, the modelling may not be accounting for all effects, distorting the results.

---

Mini-Project: Using Computer Modelling to Predict the Properties and Spectra of Tsitsikammamine A and a Regioisomer

Tsitsikammamine A

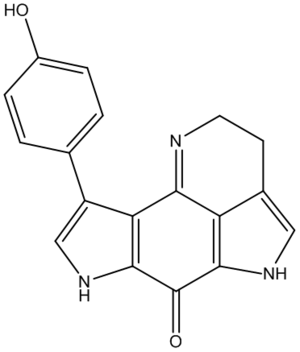
Outline

Regio Isomer of Tsitsikammamine A

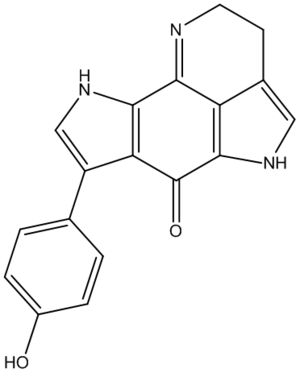
Tsitsikammamine A is described as a "bispyrroloiminoquinone alkaloid" by the discovers of the relatively recently isolated natural compound, extracted from a marine sponge in the Tsitsikamma Marine Reserve in 1996. It has more recently been tested in vitro for anti cancer activity. Its structure was determined based on ¹H and ¹³C NMR, IR and UV spectra, but no crystallographic data is reported. In 2009, the molecule was reported in a total synthesis paper (with further derivatives thereafter), which describes its synthesis and that of a close regioisomer, in which the phenol group at the C#3 position on the lefthand pyrrole is swapped with the pyrrole nitrogen, as a result of a non-specific reaction onto a 1,4-benzoquinone (shown later). Due to the restrictions on the type of molecule that can be used for the calculations, the direct products of this reaction were not used (not geometrically constrained enough - too many protecting groups). Instead, the final products (Tsitsikammamine A and isomer), both which follow an identical synthesis, are considered. The total synthesis paper reports very close ¹³C shifts compared to the original paper, and the results of the modelling show very good agreement in confirming the structure, and one incorrect assignment (though with minor consequences). The ¹³C-NMR estimates from computer modelling are also used to show how the two regioisomers of the synthesis can be distinguished, with the analysis based mainly on the relative shieldings of the carbonyl group carbons, which was the focus of a similar study.

Experimental

Tsitsikammamine A was drawn in Avogadro(MacOS), imported into ChemBio and its geometry optimised with MM2 (Total Energy = 46.1306 kcal/mol) and then PM6 (Heat of Formation = 16.029 kcal/mol). A Gaussian input file was saved, and optimised using the code # mpw1pw91/6-31g(d,p) opt(maxcycle=25). The resulting (optimised) checkpoint file was subjected to the code # mpw1pw91/6-31(d,p) NMR scrf(cpcm,solvent=dimethylsulfoxide). The same was done for the regioisomer (Total Energy = 46.1651 kcal/mol; Heat of Formation = 14.138 kcal/mol).

# b3lyp/6-31G(d,p) opt freq was used to calculate the IR spectra.

Optimised Tsitsikammamine A	Optimised Regioisomer	Optimised Tsitsikammamine with Phenol Orthogonal
Optimised Tsitsikammamine A	Regioisomer	Regioisomer

Results and Discussion

The ¹³C-NMR spectra were calculated and the results are listed along with the literature values and assignments below. The initial results showed promise, though it was noted that although the tetra ring system was constrained, the fluxionality was not modelled in the phenol ring system, which has free rotation about the adjoining bond that is not modelled in the NMR calculations. As a consequence, the seemingly identical carbon species in the two ortho or meta positions were not identical as would be expected ("Estimated NMR" column). To add a greater depth of analysis, the optimised structure was edited minimally using the dihedral driver on ChemBio3D, assuming the rest of the molecule to remain unchanged (on average) but with the phenol orientated exactly orthogonal to the flat tetra ring system (as shown in the Jmol above; column "PhOH orthog"). This allowed a much greater accuracy of the now almost equivalent phenol carbon environments. The three obtained literature values are listed and the C# assignments shown in the table. There appears to be a compromise in the phenol orientation in the original Tsitsikammamine A structure. A favourable N-H interaction (shown in the applet above) is almost the perfect 0.258 Å value reported - closer would be less favourable, but increase the planar conjugative overlap to the aromatic pyrrole ring system.

(A note on the table layout: the calculated carbon# labels have been converted to match the labels assigned in the literature (so the carbons aren't matched with the Jmol applet carbons, see instead the diagram). The values are ordered in decreasing order for the Calculated NMR values, with all other values reordered to match the initial carbon# labels. The literature assignments are shown as reported in "Discovery NMR", the original paper. The carbon environments were not specifically assigned in the Total Synth Paper. The ¹³C NMR paper quotes 168 ppm for carbon#19, but this appeared in all respects to be a typographical error (poorly correlated with the rest of their data) and this was corrected to 158 ppm for this analysis). The braket-ed values are included to show difference calculations as been done throughout the wiki thus far. Where necessary, bold values are used to signify the actual value of the cell.)

Carbon Numbering for Tsitsikammamine A

NMR Data for Tsitsikammamine A

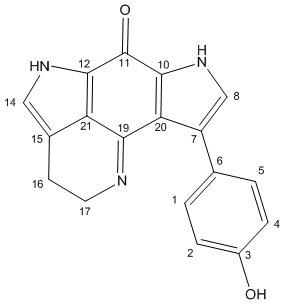
'Tsitsikammamine A'
	Calculated NMR	PhOH Orthog	Corrected/Correlated		Total Synth NMR	Discovery NMR	13C Analysis NMR
C#	ppm (relative to calc)	ppm (relative to calc)	ppm (relative Litsyn) (relative LitDiscovery)	Lit C#	ppm (relative to calc) (relative to orthog)	ppm (relative to calc) (relative to orthog)	ppm (relative to calc)
11	162.7 (0)	163 (0.3)	168.4 (-2.1) (-0.4)	11	166.3 (3.6) (3.3)	168 (5.3) (5)	172.5 (9.7)
19	153.8 (0)	153.7 (-0.2)	156.9 (0.7) (-1.9)	19	157.6 (3.8) (3.9)	155 (1.1) (1.3)	158 (4.2)
3	150.7 (0)	150.9 (0.2)	156.9 (0.7) (-0.2)	3	157.6 (6.9) (6.7)	156.7 (6) (5.8)
10	130.8 (0)	129.6 (-1.2)	135.2 (-0.6) (-1.4)	10	134.6 (3.8) (5)	133.8 (3) (4.2)
1	129.2 (0)	128.1 (-1.1)	128.1 (0.8) (2.1)	2or4	128.9 (-0.3) (0.8)	130.2 (1) (2.1)
5	126.4 (0)	129.8 (3.4)	129.8 (-0.9) (0.4)	2or4	128.9 (2.5) (-0.9)	130.2 (3.7) (0.4)
7	124.8 (0)	122.8 (-1.9)	122.8 (-0.4) (-0.6)	7	122.4 (-2.4) (-0.4)	122.2 (-2.6) (-0.6)
6	122.9 (0)	125 (2)	125 (2.2) (0.3)	6	127.2 (4.3) (2.2)	125.3 (2.3) (0.3)
12	121.7 (0)	121.5 (-0.2)	126.7 (1.1) (-1.2)	12	127.8 (6.1) (6.3)	125.5 (3.8) (4)
21	120.5 (0)	120 (-0.5)	120.5 (0.2) (1.3)	21	120.7 (0.2) (0.7)	121.8 (1.3) (1.8)
20	120 (0)	123.1 (3.1)	120 (-6.5) (-4.9)	20	113.5 (-6.5) (-9.6)	115.1 (-4.9) (-8)
8	118.4 (0)	121.3 (2.9)	123.6 (1.4) (-0.1)	8	125 (6.6) (3.7)	123.5 (5.1) (2.2)
14	117.2 (0)	117.3 (0.1)	122.4 (0.7) (0.1)	14	123.1 (5.9) (5.8)	122.5 (5.3) (5.2)
15	117.1 (0)	117 (-0.1)	117.1 (2.1) (1)	15	119.2 (2.1) (2.2)	118.1 (1.1) (1.1)
4	111 (0)	110.8 (-0.1)	110.8 (5.4) (4.3)	1or5	116.2 (5.2) (5.4)	115.1 (4.1) (4.3)
2	110.1 (0)	109.9 (-0.2)	109.9 (6.3) (5.2)	1or5	116.2 (6.1) (6.3)	115.1 (5) (5.2)
17	51.8 (0)	51.6 (-0.2)	51.8 (-6.8) (-2.7)	17	45 (-6.8) (-6.6)	49.1 (-2.7) (-2.5)
16	20.8 (0)	20.6 (-0.2)	20.8 (-3.2) (-2.4)	16	17.6 (-3.2) (-3)	18.4 (-2.4) (-2.2)

Correction of the Raw Data

• The calculated carbonyl carbon (#11) varies by 3.3 ppm, 5ppm or 9.7 ppm depending on the literature value used to compare it. Carbonyls often need corrective values applied of about 0.96δ + 12.2 ppm. This takes the calculated CO carbon up to 168.4 ppm, now with a difference of 2.1, 0.4 or -4.1 ppm respectively, a much better fit.
• Similarly, the imine, the nitrogen analogue of the carbonyl, can be corrected analogously changing the original error of (3.8, 1.1 or 4.2 ppm) to (2.2, 4.8 or 1.8 ppm) respectively; representing a slight overall closer value. An excellent fit can be obtained by correcting by 0.94δ + 12.2 ppm (minimised using Excel's Solver function) giving a calculated value of 156.9 ppm, representing an error of only (-0.7, 1.9 or -1.1 ppm) respectively.
• It was found that correcting all carbons connected to a nitrogen atom (with an effective double bond; pyrrole is aromatic) with the above correction made the data sit a lot better compared to the literature data and it seems very reasonable to that this is a correct analysis.
• If the phenol hydroxyl based carbon is corrected using the same correction of the carbonyl (a fair assumption), the accuracy is improved from and error of (6.9 and 6.0 ppm) to (0.7 and -0.2 ppm).
• The two meta (relative to OH) phenol carbons #1 and #5 are a better match if the orthogonal data is used, so these are included in the table. To be consistent, the para carbons are also swapped, but these are still significantly erroneous (~5 ppm off on each occasion).

Confirmation of the Assigned Structure

The third possible isomer

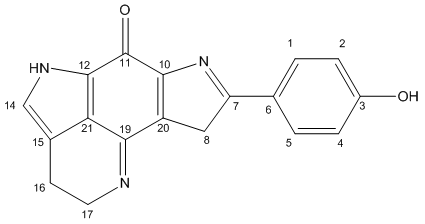
The calculated (corrected) NMR values are in good agreement with the literature values to the extent that the structure is very likely to have been assigned correctly. Many of the largest errors can be accounted for by the above corrections, and are listed in the Corrected/Correlated column. There are two slightly larger errors remaining. Firstly, C#1 and C#5 are ~5 ppm too low. (It is noted first that the literature assigned the ortho and meta carbons the incorrect way around.) It has already been mentioned that the phenol is the main cause of inconsistency in the calculations due to the lack of fluxionality in the calculations and it is possible that this leads to the poor values, even though the orthogonal data is little changed compared to the original data for these shifts. The second poor value is for C#20. The calculated values are in this case too high, so the corrections applied above increase the error. The calculated value (120.5 ppm) is very similar to the value for C#21 (120.0 ppm), which is reasonable given the pseudo symmetry of the molecule (ignoring the phenol). Therefore the error is likely to be in the α-phenol orientation, which is poorly modelled in the calculations. The error might also be attributed to an incorrect structure, but the only reasonable change would be to move the phenol group to C#8. This model was made and tested, but can be discounted, because the NMR predicts C#7 (where the phenol is in Tsitsikammamine A) to occur at a shift of 100.4 ppm, and the corresponding literature value would be 123.5 ppm. There is no other shift close enough to be considered an incorrectly assigned peak either. Again, conformationally, the phenol is not planar, with three key attractive interactions marked on the Jmol Visualisation.

Comparing Regioisomers

Numbered Regioisomer

NMR Data for the Regioisomer of Tsitsikammamine A

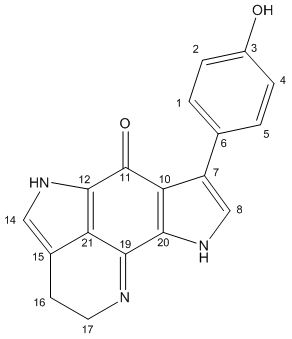
'Tsitsikammamine A (regioisomer)'					'Tsitsikammamine A'
	Calculated NMR	Corrected/Correlated	Total Synth Lit	13C Lit		Corrected Tsitsikammamine A
C#	ppm	ppm (relative to LitTotal Syn) (relative to Lit13C)	ppm (relative to Calc)	ppm	C#	ppm (relative to corrected isomer)
11	170.5	175.9 (-1.4) (-1.2)	174.5 (4)	174.71	11	168.4 (-7.5)
3	150.8	150.8 (-0.2)	150.6 (-0.2)		19	156.9 (6.1)
19	148.9	155.1 (1.5) (1.6)	156.6 (7.7)	156.71	3	156.9 (1.8)
20	131.4	135.7 (-1.4)	134.3 (2.9)		10	135.2 (-0.5)
1	129.0	129 (1.4)	130.4 (1.4)		1	128.1 (-0.9)
5	126.6	129 (1.4)	130.4 (3.8)		5	129.8 (0.8)
7	126.2	126.2 (0.2)	126.4 (0.2)		7	122.8 (-3.4)
12	123.4	128.2 (1.3)	129.5 (6.1)		6	125 (-3.2)
6	122.5	122.5 (3.1)	125.6 (3.1)		12	126.7 (4.2)
10	118.6	118.6 (2.3)	120.9 (2.3)		21	120.5 (1.9)
21	117.1	117.1 (3.6)	120.7 (3.6)		20	120 (2.9)
8	116.7	121.9 (-2)	119.9 (3.2)		8	123.6 (1.7)
14	116.2	116.2 (-0.1)	116.1 (-0.1)		14	122.4 (6.2)
15	115.1	115.1 (-0.1)	115 (-0.1)		15	117.1 (2)
4	110.9	110.9 (-0.1)	110.8 (-0.1)		4	110.8 (-0.1)
2	110.1	110.1 (0.7)	110.8 (0.7)		2	109.9 (-0.2)
17	51.4	51.4 (-2.3)	49.1 (-2.3)		17	51.8 (0.4)
16	21.4	21.4 (-2.5)	18.9 (-2.5)		16	20.8 (-0.6)

The reaction pathway to the two regioisomers

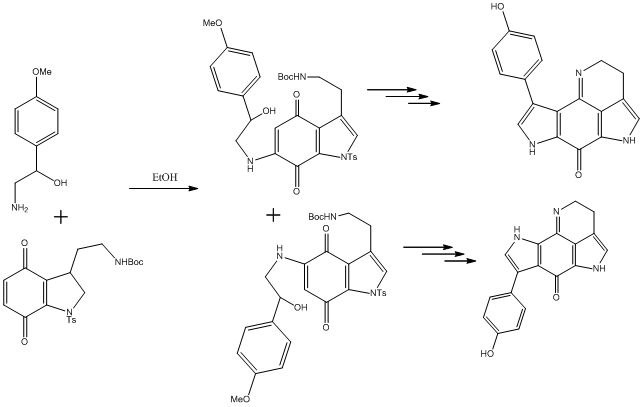
The reaction that leads to the regioisomer is shown and the regioisomer is pictured in the jmol applet section above. Similar corrections were applied to the carbonyl carbon and the imine; because the orthogonal spectrum was not run again, the erroneous phenol carbon shifts were corrected manually to match the highest of the two values, which is what was observed with the orthogonal molecule, to make the carbon shifts match (C#1 and C#5). However one anomaly arose. The shift for C#14, to which a correction was applied in the original molecule, was not applied to the isomer, because the value was already almost exactly in agreement. Additionally, the carbon shifts meta to the phenol hydroxyl group were, in the isomer, in excellent accord, which was not seen in the original molecule. It is possible that the program does not account for interactions over a certain distance away, therefore neglecting conjugative effects, which are clearly possible in this molecule. More specifically, the phenol is much closer to the dominating carbonyl group in the isomer, so perhaps the effects are better modelled in this case.

The key difference in the regioisomer shifts are the carbonyl carbon shift (C#11), whilst the imine shift appears less decisive. This sentiment was echoed in the aforementioned computational paper, in which ΔCO (ppm) was calculated for a range of quinone based structures.

Additional Data: IR Spectra

The original paper quoted 3 IR values found for Tsitsikammamine A. The IR data was calculated with the code quoted above. Due to the size of the molecule, the calculations took longer than some, and there were many modes in the output. These were difficult to compare, due to the error in the calculated stretch values (~8%). The ν_CO was calculated to be 1725.62 cm^-1 for Tsitsikammamine A, and 1721.53 cm^-1, which could be used to determine which isomer was present, if the error was consistent between the two calculations. The values are very close, and could easily be distorted due to the error and should therefore not be used definitively.

The values quoted in the literature were not assigned, which makes comparison to the data much more difficult than the NMR assignments. The values quoted were 1660, 1440 and 780 cm^-1. Experience (and the intensities of the calculated IR CO stretch) suggests that the 1660 cm^-1 should be the CO stretch, which is consistent with a quinone CO stretch. It is clear that this cannot be correlated to the calculated value, with the error being 3.8% (65.6 cm^-1). The other values are less assignable, due to the high number of C-N bonds in the pyrrole systems.

Due to the length of time required to run this calculation, the UV spectrum was not attempted. Additionally, the ¹H spectra are not included as they require incredible accuracy of the optimised structure; the phenol orientation is unconfirmed, there are few protons anyway, and nitrogen based protons are notoriously more difficult to predict.

Conclusion of the Mini Project

• Tsitsikammamine A, and two regioisomers were optimised to the mpw1pw91/6-31g(d,p) level using Gaussian and the ¹³C-NMR spectra calculated. After minor corrections, the data proved to be an excellent fit, and the two likely regioisomers were screened out, with the literature assigned structure very likely to be correct. The literature incorrectly assigned the two sets of equivalent phenol carbon shifts.
• The maximum shift difference after correction for the calculated Tsitsikammamine A NMR shifts was -6.5 ppm for C#20, although this is not representative of the average error of all other peaks of 1.2 ppm, [although this is not inclusive of the incorrect phenol carbon shifts (~6 ppm out), which are probably incorrect due to lack of a constrained geometry]. This argument may apply for the C#20 too, which is very close to the phenol. It would seem the optimised geometry is not entirely correct, and that the phenol ring would spend more time planar and conjugated, which may deshield C#20 further, improving the accuracy of the value. The model seemed to place more emphasis on the attractive N-H through space interaction.
• The regioisomer data was very well correlated to the literature values. The average error was only 1.4 ppm.
• The data can be used to assign regioisomers by considering just the differences CO carbon ppm shift, which is affected a lot due to the presence or absence of the pyrrole β-nitrogen.
• The IR data was not useful, due to the large molecule having many vibrations. The lack of accuracy of the IR stretches means the ν_CO cannot be used to assign regioisomers.
• The proton NMR was not useful due as it is not very accurate, particularly in distinguishing the few, similarly shifted protons in Tsitsikammamine A. Using the Karplus equation on the proton dihedral angles of a very planar molecule is of little benefit.
• Whilst computational techniques have been fairly successful for this molecule, it has been highlighted that the technique is fairly poorly where non-constrained geometry is concerned. However, the large size of the molecule here was fairly well modelled, despite extended conjugated systems, and it is predicted the modelling will be very precise in predicting small, very rigid ring systems.

Published Data

Tsitsikammamine A: NMR File: DOI:10042/to-7384 Tsitsikammamine A: IR File: DOI:10042/to-7444

Tsitsikammamine A Isomer: NMR File: DOI:10042/to-7386 Tsitsikammamine A Isomer: IR File: DOI:10042/to-7442

The IR output files gave the Sum of the Thermal and Electronic Free Energies to be = -1008.171244 E_H for the isomer and -1008.234047 E_H for Tsitsikammamine A.

---

References

Final edit Kga08 16:40, 4 March 2011 (UTC)