Rep:Mod:kc2009

Year 3 Computational Chemistry Lab - Transition States and Reactivity

Introduction and Method

This experiment aims to examine the transition states and the reactivity of the reactants and product in the Cope Rearrangement reaction and two Diels Alder cycloadditons. In the experiment, the lower level of theory of HF/3-12G were first measured (Hartreee-Fork = HF). The results were reoptimized to the B3LYP/6-31G level of theory using the density functional theory (DFT). This is to improve the efficient of calculation as it is computationally less expensive if the lower level of theory were first used to map the potential energy surfaces. The reactants and products were analysis in a different way from the transition states. Considering the reactants and products first. The molecules were optimized to a minimum using the low level of theory then the high level of theory and the results were easily obtained. However for the transition states, each fragments were individually optimized to a minimum and were then put together. The complete transition state state was then optimized to a TS(Berry) with the calculation of force constant. The results were then obtained. Other methods without the use of force constant was also tested. It was found for this experiment that it is computationally more efficient to optimize using the force constant method. From the optimized transition states, we could obtain the frequency of each individual bond and also predict the possible structure of the product. This first part could be done by doing a frequency calculation. The prediction was done using the Intrinsic Reaction Coordinate (IRC) method. A problem encountered for the IRC method was that the minimum could not be reached without a high number of points calculated. This was the computationally most expensive part of the experiment. It is also notable that the molecular orbitals could be visualized from the optimized molecules. Thus, the nature of the highest occupied molecular orbital (HOMO) and the lowest unoccupied molecular orbital (LUMO) could be observed and analysed. Note that in the following tables for bond length, unless specified, the bond referring is a C, C bond. Due to the error of the creation of JVOL compressed surface file script, .cub file could not be converted to JVXL files and the JSmol animations of the molecular orbitals could not be generated.

Nf710 (talk) 10:04, 19 November 2015 (UTC)A fairly standard intro you have some understanding of the concepts but you have-not shown any understanding of the theory.

Cope Rearrangement

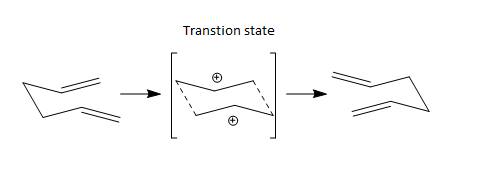
Cope Rearrangement is a very well known reaction where the [3,3]-sigmatropic rearrangement of 1,5-dienes occurs. This reaction was discovered and developed by Arthur C. Cope in early 20th century. In this experiment, 1,5-hexadiene were considered. The reaction scheme is shown in scheme 1.

Scheme 1 - Cope Rearrangement of 1,5-hexadiene

Nf710 (talk) 10:04, 19 November 2015 (UTC) You have got 2 carbo-cations in this intermediate. This is incorrect.

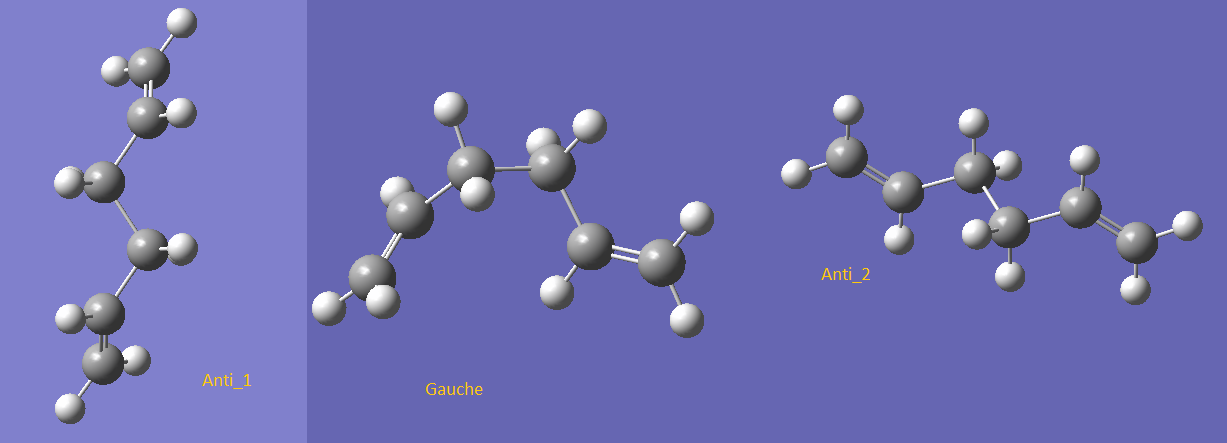
The reactant and the product of the reaction were first optimized using HF/3-21G. Since the reactant and the product would have the same variation of geometries, thus, they are analysed together. Two major groups of conformers were calculated and it was predicted that the anti-conformation would give the lower energy conformation over the gauche-conformation. Surprisingly, it was found that the lowest conformer is actually one of the gauche conformation. The HF/3-21G results of two anti-conformers and one gauche-conformer are shown below.

Figure 1 - Conformers (HF/3-21G)

JSmol animations of the conformers (HF/3-21G): Anti_1 Anti_2 Gauche

Table 1 - Results of most energetically stable confomers

Conformer	Anit_1	Anti_2	Gauche
Point Group	C2	Ci	C1
Energy (Hartrees)	-231.69260235	-231.69254	-231.69260235

The three conformers shown above are gauche-conformer of the lowest energy and the two lowest energy anti-conformers. Anti_2 was predicted to have the lowest energy. However when comparing the results, it could be observed that the gauche-conformer has the lowest energy with -231.69260235 hartrees. The energy were converted to kcal/mol using the fact that 1 hartree equals to 627.509 kcal/mol.The DFT assisted B3LYP/6-31G level optimized results are shown below.

Nf710 (talk) 10:10, 19 November 2015 (UTC) You haven't suggested why the anti would be lowest or why the gauche is actually lowest. You also havent specified which gauche you have done.

Figure 2 - Conformers (B3LYP/6-31G)

JSmol animations of the conformers (B3LYP/6-31G): Anti_1 Anti_2 Gauche

The geometry of the conformers were compared between different levels. The energies were not compared between different levels since the change of each conformer would be relative to each other. The bond angles and bond length of the molecule changes slightly after the change in level. However, the same point group were retained after the re-optimization of higher level. After the reactant and product has be analysis, the transition state optimization was carried out next. The following are the transtiion state optimized chair- and boat-like structures.

Nf710 (talk) 10:21, 19 November 2015 (UTC) You havent given any data here

Figure 3 - Chair-like and Boat-like Transition States

JSmol animations of the transition state chair and boat: Chair-like transition structureBoat-like transition structure

The chair-like transition state structure has an energy of -231.61932244 hartrees and C2h point group. The boat-like transitiion state structure has an energy of -231.60280248 hartrees and C2v point group. The chair-like transition state has a lower energy content ans is shown to be energetically more stable in these calculations. Although the chair-like transition state is energetically more stable this is not the transition state in this reaction. From the QST2 calculation, the boat transition state is re-optimized, from anti_2_, to be the structure below. The energy of this transition strucuture is -231.683002550 hartrees and has a point group of Cs. This structure is different from the one obtained using the force constant method. This was looked as a limitation of the QST2 method since the transition state has to be correctly illustrated in the QTS2 method. The guess structure of it is not actuate. The QST2 calculation did make a contribution to guessing the transition state since the chair transition structure could not complete the run. The real transition structure should be the boat-like structure for the anti conformers. The is supported by reference 2 which showed a similar result.

Figure 4 - QST2 Optimized Structure

JSmol animations of the QST2 Optimized Structure: QST2 Optimized Structure

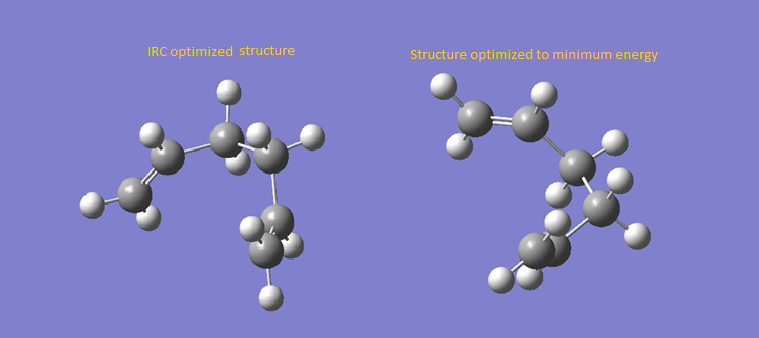
From each optimized transition state, IRC calculation could be further applied to look for their respective products. For instance, chair-like transition state has been considered. The IRC calculation has been done for the optimized chair-like transition state. It was found that the number of steps has yet to reach minimum. The last IRC optimized structure has been optimized itself to a minimum to give a predicted product. The product has an energy of -231.69166702 hartrees and has a C2 point group.

Figure 5 - Prediction of Product from Chair-like Transition State

JSmol animations of the predicted product of chair-like transition state: Predicted product

Nf710 (talk) 10:35, 19 November 2015 (UTC) This is a poorly written report. You havent checked a single imaginary frequency. Your jmols are your input files. you have barely given any data such as geometries or bond angles or theormo chemistry and you havent re optimised your transition structures and compared them to experiment.

Diels Alder Cycloaddition

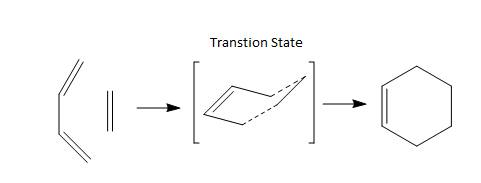
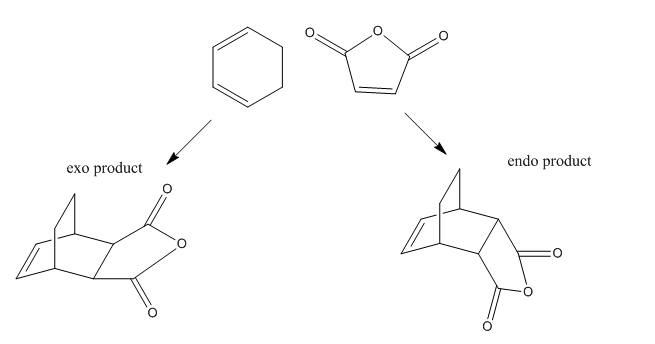
Two different cycloadditions were considered and they are shown in scheme 2 and 3. Scheme 2 shows the cycloaddition of an ethylene and butadiene. Scheme 3 shows the reaction of cyclohexa-1,3-diene with maleic anhydride. The study of scheme 2 is to look at the HOMO and LUMO of the transtion state of the transition state. The aim of the experiment of scheme 3 is to examine the regioselectivity of this Diels Alder reaction. It was stated by the endo rule that the endo product would be preferentially produced over the exo product. This experiment aims to show further evidence of this argument.

Scheme 2 - Diels Alder Cycloaddition of Ethylene and Butadiene

Scheme 3 - Diels Alder Cycloaddition of Cyclohexa-1,3-diene and Maleic Anhydride

The reaction in scheme 2 will be considered first. In this reaction, two different reactants were used and they are cis-butadiene and ethylene. The structure of each starting materials were individually optimized first and they are shown below.

Figure 6 - Structure, HOMO and LUMO of cis-butadiene

JSmol animations of the transition structure of cis-butadiene: Transition structure of ''cis''-butadiene

Figure 7 - Structure, HOMO and LUMO of ethylene

JSmol animations of the transition structure of ethylene: Transition structure of ethylene

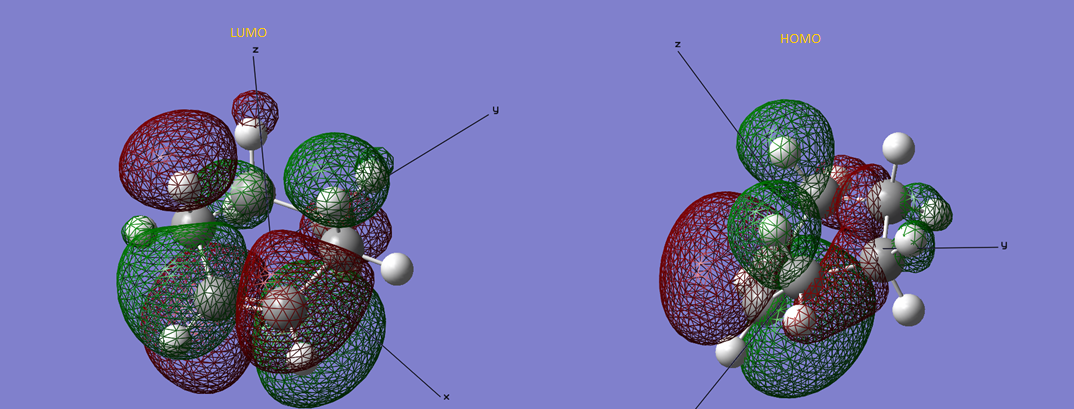
The energy, in hartrees, for cis-butadiene and ethylene are -154.05394316 and -77.60098811. The point group of cis-butadiene is C2v and that of ethylene is D2h. The HOMO and LUMO of the starting materials shows the reason for the reaction to occur. The LUMO of cis-butadiene and HOMO of ethylene could interact with each other and the HOMO of cis-butadiene could interact with the LUMO of ethylene due to the similarity of wavefunction. The 2 different interactions form two different bonding orbitals (i.e. the two new sigma bonds in the product). This result matches with reference 3. From figure 6 and 7, the molecular orbital were analysed. For cis-butadiene, its LUMO has 6 nodes and it is symmetrical along the xz plane. The HOMO of it, however, is asymmetrical and has 4 nodals. This part of the molecular orbital has a plane of reflection at the xz plane and the yz plane. For the ethylene, the LUMO is symmetrical in all three planes (xy, xz and yz) while the HOMO is only symmetrical in the yz and xz planes. 4 nodes are present for the LUMO and 1 node for HOMO.

(Nodes are regions where the electron density is 0. Therefore there are 1 and 2 nodes for the HOMO and LUMO of ethene respectively, and 2 and 3 for the HOMO and LUMO of cis-butadiene respectively Tam10 (talk) 17:41, 11 November 2015 (UTC))

Figure 8 - Transition State Structure Cyclohexene

JSmol animations of the transition state of first Diels Alder reaction: Transition state of first Diels Alder reaction

(This doesn't look like the correct transition state. Did you perform an IRC in both directions to confirm it? Tam10 (talk) 17:41, 11 November 2015 (UTC))

Figure 9 - HOMO and LUMO of Transition State of Cyclohexene

The transition state structure of cyclohexene were optimized and shown above. The energy of this transition structure is -231.72017266 hartrees with a C1 point group. From the HOMO and LUMO of cyclohexene, the nodal properties and symmetry are analysed. The LUMO is asymmetric but with a plane of reflection at the yz plane, it has 12 nodes. The HOMO is symmetric along the plane of yz and it has 8 nodes. From reference 5, the van der Waals' radius of carbon is 1.7 Å. Comparing this with the results in table 2, for both sp3 and sp2 bonds, it is shorter than the van der Waals' radius. The sp3 bond length ranges from 1.51 Å to 1.565 Å and sp2 bond is at around 1.32 Å. It has been found that the sp3 sigma bonds that are closer to the sp2 pi bond would be shorter than sp3 sigma bonds that are further away. Comparing this to the results of reference 4, the bond lengths has a very similar value. Considering the fact that trans-butadiene were optimized in the reference, it showed the bond length is more dependent for its neighboring nature of bonding than the geometry.

(This would be easier to see if you had the right TS. Even so, the orientation of the HOMO makes it difficult to tell what the symmetry is. The geometry isn't symmetric which doesn't help either Tam10 (talk) 17:41, 11 November 2015 (UTC))

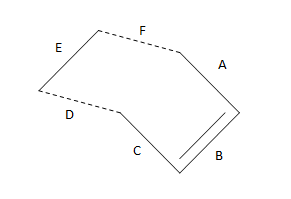
Figure 10 - Bond Length of Transition State of Cyclohexene

Table 2 - Bond Lengths of Transition Structure of Cyclohexene

Bond	A	B	C	D	E	F
Bond length (Å)	1.51389	1.31721	1.51381	1.56407	1.55424	1.54740
Hybridization	sp3	sp2	sp3	sp3	sp3	sp3

The reaction mechanism of the reaction were considered next. From the frequency calculations, the bond formation frequency and the lowest positive frequency were plot below. Looking at just the bond formation frequency, the two CH2 groups of the ethylene are vibrating in the same phases showing that the reaction should be synchronous. The motion of the bond formation frequency and the lowest positive frequency is similar but one of the terminal CH2 groups of cis-butadiene vibrates differently in lowest positive frequency. It is opposing the vibration of one of the CH2 groups of the ethylene.

(This doesn't seem to be reflected by what you have optimised. It's hard to tell what this TS separates but if it is bond-forming, it would be asynchronous (bonds forming one by one) in this case. However, the C-C distances are too short to be bond-forming Tam10 (talk) 17:41, 11 November 2015 (UTC))

Animation 1 - Vibration of bond formation (-93 Hz)

Animation 2 - Vibration of lowest positive frequency (224.8 Hz)

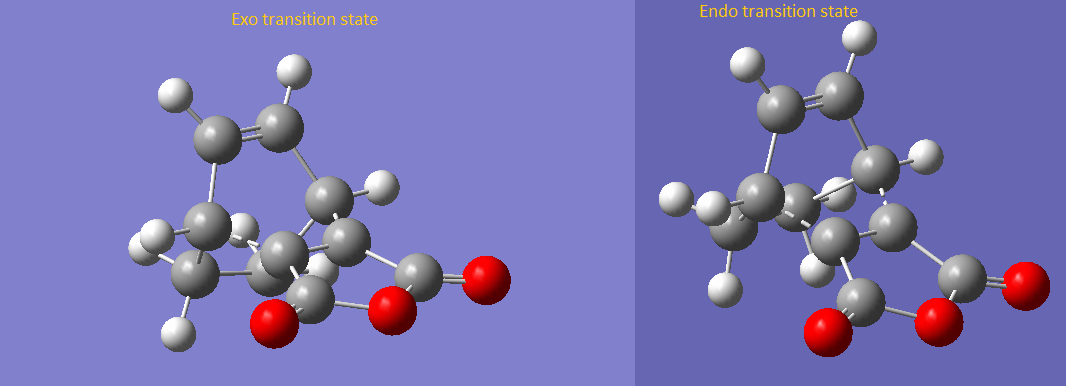
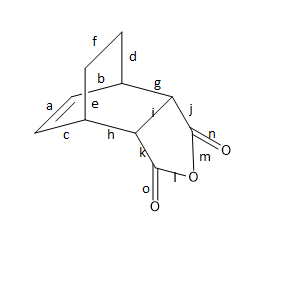
In this part, the reaction of scheme 3 was examined. The transition structure of endo- and exo-product were examined and listed below. The energy for the endo- and exo transition structures are -604.38676864 hartrees and -604.38674777 hartrees respectively. C1 point group were observed for both products. This shows that the endo-product is preferentially produced since the endo transition structure is energetically more stable than the exo transition structure. This supports with the endo-rule for Diels Alder reaction.

Figure 11 - Transition structure of endo- and exo-product

JSmol animations of the transition state of second Diels Alder reaction: Endo Transition State Exo Transition State

(These look pretty much like the same structure, and neither the endo nor the exo unfortunately Tam10 (talk) 17:41, 11 November 2015 (UTC))

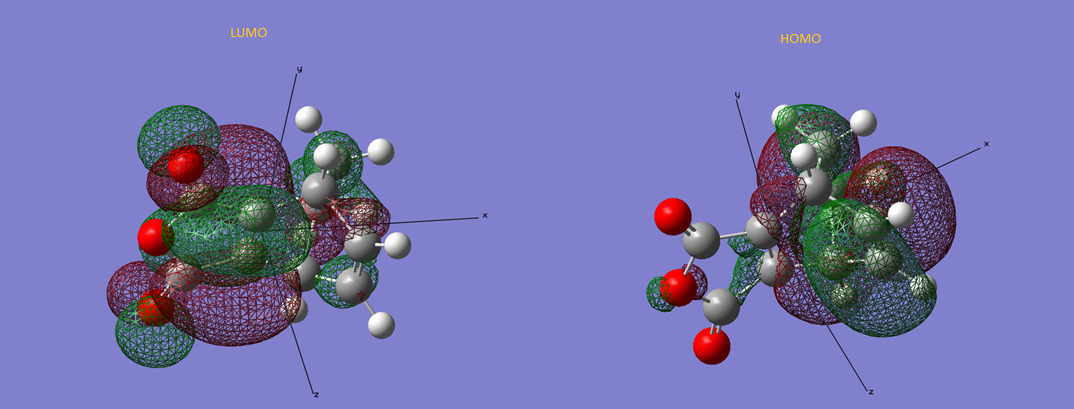
Figure 12 - LUMO and HOMO of Transition structure of exo-product

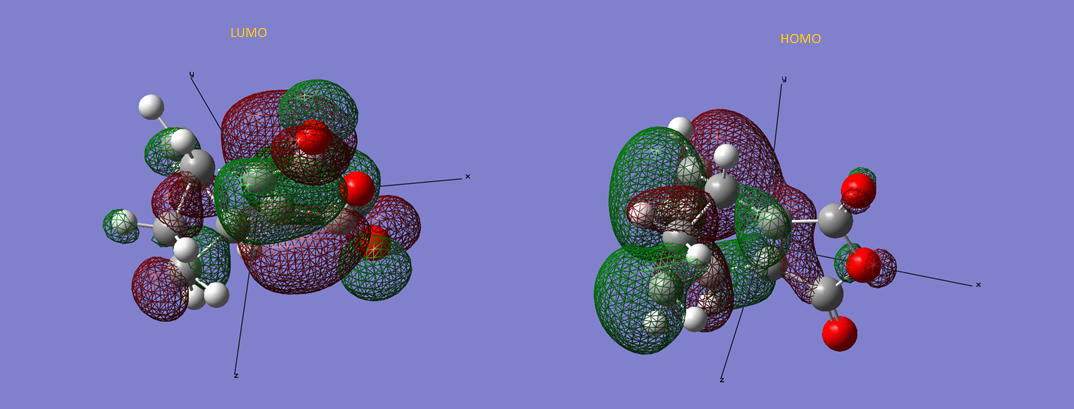
Figure 13 - LUMO and HOMO of Transition structure of endo-product

Looking at figure 12 and 13, the LUMO and HOMO of the two different products were examined. The HOMO for the exo product is asymmetrically and has 7 nodes while its LUMO has 18 nodes. The LUMO, although being asymmetrical as well, it has a point of reflection from the plane of xz. The endo product's LUMO is asymmetrical and has 16 nodes. It also has a plane of reflection along the xz plane. The HOMO of endo product is symmetrical along the xz plane and has 8 nodes. Secondary orbital overlap could be seen in the HOMO of the two transition structures. According to reference 6, in a pericyclic reaction, the secondary orbital overlap was stated to be a positive overlap of nonactive frame in the frontier molecular orbitals. From the HOMO of endo and exo product, it could be observed the nonactive oxygen groups is interacting with the frontier molecular orbitals. If we separate the transition structure in to two parts, the maleic anhydride and the others, it could be observed in the HOMO that the orbital interactions are much less significant in the maleic anhydride part when comparing with the other parts. This is the secondary orbital overlap in this case.

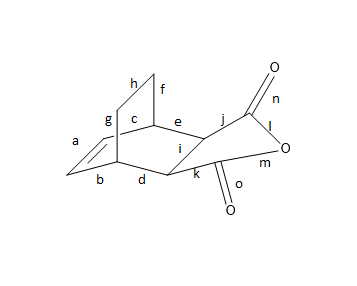
Figure 14 - Bond Length of Transition State of exo-product

Table 3 - Bond Lengths of Exo Transition Structure

Bond	a	b	c	d	e	f	g	h	i	j	k	l	m	n	o
Bond length (Å)	1.31654	1.58122	1.75652	1.48613	1.47735	1.50766	1.51957	1.59461	1.31487	1.47886	1.48358	1.40084	1.39792	1.18827	1.18800
Hybridization	sp2	sp3	sp3	sp3	sp3	sp3	sp3	sp3	sp3	sp3	sp3	sp3 (C-O)	sp3 (C-O)	sp2 (C=O)	sp2 (C=O)

Figure 15 - Bond Length of Transition State of endo-product

Table 4 - Bond Lengths of Endo Transition Structure

Bond	a	b	c	d	e	f	g	h	i	j	k	l	m	n	o
Bond length (Å)	1.31697	1.52019	1.51324	1.58059	1.75665	1.59270	1.48573	1.47123	1.31385	1.47830	1.48451	1.38742	1.40195	1.18819	1.18830
Hybridization	sp2	sp3	sp3	sp3	sp3	sp3	sp3	sp3	sp3	sp3	sp3	sp3 (C-O)	sp3 (C-O)	sp2 (C=O)	sp2 (C=O)

Looking at the results of table 3 and 4. It could be observed that the sp3 bonds has a greater variation than that of the previous Diels Alder reaction (see table 2). The sp3 bonds for exo and endo transition structures ranges from 1.31 Å o 1.76 Å. The sp2 bonds for both exo and endo transition structures are around 1.32 Å. It has been observed again in this part that when the sp3 bonds are located closer to groups of C, C double and carbonyl groups, the bond length would increase. This effect is more significant for C, C double bond groups than carbonyl groups.

References