Rep:Mod:kandyrocks1
Module 1 - Kandeeban Gopalakrishnan
Introduction
Technology has evolved throughout the last few decades and with that, computational chemistry is no exception to this rule. Gone are the days where the structure and properties of compounds were predicted by ‘wet’ experiments. Instead, the use of computational chemistry provided scientists with a simple yet effective tool to accurately calculate the structure and properties of various molecules and solids. However, one must bear in mind that various approximations are used to obtain results; although computational chemistry is not an exact science, it has now reached a level where results from computer-simulated experiments essentially match those provided by experimental means. In this module, the total energy of molecules will be predicted using three different computational methods: molecular mechanics, density functional methods and semi-empirical methods.
Molecular mechanics is employed as a means to study small and large molecules alike (it was only until recently that methods other than molecular mechanics were used to determine the energy of large molecules). This method involved the use of a mathematical model where the atoms in the molecule are held together by use of springs. The total energy of the molecule is determined by a number of factors such as bond stretching, non-bonding interactions and dihedral anglesCite error: Invalid parameter in <ref> tag. This method omits the use of electrons but instead relies heavily upon the Born-Oppenheimer approximation. An advantage of using this method is that the calculation of heat of formation and strain energy is approximately the same as of that observed experimentally. It is also a very quick and cheap method to use, making it a popular tool for chemists.
Density Functional theory involves the study of the electronic structure of molecules. Here, exchange and correlation interactions have been computed into the model, allowing for accurate data to be obtained. The low cost associated with this computational method makes it a viable and attractive option for molecular studies.
Semi-empirical methods involve the usage of many approximations derived from experimental observations. Although this method generates results at a rapid rate, results can vary in terms of accuracy and very few properties can be predicted reliably. A large advantage gained from this method is that parameters such as geometry and heat of formation can be obtained as a result from this methodCite error: Invalid parameter in <ref> tag. Furthermore, this method successfully describes Organic Chemistry.
All three methods will be tested in this module to see how well the results match up with those obtained from literature.
Dimerisation of Cyclopentadiene
Dicyclopentadiene is used in a variety of applications, ranging from high-energy fuels to the use of the compound as a co-polymer in the polymerisation of ethylene.
The dimerization of cyclopentadiene occurs readily at room temperature, (typically over a period of a few hours) resulting in the formation of dicyclopentadiene dimer via the Diels-Alders reaction. This dimer readily reverts back to the monomer form, via retro -Diels-Alders reaction, when heated to higher temperatures (typically around 180oc) as it is more entropically favourable for this process to occur.
The dimerisation of cyclopentadiene is illustrated below (figure 1).
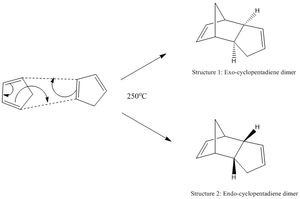
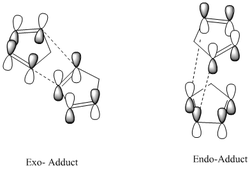
In this stereospecific [4+2] concerted reaction, the diene and the dienophile are able to approach each other in two specific orientations, allowing for two different stereochemical outcomes to be attained. This alignment is illustrated in figure 2.
For quite a number of years, the dominant formation of the more sterically-hindered endo product was an enigma to any scientists. However, with the use of MO theory, Woodward et al[1] were able to rationalise this experimental observation. It was deduced that there was greater p- orbital overlap in endo products, compared to the exo-produts, thus leading to a more stable product.
The reaction is driven to completion by the formation of two newly-formed C-C bonds which join both rings together (2 C-C σ bonds are formed in place of 2 C-C π bonds). The energy released from this reaction is approximately 40kJmol-1. An additional factor behind cyclopentadiene’s preference to dimerise is that the molecule exists as a fixed s-cis conformer (resulting in larger steric strain), allowing for a rapid reaction to occur.
| Product 1 (exo-product): Jmol | Product 2 (endo-product): Jmol | |
| Stretch | 1.2851 | 1.2501 |
| Bend | 20.5811 | 20.8503 |
| Stretch - Bend | -0.8379 | -0.8357 |
| Torsion | 7.6559 | 9.5105 |
| Non-1,4-Van Der Waals | -1.4179 | -1.5436 |
| Van Der Waals | 4.2326 | 4.3185 |
| Dipole Dipole | 0.3775 | 0.4475 |
| Total Energy (kcalmol -1) | 31.8765 | 33.9975 |
As shown in table 1, these values were calculated using the ChemBio3D program. After the molecule was successfully drawn, MM2 was used whereby the molecule was minimised in energy to obtain the lowest energy (stable) conformation. The values obtained for each property was tabulated.
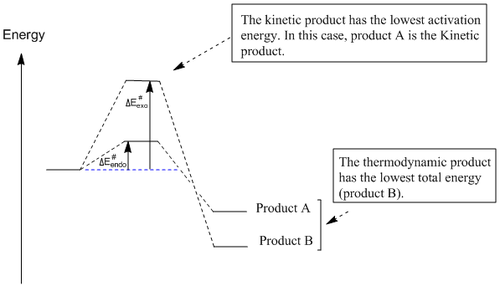
By comparing the endo and exo isomer, it can be seen that the exo isomer is lower in energy (ca. 2.1Jmol-1) than the endo isomer. This difference in energy is due to the 1,4-strain experienced by the endo isomer (this is indicated by a large difference in the torsion energy component). As the exo isomer has a lower total energy, it confirms that this isomer is the thermodynamic product while the endo isomer is the kinetic product for this reaction
Endo and Exo
Hydrogenation of dicyclopentadiene
The hydrogenation of the cyclopentadiene dimer results in the formation of two possible products (see figure 4). Both products will be examined to explore the ease of hydrogenation on both C=C double bonds.
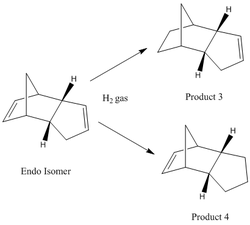
Analysis of both isomers (using MM2 force field option) shows that product 3 is lower in energy (ca. 4.5kcalmol -1), and therefore more thermodynamically stable, than product 4. Furthermore, this large difference in energy Is largely due to the bending energy component of both molecules. The bending energy component of product 3 is 5.3kcalmol -1 lower than that of product 4. The optimum bond angle for sp2 hybridised Carbon bonds is 120°. Ideally, upon a geometrical change from sp2 to sp3 hybridisation, an optical bond angle of 109°C is attained. When the double bond in the bridgehead is reduced (to form product 3), a new bond angle of 108° is obtained. When the other C=C double bond is reduced (to form product 4), a 113°C bond angle is achieved. There is less ring strain (ca.4°) in the former product and, as mentioned earlier, this determines why product 3 is the thermodynamic product of this reaction.
| Product 3: Jmol | Product 4: Jmol | |
| Stretch | 1.0957 | 1.2771 |
| Bend | 14.5193 | 19.8664 |
| Stretch - Bend | -0.5493 | -0.8346 |
| Torsion | 12.4985 | 10.8068 |
| Non-1,4-Van Der Waals | -1.0667 | -1.2257 |
| Van Der Waals | 4.5139 | 5.6330 |
| Dipole Dipole | 0.1406 | 0.1621 |
| Total Energy (kcalmol -1) | 31.1521 | 35.6850 |
The Synthesis of Taxol
Introduction
Taxol is often the subject of interest from scientists, especially due to its significance in the medical field. Upon discovery of this molecule in the late 1960’s, Taxol has been a key component of most Ovarian cancer treatments[2]. This section will focus on the two key intermediates, as proposed by Paquette, which utilises the atropisomerism concept. This type of isomerism occurs when the high energy barrier to rotation prevents rotation about a single bond; as a result, different conformers are attained. In most cases, such conformers can be separated using various methods such as selective crystallisation. However, at higher temperatures, it may be hard to different between these isomers as their structure converge together.
The Intermediates
For this part of the module, the MM2 and MFF94 force fields were used to calculate the total energies of the different Taxol intermediates. Even though both of these models will be used, values cannot be compared as both models rely on a different set of approximations and parameters. MMFF94 force-field is a useful tool in this calculation as it was built with the exact purpose of dealing with larger molecules eg. complex drug molecules and proteins etc... As such, it gives the user an advantage when trying to calculate the total energy of the Taxol intermediates. Upon manipulating the geometry of the Taxol intermediates several times, it was concluded that there were a minimum of three different conformers for each product: twist-boat, chair and chair’ conformer.
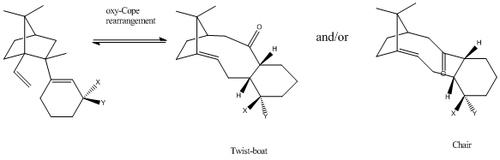
| Product 9 | Product 10 | |||||
| Twist-boat | Chair | Chair\' | Twist-boat | Chair | Chair\' | |
| Stretch | 2.7119 | 2.6205 | 2.7299 | 2.8770 | 2.5517 | 2.9166 |
| Bend | 11.7412 | 11.3391 | 15.8436 | 17.2774 | 11.3780 | 16.2348 |
| Stretch - Bend | 0.3237 | 0.3437 | 0.4732 | 0.344 | 0.3205 | 0.4628 |
| Torsion | 21.8640 | 19.6627 | 18.3422 | 20.6076 | 17.3629 | 19.8443 |
| Non - 1, 4 VDW | -2.0944 | -2.1531 | -1.0845 | -0.8947 | -2.2655 | -0.5980 |
| 1, 4 VDW | 13.9187 | 12.8725 | 13.1500 | 14.3778 | 12.7423 | 13.3152 |
| Dipole/ Dipole | -2.0316 | -2.0023 | -1.8284 | -1.7084 | -1.6998 | -1.6710 |
| Total Energy (kcalmol -1) | 46.4335 | 42.6831 | 47.4703 | 53.010 | 40.3901 | 50.5047 |
| MMFF94 Total Energy (kcalmol -1) | 66.4301 | 60.571 | 69.2952 | 77.9376 | 60.648 | 74.6264 |
From the results obtained, it can be seen that,in most cases, the chair conformers are lower in energy with respect to the twist-boat conformer. The chair conformers are arranged so that the Hydrogen atoms are staggered, hence, avoid steric clashing. However, the Hydrogen atoms in the twist-boat conformer are held in an eclipsed configuration thereby causing steric clashing to increase. This causes the molecule to destabilize to a small degree. However, the chair' conformer (Product 9 - Carbonyl down) is higher in energy than the twist-boat conformer. From the data analysis, one can see that the bend strain contributes a lot to this. Furthermore, it appears that on average, the conformers of Product 9 (carbonyl down) are 5.64kcal/mol more stable than their product 10 (carbonyl up) counterparts. Once again, this difference in energy is largely due to the angle strain; it appears that when the carbonyl moiety is facing upwards (above the plane), it experiences a greater degree of steric clashing, possibly with the carbon bridgehead.In addition to this, the two methyl groups attached to the bridgehead may provide additional steric strain to the molecule (as they clash further with the carbonyl moiety).
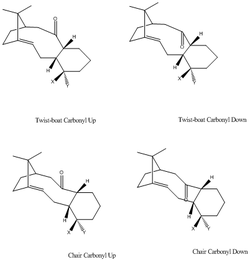
Hydrogenation of Taxol Intermediate
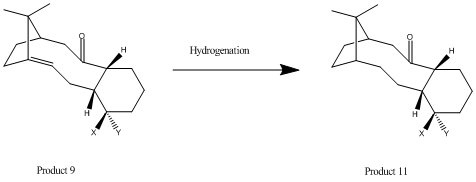
| Product 9 product): Jmol | Product 11 (Hydrogenated product): Jmol | |
| Stretch | 2.5517 | 3.0233 |
| Bend | 11.3780 | 15.1965 |
| Stretch - Bend | 0.3205 | 0.5868 |
| Torsion | 17.3629 | 21.6022 |
| Non-1,4-Van Der Waals | -2.2655 | -1.4901 |
| Van Der Waals | 12.7423 | 15.6113 |
| Dipole Dipole | -1.6998 | -1.7302 |
| Total Energy (kcalmol -1) | 40.3901 | 52.7997 |
Both isomers of Product 9 are part of a select group of hyper-stable bridgehead olefins (i.e. alkenes that possess negative olefin strain energies). Although it is expected for small double bonds to be relatively unstable (in the bridgehead form) due to the large bend-strain, it has been determined that larger polycyclic systems are fairly stable in this form (as strain energy affects these systems to a lesser extent than their parent hydrocarbon counterpart. This concept of ‘olefin strain’ is backed by the calculation run using the MM2 force-field. As shown in the table above, the hydrogenated product is higher in energy than its predecessor largely due to the increase in bend strain (and torsion). The angle-strain increases upon the hybridisation change from sp2 (123°, optimum ~122°) to sp3 (119°, optimum angle~109°. As such, this reasoning helps to explain why Taxol intermediates such as Product 12 undergo hydrogenation very slowly[3].
DFT and Semi Empirical MO Theory
Dichlorocarbene
In this part of the module, the semi-empirical method will be utilised in order to obtain an accurate prediction of the reactivity of molecules. This approach is known as ‘semi-empirical’ as the method incorporates the use of theoretical approximations with experimental observations. In this case, we will examine the reactivity of 9-chloro-1,4,5,8-tetrahydro-4a,8a-methanonaphthalene (product 12) in the presence of dichlorocarbene (electrophile). As reported by Halton, Boese and Rzepa,[4], Product 12 reacts regiospecifically with dichlorocarbene at the double bond which is situated endo to the chlorine atom.

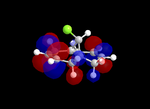
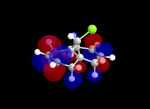
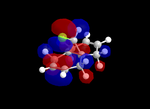
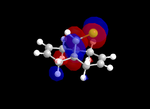
Molecular Orbitals
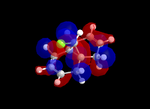
| Table 5: Illustration of the Frontier Orbitals of Product 12 | |||||||
| RM1(MOPAC) |  |
 |
 |
 |
 |
 | |
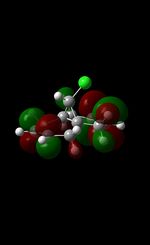
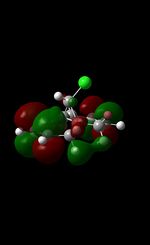
| Gaussview | 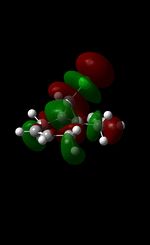 |
 |
 |
 |
 |
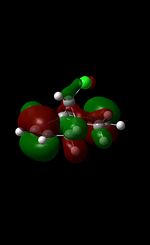 | |
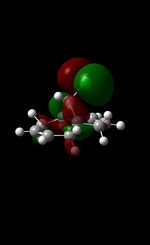
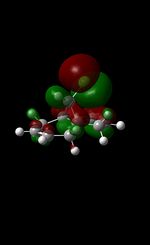
The MM2 force-field was applied to product 12 in order to optimise the geometry of the molecule. In addition to this, the MOPAC/RM1 MO method was used to obtain a representation of the molecular orbitals of Product 12.Initially, the MOPAC/PM6 MO method was used but no success was achieved using this method. Although the RM1 method was then used, the MO’s obtained did not exhibit a large degree of symmetry. RM1 reveals the existence of a bug within the program and hence, as a result of this problem, Gaussian was used (using the DFT method) in order to get a better illustration of Product 12’s molecular orbitals. As shown in the HOMO, most of the electron distribution is located next to the chlorine group and the alkene group situated endo to the halogen atom. Intrinsically, this tells us that this alkene group is much more nucleophilic compared to the other alkene group (endo to the H atom); the chlorine atom induces geometric distortion by causing the whole molecule to twist. In particular, the C-Cl σ* exo π orbital interactions causes the bridgehead and the exo-alkene double bond to move towards each other. Essentially, this will result in an increase in the nucleophilicity of the endo-alkene double bond (making it more reactive to dichlorocarbene). Another explanation for this increase in nucleophilicity, as proposed by Hehre, may be due to the ‘large sterically accessible π orbital area’[5] exhibited by the endo-alkene (as opposed to the exo-alkene). However, one should note that there is some small preference for the exo-product in terms of the ‘Cie-plak’ type effect[6]but this is not enough to override the endo-preference indicated previously.
IR Spectra
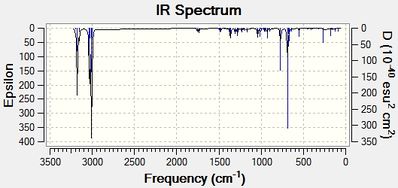 |
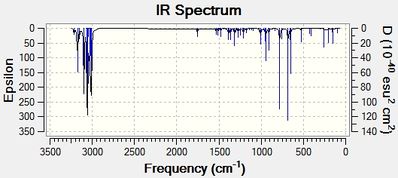 |
Upon hydrogenation of Product 12, the bond order of the C-Cl bond stretch increases by approximately 11cm-1. It should be stated that the C-Cl bond in the dialkene is weaker than its monoalkene equivalent as the exo-alkene donates electron density into the low lying C-Cl π*orbital (see MO diagram below[7]). With the removal of this interaction, the C-Cl bond becomes shorter upon hydrogenation of Product 12. In the IR spectrum for the dialkene, it can be noted that the peak at 1757cm-1 is the endo-alkene stretch while the peak at 1737cm-1 is due to the exo-alkene. By looking at the IR spectrum of the monoalkene, it can be seen that there is a peak missing in the 1737cm-1 region, thus confirming the identities of the peaks.
Glycosidation
Introduction
Fischer glycosidation is a thermodynamically controlled reaction which operates under equilibrium. In order to allow such a reaction to reach near-completion, one must use excess alcoholic reagent. Although (glycoside) isomers are formed in this reaction, the α-glycoside predominantly forms due to the anomeric effect.This effect arises when the lone pair on the ring’s oxygen atom is donated into the C-O σ* orbital (hyperconjugation).
However, stereo-chemistry can be controlled to a certain extent by the Neighbouring Group Effect[8] (NGP). In the Fischer glycosidation reaction, once the departure of the leaving group (at the α-position) occurs, a cyclisation reaction occurs between the carbonyl of the β-acetate group and the α-carbon; the oxocarbenium ion (cationic intermediate) returns to its cyclic hemiacetal form. As the large protecting group only allows nucleophiles to attack from the opposite side, the stereo-chemistry is controlled to a large extent i.e. the control of formation of α- or β-anomer depends on the positioning of this acetate protecting group (either above or below the plane). The overall mechanism is shown below:
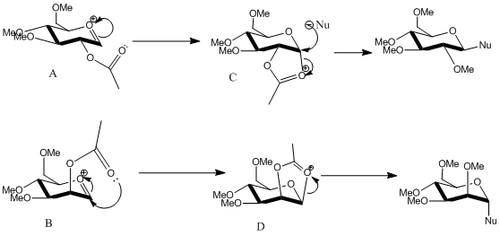
The MM2 force field and the MOPAC/PM6 program will be used to predict the likely stereochemistry of the intermediates and the products in this reaction (R=Me was used in this calculation to save computing time). The results have been tabulated below:
| A | A\' | B | B\' | C | C\' | D | D\' | |
| Stretch | 2.8896 | 2.3563 | 2.6969 | 2.3335 | 2.1355 | 2.8089 | 1.9736 | 2.6537 |
| Bend | 11.5823 | 9.8162 | 9.9869 | 14.6229 | 14.4423 | 17.6150 | 16.0933 | 17.1460 |
| Stretch - Bend | 1.0902 | 0.8992 | 0.99354 | 0.9975 | 0.7838 | 0.8205 | 0.8468 | 0.7699 |
| Torsion | 3.5980 | 1.2439 | 2.9370 | 1.6555 | 9.2080 | 8.0634 | 8.4385 | 8.2093 |
| Non - 1, 4 Van Der Waals | 1.0125 | -2.4305 | 0.0554 | -3.2689 | -2.2756 | -2.2410 | -3.3977 | -2.5525 |
| 1, 4 VDW | 18.8095 | 18.7207 | 19.3915 | 18.9052 | 17.5919 | 19.2486 | 17.1561 | 19.2469 |
| Charge/ Dipole | -19.9818 | -2.9151 | -21.6405 | -3.5871 | -9.3900 | 1.7260 | 2.1808 | -3.0634 |
| Dipole/ Dipole | 5.8695 | 3.7242 | 5.8944 | 6.3283 | -1.8962 | -1.9234 | -0.4928 | -0.7857 |
| Total Energy (kcalmol -1) | 24.8698 | 31.4148 | 20.2569 | 37.9869 | 30.5999 | 46.1180 | 42.7986 | 41.6251 |
| MMFF94 Total Energy (kcalmol -1) | -91.6562 | -77.0978 | -88.529 | -63.45017 | -91.655 | -66.8433 | -84.57731 | -65.497 |
Structure A and structure B differ as both have their respective acetyl protecting groups orientated in a different way. In the case of A, the acetyl group is orientated above the plane (allowing the nucleophile to attack from below the plane) while for B, the acetyl protecting group is orientated above the plane (thereby allowing attack from above the plane). Structure A leads to the formation of the β-anomer while structure B leads to the α-anomer as a result of NGP (as discussed above). By undergoing ring-flipping of structures A and B, A’ and B’ are formed respectively. All the original structures (A, B, C and D) are much lower in energy compared to their ring-flipped counterpart (A’, B’, C’ and D’). As you can see from the results, there is a very high barrier to structural conversion (ca.20kcal/mol in each case).
The total energies of structure A and C vary when using the MM2 force field option. However, upon using the MOPAC/PM6 model, it can be seen that the heat of formation for both structures are nearly identical (ca. -91.66 kcal/mol) as both structures are nearly identical to the ‘real/hybrid’ structure. The same reasoning holds for structures B and D. While both have different MM2 energies, they both have a very similar MOPAC value (-88.53 kcal/mol and -84.58 kcal/mol for B and D respectively. Furthermore, A’ and C’ are not identical in terms of enthalpy of formation value, due to the poor alignment by the nucleophile [as it has chosen the wrong angle to approach the electrophile (i.e. no at the Burgi-Dunitz angle~109.5º)]. This is not the case for structure A. The variations in energy between the MM2 and PM6 models occur as the MM2 model cannot form new bonds whereas the PM6 model can.
The total energies of structure A and C vary when using the MM2 force field option. However, upon using MOPAC/PM6 model, it can be seen that the heat of formation for both structures are nearly identical (ca. -91.66 kcal/mol) as both structures are nearly identical to the ‘real’ structure. The same reasoning holds for structures B and D. While both have different MM2 energies, they both have a very similar MOPAC value (-88.53 kcal/mol and -84.58 kcal/mol for B and D respectively. The variations between MM2 and PM6 occur as the MM2 model cannot form new bonds whereas the PM6 model can.
Mini Project:The selectivity between Wolff Rearrangement and 2-Alkoxy-2H-azirine using catalysts
Introduction
Hetero-cyclic compounds containing Nitrogen atoms such as Pyrroles have been of great interest to chemists and with that, there has also been a large amount of interest in the synthesis methods used. One novel way of synthesising pyrroles is the formation and subsequent rearrangement reaction of 2H-Aziridines. Although the formation of Aziridines looks unfavourable at first glance due to the high ring strain and large steric crowding associated with such a compound, they have been successively synthesised (in good yield) and this has been recorded by Padwa et al. However, one must take care with such compounds as they are prone to further reaction and subsequent decomposition. Furthermore, this molecule is very reactive as it can function as an electrophile and a nucleophile. This mini-project will focus on the work carried out by Jiang, Chan and Park[9]. This experiment focuses on the formation of two different isomer products: 2H-azirine-2-carboxylic esters and 2H-azirin-2-yl-2-methylpropan-1-one. The aim of this experiment is to use various metal catalysts in order to synthesise the 2H-azirine-2-carboxylic ester product exclusively.
In this mini-project, experimental and computational methods will be applied to confirm the structural properties of a known compound. In this case, the project will focus on the formation of two isomers; the reaction scheme has been provided below (figure 13). NMR and IR spectral data will be computationally calculated and compared to experimental literature values in order to assess how similar these values are to each other.
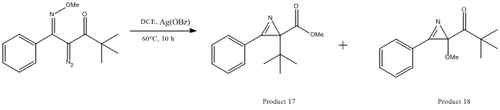
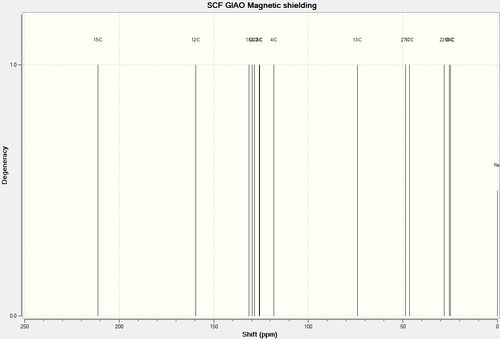
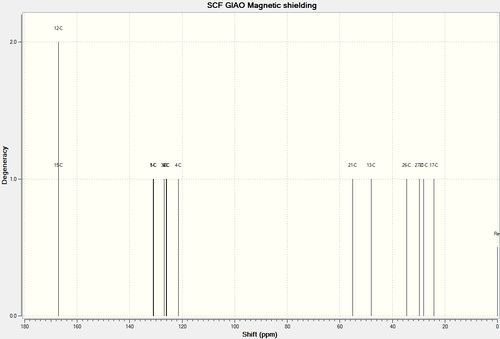 |
|
 |
 |
 |
|
 |
 |
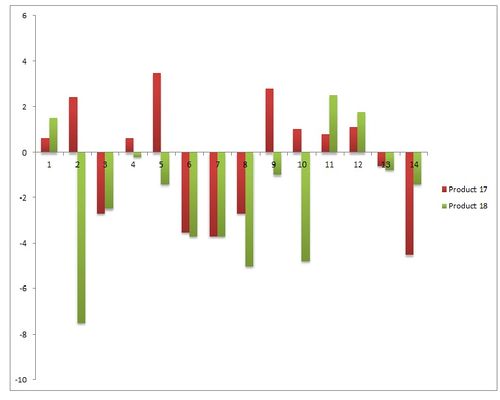
From both NMR spectrum, it is evident that there are a few features that can be used to distinguish between both product isomers. Product 17 can be distinguished by the two peaks present at 172.31 ppm and 166.76ppm. These peaks correspond to the carbonyl carbon atom and the chiral carbon atom respectively. Product 18 does not display these peaks but instead displays peaks at 211.20ppm and 159.41ppm. These sets of values correspond to the presence of the Carbonyl carbon atom and the carbon double bonded to the Nitrogen atom.
In the case of Product 17, the carbonyl carbon atom is more up-field (compared to the carbon atom in Product 18) as the entire carboxylic acid moiety experiences the resonance effect (and hence provides the Carbon atom with additional stability).
For both sets of results, the results obtained from Gaussian are very similar to the literature values, give or take 5ppm. As a result, it confirms the reliability of such computational methods.
IR Spectra
This section of the project will explore the extent to which both isomers can be distinguished from each other using IR spectroscopy. Also, as the spectra for both isomer products could not be found from literature, these spectrum will be compared to very similar compounds (see below).
| Figure 21: IR spectrum of Methyl 2-tert-butyl-3-phenyl-2H-azirine-2-carboxylate | Figure 22: IR spectrum of 1-(2-methoxy-3-phenyl-2H-azirin-2-yl)-2,2-dimethylpropan-1-one |
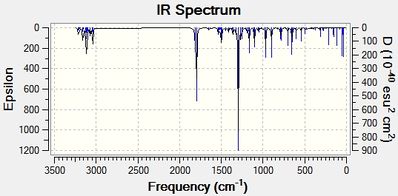 |
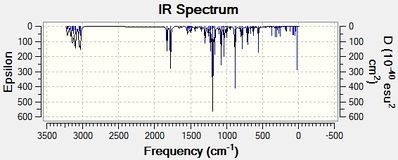 |
There is no literature IR spectrum present for product 17, however, a spectrum of a very similar product (Product 19[10] - methyl 3-phenyl -2H- azirine-2-carboxylate) will be used to identify the compound. Generally, most stretches that arise from Product 17 IR spectrum should arise in the Product 19 spectrum. However, the only difference between both molecules is that Product 17 has a t-Bu group attached to the chiral centre while the Product 19 has a Hydrogen atom attached there instead.
| Lit. Value(cm-1) | Gaussian calculated value (cm-1) | Deviation (cm-1) | peak assignment |
|---|---|---|---|
| 3000 | 2990.00 | 10 | C-H stretch (aromatic and aliphatic) |
| 1814.68 | 1777.01 | 37 | C=N imine stretch |
| 1797.77 | 1769 | 29 | C=O carbonyl stretch |
| 1597 | 1632.87 | 36 | C=C aromatic stretch |
| 1489 | 1491.84 | 3 | C - H bend |
| 1303 | 1297.03 | 6 | C-C sp3 stretch |
| 1274 | 1271.42 | 3 | C-O stretch |
| 793 | 789.99 | 3 | Aromatic Ring Torsion mode |
After inspection of the calculated results and the literature result, it can be seen that the values are fairly similar. However, two sets of values (carbonyl stretch and the aromatic C=C stretch) are out by ~40cm-1. As both molecules are very slightly different, the difference in stretch values can be neglected.
For the same reason, a compound similar to Product 18 was searched for in order to confirm the reliability of the IR spectrum generated. However, a suitable (and comparable) IR spectrum could not be found.
| Product 17(cm-1) | Product 18 (cm-1) | Deviation (cm-1) | peak assignment |
|---|---|---|---|
| 2990.00 | 2900.12 | 2 | C-H stretch (aromatic and aliphatic) |
| 1814.68 | 1826.56 | -12 | C=N imine stretch |
| 1797.77 | 1777.01 | 21 | C=O carbonyl stretch |
| 1632.87 | 1634.42 | -2 | C=C aromatic stretch |
| 1491.84 | 1492.03 | -0.2 | C - H bend |
| 1297.03 | 1252.29 | 45 | C-C sp3 stretch |
| 1271.42 | 1230.33 | 41 | C-O stretch |
| 789.99 | 781.84 | 3 | Aromatic Ring Torsion mode |
The table above represents the IR data obtained from both isomer products. In addition to this, we can see that there are two sets of peaks that are quite distinguishable from each other. Both the sp3 CH3 C-C stretch and the C-O stretch are useful indicators when differentiating between products.
In the case of the C-C stretch, this stretch involves the chiral carbon atom. Furthermore, if the OMe group is attached to it (Product 18), the OMe group may donate electron density to the carbon atom, causing a shift in the C-C stretch.
In the case of the other stretch (C-O), the C-O stretch in Product 17 (carboxylate product) will have a higher wavenumber (and bond strength) compared to its Product 18 counterpart. This is because there is additional resonance in the carboxylic acid moiety which causes greater stability and stronger C-O bonds [i.e. the carbonyl bond order decreases from 2 to 1.5 while the C-OMe bond order increases from 1 to 1.5 - this is stronger than the bond order (of 1) experienced by the C-OMe in Product 18].
Although these two differences in IR values are good indicators of the different isomers, IR analysis doesn't hold the same strength as NMR analysis.
Conclusion
From analysing the calculated values, it can be said that the computationally-generated NMR calculations mirrored the experimental literature values. This high degree of accuracy confirms that computational chemistry is an important asset to chemists. In addition to this, a comparison of the IR spectras shows us the accuracy of the computationally generated IR results when compared to the literature counterpart. Furthermore, it was established that IR analysis is a useful tool when trying to differentiate between both isomer products.
References
- ↑ Stereochemistry of Electrocyclic Reactions R. B. Woodward,Roald Hoffmann J.Am.Chem.Soc.;1965; 87(2); 395-397. doi:10.1021/ja01080a054
- ↑ Paquette, L.; Elmore, S. W.; Tetrahedron Letters, 1991, 319-322.
- ↑ Wilhelm F. Maier, Paul Von Rague Schleyer, J. Am. Chem. Soc., 1981, 103, 1891. DOI: 10.1021/ja00398a003
- ↑ Halton B.; Boese R.; and Rzepa H.S.; J. Chem. Soc., Perkin Trans. 2, 1992, 447-448
- ↑ Chao, J. Baker, W. J. Hehre and S. D. Kahn, Pure. Appl. Chem., 1991,63,283
- ↑ D. Hahn and W. J. Hehre, J. Am. Chem. SOC1.,9 87,109,663: 1988,110,4625
- ↑ Professor H.Rzepa, 2nd Year Conformational Analysis Module; http://www.ch.ic.ac.uk/local/organic/conf/
- ↑ March, J;Advanced Organic Chemistry: Reactions, Mechanisms and Structure’, Wiley-VCH, 2001, pp 404.
- ↑ Jiang, Chan, and Park, Expedient Synthesis of Highly Substituted Pyrroles via Tandem Rearrangement of α-Diazo Oxime Ethers, dx.doi.org/10.1021/ja300552c | J. Am. Chem. Soc
- ↑ http://riodb01.ibase.aist.go.jp/sdbs/cgi-bin/direct_frame_top.cgi





