Rep:Mod:jz12018
NH3 Molecules
Optimisation
N-H bond distance = 1.02Å
H-N-H bond angle = 106°
| Calculation Method | RB3LYP |
| Basis Set | 6-31G(d,p) |
| E(RB3LYP) | -56.55776873 au |
| Point Group | C3V |
Item Value Threshold Converged? Maximum Force 0.000004 0.000450 YES RMS Force 0.000004 0.000300 YES Maximum Displacement 0.000072 0.001800 YES RMS Displacement 0.000035 0.001200 YES
Ammonia Molecule |
The optimisation file is linked to here
Vibrational Analysis
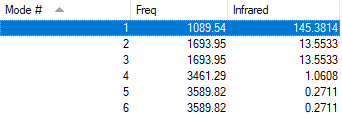
| Wavenum /cm-1 | Symmetry | Intensity /arbitrary units | Image |
| 1090 | A1 | 145 |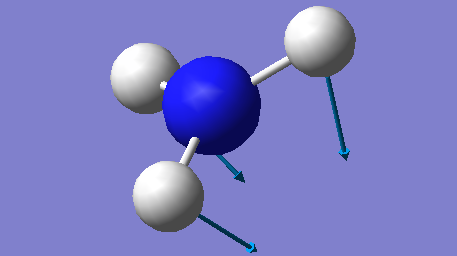 
|
| 1694 | E | 14 |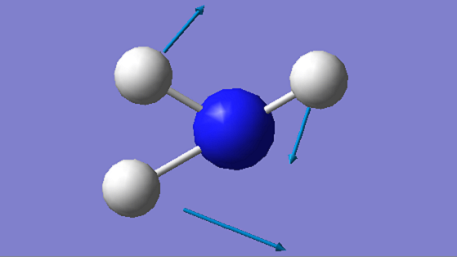 
|
| 1694 | E | 14 | 
|
| 3461 | A1 | 1 | 
|
| 3590 | E | 0 | 
|
| 3590 | E | 0 | 
|
Since NH3 molecules are non-linear, 6 modes of vibration are expected using the 3N-6 rule. As shown in the table, there are two degenerate modes at 1694 cm-1 and two other at 3590 cm-1, hence there are only 4 modes of different energies. As the vibration modes at 3590 cm-1 show 0 intensity, only 3 bands will be observed in an experimental spectrum of gaseous NH3.
The mode at 1090 cm-1 and the two degenerate modes at 1694 cm-1 are the bending modes and they have much lower energies compared to the other three stretching modes. The stretching mode at 3461 cm-1 is highly symmetrical, while the mode at 1090 cm-1 is often known as the "umbrella" mode.
Charge Analysis
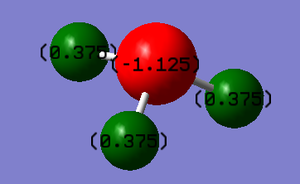
Relative charge on N atom is -1.125 and relative charge on each H atom is +0.375.
This is within my expectation because in NH3 molecules, N atom is more electronegative than H atom, hence N atom should be negatively charged and H atoms should be positively charged.
N2 Molecules
Optimisation
N-N bond distance = 1.11Å
| Calculation Method | RB3LYP |
| Basis Set | 6-31G(d,p) |
| E(RB3LYP) | -109.52412868 au |
| Point Group | D∞h |
Item Value Threshold Converged? Maximum Force 0.000000 0.000450 YES RMS Force 0.000000 0.000300 YES Maximum Displacement 0.000000 0.001800 YES RMS Displacement 0.000000 0.001200 YES
Nitrogen Molecule |
The optimisation file is linked to here
Vibrational Analysis
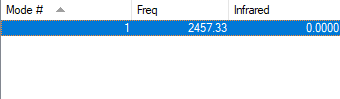
| Wavenumber /cm-1 | Symmetry | Intensity /arbitrary units | Image |
| 2457 | SGG | 0 | 
|
There is only one mode of vibration for nitrogen molecules and it is at 2457 cm-1.
This mode is a symmetric stretching mode, hence no bands should be observed in an experimental spectrum for gaseous nitrogen as this stretching mode involves no overall change in dipole moment.
Charge Analysis
Relative charge on both N atoms are 0.000.
This is within my expectation because in N2 molecules, the two N atoms are identical. The two N atoms should not have any relative charges since N2 is a homonuclear diatomic.
Comparison of N≡N bond length in optimised N2 and in Transition Metal Complex
One example of a mono-metallic transition metal complex that coordinates N2 is a structure with refcode YEQTIY. (link to the structureː https://www.ccdc.cam.ac.uk/structures/Search?Ccdcid=YEQTIY&DatabaseToSearch=Published)
The N≡N bond distance of an optimised N2 molecule is 1.11Å, whereas the N≡N bond distance in this metal complex is 1.12Å. The N≡N bond length in the experimentally determined crystal structure is 0.01Å longer than that of the computed N2 molecule. This is because nitrogen donates lone pair of electrons to bond with the electron deficient transition metal atom when acting as a ligand, causing the electron density to share among 2 N atoms and the transition metal atom. This means the electron density between the two N atoms in the ligand is less than an isolated N molecule, which effectively leads to weaker N≡N bond and larger bond distance in the ligand.
H2 Molecules
Optimisation
H-H bond distance = 0.74Å
| Calculation Method | RB3LYP |
| Basis Set | 6-31G(d,p) |
| E(RB3LYP) | -1.17853936 au |
| Point Group | D∞h |
Item Value Threshold Converged? Maximum Force 0.000039 0.000450 YES RMS Force 0.000039 0.000300 YES Maximum Displacement 0.000052 0.001800 YES RMS Displacement 0.000073 0.001200 YES
Hydrogen Molecule |
The optimisation file is linked to here
Vibrational Analysis
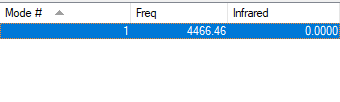
| Wavenumber /cm-1 | Symmetry | Intensity /arbitrary units | Image |
| 4466 | SGG | 0 | 
|
There is only one mode of vibration for hydrogen molecules and it is at 4466 cm-1.
This mode is a symmetric stretching mode, hence no bands should be observed in an experimental spectrum for gaseous hydrogen as this stretching mode involves no overall change in dipole moment.
Charge Analysis
Relative charge on both H atoms are 0.000.
This is within my expectation because in H2 molecules, the two H atoms are identical. The two H atoms should not have any relative charges since H2 is a homonuclear diatomic.
Comparison of H-H bond length in optimised H2 and in Transition Metal Complex
One example of a mono-metallic transition metal complex that coordinates H2 is a structure with refcode GUTQAN. (link to the structureː https://www.ccdc.cam.ac.uk/structures/Search?Ccdcid=GUTQAN&DatabaseToSearch=Published)
The H-H bond distance of an optimised H2 molecule is 0.74Å, whereas the H-H bond distance in this metal complex is 1.13Å. The H-H bond length in the experimentally determined crystal structure is 0.39Å longer than that of the computed H2 molecule. This is because in the crystal structure, both of the hydrogen atoms are bonded to the central transition metal atom, Ru, and a three-membered ring is formed. As Ru is electron deficient, both hydrogen atoms donate electron density to bond with Ru and to maintain the ring structure. The lower electron density between the two H atoms effectively weakens the H-H bond and the bond is lengthened as a result.
Energy Calculation of Haber-Bosch process
E(NH3) = -56.5577687 au
2 * E(NH3) = -113.1155374 au
E(N2) = -109.5241287 au
E(H2) = -1.1785394 au
3 * E(H2) = -3.5356182 au
ΔE = 2 * E(NH3) - [E(N2) + 3 * E(H2)] = -0.0557905 au
ΔE = -0.0557905 * 2625.5 = -146.5 kJ/mol
Negative ΔE suggests that this is an exothermic process, hence the product, ammonia gas, is more stable than the reactants.
HCN Molecules
Optimisation
C-H bond distance = 1.07Å
C≡N bond distance = 1.16Å
H-C≡N bond angle = 180°
| Calculation Method | RB3LYP |
| Basis Set | 6-31G(d,p) |
| E(RB3LYP) | -93.42458153 au |
| Point Group | C∞V |
Item Value Threshold Converged? Maximum Force 0.000044 0.000450 YES RMS Force 0.000024 0.000300 YES Maximum Displacement 0.000067 0.001800 YES RMS Displacement 0.000041 0.001200 YES
Hydrogen Cynide Molecule |
The optimisation file is linked to here
Vibrational Analysis
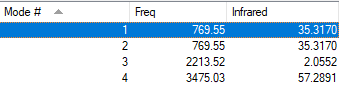
| Wavenum /cm-1 | Symmetry | Intensity /arbitrary units | Image |
| 770 | PI | 35 |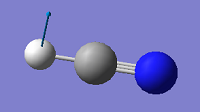 
|
| 770 | PI | 35 |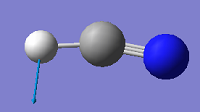 
|
| 2210 | SG | 2 | 
|
| 3475 | SG | 57 |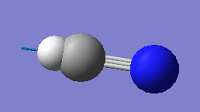 
|
Since HCN molecules are linear, 4 modes of vibration are expected using the 3N-5 rule. As shown in the table, there are two degenerate modes at 770 cm-1. There are 3 different vibrational energies and all of them have non-zero intensities. Therefore, 3 bands will be observed in an experimental spectrum of gaseous HCN.
The two degenerate modes at 770 cm-1 are two bending modes, in which the C-H bond bends in different directions. The vibrational mode at 2210 cm-1 is a symmetric stretching mode while the vibrational mode at 3475 cm-1 is an assymmetric stretching mode of higher energy.
Charge Analysis
Relative charge on the central C atom is +0.073, relative charge on the H atom is +0.234 and relative charge on the N atom is 0.308.
This is within my expectation because in HCN molecules, N atoms are much more electronegative than both C atoms and H atoms, hence N atom should be negatively charged and the other two atoms should be positively charged. The H atom is less electronegative than the C atom as there are more electron density surrounding the central C atom.
Molecular Orbitals
| Molecular Orbitals | Description |
|
It is the 1st molecular orbital of HCN. It is a bonding orbital that is occupied by two electrons. The 1s orbital from H and 2s orbitals from C and N contribute to form this orbital. This is a molecular orbital that is the the most core-like and it has an energy of -14.36054 au. As it is deep down in energy it does not produce large effects in bonding. |
|
It is the 6th molecular orbital of HCN. It is a non-bonding π orbital that is occupied by two electrons. The 2p orbitals from C and N contribute to form this orbital. This is a molecular orbital that is high in energy and it has an energy of -0.35935 au. It is also the highest occupied molecular orbital of the molecule, as the 7th molecular orbital and this orbital are degenerate. HOMO is the molecular orbital that attack other molecules in a reaction. The orbital lobes lie in the x-y plane. |
|
It is the 7th molecular orbital of HCN. It is a non-bonding π orbital that is occupied by two electrons. The 2p orbitals from C and N contribute to form this orbital. This is a molecular orbital that is high in energy and it has an energy of -0.35935 au. It is also the highest occupied molecular orbital of the molecule, as the 6th molecular orbital and this orbital are degenerate. HOMO is the molecular orbital that attack other molecules in a reaction. The orbital lobes lie in the x-z plane. |
|
It is the 8th molecular orbital of HCN. It is a π* orbital that is not occupied by any electrons. The 2p orbitals from C and N contribute to form this orbital. This is a molecular orbital that is higher than the ionization level and it has an energy of +0.01925 au. It is also the lowest unoccupied molecular orbital of the molecule. The 9th molecular orbital and this orbital are degenerate. LUMO is the molecular orbital that gets attacked by other molecules in a reaction. The orbital lobes lie in the x-y plane. |
|
It is the 9th molecular orbital of HCN. It is a π* orbital that is not occupied by any electrons. The 2p orbitals from C and N contribute to form this orbital. This is a molecular orbital that is higher than the ionization level and it has an energy of +0.01925 au. It is also the lowest unoccupied molecular orbital of the molecule. The 8th molecular orbital and this orbital are degenerate. LUMO is the molecular orbital that gets attacked by other molecules in a reaction. The orbital lobes lie in the x-z plane. |
ClF5 Molecules
Optimisation
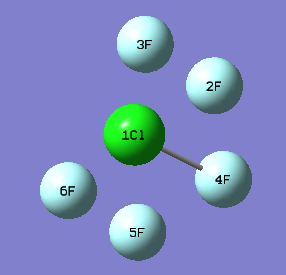
In ClF5 molecules, there are two chlorine environments, equitorial and axial. As shown in the image below, F2, F3, F5 and F6 are equitorial cholrine atoms, whil F4 is in an axial position.
Cl-F bond distance (equitorial) = 1.70Å
Cl-F bond distance (axial) = 1.65Å
F(equitorial)-Cl-F(equitorial) bond angle = 90°
F(equitorial)-Cl-F(axial) bond angle = 86°
| Calculation Method | RB3LYP |
| Basis Set | 6-31G(d,p) |
| E(RB3LYP) | -958.98366405 au |
| Point Group | C4V |
Item Value Threshold Converged? Maximum Force 0.000050 0.000450 YES RMS Force 0.000018 0.000300 YES Maximum Displacement 0.000134 0.001800 YES RMS Displacement 0.000055 0.001200 YES
Chlorine Pentafluoride Molecule |
The optimisation file is linked to here
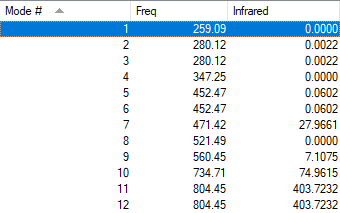
Vibrational Analysis
| Wavenum /cm-1 | Symmetry | Intensity /arbitrary units | Image |
| 259 | B2 | 0 | 
|
| 280 | E | 0 | 
|
| 280 | E | 0 | 
|
| 347 | B1 | 0 | 
|
| 452 | E | 0 | 
|
| 452 | E | 0 | 
|
| 471 | A1 | 28 |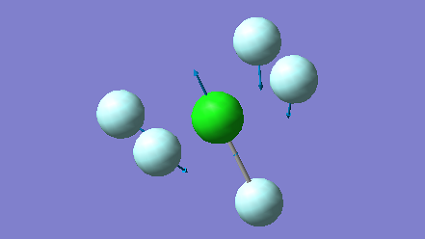 
|
| 521 | B2 | 0 |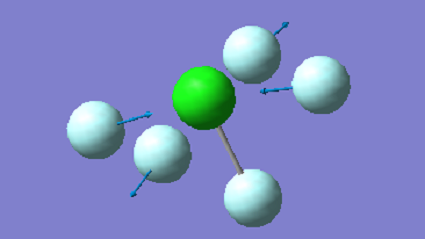 
|
| 560 | A1 | 7 |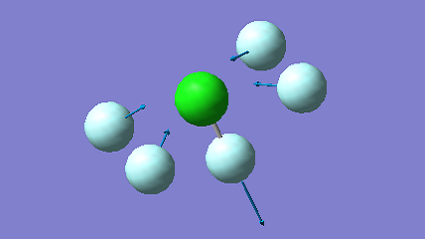 
|
| 735 | A1 | 75 |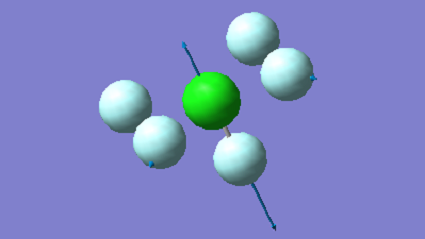 
|
| 804 | E | 404 | 
|
| 804 | E | 404 | 
|
Since ClF5 molecules are non-linear, 12 modes of vibration are expected using the 3N-6 rule. As shown in the table, there are two degenerate modes at 280 cm-1, two at 452 cm-1 and another two at 804 cm-1. There are only 9 modes of different energies. Among these 9 frequencies, vibrations at 259 cm-1, 280 cm-1, 347 cm-1, 452 cm-1 and 521 cm-1 have intensities of 0. Therefore, only 4 bands will be observed in an experimental spectrum of gaseous ClF5.
Charge Analysis
Relative charge on the central Cl atom is +1.998, relative charge on each equitorial F atom is -0.416 and relative charge on the axial F atom is -0.335.
This is within my expectation because in ClF5 molecules, F atoms are more electronegative than Cl atom, hence F atom should be negatively charged and Cl atoms should be positively charged. The axial F atom is less electronegative than the equitorial F atoms due to the lone pair of electrons at axial position.
Molecular Orbitals
| Molecular Orbitals | Description |
|
It is the 15th molecular orbital of ClF5. It is a bonding orbital that is occupied by two electrons. This is a molecular orbital that is really deep in energy and it has an energy of -1.18769 au. Compared to the 16th molecular orbital below, it is a lot lower in energy and more core-like. As it is deep down in energy it does not produce large effects in bonding. |
|
It is the 16th molecular orbital of ClF5. It is an anti-bonding orbital that is occupied by two electrons. This is a molecular orbital that is deep in energy and it has an energy of -0.93086 au. As it is deep down in energy it does not produce large effects in bonding. |
|
It is the 30th molecular orbital of ClF5. It is an anti-bonding orbital that is occupied by two electrons. 2p orbitals of F atoms and 3p orbital of the central chlorine atom contribute to this molecular orbital. This is the second highest molecular orbital and it has an energy of -0.37282 au. |
|
It is the highest occupied molecular orbital of ClF5. It is a bonding orbital that is high in energy and it is occupied by two electrons. 2p orbitals of F atoms and 3p orbital of the central chlorine atom contribute to this molecular orbital. The HOMO energy is -0.37282 au, which is a lot lower than that of LUMO because of the electrons it contains. Electrons in HOMO are the molecular orbitals that attack other molecules when ClF5 acts as a nucleophile in a reaction. |
|
It is the lowest unoccupied molecular orbital of ClF5. It is an anti-bonding orbital that is high in energy. 2p orbitals of F atoms and 3p orbital of the central chlorine atom contribute to this molecular orbital. The LUMO energy is -0.16331 au and it is the orbital that gets attacked when ClF5 acts as an electrophile. |
Marking
Note: All grades and comments are provisional and subject to change until your grades are officially returned via blackboard. Please do not contact anyone about anything to do with the marking of this lab until you have received your grade from blackboard.
Wiki structure and presentation 1/1
Is your wiki page clear and easy to follow, with consistent formatting?
YES
Do you effectively use tables, figures and subheadings to communicate your work?
YES
NH3 1/1
Have you completed the calculation and given a link to the file?
YES
Have you included summary and item tables in your wiki?
YES
Have you included a 3d jmol file or an image of the finished structure?
YES
Have you included the bond lengths and angles asked for?
YES
Have you included the “display vibrations” table?
YES
Have you added a table to your wiki listing the wavenumber and intensity of each vibration?
YES
Did you do the optional extra of adding images of the vibrations?
YES
Have you included answers to the questions about vibrations and charges in the lab script?
YES - All stretching vibrations are too low in intensity to be observed experimentally, so only two band are to be expected.
N2 and H2 0.5/0.5
Have you completed the calculations and included all relevant information? (summary, item table, structural information, jmol image, vibrations and charges)
YES
Crystal structure comparison 0.5/0.5
Have you included a link to a structure from the CCDC that includes a coordinated N2 or H2 molecule?
YES
Have you compared your optimised bond distance to the crystal structure bond distance?
YES
Haber-Bosch reaction energy calculation 1/1
Have you correctly calculated the energies asked for? ΔE=2*E(NH3)-[E(N2)+3*E(H2)]
YES
Have you reported your answers to the correct number of decimal places?
YES
Do your energies have the correct +/- sign?
YES
Have you answered the question, Identify which is more stable the gaseous reactants or the ammonia product?
YES
Your choice of small molecule 3/5
Have you completed the calculation and included all relevant information?
YES - this section was marked based on the calculation on HCN.
Have you added information about MOs and charges on atoms?
YES
The first displayed MO is a non-bonding MO rather than a bonding one because it does not interact with another AO at all. MOs 2 and 3 are bonding orbitals because the p orbitals overlap in phase.You missed to state the bonding/anti-bonding/non-bonding character of MOs 8 and 9. You could have been more specific labelling the relative orientations of contributing p orbitals. You could have explained and discussed the relative energies of the MOs.
Independence 1/1
If you have finished everything else and have spare time in the lab you could:
Check one of your results against the literature, or
Do an extra calculation on another small molecule, or
YES - This section was marked based on the calculation on ClF5.
The first displayed MO could have been labelled as non-bonding. You missed to mention the contributing AOs for the first two displayed MOs. You could have explained and discussed the relative energies of the MO
Do some deeper analysis on your results so far